Bizim bölümün tam karşısısna bir lokanta açılmış. Bana kalırsa kötü bir yer seçilmiş. Kaç kişi gider ki o lokantaya? Yakında batar. Batmadan gidelim dedik ailecek. Gittik de. Her masanın üstüne bir oyun koymuş lokanta sahibi. Herhalde çocukların oyuna dalıp, annelerini babalarını rahat bırakmları düşüncesiyle konmuş olacak. Güzel bir buluş. Kendimi bildim bileli oyuna düşkünümdür. Eşim de oyuna az düşkün değildir. Oyuncağı çocukların elinden alıp oynamaya başladık (“Yemekte oyun oynanmadığını bilmiyor musunuz?”). Çocukların sonradan söylediğine göre, biz oyuna dalmışken onlar da rahat rahat “makarna savaşı” yapmışlar.
“Yalnızların Oyunu” diye adlandırılan bu oyun, adından da anlaşılacağı gibi, tek kişilik bir oyun. Tahtadan bir üçgen üstüne $1 + 2 + 3 + 4 + 5$, yani $15$ tane, delik açılmış. Şöyle:

Ve bu deliklere girebilecek büyüklükte $14$ tane çubuk var. $14$ tane çubuğu deliklere yerleştireceksiniz(deliklerden biri boş kalacak demek ki). Örneğin şöyle (boş kalan deliği beyaz, çubuklu delikleri siyah olarak gösteriyorum):

Yapabileceğiniz bir tür yasal hamle var: çubuklardan birini yanındaki ya da çaprazındaki çubuğun üstünden aşırtıp bir sonraki deliğe sokabilirsiniz, ama bu hamleyi yapabilmemiz için çubuğun gireceği deliğin boş olması gerekir. Ve üstünden aşılan çubuk oyundan çıkartılır. Örneğin yukarıdaki durumda, en alt sıradaki soldan ikinci çubuğu, kuzey doğusundaki çubuğun üstünden aşırıp aşağıdaki durumu elde edebilirsiniz:

Bundan sonra, ikinci sıranın en sağındaki çubuğu solundaki çubuğun üstünden aşırtabilirsiniz:

Gitgide çubuk sayısı azalır. Amaç olabildiğince az çubuk bırakmak. Oyunun arkasında şöyle yazıyor:
Üç çubuk bırakan – eh! şöyle böyle – $10$ puan.
İki çubuk bırakan – ortalamanın üstünde – $25$ puan.
Bir çubuk bırakan – çok zeki – $50$ puan.
Bir çubuğu oyunun başındaki boş delikte bırakan – çok parlak – $100$ puan.
Hiçbri kımıldamayacak biçimde $8$ çubuk bırakan – dahi – $200$ puan.
Uzun süre “eh! şöyle böyle”ydik. Neden sonra “çok zeki” aşamasına geçebildik. Çok uğraşmamıza karşın “çok parlak” olamadık. Sıkıldık. “Dahi” aşamasını denedik. Baktık “dehalık” kolay değil, hileye baş vurduk. Başvurduğumuz hile, aslında matematikte sık kullanılan bir yöntemdir: kanıtlanacak teoreme sonradan başlanır. Yani kanıt sondan başa doğru bulunur. Örneğin, diyelim iki pozitif sayı için
$\sqrt{x^2+y^2} \leq \sqrt{x} + \sqrt{y} $
eşitsizliğini kanıtlamamız gerekiyor. Kanıtlamak istediğiniz bu eşitziliği karesini alırsanız,
$x + y \leq x + 2\sqrt{xy} + y$
bulursunuz. Sadeleştirince de bildiğimiz $0 \leq 2 \sqrt{xy}$ eşitsizliği bulunur. Kanıtı yazmak için yukarıdaki çıkarımları ters çevirmek gerekir: $0 \leq \sqrt{xy}$ eşitsizliğinden $0 \leq 2 \sqrt{xy}$ eşitsizliğini çıkarırız, bu eşitsizliğin soluna ve sağına $x + y$ ekleyerek, $x + y \leq x + y +2\sqrt{xy} $ buluruz. Bu son eşitsizliğin sağ tarafındaki terim $( \sqrt{x^2+y^2})^2 $ ye eşit. Şimdi iki tarafın karekökünü alarak, dilediğimiz eşitsizliği kanıtlamış oluruz”. İşte başvurduğumuz hile bu yöntemden esinlenmişti.
Oyuna sondan başladık. Oyunun sonudaki durumların ne olabileceğini bulduk önce. Sekiz tane çubuğu, hiçbiri kımıldamayacak biçimde nasıl yerleştirebilirdik? Kısa bir denemeden sonra (simetrileri saymazssak) iki çözümün olduğunu kolaylıkla anladık:

Çözümleri saptadıktan sonra, çözümlerin bir önceki hamlelerin ne olabileceklerine baktık. Örneğin, yukarıdaki birinci durma gelebilmek için, en alt sıranın soldan ya ikinci ya da dördüncü çubuğu oynanmıştır. Bu durumdan bir önceki durum şöyle olabilir:

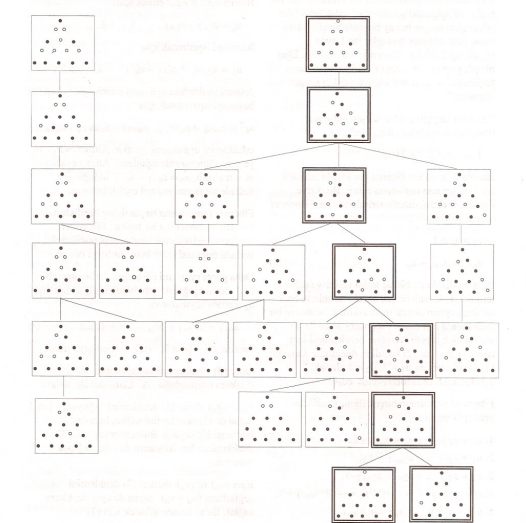
Sonra, teker teker daha önceki hamlelerimizin ne olabileceklerini saptadık. Yani geriye doğru gittik. Toplam $14$ çubuk var, demek ki $8$ çubuk bırakmak için geriye doğru $6$ hamle yapmamız gerekiyor. Oyunun tam bir şemasının çıkardık. Bir sonraki sayfada bu şemayı bulacaksınız. Bazan, geriye gidemedik, yani öyle bir duruma geldik ki, bir önceki hamle olamaz o durumda. O zaman durduk elbet. Ama bir önceki hamle -ya da hamleler- oldukça, geriye gitmeyi sürdürdük. Geriye doğru $6$ hamle yapabilmemiz gerekiyordu, yaptık da. Çift çerçeverli resimleri aşağıdan yukarıya doğru izleyerek “dahi” ünvanını elde ettik.
Bu “yalnızların oyunu” nu satıyormuş lokantacı. Aldık elbet. Hem de dört tane birden aldık. Herkese bir tane… Daha sonra sık sık gittik bu lokantaya. Her seferinde bir başka oyun vardı. Hepsinde de zeka ölçülüyordu: “Zehir gibisiniz!” “Böylesi görülmemiş!”, “Aşkolsun”, “Evrenin en zeki yaratığı!”, “Süper, ultra, extra, çok ama çok üstün zekâ!” Oyunlar da ucuz değil. Ama o kadar çok emek verdikten sonra almamak da olmuyor. Önceleri haftada bir gidiyorduk ailecek, sonra ben tek başıma kaçamaklar yapmaya başladım. Bölümün de tam karşısında olduğundan gitmesi kolay oluyor. Ne zaman hergün gitmeye başladığımı tam olarak anımsamıyorum. Birdenbire olmadı ki. Yavaş yavaş alıştım. Bizim bölümden hocalar, öğrenciler de orada yiyorlar öğlen yemeklerini. Hatta akşam ları aileleriyle gelenler de var. Yemek parasından başka, bir de oyuncak parası ödüyoruz…
Günlerden birgün, yine o lokontada “Dehaların dehası” olmaya çalışırken arka masadan bir konuşma kulağıma çarptı. Lokantanın sahibi bir arkadaşıyla konuşuyordu. Arkadaşı,
-Eee? İşler nasıl? diye sordu.
-Yuvarlanıp gidiyoruz işte… diye yanıtladı lokantacı.
-O kadar lokantacı iflas etti, sen nasıl dayanıyorsun şaşırıyorum…
-Yemekten pek kazanılmıyor doğrusu…
-Neden kazanıyorlar ya?
-Oyuncaklardan…
-Oyuncaklardan mı?
-Oyuncaklardan ya! Şu karşıdaki binayı görüyor musun? İşte orası matematik bölümü. Matematikçilere gururlarına okşayacak oyuncaklar sunuyorum. Sözümona zekâ ölçen oyuncaklar. Sen bu matematikçileri bilmezsin. Dayanamazlar bu tür oyuncaklara ve övgülere…
Kıssadan hisse: Para kazanmanın yolu bir değildir, kimi lokanta işleterek. Kimi de oyun oynatarak…