Yazar: Cihan Orhan (Ankara Üniversitesi, Matematik Bölümü, Öğretim Üyesi)
Yıl: 1995-1
Sayı: 21
Daha önceki bir yazımızda matematik-sevgi ilişkisini kurmaya çalışmış ve matematiğin resim, müzik mimari gibi bir güzel sanat olduğunu belirtmiştik. Bu nedenle bu yazımızı matematik-müzik ilişkisine ayırdık.
T. Pappas’ın “Yaşayan Matematik” isimli kitabının önsözünde şunlar yazılırdır: “Matematikten duyulan zevk bir şeyi ilk kez keşfetme deneyimine benzer. Çocuksu bir hayranlık ve şaşkınlık insanı sarar. Bu deneyimi bir kez yaşadıktan sonra, bu duyguyu unutamazsınız. Bu duygu, ilk kez mikroskopa bakıp da daha önce çevrenizde her zaman var olan ama göremediğiniz şeyleri gördüğünüz anki kadar heyecan vericidir.”
Gerçekten de matematiğin estetik çekiciliğine tamamen duyarsız, aydın bir insan bulmak biraz zordur. Matematiksel güzelliği tanımlamak çok güç olabilir fakat bu güçlük her tür güzellik konusunda geçerlidir.
Sadece düşüncede var olan olayların nerelerde uygulama alanı bulabileceği hiçbir zaman önceden tahmin edilemez. Bu nedenledir ki matematikçiler, yapılan çalışmaları estetik yönden değerlendirmekte, eserlerde bir sanatçı titizliği ile güzellik ve zerafet aramaktadırlar. İşte bunun için matematik-müzik ilişkisini bir magazin popüleritesi içinde sunmaya çalışacağız.
Orta çağda eğitim programlarında müzik, matematik ve astronomi ile aynı grupta yer alırdı. Matematik ve müzik ilişkisi, günümüzde bilgisayarlar aracılığı ile devam etmektedir.
Matematiğin müzik üzerindeki etkisini müzik parçalarının yanında görebiliriz. Bir müzik parçasında ritim (4:4 lük, 3:4 lük gibi), belirli bir ölçüye göre vuruş birlik, ikilik, dörtlük, sekizlik, onaltılık, … gibi notalar bulunur. Belirli bir ritimde, değişik uzunluktaki notalar, belirli bir ölçüye uydurulur. Her ölçünün ise değişik uzunluktaki notaları kullanan belirli sayıda vuruştan oluştuğu görülür.
Pisagor (M.Ö. 580-500) ve onun düşüncesini taşıyanlar sesin, çekilen telin uzunluğun bağlı olduğunu farkederek, müzikte armoni ile tamsayılar arasındaki ilişkiyi kurmuşlardır. Uzunlukları tamsayı oranlarında olan gergin tellerin de armonik sesler verdiği görülmüştür. Gerçekten de çekilen tellerin her armonik bileşimi tamsayıların oranı olarak gösterilebilir. Örneğin, do sesini çıkaran bir telin uzunluğunun 16/15’i si sesini verirken 6/5’i ise la sesini; 4/3’ü sol sesini; 3/2’si fa sesini; 8/5’i mi sesini; 16/9’u ise re sesini verir.
Görüldüğü gibi iki notayı bir arada duymak, iki frekansı ya da iki sayıyı ve bu iki sayı arasındaki oranı algılamaktan başka bir şey değildir. Demek ki armoni sorunu, iki sayının oranını seçme sorununa eşdeğerdir. Müzik, gizli bir aritmetik alıştırmasıdır diyen Leibniz’in haklılığı ortaya çıkıyor.
Müziği, belli kurallara uygun olarak oluşturulmuş basit birtakım seslerin birbirlerini izlemesinden oluşan cümleler topluluğu olarak tanımlayabiliriz. Bu kurallar, matematikte mantık kurallarına karşılık gelirler.
Bir çok müzik aletinin biçiminin matematiksel kavramlarla ilgili olduğunu belirtirsek şaşırmazsınız herhalde. Örneğin, aşağıdaki şekilde $x \leq 0$ için $y=2^x$ eğrisinin grafiği çizilmiş olup telli ya da üflemeli çalgıların biçimleri bu üstel eğrinin biçimine benzer.
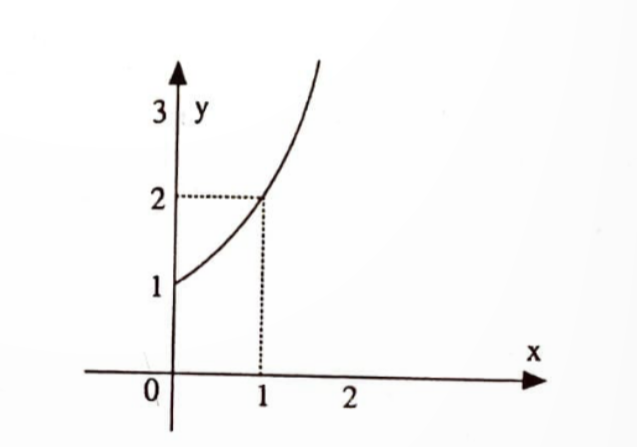
Müzikal seslerin niteliğinin incelenmesi 19. yüzyılda matematikçi J.Fourier tarafından yapılmıştır. Fourier, müzik aleti ve insandan çıkan bütün müzikal seslerin matematiksel ifadelerle tanımlanabileceğini ve bunun da periyodik sinüs fonksiyonları ile olabileceğini ispatlamıştır.
Birçok müzik aleti yapımcısı, yaptığı aletlerin periyodik ses grafini, bu aletler için ideal olan grafikle karşılaştırır. Yine elektronik müzik kayıtları da periyodik grafiklerle yakından ilişkilidir. Görüldüğü gibi bir müzik parçasının üretilmesinde matematikçilerle müzikçilerin birlikteliği çok önemlidir.
Matematik-müzik ilişkisinin bir başka özelliğini ortaya çıkarabilmek için matematikte ve mimaride çok sık kullanılan bir orandan söz etmek istiyorum.
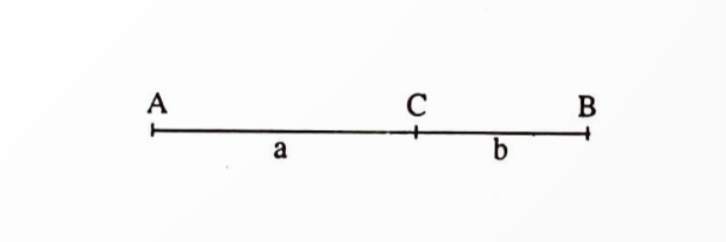
Uzunluğu $L$ olan bir $[A B]$ doğru parçasını ele alalım ve bunu uzunlukları $a$ ve $b$ olan iki parçaya ayıralım. Eğer $\frac{a}{b}=\frac{L}{a}$ yani, $\frac{a}{b}=\frac{a+b}{a}$ eşitliği gerçekleniyorsa, bu bölmeye $[A B]$ doğru parçasının altın bölümü adı verilir. $\frac{a}{b}$ oranına da ALTIN ORAN denir. Şimdi $x=a / b$ dersek, ilgili denklem $x^2-x-1=0$ şekline getirilebilir. Bu denklemin pozitif kökü $\frac{1+\sqrt{5}}{2} \cong 1.618$’dir.
Şimdi yeniden müziğe dönelim. İnsan kulağı için en uyumlu aralığın 8/5 frekans oranındaki major 6lı olduğu bilinmektedir. Bu oranın yukarıda bulduğumuz altın orana çok yakın bir oran olduğunu görüyoruz.
Bana göre müziğin matematikten farklı tarafı, bazı göz kamaştırıcı tuzaklar kullanarak, insanları büyüleyebilmesidir. Halbuki matematik bunu yapmaz. Russell bunu şöyle özetliyor: “İyi bakıldığı zaman matematik sadece doğruyu değil yüksek bir güzelliği de içerir. Matematik bu güzelliklere bürünmek için insan doğasındaki zayıflıklara başvurmaz; resim ve müziğin göz kamaştırıcı tuzaklarını da kullanmaz.”
Matematiğin müziğe kıyasla önemli tarafı şudur: Müzikal bir parçanın içerdiği estetik unsurun müzik eğitimi almayan kimseler tarafından anlaşılabilmesine karşılık, bir matematiksel teoride dinleyici veya okuyucunun tüm mantık zincirlerini izlemesi zorunluluğu vardır. Hatta içerdiği estetik unsuru da sezebilmesi gerekir.
Şüphesiz matematiğin de müzik gibi kompozitörleri ve virtüözleri vardır diyor hocamız Cahit Arf. Kompozitörler, teorileri kuranlar; virtüözler de teorileri gerçek manada anlayarak ifade edebilenler ve hissettirebilenlerdir.
Yazımızı, ünlü ressam Leonardo da Vinci’nin şu sözleri ile noktalamak istiyorum: “Matematiksel açıklamalar ve yöntemler kullanılmadan yapılan hiç bir araştırmaya bilimsel denemez.”
KAYNAKÇA
[1] C. Arf Matematiğin Şiir Yönü. Bilim ve Teknik; Şubat 1994.
[2] G.H. Hardy bir Matematikçinin Savunması. TÜBITAK yayınları, 1993.
[3] H.E. Huntly The Divine Proportion. Dover Publications, 1970.
[4] C. Orhan Matematik ve Sevi. Köy Hizmetleri Dergisi, sayı 48; 1993.
[5] T. Pappas Yaşayan Matematik. Sarmal Yayınevi, 1993.
[6] N. Tepedelenlioğlu Kim Korkar Matematikten. Sarmal Yayınevi, 1992.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Atahan Haznedar'a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

