Yazar: Ali Kemal Uncu (aku21@bath.ac.uk)
Yıl: 2022-4
Sayı: 114
Matematikte bir objeyi küçük parçalarına ayırmak ve bu objelerin analizini yapmak çok temel bir çözüm taktiğidir. Bu sebepten dolayı parçalanış kelimesi kendine matematiğin birçok alanında farklı (ancak benzer) anlam bulmuştur. Parçalanış teorisi doğal sayıların toplam işlemi altında kaç farklı şekilde oluşturulabileceğine, parçalanışlar arasındaki yapısal benzerliklere ve doğal sayı parçalanışlarının aritmetik ve asimptotik özelliklerine odaklanır. Parçalanış teorisi matematik içinde sayılar teorisi, kombinatorik, temsil teorisi, özel fonksiyonlar ve simetrik fonksiyonlar gibi birçok araştırma dalıyla etkileşim içindedir. Matematik dışında istatistiksel mekanik ve kuantum grupları başta olmak üzere, teorik fiziğin bazı alanlarında da kendini göstermiştir. Bilgisayar mühendisliği ve sembolik hesaplama alanında da tamsayı parçalanışları araştırmacıların çok karşılaştığı temel bir yapı taşıdır.
Toplamı $n$ olan, artmayan doğal sayıların sonlu bir listesine $n$ sayısının bir parçalanışı denir. Parçalanışların toplamsal yapısını vurgulamak için bu yazıda parçaların arasına toplam işareti koyacağız. İlk örnek olarak 4 sayısının tüm parçalanışlarını yazalım:
$$4,\quad 3+1,\quad 2+2,\quad 2+1+1,\quad 1+1+1+1.$$
Bir $n$ sayısının toplam parçalanış sayısını $p(n)$ ile gösterelim. Örneğimiz bize $p(4) =5$ olduğunu gösterir. Özel bir durum olarak boş (sıfır parçalı) listeyi, 0 sayısının tek parçalanışı olarak düşünürüz, yani $p(0)=1$’dir. Yakınında kâğıt kalem olan okurlar $p(1)=1$, $p(2)=2$, $p(3)=3$, $p(5)=7$, $p(6)=11$ ve $p(7)=15$ gibi birkaç özel durumu teyit edebilirler.
Bir araştırma alanı olarak parçalanış teorisinin adı oluşmadan önce de insanlar tamsayıların bazı özel parçalanışlarına yoğun bir ilgi göstermişlerdir. Ortaçağ matematikçileri üçgensel, kare ve beşgensel sayılar başta olmak üzere geometrik bir şekille özdeşleştirilebilen parçalanışlarla ilgilenmişlerdir. Bu şekilleri, temsil ettikleri parçalanışlarla birlikte kısaca hatırlatalım:
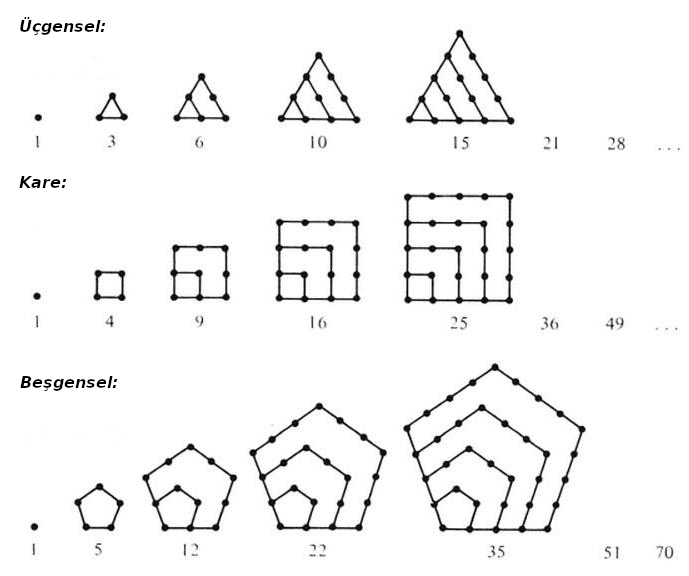
Sayılar teorisinin klasik zor sorularının bir kısmı parçalanış teorisiyle çok yakından ilişkilidir. Örneğin “hangi doğal sayılar, $x$ ve $y$ tamsayı olmak üzere, $x^2 + 2xy + 3y^2 – 2y$ şeklinde temsil edilebilir veya toplamda kaç farklı şekilde temsil edilebilir?” gibi birçok Diophantus denklemlerine parçalanış teorisi perspektifinden de bakılabilir. Benzer şekilde Milenyum sorularından Goldbach hipotezini ele alalım. Bu hipotez, ikiden büyük her çift sayının $p$ ve $q$ asal sayıları için $p+q$ şeklinde bir parçalanışı olduğunu ortaya atmaktadır.
Modern parçalanış teorisinin Philip Naudé’nin leonhard Euler’e 1740’ta attığı bir mektupla başladığını söyleyebiliriz. O mektupta Naudé, “50 sayısını 7 parçaya kaç farklı şekilde ayrıştırabiliriz?” diye sormuştur. Bu soru Euler’in 1751’de yazdığı De partitione numerorum (Sayıların parçalanışları hakkında) [2] adlı kitabının ilk kıvılcımları olmuştur. Parçalanışları tek tek yazarak Naudé’nin sorusuna cevap vermek hiç kolay değildir. Bu parçalanışları listelemeye yeltenecek olan okurlara 8946 parçalanışı yazarken bol bol sabır diliyoruz.
Genelde de tek tek parçalanışları listelemek ve özelliklerini kontrol etmek neredeyse imkânsızdır. Bundan dolayı parçalanışların sayısını bize bildirecek üreteç fonksiyonlarını kullanmayı tercih ederiz. Geleneksel sebeplerden dolayı burada degişken adı olarak $q$’yu kullanacağız. Bir $\{a_n\}_{n=0}^\infty$ dizisi için üreteç fonksiyonu $\sum_{n\geq 0} a_n q^n$ serisi olarak tanımlanır. Bu seride $q$ değişkeninin üstel değeri, dizi elemanının indeksini temsil etmektedir. Parçalanış sayısı üreteç fonksiyonunu ve serinin ilk birkaç terimini şöyle yazabiliriz: $$ \sum_{n \geq 0} p(n) q^n = 1+ q + 2 q^2 + 3q^3 + 5q^4 + 7q^5 + 11q^6+15q^7+\dots. $$
Bu üreteç fonksiyonunu daha iyi anlamak ve bu fonksiyona bir formül bulmak için geometrik serileri bilmek yeterlidir. Doğal sayı $a$ ve bir $q$ değişkeni için geometrik seriler, $$ \frac{1}{1-q^a} = 1+q^a + q^{2a} + q^{3a} + q^{4a} + q^{5a} + \dots $$ şeklinde tanımlanır. Yukarıda verilen geometrik serinin sağ tarafındaki $q$-kuvvetlerini bir kez de toplamsal olarak yazalım: $$ = 1+q^a + q^{a+a} + q^{a+a+a}+q^{a+a+a+a} + q^{a+a+a+a+a}+\dots. $$ Bu listede her $q$ terimi üstel değeri olarak parçaları $a$ doğal sayısı olan bir parçalanış taşır. Geometrik serilerin bu yorumlanışı bize $1/(1-q^a)$ rasyonel fonksiyonunun parçaları $a$ boyutunda olan parçalanışların sayısının üreteç fonksiyonu olduğunu gösterir. Bu fikri tüm doğal sayı alt kümelerine genellemek de çok kolaydır. $\mathcal{A}$ doğal sayıların bir alt kümesi olsun. Parçaları $\mathcal{A}$ kümesinden olan parçalanış sayılarının üreteç fonksiyonu geometrik serilerin bir çarpımı olarak yazılır ve şu şekildedir: \begin{equation}\prod_{a\in\mathcal{A}}\frac{1}{1-q^a}. \tag{1} \end{equation} Bu çarpım geometrik serilere bakıldığında $\mathcal{A}$ kümesindeki elemanların olası her türlü kombinasyonunu (yani bu kümenin elemanlarıyla oluşturulabilecek her parçalanışı) içerir. Benzer şekilde, parçaları $\mathcal{B}$ kümesinden olan ve hiçbir parçası kendini tekrarlamayan parçalanışların üreteç fonksiyonu da bir biçimsel çarpım olarak, \begin{equation}\prod_{b\in\mathcal{B}}(1+q^b) \tag{2}\end{equation} şeklindedir.
Şimdiden Euler’in 1751’de sunduğu bir teoremini hem anlayabilecek hem de ispatlayabilecek kadar bilgiye sahip olduk.
Teorem 1 (Euler’in Parçalanış Özdeşliği).
Her $n$ doğal sayısı için, o sayının parçaları tekrarlanmayan parçalanışlarının sayısı, aynı $n$ sayısının sadece tek parçalar kullanılarak üretilen parçalanışlarının sayısına eşittir.
Bu tip “her doğal sayı için $\mathcal{A}$ kümesinin özelliklerini sağlayan parçalanışların sayısı $\mathcal{B}$ kümesinin özelliklerini sağlayan parçalanışların sayısına eşittir” formatındaki bağıntılara parçalanış özdeşlikleri denir. Euler’in özdeşliğini ispatlamadan önce, teoremde bahsi geçen parçalanış kümelerine $n=6$ özel durumunda bakalım. Parçaları tekrarlanmayan, toplamı 6 olan parçalanışları bir küme olarak şöyledir: \[\{6,\ 5+1,\ 4+2,\ 3+2+1\}.\] Parçalanışları sadece tek sayılardan oluşanlar da şu şekilde yazılır, \[\{5+1,\ 3+3,\ 3+1+1+1,\ 1+1+1+1+1+1\}.\] Bu iki kümenin birbirinin aynı olmadığı aşikârdır; ancak özdeşliğin de dediği gibi iki kümenin de eleman sayısı aynıdır.
İlk bakışta bu farklı parçalanışlar arasında teoremi ispatlayacak birebir ve örten bir bağıntı bulmak mümkün olmayabilir. Bu parçalanış özdeşlikleri için bir ortak özelliktir. Genelde bu teoremlerin ispatları, teoremlerde bahsi geçen parçalanışların sayı dizileri için oluşturulan üreteç fonksiyonlarının eşit olduğunu gösterme yoluyla yapılır. Euler’in özdeşliğini ispatlamak için de öncelikle teoremle alakalı olan üreteç fonksiyonlarına bakalım. Parçaları tekrarlamayan parçalanışların sayısını veren üreteç fonksiyonu ($(2)$’de $\mathcal{B}=\{1,2,3,\dots\}$ alarak) $\prod_{i=1}^\infty (1~+~q^i)$’dir. Tek parçalardan oluşan parçalanışların sayısını veren üreteç fonksiyonu da ($(1)$’de $\mathcal{A}=\{1,3,5,\dots,(2i~-~1),\dots\}$ seçerek) $\prod_{i=1}^{\infty}(1-q^{2i-1})^{-1}$ şeklinde yazılır. Bu iki fonksiyonun (biçimsel çarpımlar anlamında) eşit olduğunu göstermek için asağıdaki adımları takip etmek yeterlidir:
$$\begin{align} \prod_{i=1}^\infty (1+q^i) &= \prod_{i=1}^\infty (1+q^i)\frac{(1-q^i)}{(1-q^i)}\\ &= \prod_{i=1}^\infty \frac{(1-q^{2i})}{(1-q^i)} = \prod_{i=1}^\infty(1-q^{2i})\prod_{i=1}^\infty \frac{1}{(1-q^{i})}\\ &= \prod_{i=1}^\infty(1-q^{2i})\prod_{i=1}^\infty \frac{1}{(1-q^{2i-1})(1-q^{2i})}\\ &= \prod_{i=1}^\infty\frac{1}{(1-q^{2i-1})}\frac{(1-q^{2i})}{(1-q^{2i})} = \prod_{i=1}^{\infty}\frac{1}{(1-q^{2i-1})}. \end{align}$$
Üreteç fonksiyonlarının eşit oluşu bu iki parçalanış kümelerinin saydığı elemanların sayılarının da aynı olduğunu ispatlar.
Üreteç fonksiyonları, parçalanış teorisinde oluşan kombinatorik sorularını, analitik eşitliklere bağlar. Bu bağlantı kombinatorik sorularına analitik yönden, analitik sorulara kombinatorik yönden bakabilmemizi sağlar ve teoriyi zenginleştirir. (Analiz severlerin yakınsaklık kaygıları hiç olmasın, bu üreteç fonksiyonlarının hepsi $|q|<1$ olduğu sürece mutlak yakınsaktır.)
Euler’in teoreminden belki de daha ünlü olan Rogers-Ramanujan parçalanış özdeşlikleri şu şekildedir:
Teorem 2 (Rogers–Ramanujan Parçalanış Özdeşlikleri).
$j=0$ veya $j=1$ olmak üzere, her $n$ doğal sayısı için, $n$ sayısının en küçük parçası $j$’den büyük olan ve parçaları arasında en azından 2 fark olan parçalanışlarının sayısı, aynı $n$ sayısının 5’e bölündüğünde $1+j$ veya $4-j$ kalanını veren parçalar kullanılarak üretilen parçalanışlarının sayısına eşittir.
Örneğin $j=0$ ve $n=9$ durumu için parçaları arasında en az 2 fark bulunan parçalanışların kümesi, \[\{9,\ 8+1,\ 7+2,\ 6+3,\ 5+3+1\}\] şeklindedir. Öte yandan 9’un 5’e bölümünde $1$ veya $4$ kalanını veren parçalardan oluşan parçalanışların kümesi şöyledir:
$$ \{9,\ 6+1+1+1,\ 4+4+1,\ 4+1+1+1+1+1,\ 1+1+1+1+1+1+1+1+1 \} $$
İki kümede de 5 eleman bulunmasına rağmen, Euler’in parçalanış özdeşliğinde olduğu gibi, bu kümeler birbirinden farklı parçalanışlara sahiptir.
Rogers–Ramanujan teoremin üreteç fonksiyonu versiyonunu da hemen sunalım.
Teorem 3 (Rogers–Ramanujan Özdeşlikleri).
$j=0$ veya $j=1$ olmak üzere, \begin{equation}\label{RRanalytic}\sum_{n\geq 0} \frac{q^{n^2+jn}}{\prod_{i=1}^n(1-q^i)} = \prod_{i=0}^\infty\frac{1}{(1-q^{1+j+5i})(1-q^{4-j+5i})}. \tag{3}\end{equation}
Analitik versiyonuna bakıldığında Rogers-Ramanujan teoremi tamamen çarpımlarına ayrılabilen iki tane sonsuz seri örneğini barındırır. Bu teoremin ispatı özel fonksiyonlar teorisinden, özellikle $q$-(hipergeometrik) serilerinden, yardım gerektirir. İspatı burada yapmayacak olsakta, bize Rogers–Ramanujan teoreminin ispatında ve birçok yerde yardımcı olan bir teoremi burada paylaşmakta yarar var.
Teorem 4 (Jacobi Üçlü Çarpım Formülü).
$x$ ve $q$ değişkenler olmak üzere,
\begin{equation}\sum_{i=-\infty}^\infty x^{2i} q^{i^2} = \prod_{i=1}^\infty (1-q^{2i})(1+q^{2i-1}x^2)(1+q^{2i-1}x^{-2}). \tag{4}\end{equation}
Özel fonksiyonlarla parçalanış teorisinin birbirini destekleyen bir ortaklığı vardır. Üreteç fonksiyonlarının kullanıldığı ispatlarda $q$-hipergeometrik serilerinin bilinen özelliklerine ihtiyaç duyulur. Birçok $q$-serisi eşitliği de parçalanış teorisinde yapılan gözlemlerle ortaya çıkmış ve ispatlanmıştır.
Jacobi üçlü çarpım formülü parçalanış teorisinde sorulabilecek bazı direkt sayma sorularının cevaplanmasında da bize yardımcı olabilen bir denklemdir. Mesela bu yazının başlarında hangi doğal sayıların $x^2+2xy+3y^2-2y$ şeklinde yazılabileceğini ve kaç farklı şekilde yazılabileceklerini sormuştuk. Bir $n$ tamsayısı için bu sayının $x^2+2xy+3y^2-2y$ şeklindeki birbirinden farklı gösterimlerinin sayısı $t(n)$ olsun. Bu gösterimlerin üreteç fonksiyonlarını şimdi Jacobi üçlü çarpımı yardımıyla çarpımsal bir formatta bulabiliriz. Tamsayılar üzerinde $n,\ x,$ ve $y$ değişirken $x^2+2xy+3y^2-2y = n$ Diophantus denkleminin tüm çözümlerinin üreteç fonksiyonunu sonsuz toplam olarak yazabiliriz:
\begin{equation}\sum_{n=-\infty}^\infty t(n) q^n = \sum_{x,y=-\infty}^\infty q^{x^2+2xy+3y^2-2y}. \tag{5}\end{equation} Bu sonsuz toplamda sabit bir $n$ tamsayısı için $x^2+2xy+3y^2-2y = n$ denklemini çözen her $(x,y)$ çifti $q^n$ teriminin katsayısına 1 ekler. Böylece $x^2+2xy+3y^2-2y = n$ denkleminin total çözüm sayısı olan $t(n)$, $x$ ve $y$ tüm tamsayılar üzerinde gezerken ortaya çıkmış olur.
Değişken değişimiyle $(5)$’in sağındaki iki değişkenli iç içe olan toplamı iki bağımsız seri haline getirebiliriz. Bunun için $x=z-y$ değişken değişimini yapalım. Böylece $x^2+2xy+3y^2-2y$ polinomu $z^2+ 2y^2-2y$’ye dönüşür ve $(x,y)$ için iç içe olarak yazılması zorunlu olan bu toplam, $2xy$ çarpraz terimi ortadan kalktığından, $(z,y)$ için iki ayrık toplam olarak bağımsız şekilde yazılabilir. Bu şekilde elimize Jacobi üçlü toplamını kullanabileceğimiz iki tane toplam çıkar. Bu toplamlar ve bu toplamlara $(4)$ sayesinde eşit olduğunu gördüğümüz sonsuz çarpımlar şu şekildedir:
$$\begin{align}\nonumber \sum_{x,y=-\infty}^\infty q^{x^2+2xy+3y^2-2y} &= \left(\sum_{z=-\infty}^\infty q^{z^2}\right)\left(\sum_{y=-\infty}^\infty q^{2y^2 – 2y}\right)\\ &= \left(\prod_{i=1}^{\infty} (1-q^{2i})(1+q^{2i-1})^2\right)\!\times\!\left(\prod_{i=1}^{\infty} (1-q^{4i})(1+q^{4i-4})(1+q^{4i})\right)\\ &= \prod_{i=1}^{\infty}\hspace{-1px} (1\hspace{-1px}-\hspace{-1px}q^{2i})(1\hspace{-1px}+\hspace{-1px}q^{2i-1})^2(1\hspace{-1px}-\hspace{-1px}q^{4i})(1\hspace{-1px}+\hspace{-1px}q^{4i-4})(1\hspace{-1px}+\hspace{-1px}q^{4i}).\end{align}$$
Küçük $i$ değerleri için ilk birkaç terimi bu çarpımı daha iyi tanımak adına yazalım:
$$\begin{align}
\prod_{i=1}^{\infty} &\hspace{-1px} (1\hspace{-1px}-\hspace{-1px}q^{2i})(1\hspace{-1px}+\hspace{-1px}q^{2i-1})^2(1\hspace{-1px}-\hspace{-1px}q^{4i})(1\hspace{-1px}+\hspace{-1px}q^{4i-4})(1\hspace{-1px}+\hspace{-1px}q^{4i})\\ &=2 (1+q)^2 (1-q^2) (1+q^3)^2 (1-q^4)^2(1+q^4)\dots. \tag{6}\end{align}$$
Bulduğumuz çarpımsal gösterim $t(n)$ sayılarını kolayca bulmamızı da sağlar. Mesela, $x$ ve $y$ tamsayıları için, $x^2+2xy+3y^2-2y = 0$ denklemini çözmek kolay olmayabilir. Öte yandan eğer amacımız $x^2+2xy+3y^2-2y = 0$ denklemini sağlayan $(x,y)$ çiftlerini bulmak değil de toplamda bu denklemin kaç çözümü olduğunu bulmaksa, bunu $(6)$’da $q^0$ terimininin katsayısına bakarak bulabiliriz. Cabası, bu yaklaşım, $t(n)$ sayılarını hesaplamayı hem elle hesap için hem bilgisayarla hesaplamalar için çok daha kolaylaştırır. Bulduğumuz $(6)$ çarpımında $q^0$ terimini sadece her terimdeki sabit terimleri çarparak elde edebiliriz. Bu da $t(0)=2$ olduğunu bize gösterir. Aynı şekilde eğer $k$ negatif bir tamsayı ise $t(k)=0$ olduğunu, $t(1)=4$, $t(2)=t(3)=0$, $t(4)=6$ ve bunun gibi değerleri çok çaba sarf etmeden hesaplayabiliriz.
Burada oluşturduğumuz üreteç fonksiyonu $(5)$’in literatürdeki adı bu kuadratik formun theta serisidir. Modüler formlar ve simetrik fonksiyonları önceden biraz okumuş olanlar bu isme eminiz ki aşinalardır. Benzer olarak, Rogers–Ramanujan teoreminin üreteç fonksiyonlarından $(3)$’ün sağ tarafında gördüğümüz çarpımda modüler fonksiyonlarla yakından alakalıdır. Her modüler fonksiyon gibi parçalanış sayısı üreteç fonksiyonu da fonksiyonel olarak birçok simetriyi içinde saklar. Bu tip simetri özellikleri parçalanışların da aritmetik özelliklerini görmemizi sağlar. Bu simetrilerin bize gösterdiği belki de en güzel özellik Ramanujan denklikleridir.
Teorem 5 (Ramanujan denklikleri).
Her $n = 0,1,2,\dots$ için, $$\begin{align} p(5n+4)&\equiv 0\pmod{5},\\ p(7n+5)&\equiv 0\pmod{7},\\ p(11n+6)&\equiv 0\pmod{11} \end{align}$$ denklikleri gerçeklenir.
Bu denkliklerin ilki, $5n+4$ şeklinde yazılabilen sayıların parçalanış sayılarının 5’e bölünebildiğini söyler. Ramanujan bu denklik gözlemlerini MacMahon’un yapmış olduğu ilk 200 sayının parçalanış sayıları listesine bakarken yapmıştır. Bu teoremin ispatıysa üreteç fonksiyonlarının simetrilerini çalışmamızı ve bu üreteç fonksiyonlarını, \begin{equation}\sum_{i\geq 0} p(5i+4) q^i = 5\prod_{i=1}^\infty\frac{(1-q^{5i})^5}{(1-q^i)^6}\tag{7}\end{equation} gibi çok özel şekillerde yeniden yazmamızı gerektirir. Bu tip özel gösterimleri bulmak ve ispatlamak modüler formların simetrilerini kullanarak mümkündür.
Böyle özel gösterimlerin bulunmasından sonra denkliklerin ispatı rutin bir sayılar teorisi argümanına dönüşür: $(7)$ denkleminin sağ tarafındaki sonsuz çarpımın (geometrik serileri hatırlayarak) katsayıları tamsayılar olan bir sonsuz seri olarak yazılabileceğini biliyoruz. Bu bilgiyle beraber, sonsuz çarpımın önünde bulunan 5 katsayısı bize $(7)$’nin sağındaki terimin seri açılımındaki her katsayısının 5’in bir katı olacağını gösterir. $(7)$ eşitliği bulduğumuz özelliği diğer tarafa transfer etmemizi sağlar, yani soldaki serinin her katsayısının 5’in bir katsayısı olacağını söyler.Bu şekilde $p(5n+4)\equiv 0\pmod{5}$ olduğunu ispatlamış oluruz.
Gördüğümüz küçük örnekler çok belli etmese de parçalanış sayıları çok hızlı bir biçimde artar. Bunu 10’un birkaç kuvvetiyle gözler önüne serelim:
$$\begin{align} p(1)&=1\\ p(10)&=42\\ p(100)&=190.569.292\\ p(1000)&= 24.061.467.864.032.622.473.692.149.727.991\\ &\ \, \vdots \end{align}$$
Dahası bu sayıları direkt olarak kolayca hesaplamamızı sağlayan bir formül de yok. $P(q) = \sum_{i\geq 0} p(i) q^i$, ve $C$ birim çember içinde kompleks orijininin etrafında saatin aksi yönünde dönen bir kontür olsun. Cauchy integral formülü ile $p(n)$ sayısını izole edebiliriz: \[p(n) = \frac{1}{2\pi i} \oint_C \frac{P(z)}{z^{n+1}}dz.\]
Hardy ve Ramanujan bu integralin ve $C$ kontürünün özelliklerini kullanarak $p(n)$ için bir asimptotik formül vermişlerdir. Bu formül daha sonra Rademacher tarafından mükemmelleştirilmiştir. Asimptotik olarak $n\rightarrow\infty$ limitinde, \[p(n) \sim \frac{1}{4n\sqrt{3}}e^{\pi\sqrt{2n/3}}\] şeklinde bir benzerlik görülmektedir. Yani parçalanış sayısı ilişkinin sağındaki üstel fonksiyon hızında büyümektedir.
Burada bahsedilen 3 temel alan olan parçalanış özdeşlikleri, parçalanış denklikleri ve parçalanış sayılarının büyüme hızının anlaşılması hâlâ çok aktif araştırma alanlarıdır. Birçok sorunun kesişim noktası olmasıyla, parçalanış teorisine her gün yeni teknikler ve bu konuya ilgi geliştiren yeni araştırmacılar eklenmektedir. Bu yazıda sunulan sonuçlar ve bu teoride yer alan diğer temel fikirler Andrews’un 1976 senesinde kaleme aldığı The Theory of Partitions (Parçalanışlar teorisi) adlı matematik ansiklopedisinde bulunabilir [1]. Son 50 senede ortaya çıkan yeni teknikler ve bulgular artık parçalanış teorisi konulu ikinci bir ansiklopedinin yazılmasının gerekliliğini de ortaya koymaktadır. Özellikle yaklaşık son 10 yılda, deneysel olarak bilgisayar yardımıyla bulunmuş birçok nefes kesici hipotez ortaya çıkmıştır. Bu soruların birçoğu hâlâ birilerinin onları ispatlamasını beklemektedir.
Bu temel ve öğrenmesi çok zevkli matematik konusunu gelecek nesillerle tanıştırmak tabii ki çok önemli. Bu sebeple Sabancı Üniversitesi’nden Kağan Kurşungöz ve Gebze Teknik Üniversitesi’nden Zafeirakis Zafeirakopoulos ile Türkiye içinde çalıştaylar organize etmeye ve yeni fikirler üzerinde bizimle araştırma yapacak gençlerle tanışmaya çalışıyoruz. Parçalanış teorisi klasik bir üniversite müfredatında bulunmasa da bu konuya dünyada ilginin arttığını da görmekteyiz. 2018’de Nesin Matematik Köyü’nde ilk parçalanış teorisi çalıştayını 5 farklı ülkeden toplam 15 katılımcıyla gerçekleştirdik [3]. Katılımcılarımızdan, matematik eğitimine devam etmeye karar verenlerin ve doktora tezlerini parçalanış teorisiyle ilgili konularda yapmayı seçenlerin olması çok mutlu ediciydi. İkinci parçalanış teorisi çalışmamızda bu sayılar 8 ülkeden 18 kişiye yükseldi [4]. Haziran 2022’nin başında yine Nesin Matematik Köyü’nde, bu sefer Türk Matematik Derneği’nin de desteğiyle, gerçekleştirdiğimiz çalıştayda katılımcılarımızla ortaklaşa bazı bilimsel çalışmaların temellerini attık.
Çalıştayları organize ederken ilk amacımız matematik alanında yeni araştırmacılarla ve bu konuda doktoralarını yapan ya da yapmayı isteyen öğrencilerle etkileşime geçmekti. Kendi adıma ben bu amaca her toplantımızda ulaştığımıza inanıyorum. İlk çalıştayımızdaki bir öğrencimiz, ikinci çalıştaya meslektaşımız olarak katıldı. Bundan daha güzel bir geri dönüş nasıl olabilir? İkinci çalıştayımızda bizimle orada bulunan her araştırmacı çalıştığı konuları ve teknikleri grupla paylaştı ve üzerinde beraber çalışabileceğimiz sorular havalarda uçuştu. Yeni arkadaşlıklar kuruldu. Yeni fikirler tartışıldı. Yeni iş ve araştırma bağlantılarının temelleri atıldı. Matematiğe yapacağı pozitif etkilerini görmeyi sabırsızlıkla beklediğim bir hafta geçirmiş olduk.


Gönüllü olarak organize ettiğimiz bu çalıştaylara gelen pozitif yorumlar her türlü yorgunluğumuzu unutturuyor. Aramızda bir sonraki buluşma ne zaman olmalı diye konuşmaların başlamasına vesile oluyor. Gelecek toplanmamızda umarım ki sizinle de tanışırız. O zamana kadar, ikinci çalıştayda verdiğimiz bütün dersleri [4] adresinden ve Nesin Matematik Köyü’nün YouTube sayfasından izleyebilirsiniz.
Kaynaklar
[1] G. E. Andrews, The theory of partitions, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1998. Reprint of the 1976 original. MR1634067 (99c:11126).
[2] L. Euler, De partitione numerorum, Novi Commentarii academiae scientiarum Petropolitanae $3(1750 / 51)$ 1753, p. 125-169, reprinted in Opera Omnia Series I vol 2 p. 254-294. Available through The Euler Archive at, www.EulerArchive.org.
[3] A. K. Uncu, Workshop on Integer Partitions https://akuncu.com/2018/05/28/workshop-on-integer-partitions/.
[4] A. K. Uncu, Second Workshop on Integer Partitions https://akuncu.com/2022/06/10/second-workshop-on-integer-partitions/.

