Yazar: Mehmet Tagiyev & Belgin Mazlumoğlu (Mimar Sinan Üniversitesi Matematik Bölümü öğretim üyeleri)
Yıl: 1994
Sayı: 5
Bana bir destek noktası verin; dünyayı yerinden oynatayım.
Arşimet
M.Ö. 3. yüzyılda yaşamış olan Arşimet, mekaniğin sade ve açık bir kavramı olan ağırlık merkezini geometri problemlerinin çözümünde ustalıkla kullanmıştır. Bu yazımızda Arşimet’in metodu nasıl kullandığını inceleyeceğiz.
Ağırlık merkezi kavramını ve onun özelliklerinin ciddi matematiksel tanımlarını vermeden önce, ağırlık merkezinin sezgisel olarak açık olan manasını anlatalım.
Aşağıda, tamamen mekanik düşüncelerden doğan maddesel nokta, maddesel noktalar sistemi, kütle, v.s., gibi terimleri kullanacağız. Maddesel nokta denilince anlaşılması gereken, kütlesi çok küçük hacimde toplanmış cisim olmalıdır; veya kütle ile teçhiz edilmiş geometrik bir nokta anlaşılmalıdır. Eğer $A$ noktası bir $m$ kütlesi ile teçhiz edilmişse, bunu $(m, A)$ veya $m A$ şeklinde göstereceğiz. $A_{1}, A_{2}, \ldots, A_{n}$ noktalar sistemi sırasıyla $m_{1}, m_{2}, \ldots, m_{n}$ kütleleriyle teçhiz olunmuşsa bunu $\left(m_{1} A_{1}, m_{2} A_{2}, \ldots, m_{n} A_{n}\right)$ şeklinde göstereceğiz.
Kütleleri $m_{1}$ ve $m_{2}$ olan iki küçük $K_{1}$ ve $K_{2}$ kürelerini gözönüne alalım ve onların kütlesiz sert bir çubuk vasıtasıyla birleştirildiklerini farzedelim. O zaman bu çubuğun üzerinde öyle bir $G$ noktası vardır ki, çubuk bu noktadan asıldığında küreler dengede kalır (Şekil 1). $G$’nin bu sistemin ağırlık merkezi olduğunu mekanikten biliyoruz.
Şimdi kütleleri $m_{1}$, $m_{2}$, $m_{3}$ olan ve doğrusal olmayan $K_{1}$, $K_{2}$, $K_{3}$ kürelerinin kütlesiz sert çubuklar yardımıyla (Şekil 2) birleştirildiğini farzedelim. Bu durumda $K_{1} K_{2} K_{3}$ üçgeninde öyle bir $G$ noktası vardır ki sistem bu noktadan asıldığında dengede kalır. $K_{1} K_{2} K_{3}$ üçgeninin bu özel noktasına $\left(m_{1} K_{1}, m_{2} K_{2}, m_{3} K_{3}\right)$ sisteminin ağırlık merkezi denir.
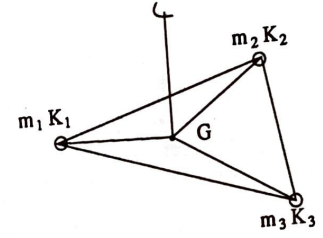
Maddesel noktaları herhangi bir sayıda alıp, oluşan sistemin ağırlık merkezini bulmak mümkündür. Şimdilik $\left(m_{1} K_{1}, m_{2} K_{2}, m_{3} K_{3}\right)$ sistemiyle yetinelim ve ağırlık merkezinin sezgisel olarak açık olan aşağıdaki özelliklerini kabul edelim:
(G1) Herhangi $\left(m_{1} K_{1}, m_{2} K_{2}, m_{3} K_{3}\right)$ sisteminin tek bir ağırlık merkezi vardır.
(G2) $\left(m_{1} K_{1}, m_{2} K_{2}\right)$ sisteminin ağırlık merkezi $G$, bu noktaları birleştiren doğru parçasının üzerindedir ve bu noktanın yeri Arşimet’in ünlü “kol kuralı” ile bulunabilir $$ m_{1} d_{1}=m_{2} d_{2} $$
(G3) Eğer $\left(m_{1} K_{1}, m_{2} K_{2}, m_{3} K_{3}\right)$ sisteminde herhangi iki noktayı (örneğin $m_{1} K_{1}$, $m_{2} K_{2}$ noktalarını) ayırıp onların ağırlık merkezi olan $G_{1}$ noktasına $m_{1}+m_{2}$ kütlesini yerleştirirsek, yani $\left(m_{1} K_{1}, m_{2} K_{2}\right)$ altsistemi yerine $\left((m_1+m_2) G_{1}\right)$ sistemini yazarsak, şimdi elde ettiğimiz $\left(\left(m_{1}+m_{2}\right) G_{1}, m_{3} K_{3}\right)$ sisteminin ağırlık merkezi ile $\left(m_{1} K_{1}, m_{2} K_{2}, m_{3} K_{3}\right)$ sisteminin ağırlık merkezi aynıdır.
Teori bu kadar. Şimdi mekaniğin basit ve açık gerçeklerinden kaynaklanan bu teori ile aşağıdaki geometri problemlerini çözelim. İlk önce bir üçgenin kenarortaylarının özelliklerini bulalım.
Teorem 1. (Arşimet, M.Ö. 3. yy) Herhangi bir üçgenin üç kenarortayı bir noktada kesişirler ve kesişme noktasında 2:1 oranında bölünürler.
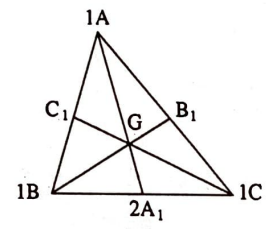
Kanıt. $\quad$ $A B C$ üçgeninin $A$, $B$, $C$ tepe noktalarına 1’er birim kütle yerleştirelim. (G1) özelliğine göre $(1 A, 1 B, 1 C)$ sisteminin tek bir $G$ ağırlık merkezi vardır. (G3) özelliğine göre $(1 B, 1 C)$ sisteminin toplam kütlesini onların ağırlık merkezine yerleştirirsek tüm sistemin ağırlık merkezi değişmez. $B$ ve $C$ noktalarının kütlesi aynı olduğundan (G2)’ye göre onların ağırlık merkezi $B C$’nin orta noktası olacaktır:
$$ 1 \times\left|B A_{1}\right|=1 \times\left|A_{1} C\right| \quad \text { (kol kuralı). }$$
$A1$ noktasına $B$ ve $C$ noktalarının toplam kütlesi olan $1+1=2$ birim kütleyi yerleştirerek $\left(1 A, 2 A_{1}\right)$ sistemine bakalım. O zaman $\left(1 A, 2 A_{1}\right)$ sisteminin ağırlık merkezi ile $\left(1 A_{1}, 1 B, 1 C\right)$ sisteminin ağırlık merkezi aynı olacaktır. $(1 A, 2 B)$ sisteminin ağırlık merkezi $A A_{1}$ doğru parçası üzerindedir ve gene kol kuralını kullanarak
$$1 \times|A G|=2 \times\left|G A_{1}\right|$$
ve buradan da
$$|A G|:\left|G A_{1}\right|=2: 1$$
buluruz.
Benzer olarak, $1 A$ ve $1 B$ noktalarının ağırlık merkezi $2 C_{1}$ noktasıdır ve $\left(2 C_{1}, 1 C\right)$ sistemi ile tüm $(1 A, 1 B, 1 C)$ sisteminin ağırlık merkezi de yine $G$ noktası olmak zorundadır. Bu durumda $G \in\left[C C_{1}\right]$ ve $|C G|:\left|G C_{1}\right|=2: 1$ elde ederiz. Aynı metotla $G \in\left[B B_{1}\right]$ ve $|B G|$ : $\left|G B_{1}\right|=2: 1$ olduğunu görmek çok kolaydır. Böylelikle $G \in\left[A A_{1}\right] \cap\left[B B_{1}\right] \cap\left[C C_{1}\right]$ olduğunu anlarız ki bu da bize kenarortayların bir noktada kesiştiklerini ve birbirlerini $2: 1$ oranında böldüklerini gösterir.
Teorem 2. $\quad$ Herhangi bir $A B C$ üçgeninde $\left[A A_{1}\right]$, $\left[B B_{1}\right]$, $\left[C C_{1}\right]$ açıortayları bir $N$ noktasında kesişirler ve birbirlerini $|A N|:\left|N A_{1}\right|=$ $(b+c): a,|B N|:\left|N B_{1}\right|=(a+b): b$, $|C N|:\left|N C_{1}\right|=(b+a): c$ oranlarında bölerler.
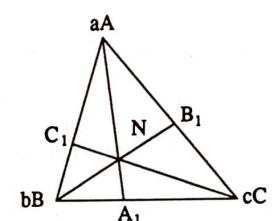
Kanıt. $\quad$ $A$, $B$, $C$ noktalarına sırasıyla $a$, $b$, $c$ kütlelerini yerleştirelim ve $(a A, b B, c C)$ sistemine bakalım. Bu sistemin (G1) özelliğine göre tek bir ağırlık merkezi vardır. (G3) özelliğine göre $B$ ve $C$ noktalarının ağırlık merkezini bulup oraya bu noktaların toplam kütlesini yerleştirirsek sistemin ağırlık merkezi değişmez. $(b B, c C)$ sisteminin ağırlık merkezi $A 1$ noktasıdır. Gerçekten de bu noktada Arşimet’in kol kuralı sağlanır:
$$b \times\left|B A_{1}\right|=c \times\left|A_{1} C\right| .$$
(Üçgende açıortay teorimini hatırlayalım!) Şimdi $\left(a A,(b+c) A_{1}\right)$ sistemine baktığımızda tüm $(a A, b B, c C)$ sisteminin ağırlık merkezinin $\left[A A_{1}\right]$ doğru parçası üzerinde olduğunu görürüz; yani $N \in\left[A A_{1}\right]$. Şimdi de $\left(a A,(b+c) A_{1}\right)$ sistemine kol kuralı uygularsak
$$(b+c) \times\left|N A_{1}\right|=a \times|A N|,$$
buradan da
$$|A N|:\left|N A_{1}\right|=(b+c): a$$
olduğunu görürüz. Benzer olarak $N \in\left[B B_{1}\right]$ ve $N \in\left[C C_{1}\right]$ olduğu kolaylıkla kanıtlanabilir. Bu da açıortayların bir noktada kesiştiğini ve yukarıda verilen oranları sağladığını göstermiş olur.
Not 1. $\quad$ Üçgenin açıortaylarının kesişme noktasının içteğet çemberin merkezi olduğu bilinen bir gerçektir. Yukarıda kanıtladığımız teoremden ise şöyle bir sonuç daha çıkmaktadır: “Eğer $A B C$ üçgeninin tepe noktalarına sırasıyla $a$, $b$, $c$ kütleleri yerleştirilirse elde edilen sistemin ağırlık merkezi içteğet çemberin merkezi olur.”
Örnek. $\quad$ $A B C$ üçgeninin içindeki bir $M$ noktasını üçgenin $A$, $B$, $C$ köşelerine birleştiren $\left[A A_{1}\right]$, $\left[B B_{1}\right]$, $\left[C C_{1}\right]$ doğruları çizilmiştir. $\left|A C_{1}\right|$ : $\left|C_{1} B\right|=p$ ve $\left|A B_{1}\right|:|B C|=q$ olsun. Bu durumda $|A M|:\left|M A_{1}\right|=p+q$ olduğunu gösteriniz.
Çözüm. $\quad$ $A B C$ üçgeninin $A$, $B$, $C$ köşelerine sırasıyla $1$, $p$ ve $q$ yüklerini yerleştirelim; yani $(1 A, p B, q C)$ sistemine bakalım. Bu sistemin ağırlık merkezi $M$ noktasıdır.
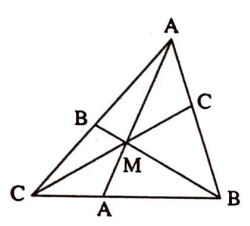
Gerçekten de $\left|A C_{1}\right|:\left|C_{1} B\right|=p$ ise $(1 A, p B)$ sisteminin ağırlık merkezi $1+p$ kütleli $C_{1}$ noktasıdır. (G3) özelliğine göre $(1 A, p B, q C)$ ve $\left((1+p) C_{1}, q C\right)$ sistemlerinin ağırlık merkezleri aynıdır. $((1+p) C, q C)$ sisteminin ağırlık merkezi (G2)’ye göre $\left[C C_{1}\right]$ üzerindedir. Benzer olarak $(1 A, p B, q C)$ sisteminin ağırlık merkezi $\left[B B_{1}\right]$ üzerindedir, yani ağırlık merkezi $\left[C C_{1}\right]$ ve $\left[B B_{1}\right]$ doğru parçalarının kesişme noktası olan $M$ noktasındadır. $A_{1}$ noktasına $p+q$ kütlesini yerleştirirsek $M$ noktası aynı zamanda $(1 A,(p+$ q) $A_{1}$ ) sisteminin de ağırlık merkezi olur. (G2)’ye göre
$$(p+q) \times\left|M A_{1}\right|=1 \times|A M|$$ve buradan da $|A M|:\left|M A_{1}\right|=p+q$ olduğu kanıtlanmış olur.
Soru. $\quad$ Yukarıdaki problemde $M$ noktası $\left[B B_{1}\right]$ ve $\left[C C_{1}\right]$ doğru parçalarını hangi oranda böler?
Ağırlık Merkezinin Özellikleri
Ağırlık merkezinin matematiksel tanımını verelim ve kanıtlayalım ki herhangi bir maddesel noktalar sisteminin ağırlık merkezi gerçekten de (G1), (G2) ve (G3) özelliklerine sahiptir.
Negatif kütleli bir maddesel noktaya fiziksel bir mana vermek güç olmasına rağmen biz tanımımızı yaparken kütlelerin herhangi bir reel sayı olmasına izin vereceğiz. Kütlesi $m$ olan bir maddesel $A$ noktasını biz matematiksel anlamda $m$ reel sayısı ve bir $A$ noktası olarak düşüneceğiz. Yukarıda olduğu gibi $m$ kütleli maddesel bir $A$ noktasını $m A$ ile göstereceğiz.
Tanım. $\quad$ $m_{1} A_{1}, \ldots, m_{n} A_{n}, \quad m_{1}, \ldots, m_{n} \in \mathbb{R}$, $m_{1}+\cdots+m_{n} \neq 0$ sistemi verilmiş olsun. $m_{1} \vec{G A_1}+\cdots+m_{n} \vec{G A_n}=\vec{0}$ şartını sağlayan bir $G$ noktasına bu sistemin ağırlık merkezi denir ve $m_{1}, \ldots, m_{n}$ sayılarına da $G$ ağırlık merkezinin $A_{1}, \ldots, A_{n}$ sistemine göre barisentrik koordinatları adı verilir.
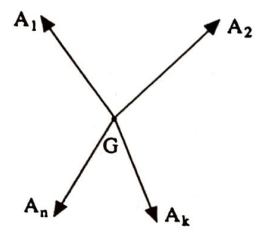
Teorem 3. $\quad$ $G$ noktasının $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezi olması için gerek ve yeter şart herhangi bir $O$ noktası için
$$\Big(m_{1} \vec{OA_1}+\cdots+ m_{n} \vec{OA_n}\Big) :\left(m_{1}+\cdots+m_{n}\right)=\vec{O G} \tag{1}$$ olmasıdır.
Kanıt. $\quad$ $G$ noktası $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezi olsun. Bu durumda
$$ m_{1} \vec{GA_1}+\cdots+m_{n} \vec{GA_n}=\vec{0} \tag{2} $$
olur. $k=1,2, \cdots, n$ için $ \vec{G A_k}= \vec{O A_k}-\vec{O G}$ olduğundan bu eşitliği $(2)$ için kullanırsak $m_{1}\Big(\vec{O A_1}-\vec{O G}\Big)+\cdots+m_{n}\Big(\vec{O A_n}-\vec{O G}\Big)=\vec{0}$, ve $ m_{1} \vec{O A_1}+\cdots+m_{n} \vec{O A_n}=\left(m_{1}+\cdots+m_{n}\right) \vec{O G}$ bulunur.
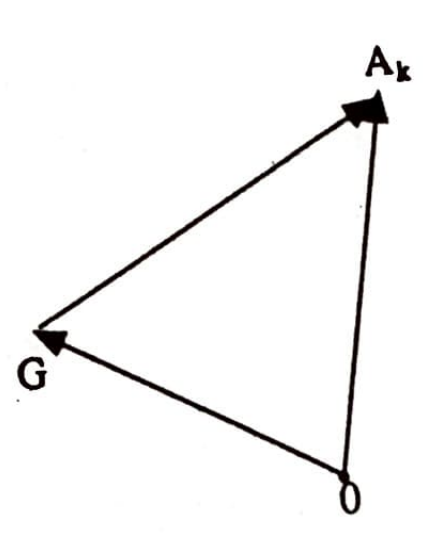
$m_{1}+\cdots+m_{n} \neq 0$ olduğuna göre $\Big(m_{1} \vec{O A_1}+\cdots+m_{n} \vec{O A_n}\Big):\left(m_{1}+\cdots+m_{n}\right)=\vec{O G}$ yazılabilir. Teoremin bir yönde söylediği de budur.
Diğer taraftan, eğer bir $G$ noktası için $(1)$ eşitliği sağlanıyorsa yukarıda yaptıklarımızı ters sıra ile tekrar edersek $G$ noktasının ağırlık merkezi olduğunu görürüz.
Bu teoremden, toplam kütlesi sıfır olmamak kaydıyla, herhangi bir $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezinin var ve tek olduğu derhal anlaşılır. Gerçekten, $O$ herhangi bir nokta olsun. Bu durumda $(1)$ formülü ile tanımlanan bir $\vec{O G}$ vektörünün varlığı ortaya çkar ve bu vektör de (demek ki $G$ noktası da) tek bir şekilde belirlenir.
Böylelikle (G1) özelliği kanıtlanmış oldu.
Teorem 4. İki noktadan oluşan $\left(m_{1} A_{1}, m_{2} A_{2}\right)$ sisteminin ağırlık merkezi $G$, bu noktaları birleştiren doğru parçasının üzerindedir ve bu noktanın yeri “kol kuralı” ile bulunabilir: $$\left|m_{1}\right| \cdot\left|G A_{1}\right|=|m_2| \cdot\left|G A_{2}\right|$$
Kanıt. $\quad$ $G$ noktası $\left(m_{1} A_{1}, m_{2} A_{2}\right)$ sisteminin Teorem 3’e göre var ve tek olan ağırlık merkezi olsun. Tanıma göre $m_{1} \vec{G A_1}+m_{2} \vec{G A_2}=\vec{0}$ ‘dan $$m_{1} \vec{GA_1} =-m_{2} \vec{GA_2} \tag{3}$$ bulunur. Buradan da $\left|m_{1}\right| \cdot\left|G A_{1}\right|=\left|m_{2}\right| \cdot\left|G A_{2}\right|$ elde ederiz. Başka bir deyişle $\left|m_{1}\right| \cdot d_{1}=\left|m_{2}\right| \cdot d_{2}$ yazabiliriz.
Not 2. $\quad$ $(3)$ numaralı eşitlikten kolayca görüldüğü gibi, eğer $m_{1} m_{2}>0$ olursa $G$ noktası $\left[A_{1} A_{2}\right]$ doğru parçasının içinde, $m_{1} m_{2}<0$ olursa dışındadır.
Bu teorem ile (G2) de kanıtlanmış oldu.
Teorem 5. $\quad$ $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminde, $k$ tane noktadan oluşan $\left(m_{1} A_{1}, \ldots, m_{k} A_{k}\right)$ altsistemini ayıralım. Bu noktaların ağırlık merkezi $G_{1}$ olsun. Bu noktaların toplam kütlesini ($m_{1}+\cdots+$ $m_{k} \neq 0$ olmak şartıyla) $G_{1}$ noktasına koyalım. $\left(G_{1}\left(m_{1}+\cdots+m_{k}\right), m_{k+1} A_{k+1}, \ldots, m_{n} A_{n}\right)$ sistemi ile $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezleri aynıdır.
Kanıt. $\quad$ $G$ noktası $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezi olsun. O zaman $m_{1} \vec{GA_1}+\cdots+ m_{n} \vec{GA_n}=\vec{0}$ olur. Şimdi de $\left(m_{1} A_{1}, \cdots, m_{k} A_{k}\right)$ altsistemini düşünelim. Bu sistemin ağırlık merkezi de $G_{1}$ olsun. Teorem 3’e göre
$$ m_{1} \vec{G A_{1}}+\cdots+m_{k} \vec{G A_{k}} =\left(m_{1}+\cdots+m_{k}\right) \vec{GG_1} \tag{4}$$
olmalıdır. $m_{1} \vec{GA_1}+\cdots+m_{k} \vec{GA_k}+m_{k+1} \vec{GA}_{k+1}+\cdots+m_{n} \vec{GA_n}=\vec{0}$ ifadesinde $(4)$ eşitliğini kullanırsak $$\left(m_{1}+\cdots+m_{k}\right) \vec{GG_1}+m_{k+1} \vec{GA}_{k+1}+\cdots+m_{n} \vec{GA_n}=\vec{0}$$ elde ederiz. Bu da bize $G$ noktasının $\left(G_{1}\left(m_{1}+\cdots+m_{k}\right), m_{k+1} A_{k+1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezi olduğunu gösterir.
Uygulamalar
Aşağıdaki alıştırmalar geometri problemlerinin çözümünde çok faydalı olabilirler; bunların kanıtlanmasını okuyucuya bırakıyoruz.
Alıştırma 1. $\quad$ $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sistemindeki bütün noktalarının kütleleri aynı bir $k$ sabitiyle çarpılırsa, sistemin ağırlık merkezi değişmez.
Alıştırma 2. $\quad$ $G$ noktası $\left(m_{1} A, m_{2} B, m_{3} C\right)$ sisteminin ağırlık merkezi ise, $A G$ doğrusu $B C$ kenarını $\left(m_{2} B, m_{3} C\right)$ sisteminin ağırlık merkezi olan $A_{1}$ noktasında keser.
Alıştırma 3. $\quad$ $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminde herhangi bir noktanın kütlesini “parçalarsak” sistemin ağırlık merkezi değişmez. Örneğin $m_{1}=m_{11}+\cdots+m_{1 k}$ şeklinde parçalanırsa, $\left(m_{11} A_{1}, \ldots, m_{1 k} A_{1}, m_{2} A_{2}, \ldots, m_{n} A_{n}\right)$ sistemi ile $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}\right)$ sisteminin ağırlık merkezi aynıdır.
Alıştırma 4. $\quad$ Eğer bir $G$ noktası hem $\left(m_{1} A_{1}, m_{2} A_{2}, \ldots, m_{n} A_{n}\right)$ sisteminin, hem de $\left(p_{1} B_{1}, p_{2} B_{2}, \ldots, p_{k} B_{k}\right)$ sisteminin ağırlık merkezi ise, bu $G$ noktası aynı zamanda bütün $\left(m_{1} A_{1}, \ldots, m_{n} A_{n}, p_{1} B_{1}, \ldots, p_{k} B_{k}\right)$ sisteminin ağırlık merkezidir.
Alıştırma 5. $\quad$ Not 1’de $A B C$ üçgeninin içteğet çemberinin merkezinin, $(a A, b B, c C)$ sisteminin ağırlık merkezi olduğunu gördük. $A B C$ üçgeninin $a$ kenarına ait dışteğet çemberinin (yani $[B C]$ kenarına teğet ve $[A B]$ ve $[A C]$’nin de uzantılarına teğet olan çemberin) merkezinin $(a A,-b B,-c C)$ sisteminin ağırlık merkezi olduğunu gösteriniz.
Problem 1. (Matematik Dünyası, problem Y28) Bir $A B C D$ dışbükey dörtgeni üzerinde $\lambda=|P A|:|P B|=|R D|:|D C|$ ve $\mu=|Q B|:|Q C|=|S A|:|S D|$ olmak üzere $P$, $Q$, $R$, $S$ noktaları alınıyor. $[P R]$ ve $[Q S]$ doğruları $T$ noktasında kesişiyorsa, $|T S|:|T Q|=\lambda$ ve $|T P|:|T R|=\mu$ olduğunu gösteriniz.
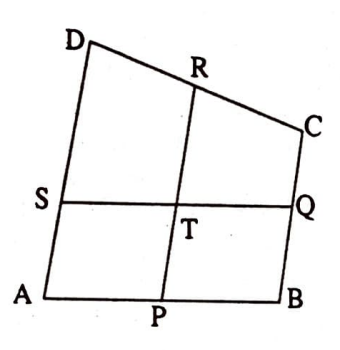
Çözüm. $\quad$ $A$, $B$, $D$, $C$ noktalarına sırasıyla $1$, $\lambda$, $\mu$ ve $\lambda \mu$ yüklerini yerleştirelim ve $(1A, \lambda B, \mu D, \lambda \mu C)$ sistemine bakalım. $|P A|=\lambda|A B|$ olduğundan (G2) özelliğine göre $(1 A, \lambda B)$ sisteminin ağırlık merkezi $1+\lambda$ kütleli $P$ noktası olacaktır. Bunu şöyle gösterelim: $$(1+\lambda) P=(1 A, \lambda B).$$
Benzer olarak $(\mu D, \lambda \mu C)$ sisteminin ağırlık merkezi $\mu+\lambda \mu$ kütleli $R$ noktası olacaktır: $$(\mu+\lambda \mu) R=(\mu D, \lambda \mu C) .$$
O zaman $(1 A, \lambda B, \mu D, \lambda \mu C)$ sisteminin ağırlık merkezi $[R P]$ doğru parçası üzerindedir ve (G2)’ye göre $$ (\mu+\lambda \mu)|G R|=(1+\lambda)|G P| $$ veya $$ |G P|:|G R|=(\mu+\lambda \mu):(1+\lambda)=\mu $$ elde ederiz. Şimdi $(1 A, \lambda B, \mu D, \lambda \mu C)$ sistemini $(1 A, \mu D)$ ve $(\lambda B, \lambda \mu C)$ altsistemlerine ayırıp ağırlık merkezimizi bir de bu şekilde bulalım. $(1 A, \mu D)$ sisteminin ağırlık merkezi $1+\mu$ kütleli $S$ noktası, $(\lambda B, \lambda \mu C)$ sisteminin ağırlık merkezi ise $\lambda+\lambda \mu$ kütleli $Q$ noktası olur. Bu durumda tüm sistemin ağırlık merkezi $G$, $[SQ]$ doğru parçası üzerindedir ve (G2)’ye göre
$$(1+\mu)|G S|=(\lambda+\lambda \mu)|G Q|$$ veya $$|G S|:|G Q|=(\lambda+\lambda \mu):(1+\mu)=\lambda$$ elde ederiz. Böylece $(1 A, \lambda B, \mu D, \lambda \mu C)$ sisteminin ağırlık merkezi $[R P]$ ve $[S Q]$ doğru parçalarını üzerinde olmalıdır. Bu da $G$ noktasının bu iki doğru parçasının ortak noktası olan $T$ noktası olduğunu gösterir. Dolayısıyla $T=G$ yazarsak istenilenin kanıtlanmış olduğu görülür.
Problem 2. Eğer $G$ noktası $A B C$ üçgeninin içinde herhangi bir nokta ise, $A$, $B$, $C$ köşelerine sırasıyla öyle $m_{1}$, $m_{2}$, $m_{3}$ kütleleri yerleştiriniz ki $G$ noktası $\left(m_{1} A, m_{2} B, m_{3} C \right)$ sisteminin ağırlık merkezi olsun.
Çözüm. $\quad$ $A$ ve $G$ noktalarından geçen ve $B C$ kenarını $A_{1}$ noktasında kesen $A A_{1}$ doğrusunu çizelim. $\left|B A_{1}\right|=d_{1},\left|C A_{1}\right|=d_{2},|A G|=d_{3}$, $\left|G A_{1}\right|=d_{4}$ olsun. $d_{1} d_{4}+d_{2} d_{4}=m_{1}, d_{3} d_{2}=$ $m_{1}, d_{1} d_{3}=m_{3}$ olsun. Bu durumda $A_{1}$ noktası $\left(m_{2} B, m_{3} C\right)$ sisteminin ağırlık merkezi, $G$ noktası ise $\left(m_{1} A, m_{2} B, m_{3} C\right)$ sisteminin ağırlık merkezi olur.
Problem 3. (Seva Teoremi) $A B C$ üçgeninin $[B C]$, $[C A]$ ve $[A B]$ kenarları üzerinde sırasıyla $A_{1}$, $B_{1}$, $C_{1}$ noktaları alınıyor.
$$ \frac{\left|B A_{1}\right|}{\left|A_{1} C\right|} \cdot \frac{\left|C B_{1}\right|}{\left|B_{1} A\right|} \cdot \frac{\left|A C_{1}\right|}{\left|C_{1} B\right|}=1 \tag{5} $$
olduğuna göre, $A A_{1}$, $B B_{1}$, $C C_{1}$ doğrularının bir noktada kesiştiğini gösteriniz.
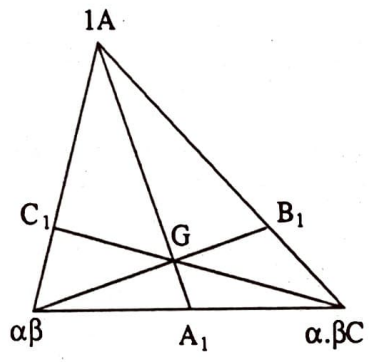
Çözüm. $\quad$ $\left|A C_{1}\right|:\left|C_{1} B\right|=\alpha$, $\left|B A_{1}\right|:\left|A_{1} C\right|=\beta$, $\left|C B_{1}\right|:\left|B_{1} A\right|=\gamma$ olsun. Verilen şarta göre $\alpha \beta \gamma=1$ olur. $A$, $B$, $C$ noktalarına sırasıyla $1$, $\alpha$, $\alpha \beta$ yüklerini yerleştirip, $(1 A, \alpha B, \alpha \beta C)$ sistemini gözönüne alalım. $\left|A C_{1}\right|=\alpha\left|C_{1} B\right|$ olduğundan, $C_{1}$ noktası $(1 A, \alpha B)$ sisteminin ağırlık merkezi olur. Benzer şekilde $A_{1}$ noktası $(\alpha \beta, \alpha \beta C)$ sisteminin ve $B_{1}$ noktası da $(1 A, \alpha B, \alpha \beta C)$ sisteminin ağırlık merkezi olur. $(1 A, \alpha B, \alpha \beta C)$ sisteminin ağırlık merkezini $G$ ile gösterelim. Ağırlık merkezi olan $G$, hem $\left[A A_{1}\right]$, hem $\left[B B_{1}\right]$, hem de $\left[C C_{1}\right]$ doğru parçalarının üzerinde olmalıdır. Bu bize bu doğru parçalarının bir noktada ($G$ noktasında) kesiştiğini gösterir.
Problem 4. (Seva Teoremi’nin tersi) Eğer herhangi bir $A B C$ ü̧geninde $\left[A A_{1}\right]$, $\left[B B_{1}\right]$, $\left[C C_{1}\right]$ doğruları bir noktada kesişiyorlarsa, Problem 3’te verilen $(5)$ koşulu sağlanır.
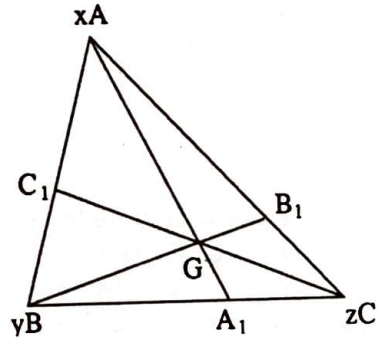
Çözüm. $\quad$ $\left[A A_{1}\right]$, $\left[B B_{1}\right]$, $\left[C C_{1}\right]$ doğrularının bir $G$ noktasında kesiştiklerini farzedelim. $A$, $B$, $C$ noktalarına, $G$ noktasını sistemin ağırlık merkezi yapacak sekilde, sırasıyla $x$, $y$, $z$ kütlelerini yerleştirelim. (Bunun mümkün olduğunu Problem 2’den biliyoruz.) O zaman $G$’den geçen $\left[A A_{1}\right]$ doğrusu $[B C]$ kenarını $(y B, z C)$ sisteminin ağırlık merkezi olan $A_{1}$ noktasında keser. (G2) özelliğine göre $A_{1}$ noktasında $y\left|B A_{1}\right|=z\left|A_{1} C\right|$ bağıntısı vardır. Benzer şekilde $\left|A C_{1}\right|=y\left|C_{1} B\right|$ ve $x\left|B_{1} A\right|=z\left|B_{1} C\right|$ bağıntılarını kolaylıkla bulabiliriz. Buradan $\left|B A_{1}\right|:\left|A_{1} C\right|=z: y$, $\left|A C_{1}\right|:\left|C_{1} B\right|=y: x$ ve $\left|B_{1} A\right|:\left|B_{1} C\right|=x: z$ elde ederiz. Bu üç eşitliği taraf tarafa çarparsak Seva şartının sağlandığını görürüz.
Problem 5. (Newton Teoremi) $A B C D$ teğetler dörtgeninin içteğet çemberinin merkezi, bu dörtgenin köşegenlerinin orta noktalarını birleştiren doğru parçasının üzerindedir.
Çözüm. $\quad$ $M$ noktası çemberin merkezi, $F$ noktası ise $[B C]$ ve $[A D]$ kenarlarının uzantılarının kesişme noktası ve $E$, $K$ noktaları da $[A C]$ ve $[B D]$ köşegenlerinin orta noktaları olsun.
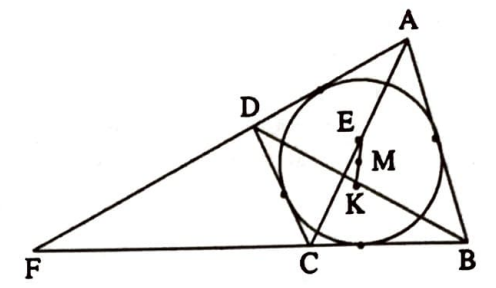
Baktığımız çember $A B F$ üçgeninin içteğet çemberi olduğu için bu çemberin merkezi olan $M$ noktası, $m_{1}=|B F|$, $m_{2}=|A F|$, $m_{3}=|A B|$ alınırsa $\left(m_{1} A, m_{2} B, m_{3} F\right)$ sisteminin ağırlık merkezi olur (Not 1). Bu çember aynı zamanda $D C F$ üçgeninin $f$ kenarına ait dışteğet çemberi olduğu için, $M$ noktası aynı zamanda $\left(m_{4} C, m_{5} D, m_{6} F\right)$ sisteminin de ağırlık merkezi olur ($m_{4}=-|D F|$, $m_{5}=-|C F|$, $m_{6}=|C D|$, Alıştırma 5). Dolayısıyla $M$ noktası $\left(m_{1} A, m_{2} B, m_{3} F, m_{4} C, m_{5} D, m_{6} F\right)$ sisteminin ağırlık merkezi olur (Alıştırma 4). Diğer taraftan $m_{3}+m_{6}=m_{1}+m_{2}+m_{4}+m_{5}$ olduğundan ( $A B C D$ kirişler dörtgeni), $|A B|+|D C|=|A D|+|B C|$ eşitliğini elde ederiz. $F$ noktasına baktığımızda bu noktanın hem $\left(m_{1} C, m_{5} B\right)$, hem de $\left(m_{2} D, m_{4} A\right)$ sisteminin ağırlık merkezi olduğunu görürüz. Yani $F$ noktası $\left(m_{1} C, m_{5} B, m_{2} D, m_{4} A\right)$ sisteminin ağırlık merkezidir.
Böylece kütleyi parçalama (Alıştırma 3) fikrini kullanarak $M$ noktasının aşağıda yazdığımız sistemlerin ağırlık merkezi olduğunu görürüz: ($M=(a A, b B)$ şeklindeki bir eşitliği, “$M$ noktası $(a A, b B)$ sisteminin ağırlık merkezidir” manasında kullanacağız.)
$$\begin{split} M= & \left(m_{1} A, m_{2} B, m_{3} F, m_{4} C, m_{5} D, m_{6} F\right) \\
= & \left(m_{1} A, m_{2} B, m_{4} C, m_{5} D,\left(m_{3}+m_{6}\right) F\right) \\
= & \left(m_{1} A, m_{2} B, m_{4} C, m_{5} D, m_{4} A, m_{5} B, m_{1} C, m_{2} D\right) \\
= & \left(\left(m_{1}+m_{4}\right) A,\left(m_{1}+m_{4}\right) C, \left(m_{2}+m_{5}\right) B,\left(m_{5}+m_{2}\right) D\right) \\
= & \left(2\left(m_{1}+m_{4}\right) E, 2\left(m_{2}+m_{5}\right) K\right) \end{split}$$
Böylece $M$ noktasının kütlesi $2\left(m_{1}+m_{4}\right)$ olan $E$ ile, kütlesi $2\left(m_{2}+m_{5}\right)$ olan $K$ noktasının ağırlık merkezi olduğunu görürüz. (G2) özelliğine göre $M$ noktası $E$ ve $K$ noktalarını birleştiren doğru parçası üzerindedir.
Problemler
Aşağıdaki problemleri önce alıştığınız yolla çözmeye çalışınız. Sonra bu yazıda kullanılan metotlarla çözünüz. Mekanik kavramlarının kolaylıklar sağladığını göreceksiniz.
- $A B C$ üçgeninin ağırlık merkezinin, çevrel çemberinin merkezi olması için, $A$, $B$, $C$ köşelerine yerleştirilmesi gereken kütle miktarlarını bulunuz.
- Herhangi bir üçgenin yüksekliklerinin bir noktada kesiştiklerini gösteriniz.
-
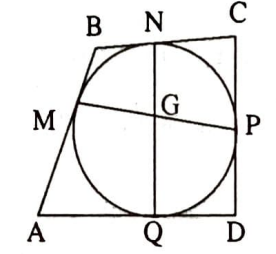
$A B C D$ teğetler dörtgeni çembere $M$, $N$, $P$, $Q$ noktalarında teğet ve $|A M|=a$, $|M B|=b$, $|C N|=c$, $|D Q|=d$ olsun. $|M G|:|G P|$ ve $|N G|:|G Q|$ oranlarını bulunuz.
$\quad$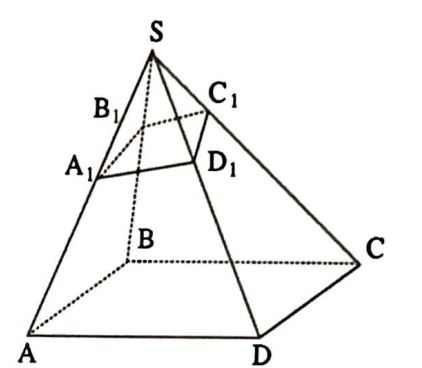 
$S A B C D$ piramidinin tabanı $A B C D$ paralelkenarıdır. $p$ düzlemi bu piramidin $S A$, $S B$, $S C$, $S D$ kenarlarını sıra ile $A_{1}$, $B_{1}$, $C_{1}$, $D_{1}$ noktalarında kesiyor ve $\left|S A_{1}\right|=\frac{|S A|}{3}$, $\left|S B_{1}\right|=\frac{|S B|}{5}$, $\left|S C_{1}\right|=\frac{|S C|}{4}$ veriliyor. $\frac{\left|S D_{1}\right|}{|S D|}$ oranını bulunuz.
$\quad$
$\quad$
Yazarlar, bu makaledeki konunun incelenmesinde, biçim verilmesinde ve müzakere edilmesinde büyük yardım göstermiş olan sayın Ruza Burak’a derin minnettarlıklarını sunarlar.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.
