Yazar: Ali Nesin (California Üniversitesi (Irvine) Matematik Bölümü öğretim üyesi)
Yıl: 1994
Sayı: 5
Yoksulun Şansı
Bölümleri birbirinden bağımsız olan bu yazı dizisinin okumak üzere olduğunuz bölümü girişe gereksinmiyor. Doğrudan kanıtlayacağımız sonuca geçelim:
“Teorem.” Yoksulun zengine karşı şansı yoktur.
Bu çok bilinen ‘teorem’i kanıtlayabilmek için her şeyden önce önermeyi matematikselleştirmeliyiz. Zenginin –tanımı gereği– çok parası var. Yoksulunsa az parası var. Zenginle yoksul yazı-tura oynayacaklar. Yazı gelirse yoksul zenginden 1 lira alacak. Tura gelirse yoksul zengine 1 lira verecek. Oyun iki oyuncudan birinin parası bitene dek sürerecek. Daha önce sona eremez. Bu kuralla oyun hiç bitmeyip sonsuza dek sürebilir. Örneğin yazı-tura atışlarını sırayla bir yoksul bir zengin kazanırsa oyun sonsuza dek sürer. Bu oyun sonsuza dek sürebilir ama sonsuza dek sürme olasılığı sıfırdır. Bunu geçen yazımızda kanıtlamıştık. Bu bölümde yukarıdaki yazı-tura oyununu kaç olasılıkla kimin kazandığını bulacağız. Önce paranın hilesiz olduğunu varsayacağız; bu bölümün sonunda hileli parayla oynanan yazı-tura oyunlarını inceleyeceğiz.
İki oyuncudan birinin kesinlikle (yani 1 olasılıkla) kazanacağını biliyoruz. Hangi oyuncunun kaç olasılıkla kazanacağını bulmak istiyoruz. Örneğin birinci oyuncunun 1, ikinci oyuncunun 100 lirası varsa, büyük bir olasılıkla ikinci oyuncu oyunu kazanır. Birinci oyuncunun kazanma olasılığı azdır, ama 0 değildir. Okurun, “yüzde 1 olasılıkla birinci, yüzde 99 olasılıkla ikinci oyuncu kazanır” dediğini duyar gibi oluyorum. Doğru değil. Yanıt yanlış ama okuru yanılgıya bilerek sürükledim. Bir başka örnek ele alalım.
Diyelim birinci oyuncunun 2, ikinci oyuncunun 3 lirası var. Birinci oyuncunun oyunu kazanma olasılığı kaçtır? Bu kez okur 2/5 yanıtını verecek ve haklı çıkacaktır. Bir önceki örnekte, birinci oyuncunun kazanma olasılığı 1/101’dir, ikinci oyuncununkiyse 100/101’dir. Bu bölümde, oyuna birinci oyuncu $n$, ikinci oyuncu $m$ lirayla başladığında, birinci oyuncunun oyunu $\frac{n}{n+m}$ olasılıkla kazanacağını kanıtlayacağız.
Teorem 1. Hilesiz parayla oynanan yazı-tura oyununa birinci oyuncu $n$ lirayla, ikinci oyuncu $m$ lirayla başlarsa, birinci oyuncu oyunu $\frac{n}{n+m}$ olasılıkla kazanır.
Teoremi bir an için kanıtlanmış varsayıp, önemli bir sonucunu irdeleyelim. Teoreme göre, ikinci oyuncunun ne kadar çok parası varsa, birinci oyuncunun kazanma şansı o kadar azdır. Çünkü $n$ sabit kalırsa ve $m$ artarsa, $\frac{n}{n+m}$ sayısı gittikçe küçülür. Zengin ne denli zenginse ve yoksul ne denli yoksulsa, yoksulun kazanma olasılığı o denli azdır. Biraz abartalım ve zenginin sonsuz parası olduğunu varsayalım. (Para mı basıyor ne!) O zaman, yoksulun oyunun (sonlu) bir anında beş parasız kalma olasılığı 1 olacak. Yani yoksul yüzde yüz kaybedecek. Oyuna kaç parayla başlarsa başlasın … Çünkü $m$ sonsuza gittiğinde $\frac{n}{n+m}$ sayısı sıfıra gider. Yoksul milyoner olarak oyuna başlasa bile, zenginin sonsuz parası varsa kesinlikle kaybeder. Dolayısıyla bu teoremden şu çıkar:
Birinci Teoremin Bir Sonucu. Hilesiz parayla oynanan bir yazı-tura oyununda, birinci oyuncunun sonlu, ikinci oyuncunun sonsuz parası varsa, oyunu 1 olasılıkla (yani yüzde yüz) ikinci oyuncu kazanır.
Şimdi teoremimizi kanıtlayalım. $s=n+m$ olsun. Yani $s$, iki oyuncunun toplam parası. $p_{s}(n)$, birinci oyuncunun $n$, ikinci oyuncunun $s-n$ lirası olduğunda, birinci oyuncunun oyunu kazanma olasılığı olsun. Örneğin, $p_{s}(0)=0$. Çünkü birinci oyuncunun hiç parası yoksa, zaten oyunu kaybetmiştir ve kazanma olasılığı yoktur. Öte yandan, $p_{s}(s)=1$. Çünkü birinci oyuncunun $s$ lirası varsa, ikinci oyuncunun hiç parası kalmamıştır ve oyunu birinci oyuncu kazanmıştır. Teorem 1, $p_{s}(n)$ sayısının $n / s$ olduğunu söylüyor. Demek ki
$$p_{s}(n)=\frac{n}{s} \tag{1}$$ eşitliğini kanıtlamalıyız. $p_{s}(n)$ sayıları birbirinden bağımsız değillerdir. Aralarında bir ilişki vardır. Bu ilişkiyi bulalım. $0<n<s$ olsun. Birinci oyuncunun $n$ lirası var. Oyun, iki yoldan birini alabilir. Birinci oyuncu ya kazanacaktır ya kaybedecektir. Kazanırsa $n+1$ lirası olacaktır, kaybederse de $n-1$ lirası. Her iki durumun da olasılığı 1/2’dir. Demek ki $n$ lirayla oyuna başlayan birinci oyuncunun ilk oyundan sonra yarım olasılıkla $n-1$ lirası, yarım olasılıkla da $n+1$ lirası olacaktır elinde. Bu son iki durumda birinci oyuncunun oyunu kazanma olasılığı, sırasıyla, $p_{s}(n-1)$ ve $p_{s}(n+1)$’dir. Yani, $0<n<s$ ise,
$$p_{s}(n)=\frac{p_{s}(n-1)}{2}+\frac{p_{s}(n+1)}{2}$$
dir. Bunu şöyle de yazabiliriz: $0<n<s$ için,
$$p_{s}(n+1)=2 p_{s}(n)-p_{s}(n-1) . \tag{2}$$
Şimdi bir önsav kanıtlayalım:
Önsav. Eğer $0<n \leq s$ ise, $p_{s}(n)=n p_{s}(1)$.
Önsavın Kanıtı. $n$ üzerine tümevarımla kanıtlayacağız. Eğer $n=1$ ise, kanıtlanacak eşitlik $p_{s}(1)=p_{s}(1)$ olur ve bu durumda önsavın doğruluğu apaçık. Şimdi eşitliği $n=2$ için kanıtlayalım. $p_{s}(2)=2 p_{s}(1)$ eşitliğini kanıtlamak istiyoruz. $(2)$ eşitliğinden, $$p_{s}(2) \stackrel{(2)}{=} 2 p_{s}(1)-p_{s}(0)$$ elde ederiz. Ama $p_{s}(0)=0$ eşitliğini biliyoruz. Demek ki, $p_{s}(2)=2 p_{s}(1)$ ve bu durumda da önsavımız kanıtlanmıştır. Şimdi $n \geq 3$ olsun. Önsavın $n-1$ ve $n$ için doğru olduğunu varsayıp $n+1$ için kanıtlayalım. Bu varsayımlardan ve $(2)$ eşitliğinden,$$\begin{split}
p_{s}(n+1) & \stackrel{(2)}{=} 2 p_{s}(n)-p_{s}(n-1) \
& =2 n p_{s}(1)-(n-1) p_{s}(1) \
& =(n+1) p_{s}(1)
\end{split}
$$ çıkar. Önsavımız kanıtlanmıştır.
Yukarıdaki önsavda $n=s$ alalım: $1=p_{s}(s)=s p_{s}(1)$ buluruz, yani $p_{s}(1)=1 / s$. Önsavı bir kez daha uygularsak bu eşitlikten $p_{s}(n)=n / s$ çıkar. Teoremimiz kanıtlanmıştır.
Hileli Paranın Öyküsü. Bölümün süreğinde paranın hileli olduğunu varsayacağız$^1$. Yazı gelme olasılığına $y$ diyelim. Birinci oyuncu yazı geldiğinde kazansın. Tura gelme olasılığı $t$ olsun. $y+t=1$ eşitliği geçerli elbet. Toplam paraya gene $s$ diyeceğiz. $p_{s}(n)$, birinci oyuncunun –yani yazı geldiğinde kazanan oyuncunun– $n$ lirası varken öbür oyuncunun bütün parasını ütme olasılığı olsun. Eğer $y=0$ ise, yani para hiç yazı gelmeyecekçesine hileliyse, oyunu ikinci oyuncu kazanır elbet. Eğer $y=1$ ise, birinci oyuncu oyunu kazanır. Ayrıca $y=1 / 2=t$ şıkkını yukarıda irdelemiştik. Demek ki, bundan böyle $0<y<1$ ve $t \neq y$ eşitsizliklerini varsayabiliriz. Bu varsayımla oyunun sonsuza değin sürme olasılığının sıfır olduğunu geçen yazının sonunda göstermiştik.
Teorem 2. Yazı gelme olasılığının $y$, tura gelme olasılığının $t$ olduğunu varsayalım $(t=1-y)$. Birinci oyuncu yazı geldiğinde kazansın ve oyuna $n$ lirayla başlasın. İkinci oyuncunun $s-n$ lirası olsun. Birinci oyuncunun yazı-tura oyununu kazanma olasılığı $\frac{y^{s}-y^{s-n} t^{n}}{y^{s}-t^{s}}$’dir.
$(2)$ formülünün bir benzerini bulalım önce. Birinci kanıttaki gibi bir akıl yürütmeyle, $$p_{s}(n)=t p_{s}(n-1)+y p_{s}(n+1)$$ eşitliğini buluruz. Bundan da $$p_{s}(n+1)=\frac{p_{s}(n)}{y}-\frac{t p_{s}(n-1)}{y} \tag{3}$$ çıkar. Aynen birinci kanıttaki gibi yapacağız. $p_{s}(n)$ sayısını $p_{s}(1)$’i kullanarak bulacağız.
Önsav. Eğеr $0<n \leq s$ ise$^{2}$, $$p_{s}(n)=\frac{y^{n}-t^{n}}{y^{n-1}(y-t)} p_{s}(1).$$
Önsavın Kanıtı. $n$ üzerine tümevarımla kanıtlayacağız. $n=1$ için bir sorun yok. $n=2$ için kanıtlayalım. $(3)$ eşitliğinde $n=1$ alırsak ve $p_{s}(0)=0$, $y+t=1$ eşitliklerini kullanırsak, önsavın $n=2$ için doğru olduğunu buluruz. Şimdi formülün $n$ ve $n-1$ sayıları için doğru olduğunu varsayıp $n+1$ için kanıtlamak gerekiyor. Ayrıntıları okura bırakıyoruz.
Artık ikinci teoremi kanıtlayabiliriz. Yukarıdaki önsavda $n=s$ alırsak ve $p_{s}(s)=1$ eşitliğini kullanırsak, $$p_{s}(1)=\frac{y^{s-1}(y-t)}{y^{s}-t^{s}} $$ buluruz. Bu eşitliği önsava uygulayarak
$$ p_{s}(n)=\frac{y^{n}-t^{n}}{y^{n-1}(y-t)} \frac{y^{s-1}(y-t)}{y^{s}-t^{s}}$$
buluruz. Sadeleştirerek, $$p_{s}(n)=\frac{y^{s}-y^{s-n} t^{n}}{y^{s}-t^{s}} \tag{4}$$ eşitliğini buluruz. İkinci teorem de kanıtlanmıştır.
Birinci oyuncuda $n$ lira, ikinci oyuncuda sonsuz para varsa, birinci oyuncunun oyunu kazanma olasılığı nedir? Bu soruyu yanıtlayalım. Bu sorunun yanıtını bulmak için $\lim_{s\rightarrow \infty} p_s(n)$ sayısını bulmalıyız, yani $(4)$ eşitliğindeki $s$ sayısını sonsuza göndermeliyiz. Bu limitin hesaplanması $y<t$ yada $t<y$ olduğuna göre değişir, ama bulunan sonuç değişmez, her iki şıkta da sıfır bulunur:
İkinci Teoremin Bir Sonucu. Yazı gelme olasılığı $y$ olsun ve $y<1$ olsun. Birinci oyuncu yazı gelince kazansın ve ikinci oyuncunun sonsuz parası olsun. Birinci oyuncu 1 olasılıkla (yani % 100) bütün parasını kaybedecektir.
Örneğin %99 olasılıkla yazı bile gelse, eğer tura geldiğinde kazananın sonsuz parası, yazı geldiğinde kazananın sonlu parası varsa, oyunu önünde sonunda sonsuz parası olan kazanır. Sonsuz için doğru olan büyük sayılar için de doğrudur aşağı yukarı: para tek yanlı olmadıkça (yani $y<1$ oldukça), zengin çok zenginse yazı-tura oyununu büyük bir olasılıkla kazanır.
Züğürt Tesellisi
Önceki bölümde, yazı-tura oyununda yoksulun zengine karşı şansının çok az olduğunu kanıtladık. Öyle ki, zengin sonsuz zengin olduğunda oyunu 1 olasılıkla (yani yüzde yüz) kazanacaktır. Bu bölümde bu olgudan güzel bir eşitlik çıkaracağız:
$$\sum_{k=1}^{\infty} \frac{1}{(k+1) 4^{k}}\left(\begin{array}{c} 2 k \\ k \end{array}\right)=1 .$$
Yoksulun cebinde 1 lira olduğunu varsayalım. Zenginin de sonsuz zengin olduğunu, yani sonsuz parası olduğunu varsayalım. Dolayısıyla zenginin parası bitmez ve zengin oyunu kaybedemez. Yoksulun tek şansı sonsuza değin oynayabilmek. Bunun da olasılığının sıfır olduğunu daha önceki bölümden biliyoruz.
Birinci yazı-tura atıldı. Tura gelirse yoksulun cebindeki tek lira gidecek, beş parasız kalacak ve oyun bitecek. Diyelim ilk oyunu yoksul kazandı. Şimdi cebinde iki lirası var. İkinci oyunda kaybederse gene 1 lirası kalacak, kazanırsa 3 lirası olacak. Oyun böylece, sürebildiğince, yani yoksulun parası olduğu sürece sürecek.
Oyunun alabileceği bütün durumları bir ‘ağaç’la gösterebiliriz. Ağacın en tepesine 1 yazalım. Bu 1, yoksulun oyuna başlamadan önceki bütün serveti. 1’den sonra aşağıya doğru sağlı sollu iki ok (kök) çıkaralım. Bu oklardan soldakinin ucuna 0 , sağdakinin ucuna 2 yazalım. Soldaki ok, yoksulun kaybettiğini, sağdakiyse kazandığını gösteriyor. 0 ve 2 sayıları da, birinci oyunun sonunda yoksulun cebindeki para. Kaybederse 0, kazanırsa 2 lirası olacak. Kaybettiğinde oyun duruyor, dolayısıyla 0’dan sonra kök büyümüyor. Kazanmışsa, yani 2 lirası olmuşsa oyun sürüyor. 2’den sonra kök büyüyor, ikiye ayrılıyor. Soldaki kök her zaman yoksulun kaybettiğini gösterecek, sağdakiyse kazandığını. Oyun sonsuza dek uzayabileceğinden, ağacın kökleri sonsuza dek uzar. Bu sonsuz ağaçtan bir bölüm sunalım:
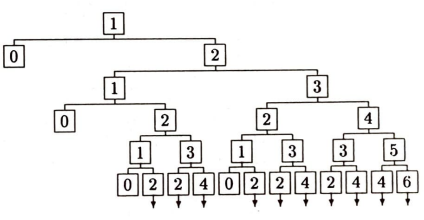
Daha ilk turda yoksulun oyunu kaybetme olasılığı $1/2$ elbet: tura gelirse kaybedecek ve oyunu bir daha hiç oynayamayacak, yani elenecek. Yoksul, ilk turda kaybetmemişse ikinci turda elenemez, çünkü yukarıdaki ağacın üstten üçüncü katında 0 yok. Ama üçüncü turda elenebilir. Eğer sırasıyla yazı-tura-tura (YTT) gelirse yoksul beş parasız kalacaktır. Sırasıyla yazı-tura-tura (yani YTT) gelme olasılığıysa $1 / 2^{3}$, yani $1/8$’dir. Demek ki yoksulun üçüncü turda elenme olasılığı $1 / 8$. Birinci turda elenme olasılığı da $1/2$’ydi. Bu olasılıkları toplarsak, yoksulun üç oyun dayanamama olasılığını buluruz: $1 / 2+1 / 8=5 / 8$. Yoksul ilk üç tur dayanabilmişse, dördüncü turu oynamaya hak kazanır. Bu turda elenemez, çünkü en az 1 lirası kalacaktır. Ancak beşinci turda elenebilir. Sırasıyla YTYTT ya da YYTTT gelirse elenecektir. $n \geq 1$ herhangi bir doğal sayı olsun. Yukarıdaki ağacın (üstten) $n$’yinci katında kaç tane 0, kaç tane 1 , kaç tane 2 vardır? Bu sayılara $p_{n}(0)$, $p_{n}(1)$, $p_{n}(2)$ diyelim. Genel olarak, $0 \leq k \leq n$ ise $$ p_{n}(k)=\text { ağacın } n \text {‘yinci katındaki } k \text { sayısı } $$ olsun. Örneğin,
$$\begin{array}{llllll}
p_{1}(0)=0, & p_{1}(1)=1, & & & &\\
p_{2}(0)=1, & p_{2}(1)=0, & p_{2}(2)=1 & & &\\
p_{3}(0)=0, & p_{3}(1)=1, & p_{3}(2)=0 & p_{3}(3)=1 & &\\
p_{4}(0)=1, & p_{4}(1)=0, & p_{4}(2)=2 & p_{4}(3)=0 & p_{4}(4)=1 &\\
p_{5}(0)=0, & p_{5}(1)=2, & p_{5}(2)=0 & p_{5}(3)=3 & p_{5}(4)=0 & p_{5}(5)=1.
\end{array} $$
Bu sayıları nasıl bulabiliriz? Örneğin $p_{6}(4)$’ü ağaca bakmadan bulabilir miyiz? $p_{6}(4)$, ağacın altıncı katındaki 4’lerin sayısı. Altıncı kattaki 4 sayıları bir üst kattaki 3 ve 5 sayılarından gelir; dolayısıyla $$p_{6}(4)=p_{5}(3)+p_{5}(5)=3+1=4$$ eşitliği geçerlidir. Bunun gibi, her $2 \leq k<n$ için $$p_{n}(k)=p_{n-1}(k-1)+p_{n+1}(k+1) \tag{1}$$ eşitliği geçerlidir. Çünkü $n$’yinci sıradaki $k$’ler ancak $n-1$’inci sıradaki $k-1$ ve $k+1$’lerden gelebilirler. $p_{n}(0)$ ve $p_{n}(1)$ sayıları için formülümüz değişik. $n$’yinci sıradaki 0 sayıları, $n-1$’inci sıradaki 1 sayılarından gelebilir ancak. Bunun gibi, $n$’yinci sıradaki 1 sayıları bir önceki sıradaki 2 sayılarından gelebilir${ }^{3}$. Dolayısıyla $$p_{n}(0)=p_{n-1}(1)=p_{n-2}(2) \tag{2}$$
eşitlikleri geçerlidir. $$ p_{n}(n)=1 \tag{3}$$ eşitliğini bulmak da zor değildir. Yukarıdaki eşitlikleri kullanarak bir tablo çizelim. (Bu tabloda $p_{n}(k)$ sayısını $n$’yinci sırayla $k$’yinci sütunun kesiştiği yere koyduk.)
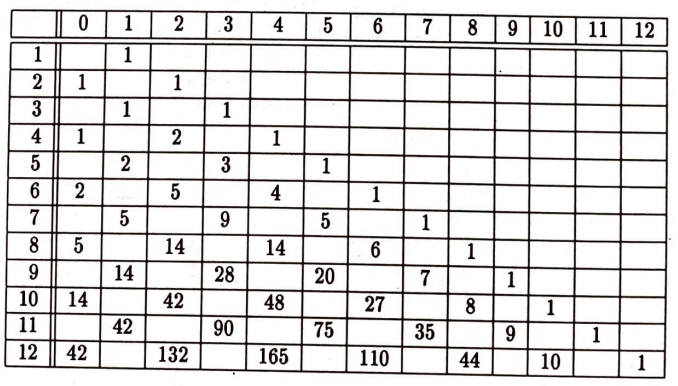
Oyunun ikinci katta (yani birinci atıştan hemen sonra) bitme olasılığı $1 / 2$; bunu daha önce de görmüştük. Oyun tek sayılı katlarda bitemez, çünkü tek sayılı katlarda 0 yok. Oyun ancak çift sayılı katlarda bitebilir. Dördüncü katta bir tek 0 var. Dolayısıyla oyunun dördüncü katta (yani üçüncü atışta) bitme olasılığı $1 / 2^{3}$. Altıncı katta iki tane 0 var. Her sıfır için olasılık $1 / 2^{5}$, dolayısıyla oyunun altıncı katta bitme olasılığı $2 / 2^{5}$. Sekizinci katta beş tane 0 var. Her sıfır için olasılık $1 / 2^{7}$, dolayısıyla oyunun sekizinci katta bitme olasılığı $5 / 2^{7}$.
Genel olarak oyunun $2 n$’yinci katta bitme olasılığı $$\frac{p_{2 n}(0)}{2^{2 n-1}}.$$
Demek ki oyunun $2 n$’yinci katta ve daha önce bitme olasılığı böyle sayıların toplamı olan $$ \frac{p_{2}(0)}{2}+\frac{p_{4}(0)}{2^{3}}+\cdots+\frac{p_{2 n}(0)}{2^{2 n-1}}=\sum_{k=1}^{n} \frac{p_{2 k}(0)}{2^{2 k-1}} $$ dir. Dolayısıyla oyunun sonlu bir aşamada bitme olasılığını bulmak için yukarıdaki eşitlikte $n=\infty$ almak gerekiyor, yani $n$’yi sonsuza götürmek. Demek ki oyunun sonlu bir aşamada bitme olasılığı $$\sum_{k=1}^{\infty} \frac{p_{2 k}(0)}{2^{2 k-1}}=1 \tag{4}$$ dir. Biz bu sayının 1 olduğunu önceden biliyoruz. $p_{2 k}(0)$ sayıları kaçtır? Bu sayıların bir formülünü bulsak ve bu formülü $(4)$ eşitliğine yerleştirsek, $(4)$ eşitliği ilginç bir eşitlik olur mu? Evet, olur! $p_{2 k}(0)$ sayılarını bulalım. $p_{2 n}(0)$ sayılarını bulmak için, her $0 \leq k \leq n$ için, $p_{2 n}(2 k)$ sayısını bulmalıyız. Yukarıdaki tablodaki tek sayılı sıraları ve sütunları atalım ki dikkatimizi $p_{2 n}(2 k)$ sayılarına tam olarak verebilelim:
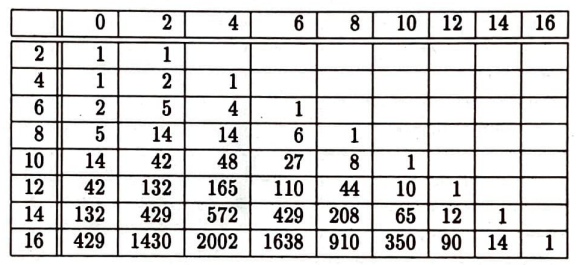
Yukarıdaki tabloya uzun süre, ama oldukça uzun bir süre bakarsanız, $p_{2 n}(2 k)$ saylarını tahmin edebilirsiniz: Eğer $n>1$ ise
$$p_{2 n}(0)=\frac{1}{n}\left(\begin{array}{c}
2 n-2 \\ n-1
\end{array}\right), \tag{5}$$
ve $1 \leq k \leq n$ ise
$$ p_{2 n}(2 k)=\frac{k}{n}\left(\begin{array}{c}
2 n \\ n-k
\end{array}\right) \text {. } \tag{6} $$
Bu formüller sihirbazın şapkasından çıkan tavşanlar gibi sunuldu, ama okur bana inanmak zorunda değil, bu formüllerin doğruluğunu, $(1)$, $(2)$, $(3)$ formüllerini kullanarak, $n$ üzerinde tümevarımla kanıtlayabilir. Yukarıda bulduğumuz $(5)$ eşitliğini $(4)$ eşitliğine yerleştirelim; elde ettiğimiz eşitlikle biraz oynayacak olursak,
$$
\sum_{k=1}^{\infty} \frac{\binom{2k}{k}}{(k+1) 4^{k}}=1 \tag{7}
$$
eşitliğini buluruz. Güzel bir eşitlik.
$^1$ Soruyu bu genel biçimiyle soran ve yanıtlayan Prof. Dr. Nazif Tepedelenlioğlu’na teşekkür ederim.
$^{2}$ Bu formülü nasıl bulduğumuzu okur merak edebilir. Daha önceki önsavda $p_{s}(n)=n p_{s}(1)$ eşitliğini tahmin etmek oldukça kolaydı. Bu önsavdaki formülü bulabilmek için biraz lineer cebir bilmek gerekebilir. Ama formül bulunduktan sonra kanıtlaması oldukça kolaydır.
${ }^{3}$ Bir önceki sırada 0 varsa, oyun orada bitmiştir.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

