Yazar: Ali Nesin
Yıl: 1994 – 3
Sayı: 18
350 yıllık bir arayıştan sonra ünlü Fransız matematikçisi Pierre de Fermat’nın (1601-1665) bir kitabının kenarına not alarak kanıtladığını yazdığı, ancak kanıtını hiç bir zaman kağıda geçirmediği bir teoremin, geçen yaz Haziran’ın sonuna doğru Andrew Wiles adlı bir matematikçi tarafından kanıtlandığını duymuşsunuzdur. Fermat genellikle kanıtladığı teoremlerin kanıtlarını yazmazdı. Söz konusu teorem dışında, Fermat’nın kanıtladığını iddia ettiği bütün teoremler (daha doğrusu önermeler) kendisinden sonra gelen matematikçiler tarafından kanıtlanmıştır. Bu yüzden kanıtı daha yeni bulunan söz konusu önerme “Fermat’nın Son Teoremi” diye anılır. İşte önerme:
Fermat’nın Son Teoremi. Eğer $n \geq 3$ bir tamsayıysa, $x^n + y^n = z^n$ denkleminin pozitif tamsayılarda çözümü yoktur.
Pierre de Fermat’nın bu teoremi gerçekten kanıtlayıp kanıtlamadığını bilmiyoruz. Büyük bir olasılıkla hiç bir zaman da bilemeyeceğiz. Fermat’nın bir kanıta sahip olduğunu düşündüğünden pek kuşku duyan yok. Ancak kanıtının yanlış olduğunu düşünen de çok. Gerçekten de, Fermat’nın çağın ünlü matematikçilerine yazdığı mektuplarda bu önermeden hiç söz etmemesi, kanıtın yanlış olduğunu kendisinin de anlamış olduğu doğrultusunda.
Bu yazının amacı, yukarıdaki teoremle ilgili Fermat’nın bildiğinden emin olduğumuz iki teoremin kanıtını vermek.
Önce $x^2+y^2=z^2$ denklemini ele alalım. Fermat’nın teoremi bu denklemin çözümünün olmadığını söylemiyor. Nitekim denklemin çözümü var. Örneğin,
\[ 9144^2 + 14833^2 = 17425^2. \]
Nasıl buldum bu eşitliği? İşte matematiğin güzelliği burada. Hesaplamaya gerek kalmadan, bu ve bunun gibi bütün eşitlikleri elde edebiliriz. $x^2+y^2=z^2$ denklemini sağlayan daha küçük sayılar da vardır:
\[ 3^2 + 4^2 = 5^2 \]
\[ 5^2 + 12^2 = 13^2 \]
\[ 7^2 + 24^2 = 25^2 \]
\[ 8^2 + 15^2 = 17^2. \]
Babilliler bu eşitlikleri biliyorlardı. M.Ö. 1900 – 1600 yılları arasında kazıldığı anlaşılan bir Babil taş tabletinde bunlar gibi onbeş eşitlik vardır. Babilliler büyük olasılıkla
\[ (2pq)^2 + (p^2-q^2)^2 = (p^2+q^2)^2 \]
eşitliğini de biliyorlardı. Bu eşitlikle $p$ ve $q$ yerine iki tamsayı koyarsak, $x^2+y^2=z^2$ denklemini sağlayan tamsayılar buluruz. Örneğin, $p=127$ ve $q=36$ olarak aldığımızda, yukarıdaki $9144^2 + 14833^2 = 17425^2$ eşitliğini buluruz.
$x^2+y^2=z^2$ eşitliğini sağlayan tamsayılara Pisagor üçlüleri adı verilir. Çünkü, Pisagor’un ünlü teoremine göre, bir dik üçgenin dik açısını oluşturan iki kenarın karelerinin toplamı, üçüncü kenarın karesine eşittir.
Her Pisagor üçlüsü, üç kenarı da tamsayı uzunluğunda olan bir dik üçgen verir. Bunun tersi de doğrudur: üç kenarı da tamsayı uzunluğunda olan her dik üçgen bir Pisagor üçlüsü verir.
$x^2+y^2=z^2$ eşitliğini sağlayan tüm tamsayılar, yani tüm Pisagor üçlüleri bulunabilir mi? Evet. Eski Yunanlı Öklit M.Ö. 300 yılında aşağıdaki teoremi kanıtlamıştır.
Teorem 1. Gerekirse $x$’le $y$’nin yerlerini değiştirirsek,
\[ x^2+y^2=z^2 \]
denkleminin tüm çözümleri şöyle elde edilir: öyle $p,q,d$ tamsayıları vardır ki
\[ x=2dpq, \quad y=d(p^2-q^2), \quad z=d(p^2+q^2) \]
dir.
Birazdan kanıtlayacağımız bu teoremin ışığında, $x^2+y^2=z^2$ eşitliğini sağlayan tüm tamsayıları bulabiliriz. Birkaçını bulalım (hep $d=1$ alacağız).
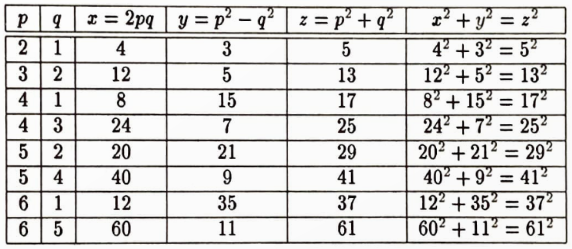
Yukarıda, ortak bölenleri olmayan ve biri çift olan $p$ ve $q$ tamsayılarını aldık yalnızca.
Şimdi $x^4+y^4=z^4$ denklemine gelelim. Bu denklemin pozitif tamsayılarda çözümü olmadığını Fermat kanıtlamıştır. Kanıtta, birinci teorem ve Fermat’ın kendi buluşu olan “sonsuz iniş” adı verilen yöntem kullanılmıştır. Aslında Fermat daha genel bir teorem kanıtlamıştır:
Teorem 2. $x^4+y^4=z^2$ denkleminin, dolayısıyla $x^4+y^4=z^4$ denkleminin de, pozitif tamsayılarda çözümü yoktur.
İkinci teoremin ilginç bir uygulaması vardır. Fermat’nın son teoremi salt 4 için değil, dörde bölünen tüm tamsayılar için doğrudur. Örneğin, $(a, b, c)$ tamsayıları, $x^8+y^8=z^8$ denkleminin bir çözümü olsaydı, $(a^2,b^2,c^2)$ tamsayıları, $x^4+y^4=z^4$ denkleminin bir çözümü olurdu. Oysa ikinci teorem bu son denklemin çözümünün olmadığını söylüyor. Demek ki $x^8+y^8=z^8$ denkleminin de çözümü yoktur. Aynı türden bir akıl yürütme, Fermat’nın teoremini asal $n$ sayıları için kanıtlamanın yeterli olduğunu gösterir. İkiden büyük ilk asal sayı 3. Fermat, teoremi $n=3$ için kanıtladığını mektuplarında sık sık yazmıştır, ama her zaman yaptığı gibi, kanıtını açıklamamıştır. Yıllar sonra, İsviçreli matematikçi Euler (1707 – 1783) $n=3$ için bir kanıt bulduğunu matematikçi Goldbach’a yazmıştır; kanıtın $n=4$ şıkkının kanıtından çok değişik oloduğuna dikkati çekip, yakın gelecekte genel teoremin kanıtlanacağını sanmadığını da eklemiştir. Euler’in 1770 yılında yayımladığı kanıtında açıklamadığı, karanlık kalmış yerler vardı. Bu açıklanmayan yerlerin doğruluğunu büyük matematikçi olan Euler’in bilip bilmediği tartışma konusu. Konuyla ilgili okuduğum kitaplardan, Euler’in düşüncelerinin doğru olduğu, ancak her nedense her tümcesini açıklamadığı izlenimini edindim. Bu kanıt da “sonsuz iniş” yöntemini kullanır. “Sonsuz iniş” yöntemi dışında,
\[ \{\ a+b\sqrt{-3} : a, b \textrm{tamsayılar} \} \]
karmaşık sayılar kümesindeki küpleri bilmek gerekir. Fermat bu kanıtı o çağda bilebilir miydi? Kanıtın Fermat’nın çağının çok ilerisinde olduğu bir gerçek. Ama Fermat da çağının çok ilerisindeydi. Yanıt bilinmiyor.
Yazının kalan bölümünde yukarıdaki iki teoremin kanıtını vereceğiz.
Teorem 1’in Birinci Kanıtı. Eğer $(a, b, c)$, (1) eşitliğini sağlayan üç tamsayıysa, $(ad, bd, cd)$ sayıları da aynı denklemi sağlar. Örneğin, $(8, 15, 17)$ bir çözümdür, bu çözümü ikiyle çarpacak olursak $(16, 30, 34)$ çözümünü buluruz. Yani, bir çözümün çarpımlarını alarak yeni çözümler elde edebiliriz. Bunun tersini de yapabiliriz. Eğer $(a, b, c)$ bir çözümse, ve $d$ tamsayısı $a, b$ ve $c$’yi bölüyorsa, $(a/d, b/d, c/d)$ tamsayıları da bir çözümdür. Dolayısıyla, ortak bölenleri olmayan çözümleri bulmak tüm çözümleri bulmak için yeterlidir. Bundan böyle, $(a, b, c)$ ortak böleni olmayan bir çözümü simgeleyecek. $a^2+b^2=c^2$ olduğundan, $a, b, c$ sayılarından ikisi bir sayıya bölünüyorsa üçüncüsü de aynı sayıya bölünür. Demek ki, $a,b,c$ sayılarından ikisi aynı sayıya bölünemezler. Dolayısıyla bu sayılardan ikisi birden çift olamazlar, yani bu üç sayıdan en az iki tanesi tek sayıdır. Bu sayılardan ikisi tekse üçüncüsü çift olmak zorundadır. Hangi sayı çifttir? $c$ çift olamaz, çünkü $c$ çiftse, $a$ ve $b$ tek sayılardır, dolayısıyla $a^2+b^2$ dörde bölünmez; öte yandan $c^2$ dörde bölünür. Demek ki $a$ ve $b$ sayılarından biri çift. Gerekiyorsa $a$ ve $b$ sayılarının yerimi değiştirerek, $a$ sayısının çift olduğunu varsayabiliriz. Bundan böyle $a$ sayısının çift olduğunu varsayacağız. Demek ki $b$ ve $c$ tel sayılar, ve dolayısıyla $c-b$ ve $c+b$ çift sayılar. O halde
\[ a=2n, \quad c-b=2v, \quad c+b=2w \]
olarak yazabiliriz. (2) eşitliklerinden,
\[ b=\frac{(c+b)-(c-b)}{2}=\frac{2w-2v}{2}=w-v \]
\[ b=\frac{(c+b)+(c-b)}{2}=\frac{2w+2v}{2}=w+v \]
eşitlikleri çıktığından, $v$ ve $w$ sayılarının ortak böleni yoktur, çünkü hem $v$’yi, hem $w$’yi bölen bir sayı, $b$ ve $c$
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 3. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Teoman Yalçınkaya’ya ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

