Yazar: Sinan Sertöz
Yıl: 1994-3
Sayı: 18
Bir kürenin hacmini ilk merak eden kişi kimdi bilemiyoruz , ama bunu ilk hesap etmeye cüret edecek kadar merak eden ilk kişinin Sicilyalı Arşimet olduğunu biliyoruz. Bugün böyle bir hacmi hesaplamak için integral teknikleri kullanıyoruz. Oysa integral hesap Arşimet’den yaklaşık 1900 yıl sonra icat edilecektir. Elektriğin kullanıma girmesine 2100 yıl, penisilinin icadına 2150 yıl, bilgisayar haberleşme ağlarının yayılmasına ise yaklaşık 2200 yıl vardır. Hatta tarihin akışını ve dünyanın siyasini yapısını değiştirecek son iki peygamberden ilkinin doğmasına bile daha birkaç yüzyıl vardır… Roma – Katarca savaşları hala sürmektedir. Nitekim bu savaşlarda taraf tutmak zorunda olan Sicilya krallığı ölümcül bir yanlış yapıp Katarca’nın tarafını tutar. Roma donanmasının uzun süren kuşatmasından sonra Sicilya düşer ve o karışıklıkta bir asker Arşimet’i öldürür. Vasiyeti üzerine mezar taşına silindir içine sokulmuş bir küre çizilir. Çünkü Arşimet’in en çok gurur duyduğu çalışması budur; bir kürenin hacminin, içine tam olarak sığacağı silindirin hacmine oranı. Bu oranı Arşimet üçte iki olarak bulur ve silindirin hacmi bilindiği için kürenin hacmi tam olarak hesaplanmış olur. Arşimet’in mezarı daha sonra kaybolur. Yaklaşık üç yüz yıl sonra Sicilya’da konsül yardımcılığı görevi sırasında Cicero üzerinde bir silindir ve küre şekli bulunan bir mezar taşı bulur… Bugün bu mezar taşı yine kayıp. Meraklı bir turistin Arşimet’in mezarından bir hatıra almak isteyip işin biraz aşırısına kaçtığı sanılıyor.
Arşimet’in bunca gurur ve coşku duyduğu bu hacim hesabı gıpta edilecek sadeliktedir ve mutlaka çağdaşlarına “ben niye akıl edemedim?” dedirtmiştir. Bu konunun matematiksel içeriği dışında bizi ilgilendiren bir başka yönü de bu hesapları içeren Arşimet’in Metotlar adlı eserinin iki bin yıl ortadan kaybolduktan sonra bu yüzyılın başında İstanbul’da ortaya çıkmasıdır.
Arşimet ve eserleriyle ilgili ayrıntılı bir yazıyı daha ileride yazmaya söz verip Arşimet’in kürelerine döneyim. Bulmak istediğimiz hacim yarıçapı r olan bir kürenin hacmi. Özellikle merak ettiğimiz ise tabanının yarıçapı r ve yüksekliği 2r olan silindirin içinde bu kürenin ne oranda yer kapladığı. Bu hesabın bir yerinde Arşimet’in kaldıraçlarının işe karıştığını göreceksiniz, sakın şaşırmayın.
Hacmini hesaplayacağımız küreyi merkezinden geçen bir düzlemle keselim. Elde ettiğimiz çemberi $ABCD$ ile, merkezini $K$ gösterelim (Şekil 1).
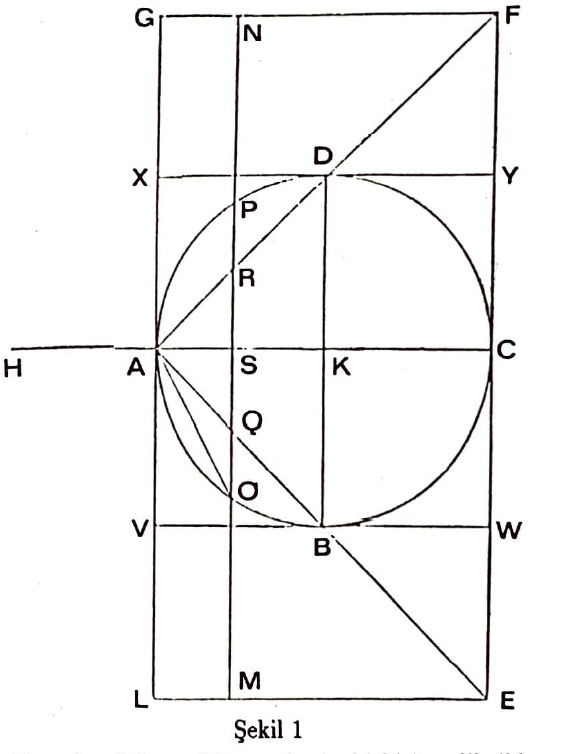
Burada $AC$ ve $BD$ çemberin birbirine dik iki çapı çapı olsun. $C$ noktasından $BD$ doğrusuna bir paralel çizelim ve bu paralel doğrunun $AB$ ve $AD$ doğrultularını kestiği noktalara $E$ ve $F$ diyelim. $E$’den ve $F$’den $EF$ doğrusuna birer dikme çizelim ve bu dikmeler $ABCD$ çemberine $A$ noktasından çizilen teğeti $L$ ve $G$ noktalarında kessinler. $B$ ve $D$ noktalarından çembere çizilen teğetler de $LG$’yi $V$ ve $X$ noktalarında, $EF$’yi de $W$ ve $Y$ noktalarında kessinler. $AEF$ üçgenini $AC$ ekseni etrafında döndürerek bir koni elde ettiğimizi düşüneceğiz. Aynı eksen etrafında bir de $LEFG$ dikdörtgenini döndürüp bir silindir elde edeceğiz. İşte hacimlerini kıyaslamak istediğimiz cisimler hazır. Kürenin hacmi ile koninin hacmini toplayıp silindirin hacminin yarısı olduğunu göreceğiz.
$AC$ ekseni üzerinde rasgele bir $S$ noktası alalım. Bu noktada $AC$ doğrusuna dik olan bir düzlem düşünelim. Bu düzlem, küremizi çapı $OP$ olan bir daire boyunca keser. Aynı düzlem, konimizi çapı $QR$ ve silindirimizi de çapı $MN$ olan daireler boyunca keser. Planımız, $S$ noktasında elde edilen bu dairelerin alanları arasında bir bağıntı bulmak. Daha sonra $S$ noktasını $AC$ boyunca gezdireceğiz. Bu yaptığımızın alalade bir Riemann integrali olduğunu düşünüp burun kıvırmadan önce Arşimetin’in milattan önce üçüncü yüzyılda, Riemann’ın ise milattan sonra on dokuzuncu yüzyılda yaşamış olduklarını hatırlayın…
Artık planladığımız alan kıyaslamasına başlayabiliriz. $MS = AC$ ve $SQ = AS$ olduğundan hemen $MS \cdot SQ = AC \cdot AS$ olduğundan hemen $MS \cdot SQ = AC \cdot AS$ buluruz. $AC$ bir çap olduğu için $AOC$ üçgeni diktir. Diğer açılarına baktığımız zaman bu üçgenin $AOS$ üçgenine benzer olduğunu görürüz. Benzer üçgen bağıntılarından $AC \cdot AS = AO^2$ buluruz. Oysa $AOS$ üçgeninde Pisagor bağıntısı bize $AO^2 = AS^2 + OS^2$ verir. Öte yandan $ACE$ üçgeninin ikizkenar olduğunu ve $SQ$ uzunluğuna eşit olduğunu görürüz. Bütün bunları yerine koyarsak önemli bir bağıntı bulacağız: $MS \cdot SQ = OS^2 + SQ^2$. Bu bağıntının önemini kavramak için biraz ara verip ne yapmakta olduğumuzu hatırlayalım. Elimizdeki cisimleri $AC$’ye dik bir düzlemle kesmiştik. Bu düzlem küremizi yarıçapı $OS$ olan bir daire boyunca, konimizi de yarıçapı $SQ$ olan bir daire boyunca kesmişti. İşte bulduğumuz bu bağıntının sağ tarafı bu dairelerin yarıçaplarının karelerinin toplamı. Bir de bunu $\pi$ ile çarparsanız…
$CA$ doğrusunu $CA = AH$ olacak şekilde $H$ noktasına kadar uzatın. $HC$ doğrusunu $A$ noktasında dayanağı olan bir kaldıraç gibi düşüneceğiz! Bu kaldıracın $H$ ve $S$ noktalarına bazı “ağırlıklar” asacağımız için $\frac{HA}{AS} = \frac{MS}{SQ}$ buluruz. Eşitliğin sağ tarafında payı ve paydayı $MS$ ile çarparsak $\frac{HA}{AS} = \frac{MS^2}{MS \cdot SQ}$, yukarıda bulduğumuz önemli bağlantıyı burada kullanırsak
$\frac{HA}{AS} = \frac{\pi \cdot MS^2}{\pi \cdot OS^2 + \pi \cdot SQ^2}$
buluruz. Yine $HAS$ kaldıracına dönelim; $S$ noktasına silindirden gelen daireyi asalım. $H$ noktasına ise küreden gelen daire ile koniden gelen daireyi birlikte asalım. Dengede duracaklarını gösterdik…
$S$ noktasının $AC$ üzerinde $A$’dan $C$’ye giderken bulunduğu her konumda, bizim elde ettiğimiz daireler yukarıdaki bağıntıyı sağlayacak. Yani silindirden gelen daire olduğu yere asılacak, küreden ve koniden gelen daireler ise $H$ noktasına asılacak. Sonunda $LFEG$ silindiri olduğu yerde kalacak ama $ABCD$ küresi ile $AEF$ konisi beraber $H$ noktasına asılacaklar ve $HAC$ kaldıracı bu yükler altında dengede kalacak. Silindirimizin ağırlık merkezi $K$ noktası olduğu için onun da $K$ noktasında asılı olduğunu düşünebiliriz. Özetlersek, $HAK$ kaldıracının $H$ noktasında yarıçapı $r = AK$ olan bir küre ile taban yarıçapı ve yüksekliği $2r$ olan bir koni asılı, $K$ noktasında ise taban yarıçapı ve yüksekliği $2r$ olan bir silindir asılı. Bu sistem $A$ noktası etrafında dengede duruyor.
Arşimet bu noktada silindirin hacminin $8\pi r^3$ olduğunu, koninin hacminin bunun üçte biri olduğunu ve $AK$’nin de $HA$’nın yarısı olduğunu göz önüne alarak kürenin hacmini $\frac{4}{3} \pi r^3$ olarak buluyor. Koninin hacminin silindirin hacminin üçte biri olduğunu nereden bulduğunu sorgulayacak okuyucuya karşı Arşimet’in sağlam bir yanıtı var: Öklit (!), Elemanlar, XII.10.
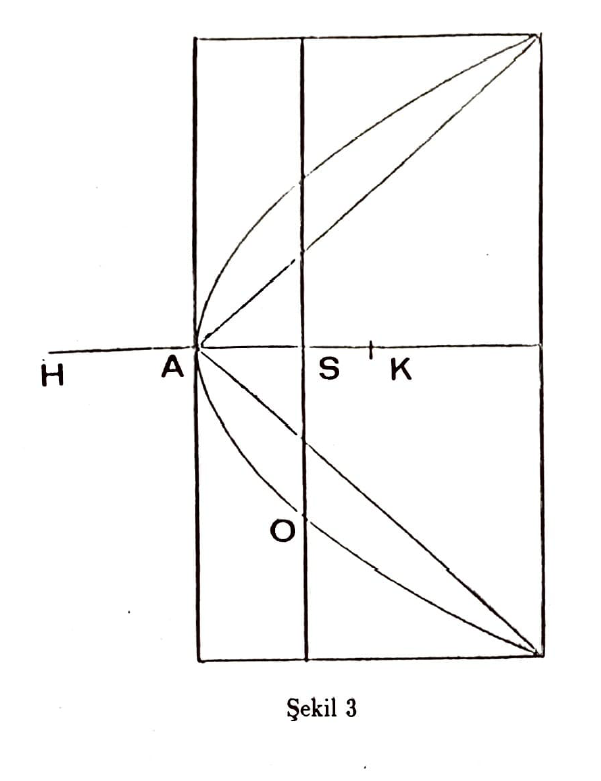
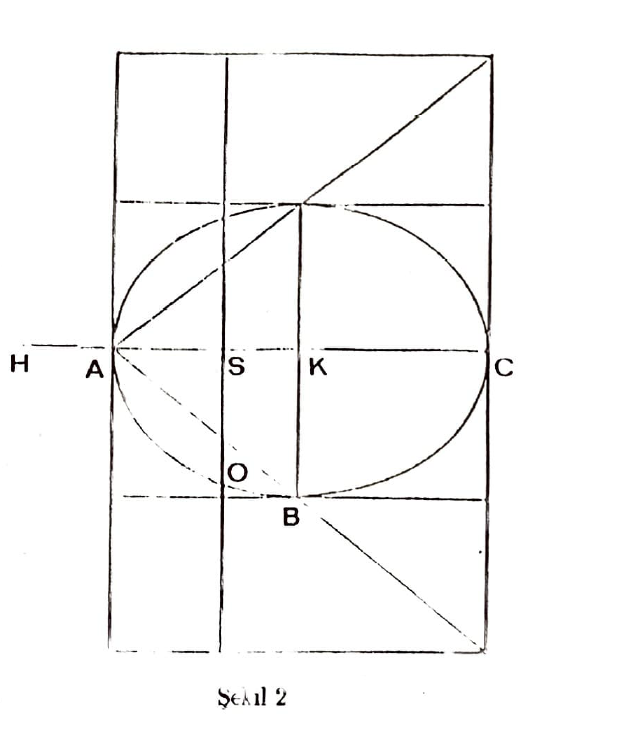
Bu metodun küre üzerinde sonuç vermesinden cesaret alarak Arşimet elipsoidin ve paraboloidin hacimlerini hesaplama problemine de elindeki kaldıraçla girişiyor. Şekil 2 ve 3’te bu çözümler için kullandığı çizimleri görüyorsunuz. Elipsoidin hacmi probleminde $\frac{AS \cdot SC}{SO^2} = \frac{AK^2}{KB^2}$ bağıntısı, paraboloidin hacmi probleminde de $AS = SO^2$ bağıntısı önemli olacak. Hesapların ayrıntılarını vermiyorum. Bu kadar ipucu ve Arşimet’ten yirmi iki yüzyıl kadar sonra yaşıyor olmanın rahatlığıyla nasıl olsa sonucu kendiniz hemen bulabilirsiniz…
Teşekkür. İçinde Arşimet’in bu çalışmasını bulduğum Archimedes, Heath (editör), adlı kitabını bana yıllar önce ödünç veren ve geri istemeyen dostum Prof. Metin Gürses’e gecikmiş teşekkürler.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 3. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep Begüm Kara‘ya ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

