Yazar: Ahmet Şekercioğlu
Yıl: 1994-3
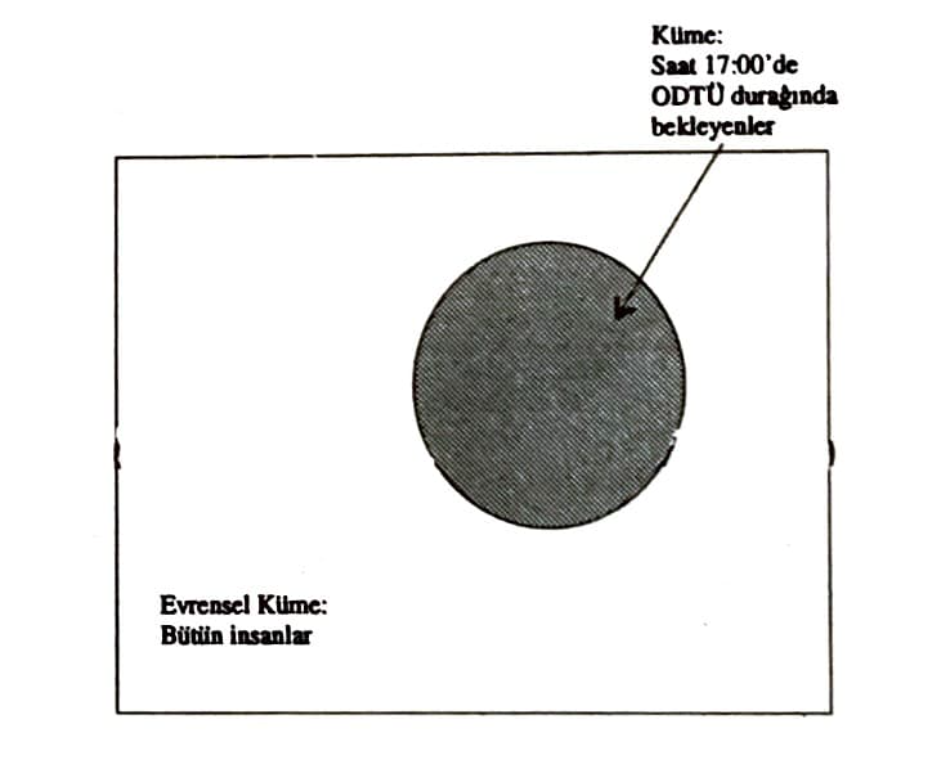
Şimdi diyeceksiniz ki “bulanık kümeler de nereden çıktı?” Fakat “fuzzy” sözcüğüne başka bir karşılık bulamadım bir türlü. Esasında bulanık sözcüğü de bu tür kümeleri tanımlamak için çok da kötü değil gibi geldi bana. Her neyse, önce biraz bu kavramı tanıtmaya çalışayım, sözcüğün tan oturup oturmadığına siz kara verin. Önerilerinizi bekliyorum. Kümeler kuramını anımsamakla başlayalım işe. Küme diye ortak bir isim altın toplanmış nesnelere diyoruz. Örneğin, “saat 17:00’de ODTÜ otobüs durağında bekleyenler” bir küme oluşturuyorlar. Eğer bütün insanların içinde bulunduğu kümeye evrensel küme derse, bu kümeden bir takım insanları ayırıp ortak bir isim altında toplamış ve bir küme yaratmış olduk. Şimdi herhangi bir insanı düşünelim. Bu kişi saat 17:00’de ODTÜ otobüs durağında ya bekliyor, ya da beklemiyor olacaktır, değil mi? Yani yaptığımız tanımlama her bir kişiyi ya ODTÜ otobüs durağında bekleyenler kümesine sokuyor ya da dışında bırakıyor. Kümeleri hayalimizde canlandırmak için çok güzel bir yöntem var: Venn şemasını çizmek. Şekil 1’de bir Venn şeması örneği görebilirsiniz. Bir kümeyi belirlemek için iki yöntem kullanabiliriz Birincisi, kümenin elemanlarını isim isim sayıp kümeyi oluşturmak:
Durakta bekleyenler = {Ali, Oya, Işıl}
Bu yöntem ancak sonlu sayıda elemanı olan kümeleri tanımlamakta kullanılabilir doğallıkta. İkinci yöntem ise bir karakteristik fonksiyon tanımlamak. Bu karakteristik fonksiyon bize evrensel kümenin tek tek bütün bireylerinin bir kümenin içine girip girmediğini söyler.
Öyle bir karakteristik fonksiyon tanımlarız ki, eğer bir nesne bir kümenin elemanı ise, o kümeyi tanımlayan karakteristik fonksiyon 1, değilse 0 sonucunu verir. (1 ve 0’ı karakteristik fonksiyonun verdiği ‘doğru’ ve ‘yanlış’ yanıtları olarak da düşünebiliriz.) Yani karakteristik fonksiyon evrensel kümenin her bir elemanını {1,0} kümesine eşler. Örnek olarak karakteristik fonksiyonunu yazarak gerçel sayılar evrensel kümesinin içinde bir küme tanımlamaya çalışalım:
$$ \mu_{[10,20]} = \left \{ \begin{array}{lr} 1 & 10 \leq x \leq 20 \text{ ise;} \\ 0 & x < 10 \text{ veya} & x > 20 \text{ ise.} \\ \end{array} \right. $$
Bu karakteristik fonksiyon bize [10,20] aralığını ve gerçel sayılar evrensel kümesinin bir alt kümesi olarak tanımlar.
Şekil 1’de “saat 17:00’de ODTÜ otobüs durağında bekleyenler” kümesini simgeleyen Venn şemasını görüyorsunuz.
Şu ana kadar işler yolunda gitti. Gelelim şöyle bir küme tanımına: “Saat 17:00’de ODTÜ otobüs durağında bekleyen gençler.” Şimdi durum biraz karıştı. Tamam, 20 yaşındakiler bu kümeye rahatlıkla girerler. Ama 30 yaşındakiler? 40 yaşındakiler? Acaba sınırı nerede bırakacağız? Şöyle bir tanım yapsak: Eğer birisi 35 yaşından küçükse genç, büyükse yaşlı desek? 36 yaşındaki birisi için çok acımasız davranmış olmaz mıyız? İşte bulanık kümeler burada yardımımıza yetişiyor. En kaba tanımıyla söylersek bir bulanık küme, sınırları kesin çizgilerle belirlenmemiş bir küme oluyor. Başka bir deyişle bir bulanık kümeyi oluşturan her bir eleman, kısmen o kümenin üyesi olabiliyor. Yani her bir elemanın bir üyelik derecesi var. Bu durumda eğer genç insanların kümesini oluşturmak istersek, 36 yaşındaki birisi bu kümenin kısmen elemanıdır diyebiliriz. (Böylece o kişiyi de pek üzmemiş oluruz (!)).
Bulanık kümeleri nasıl tanımlayabiliriz? Normal kümelerde olduğu gibi ya elemanlarını tek tek sayarız, ek olarak her bir elemanın üyelik derecesini de belirtiriz.
$$ \text{durakta bekleyen gençler} = \{1.0/Ali, 0.5/Oya, 0.2/Işıl\} $$
Burada, isimlerin yanındaki sayılar bize o kişinin ne kadar ‘genç’ olduğunu, başka bir deyişle, ne kadar “durakta bekleyen gençler” kümesinin elemanı olduğunu gösteriyor. Yukarıdaki örnekte Ali tümüyle ‘genç’, Oya ise ‘yarı yarıya’ genç olarak düşünülmüş.
Bulanık kümeler -“fuzzy sets”- ilk olarak Lotfi Zadef tarafından ortaya atılmış [Zad65]. Zadeh, küme elemanlarının üyelik derecelerini göstermek için $[0.0,1.0]$ aralığındaki gerçel sayıların kullanılmasını önermiş. Eğer bir elemanın üyelik derecesi 1.0 ise tümüyle o kümenin içinde olduğu, 0.0 ise hiç bir şekilde o kümenin bir elemanı olmadığı söylenebilir. Ya da, 0.5 ise yarı yarıya o kümeye aittir diyebiliriz.
Kümeleri betimlemek için kullandığımız karakteristik fonksiyonlara benzer olarak bulank kümeleri ifade etmek icin de karakteristik fonksiyon tanımlayabiliriz. Öyle bir fonksiyon tanımı yaparız ki, bu fonksiyon her bir eleman için bir üyelik derecesi verir bize. Yani karakteristik fonksiyon evrensel kümenin her bir eleman icin 0.0 ile 1.0 arasinda bir gergel say verir. Bunu bir örnekle açmaya çalışalım, yeniden ‘genç’ler kümesi örneğine dönerek, öyle bir fonksiyon tanımlayalım ki, eğer bir kişinin yaşını bu fonksiyona sokarsak, fonksiyon da bize bu kişinin ne kadar ‘genç’ olduğunu söylesin. Böylece “Saat 17:00’de ODTÜ otobüs durağında bekleyen gençler” bulanık kümesini ifade edelim. İşte bir örnek:
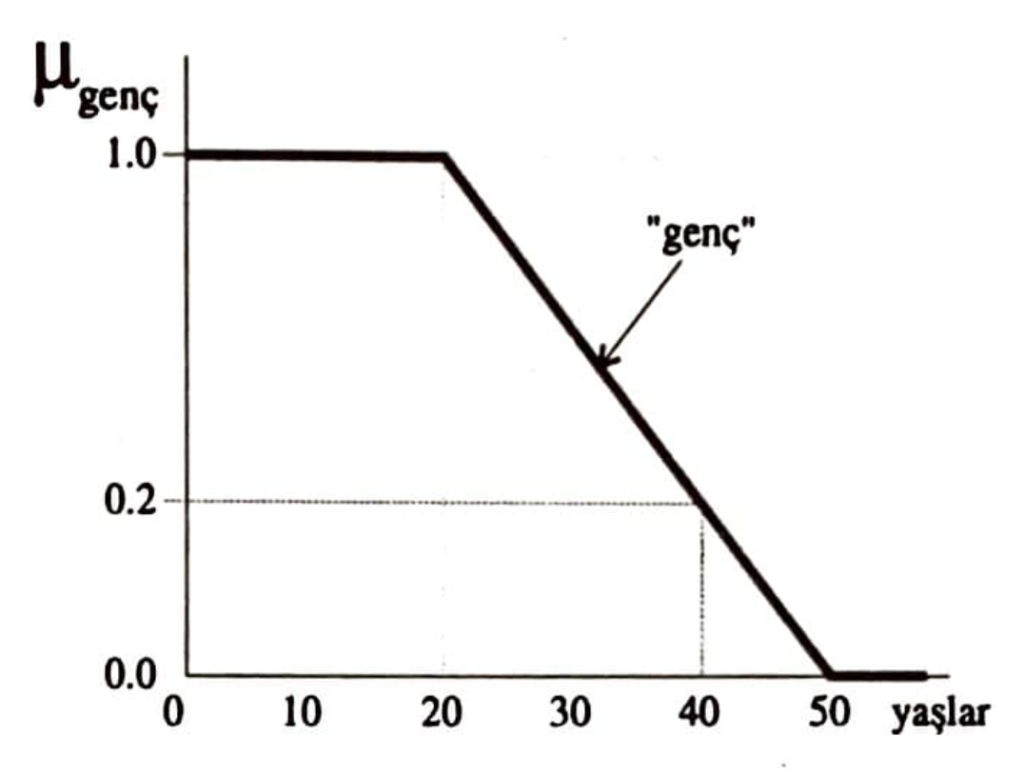
$$ \mu_{genç}(yaş) = \left \{ \begin{array}{lr} 1.0 & \text{eğer yaş} \leq 20 \\ (-0.02 \text{ x} \text{ yaş} + 1) & \text{eğer } 20 > yaş \leq 50 \\ 0.0 & \text{eğer yaş} > 50 \\ \end{array} \right. $$
Şekil 2’de bu örnek karakteristik fonksiyonun grafiğini görebilirsiniz. Şu noktayı da belirtmek gerekir: Bu karakteristik fonksiyon tümüyle benim gençlik tanımımı yansıtmaktadır.
Doğallıkla başka birisi gençliği başka türlü tanımlayacaktır. Yani, her ne kadar “durakta bekleyenler” kümesi tek bir şekilde ifade edilebilirse de “durakta bekleyen gençler” kümesi sonsuz değişik şekilde ifade edilebiliri. Bunu da bulanık kümelerin ilginç özelliği olarak belirteyim. Ayrıca, bulanık kümelerin karakteristik fonksiyonlarına üyelik fonksiyonu -membership function- da denmektedir.
Yeniden şekil 2’ye döner ve burada tanımlanan üyelik fonksiyonunu kullanarak 40 yaşında olan Işıl’ın “durakta bekleyen gençler” bulanık kümesine olan üyelik derecesinin 0.2 olduğunu kolayca görebiliriz.
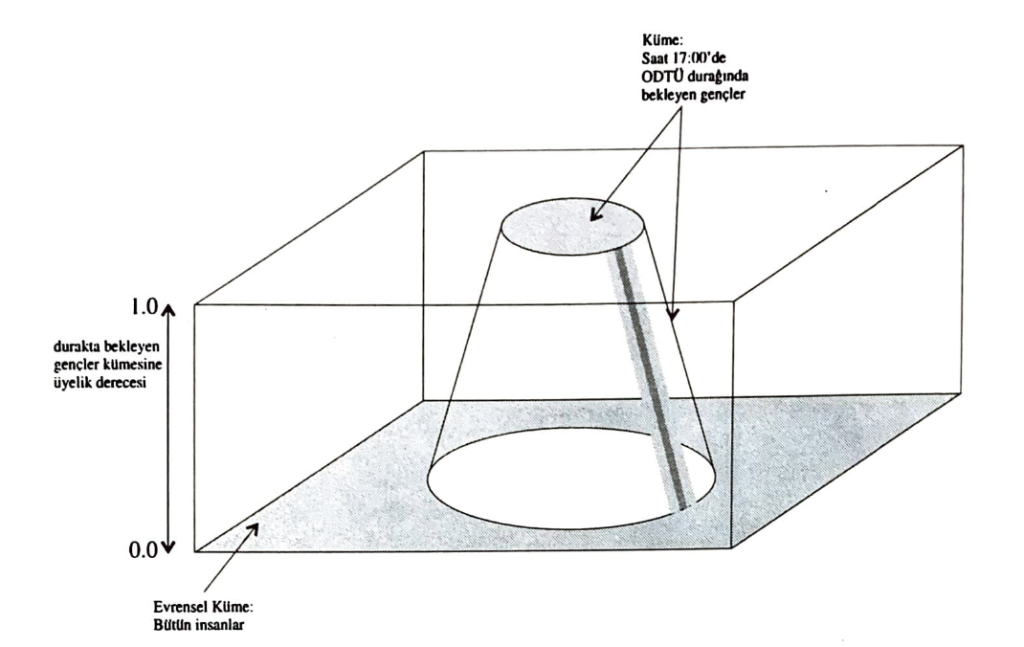
Bulanık kümelerin gösterimi için Venn şemalarını kullanabilir miyiz? Çok doğru olmasa bile şekil 3’deki gibi bir betimleme gözümün önüne geliyor. Bu şekilde, elemanların üyelik derecelerini de belirtmek için üç boyutlu bir Venn şeması çizmeye çalıştım. Şekle fazladan eklenen yükseklik boyutu, her bir elemanın o kümeye olan üyelik derecesini simgeliyor. Bulanık kümenin kesik konum gibi olan biçimi şekil 2’deki üyelik fonksiyonunun yapısından kaynaklanıyor.
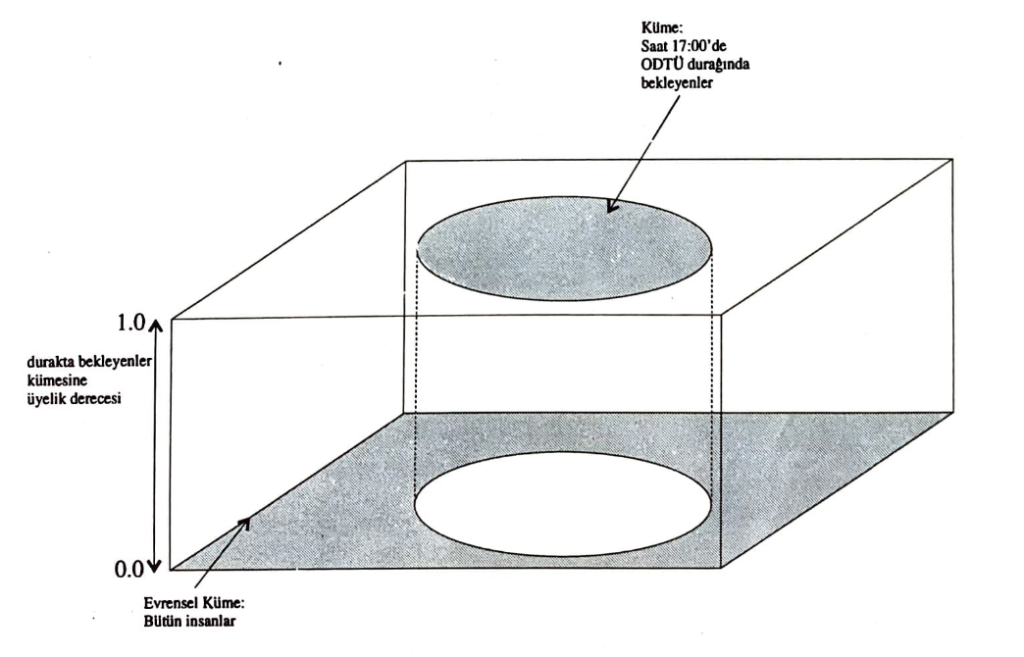
Bu arada, normal kümelerin de aslında elemanlarının üyelik dereceleri 1.0 olan birer bulanık küme olduğunu da belirtmek isterim (Şekil 4). Yani, bulanık kümeler, normal kümeleri de özel bir durum olarak içermekte.
Yeniden klasik kümelerimize dönelim ve kümeler üzerinde yapılan işlemleri anımsayalım biraz. Örneğin, eğer “durakta bekleyenler ve palto giymiş olanlar” kümesinin tanımlamak istersek ne yaparız?
Önce durakta bekleyenler kümesini, sonra palto giymiş olanlar kümesinin oluşturur ve her iki kümede birden olan kişilere bakarız değil mi? Yani bu iki kümenin arakesitini alırız. Bu küme işlemini matematik olarak ifade etmek istersek, eğer “durakta bekleyenler” kümesine $A$, “palto giymiş” olanlar kümesine $B$ dersek, “durakta bekleyenler ve palto giymiş olanlar” kümesi şöyle yazılır:
$$ C = A \cap B $$
ya da
$$ C = {x | x \in A \text{ve} x \in B}$$
“Durakta bekleyenler veya palto giymiş olanlar” kümesi yani bu iki kümenin birleşimi ise
$$ C = A \cup B $$
$$ C = {x | x \in A \text{veya} x \in B}$$
olarak yazılır. Peki, bulanık kümeler dünyasında bu işlemlerin karşılıkları neler olabilir? Bu iki temel bulanık küme işleminin Lotfi Zadeh tarafında verilen matematik tanımları [Zad65] şunlar:
$$ C = A \cap^{f} B $$
ya da
$$ C = \text{min}(\mu_{A}(x),\mu_{B}(x)) $$
ve
$$ C = A \cup^{f} B $$
ya da
$$ C = \text{max}(\mu_{A}(x),\mu_{B}(x)) $$
Burada $\mu_{A}(x)$ ve $\mu_{B}(x)$ $A$ ve $B$ kümelerinin karakteristik fonksiyonlarını temsil ediyorlar. Şimdi yukarıda yazılan bulanık küme işlemlerinin ne anlama geldiğini açmaya çalışalım. “Durakta bekleyen gençler” bulanık kümesinin şekil 2’de gösterdiğimiz karakteristik fonksiyon ile tanımlamıştık. Şimdi bir tane daha bulanık küme tanımlayalım: “Tunus Caddesi boyunca kaldırıma yakın duranlar”. ‘Yakın’ kavramı da bulanık bir kavram. Gündelik hayatta çok kullandığımız halde birisinin bir yere yakınlığının hiç bir zaman metre ile ölçmeyiz değil mi? Aklımızda bir ‘yakın’ kavramı vardır, bunu kullanarak bir şeyin başka bir şeye yakın olup olmadığına karar veririz. Yeniden “Tunus caddesi boyunca kaldırıma yakın duranlar” bulanık kümesine dönersek, bu kümeyi bir karakteristik fonksiyon ile ifade etmeye çalışalım örneğin şekil 5’deki gibi. Eğer “kaldırıma yakın duran” ve “durakta bekleyen gençler” kümesini oluşturmak istersek yukarıda tanımladığımız bulanık arakesiti -fuzzy intersection- işlemini uygularız bu iki bulanık küme üzerinde. Nasıl mı? Bir kişiyi alırız, önce “durakta bekleyen gençler” kümesine olan üyelik derecesini buluruz sonra ikinci kümeyi ziyaret ederiz, o kişinin “kaldırıma yakın duranlar” kümesine olan üyelik derecesini buluruz ve bu iki üyelik derecesinden hangisi daha küçükse o kişinin “kaldırıma yakın duran” ve “durakta bekleyen gençler” kümesine olan üyelik derecesi olarak alırız.
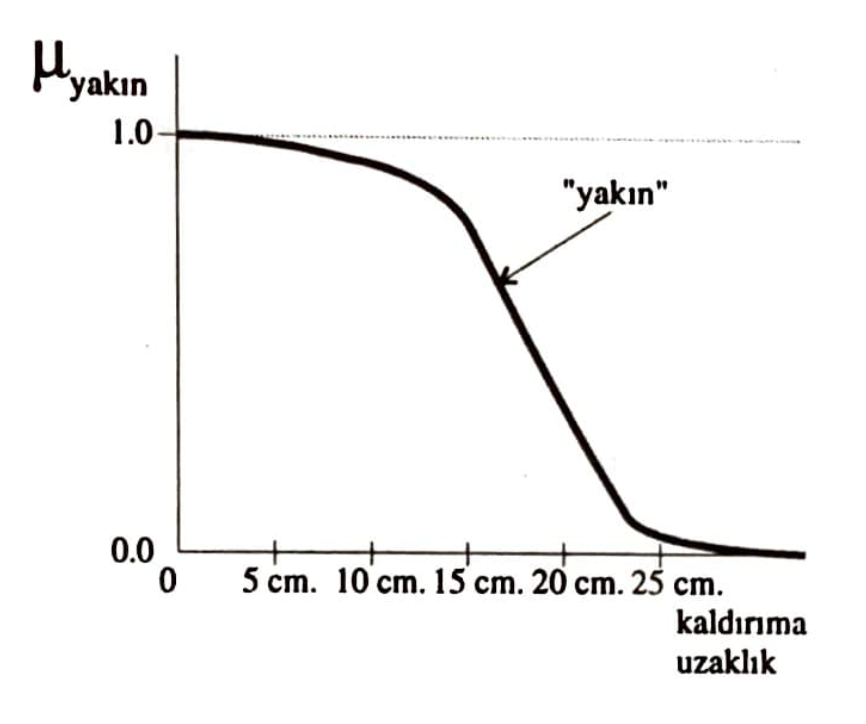
Benzer şekilde, eğer “kaldırıma yakın duran” veya “durakta bekleyen gençler” kümesinin elemanlarının üyelik derecelerini bulmak istersek, bu sefer tek tek üyelik derecelerinin hangisi büyükse onu, o elemanın bulanık-birleşim -fuzzy union- kümesine olan üyelik derecesi olarak alırız.
Bu yazıda bulanık kümeler kuramının temel bir-iki noktasına değinebildim. Nasıl kümeler kuramı matematiğin hemen her alanında etkili olmuşsa, bulanık kümeler de yeni yeni matematiksel kavramlarına doğmasına, araştırma konularının çıkmasına, mühendislik uygulamalarının tasarımlanmasına yol açmıştır. Özellikle yapay zeka alanında ilginç uygulamaların ilk örnekleri gündelik yaşama girmeye başladı bile. Şekil 6 da bulanık kümelerin yarattığı yeni kavramların ve uygulamalardan bazılarını görebilirsiniz. Bu yeni matematik alanın mühendislik ve bilgisayar bilimleri dalındaki uygulamaları şüphesiz ki önümüzdeki yıllarda gündelik hayatımızı daha çok etkileyecek.
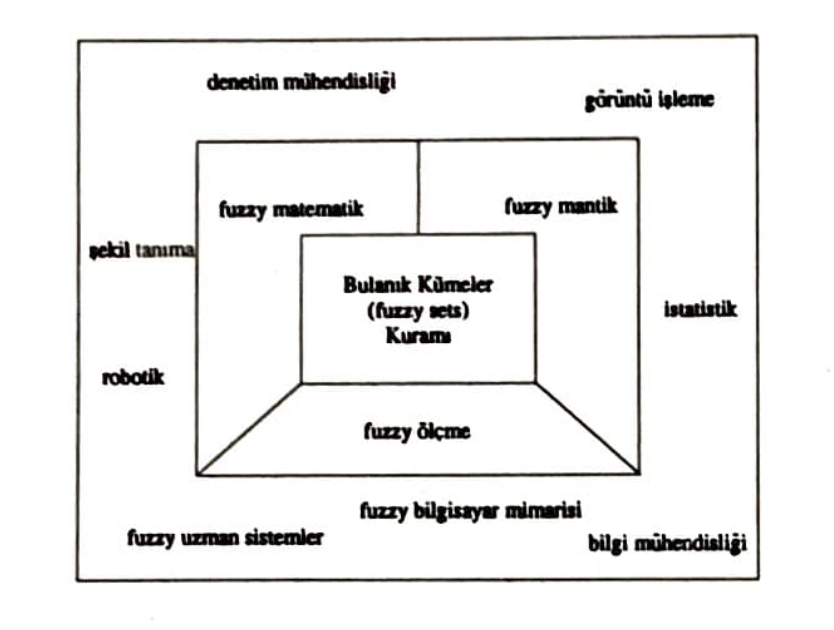
Şekilde bulanık kümeler kuramının yarattığı uygulamalardan bazıları görülüyor. Benimle yazışmak için “yasswin.oz.au” internet adresini ya da “Laboratory of Concurrent Computing Systems, Swinburne Universirt of Technology, P.O. Box 218, Hawthorn, 3122, Avustralya” posta adresini kullanabilirsiniz.
Kaynakça
[Zad65] Lotfi A. Zadeh, Fuzzy Sets, Information and Control, 8, 338-353 (1965).
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Sarper Yurtseven‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

