Yazar: Ali Nesin
Sayı: 1994-2
Bir çizge (graf), sezgisel olarak, noktalardan ve noktaları ikişer ikişer birleştiren (doğru ya da eğri) çizgilerden oluşur. Herhangi iki nokta birleşmek zorunda değildir. Örneğin,
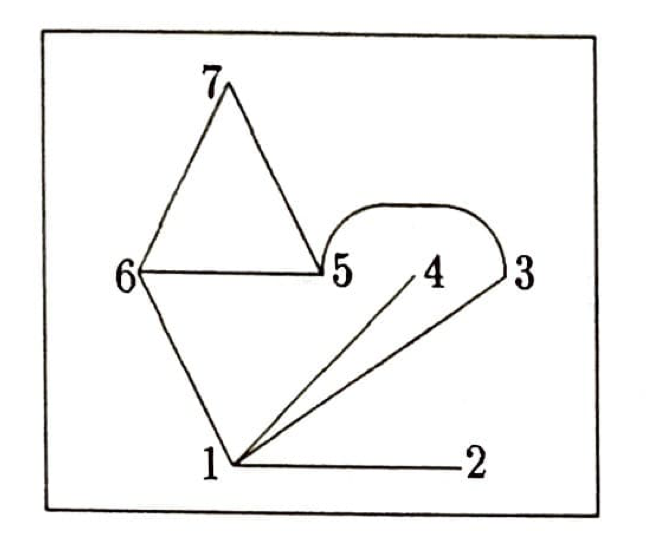
7 noktalı bir çizgedir. Noktalara $1, 2, 3, 4, 5, 6, 7$ adlarını verdik. Birleştirdiğimiz noktalar şunlar:
$$\{1,2\}, \{1,3\}, \{1,4\}, \{1,6\}, \{3,5\}, \{5,6\}, \{5,7\}, \{6,7\}$$
Bu iki öğelik kümelere bağıntı adı da verilir. Noktaları nasıl bir çizgiyle birleştirdiğimiz önemli değil. Hatta çizgiler kesişebilir bile (kesiştikleri yere çizgenin bir noktasını koymayız o zaman). Noktaların yerleri de önemli değil. Okur neyin önemli olduğunu merak edebilir! Önemli olan hangi noktayla hangi nokta arasında çizgi (yada bağıntı) olduğu. Başka bir şey önemli değil. Örneğin, yukarıdaki çizgeyle, aşağıdaki çizgeler aynı çizgelerdir:
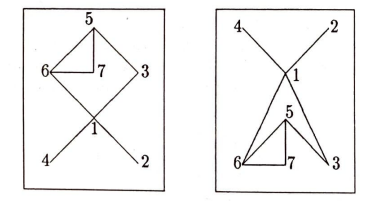
Bu yazıda ilginç olduğu kadar da şaşırtıcı bir teorem kanıtlayacağız. Size sonsuz tane nokta verdim:
$$1, 2, 3, 4, 5, …$$
noktalarını. Bu noktalardan bir çizge yapmanızı istiyorum. Her iki nokta için yazı-tura atacaksınız. Yazı gelirse noktaları birleştireceksiniz, tura gelirse birleştirmeyeceksiniz. Her iki nokta için yazı-tura atmayı bitirdiğinizde (!) noktaların adlarını silin. Hangi noktanın 1 noktası, hangi noktanın 2 noktası olduğu belli olmasın. Elinizde adsız noktalar ve bir takım çizgiler kalacak. Ben de aynı şeyi yapacağım. Sizin çizginize bakmadan…Böylece adsız iki rasgele çizge elde edeceğiz. Sizin rasgele çizgeniz ve benimkisi. Şimdi çizgelerimizi karşılaştıralım. İki çizgenin de aynı olduklarını göreceğiz. Tıpatıp birbirine benziyorlar! Sanki biri öbürünün burnundan düşmüş. İnanılır gibi değil ama doğru! Ne sihirdir ne keramet, matematiktir matematik! Dahası var. Diyelim, ben noktaları birleştirmek için yazı-tura atmadım da zar attım. 6 geldiğinde noktaları birleştirdim, gelmediğinde birleştirmedim. Sizse yazı-tura attınız. Noktaların adlarını adlarını sildiğimizde gene aynı çizgeleri elde ederiz!
‘Çizge‘ kavramının matematiksel tanımıyla başlayalım. N bir küme olsun. B, N‘nin iki öğelik altkümelerinden oluşan bir küme olsun1. Eğer her $x \epsilon N$ için, $(x,x) \notin B$ ise, $(N,B)$ çiftine bir çizge denir2. Yukarıdaki örnekte,
$$N=\{1, 2, 3, 4, 5, 6, 7\}$$
ve
$$B=\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 6\}, \{3, 5\}, \{5, 6\}, \{5, 7\}, \{6,7\}\}$$
olarak tanımlanmıştır. Rasgele çizgeleri tanımlamadan önce az noktalı çizgileri bulalım.
Eğer $N=\{1\}$ ise, yani $N$’de bir nokta varsa, $B$ boşküme olmak zorunda. dolayısıyla $N=\{1\}$ üzerine bir tek çizge kurulabilir. İşte o çizge:

Şimdi de iki noktalı çizgelere bakalım. $N=\{1, 2\}$ olsun. Bu durumda $B$ ya boşkümedir yada $\{\{1, 2\}\}$ kümesidir. Demek ki iki noktalı iki çizge var:
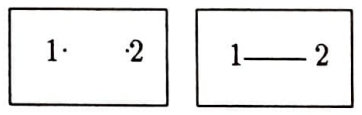
Şimdi amacımız üç noktalı çizgeleri bulmak. Ama bu çizgelerden çok olduğundan, arada unuttuğumuz olmasın diye önce n noktalı kaç tane çizge olduğunu bulalım. n noktalı, $2^\left(\begin{array}{c} n\\2 \end{array} \right)$ tane çizge olduğunu iddia ediyorum, ve hemen kanıtlıyorum: $N$ kümesinin n tane öğesi varsa, $\left(\begin{array}{c} n\\ 2 \end{array} \right)$ tane iki öğelik altkümesi vardır. $B$ iki öğelik altkümelerinden oluştuğundan, $B$ için $2^\left(\begin{array}{c} n\\2 \end{array} \right)$ seçeneğimiz var. Demek ki n noktalı $2^\left(\begin{array}{c} n\\2 \end{array} \right)$ tane çizge vardır. Eğer $n=3$ olarak alırsak, bundan 3 noktalı 8 tane çizge olduğu çıkar. Bu 8 çizgeyi teker teker bulalım. $N=\{1, 2, 3\}$ olsun. İşte 8 çizge:
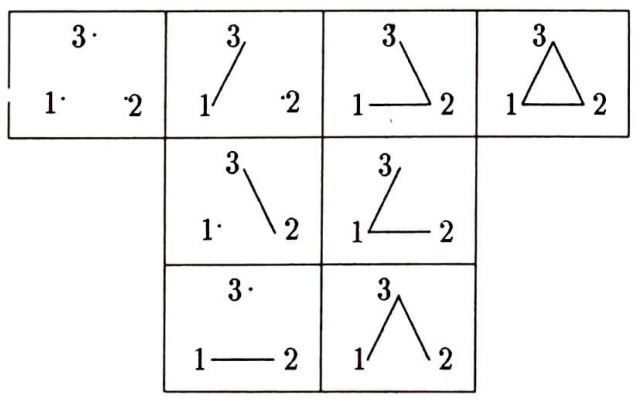
Üç nokta arasındaki bağıntıları yazı-tura atarak karar verecek olursak, yukarıdaki çizgelerden birini elde etme olasılığı $1/8$’dir.
Yukarıdaki çizgelerden noktaların adlarını, yani sayıları silersek, çizge sayımız azalır.
Örneğin, bir bağıntısı olan üç çizgenin noktalarının adları silindiğinde bir çizge olurlar. Bunun gibi, iki bağıntısı olan üç çizgeden de bir adsız çizge elde ederiz. Böylece noktaların adını yazmadığımızda dört çizgemiz kalır:
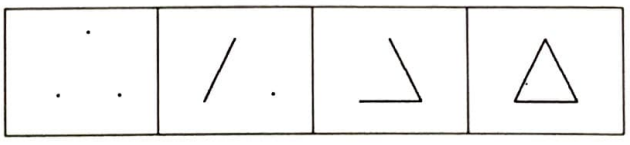
Eğer çizgeyi yazı-tura atarak bulmuşsak, yani her bağıntının olasılığı $1/2$ ise, bu adsız çizgelerin olasılıkları sırasıyla $1/8$, $3/8$, $3/8$ ve $1/8$’dir.
İki çizgenin noktalarının adlarını sildiğimizde aynı çizgeyi elde etmek ne demektir? Bunun matematiksel tanımını bilmek bu yazı için gerekli değildir, bu yazı için sezgiler yeterlidir. Bir örnek daha verelim ki kuşkuya yer kalmasın. Aşağıdaki iki çizgeye bakalım.
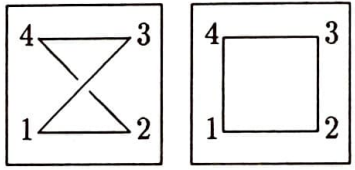
Bu iki çizge birbirlerine çok benzerler. Tek ayrımları noktalarının adlarıdır. Soldaki çizgede 3 ve 4 noktalarının yerlerini değiştirirsek (bağıntılarıyla birlikte) sağdaki çizgeyi buluruz. Yani noktaların adları olmasaydı iki çizge arasında bir ayrım olmayacaktı.
Soldaki çizgenin bağıntıları şunlardır:
$$B=\{\{1, 2\}, \{2, 4\}, \{ 4, 3\}, \{3, 1\}\}.$$
Sağdaki çizgenin bağıntılarıysa,
$$B’=\{\{1, 2\}, \{2, 3\}, \{3, 4\}, \{4, 1\}\}.$$
Şimdi, $f(1)=1$, $f(2)=2$, $f(3)=4$, $f(4)=3$ göndermesini (fonksiyonunu) ele alalım. Bu gönderme, $B$ bağıntılarını $B’$ bağıntılarına gönderiyor. İşte iki çizgenin noktaları silindiğinde aynı çizge bulunması bu demektir3.
Dört noktalı ve adsız çizgeleri bulalım. Bunları bağıntı sayısına göre bulabiliriz: önce hiç bağıntısı olmayanlar, sonra bir bağıntısı olanlar, sonra iki bağıntısı olanlar…
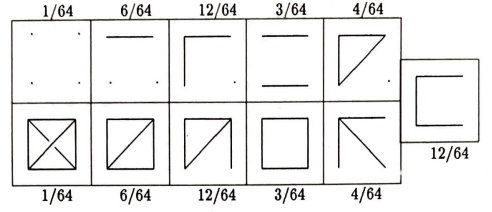
Çizgelere iliştirilen $1/64$, $6/64$, $3/64$ gibi sayılar, bağıntılara karar vermek için yazı-tura atıldığında, çizgenin elde edilme olasılığıdır. Yukarıda yaptığımız hesaplardan, 4 noktalı çizge sayının $2^\left(\begin{array}{c} 4\\2 \end{array} \right) =2^6=64$ olduğunu biliyoruz. Bir bağıntılı çizge sayısı kaçtır? Dört noktadan ikisini seçip aralarına bir bağıntı koymamız gerekiyor. Demek ki $\left(\begin{array}{c} 4\\2 \end{array} \right)$ =6 tane bir bağıntılı çizge var. Dolayısıyla bir bağıntılı çizge elde etme olasılığımız $6/64^4$.
Şimdi sonsuz rasgele çizgelere gelelim. $N$ kümesi
$$1, 2, 3, 4,…$$
gibi pozitif doğal sayılardan oluşan küme olsun. Bunlar noktalarımız. İki nokta arasında bağıntı olup olmadığına karar vermek için yazı-tura atacağız. Böylece bir $B$ bağıntılar kümesi elde edeceğiz. Bu çizgeye $R$ adını verelim ($R$, ‘rasgele’nin $R$’si).
$R$ çizgesi hakkında ne söyleyebiliriz? Rasgele çizge olduğundan hiç birşey bilmemiz olası değil diye düşünebilir okur. İlk bakışta öyle bile görünse, ikinci bakışta $R$ çizgesi üzerine çok şey bildiğimiz anlaşılır. Basit bir örnekle başlayalım.
Rasgele çizgenin herhangi iki nokta arasındaki ”uzaklığın” en fazla iki olduğunu kanıtlayayım; yani bir noktadan bir başka noktaya gidebilmek için üçuncü bir noktadan geçilerek gidilebileceğini kanıtlayayım. $R$ rasgele çizgesinde rasgele iki nokta alalım; diyelim 1 ve 2 noktalarını. Savım şu: öyle bir üçüncü nokta vardır ki, bu üçüncü nokta hem 1 noktasıyla, hem de 2 noktasıyla bağıntılıdır. Savımı kanıtlayayım. 3 noktasını ele alalım. Eğer şanslı bir günümdeysem, 3 noktası dilediğim gibi bir noktadır, yani hem 1 noktasıyla, hem de 2 noktasıyla bağıntılıdır. Bunun böyle olma olasılığı $1/4$. Demek ki $1/4$ olasılıkla 3 noktası varlığını iddia ettiğim noktalardan biri olacak. Öte yandan $3/4$ olasılıkla 3 noktası istediğim gibi bir nokta olmayacak. Şimdi 3 ve 4 noktasını ele alalım. Bu iki noktadan hiçbirinin dilediğim gibi bir nokta olmama olasılığı $(3/4)^2$. Eğer n tane nokta alırsak, bu n noktadan hiçbirinin dilediğim gibi bir nokta olmama olasılığı $(3/4)^n$; en az bir tanesinin dilediğim gibi bir nokta olma olasılığıysa $1-(3/4)^n$. Ama n büyüdükçe $(3/4)^n$ azalıyor, sıfıra yaklaşıyor. Dolayısıyla $1-(3/4)^n$ sayısı bire yaklaşıyor. Demek ki, $3, 4, 5, 6,…$ noktalarından hiçbirinin benim istediğim gibi bir nokta olmama olasılığı
$$\lim_{n \to \infty} (\frac{3}{4})^n=0$$
ve en az birinin benim istediğim gibi bir nokta olma olasılığı
$$\lim_{n \to \infty} (1-(\frac{3}{4})^n)=1.$$
Demek ki 1 olasılıkla dilediğim gibi bir nokta vardır.
Rasgele çizgiler üzerine bir başka sonuç daha çıkaralım. $R$, rasgele çizgeniz olsun. Noktaların adlarını silin. Sonra rasgele bir sonlu çizge alın, örneğin yazının en başında örnek olarak sunduğumuz 7 noktalı çizgeyi. Onun da adlarını silin. Bu adsız ve sonlu çizgeye $S$ adını verelim. $S$ sonlu çizgesi, rasgele çizgenizin bir altçizgesidir, yani $R$ çizgesinin içinde bulabilirsiniz $S$ çizgesini. Neden? Şu nedenle: Rasgele çizgenizin noktalarını yedişer yedişer ayırın.
Örneğin şöyle (noktaların adlarını silmiştik; aşağıdaki sayılar noktaların adları değil; yalnızca birbirinden değişik noktalar olduğunu vurgulamak için kullanıyoruz bu sayıları):
$$R_1=\{1, 2,…, 7\}$$
$$R_2=\{8, 9,…, 14\}$$
$$.$$
$$.$$
$$.$$
$$R_n=\{7n+1, 7n+2,…, 7n+7\}$$
$R_1$ altçizgisine bakalım. Bu çizgenin $S$ çizgesi olma olasılığı en az $1/2^\left(\begin{array}{c} 7\\2 \end{array}\right)$, olmama olasılığıysa en çok $1-1/2^\left(\begin{array}{c} 7\\2 \end{array}\right)$. Bu olasılığa $a$ adını verelim.
$$0<a\leq 1-(\frac{1}{2})^\left(\begin{array}{c} 7\\2 \end{array}\right)<1$$
eşitsizliklerine dikkatinizi çekerim. $R_1$ çizgesinın $S$ çizgesi olmama olasılığı $a$. $R_1$ ve $R_2$ çizgelerinden hiçbirinin $S$ çizgesi olmama olasılığıysa $a^2$. Genel olarak, $R_1,…, R_n$ çizgelerinden hiçbirinin $S$ çizgesi olmama olasılığı $a^n$; en az birinin $S$ olma olasılığıysa $1-a^n$. $a$, 1’den küçük olduğundan, $a^n$ sayıları gittikçe küçülür, sıfıra yaklaşır. Dolayısıyla $1-a^n$ bire yaklaşır. Sonsuz tane $R_n$ çizgesi olduğundan, bunlardan birinin $S$ olma olasılığı 1’dir. Dolayısıyla, $R$ çizgesinde $S$’e tıpatıp benzeyen bir altçizge (1 olasılıkla, yani yüzde yüz) vardır.
Son olarak yazının başında iddia ettiğım savı kanıtlayayım. Sizin elinizde rasgele bir çizge var. Bu çizgeye $R=(N,B)$ diyelim, noktalarınız da
$$a_1, a_2, a_3,…$$
olsun. Benim çizgeye $R’=(N,B’)$ diyelim. Noktalarım
$$a’_1, a’_2, a’_3, …$$
olsun. Bu iki çizgenin noktalarının adlarını değiştireceğim. $a$ ve $a’$ noktalarını $b$ ve $b’$ yapacağım, ve bu işi öyle yapacağım ki, noktaların adlarını sildiğimizde iki çizgenin birbirinin aynısı olduğu apaçık belli olacak. Bağıntılara dokunmayacağım. Yalnızca eski adları silip yeni adlar koyacağım yerine, sonradan bu yeni adları da sileceğim.
Adına ”gelgit yöntemi” denilen kullanacağım yöntem matematikte az bilinir.
Birinci Adım. $R$ çizgesinde başlayalım işe. $a_1$ noktasına $b_1$ diyelim bundan böyle. $R’$ çizgesinds $b_1$’e benzeyen bir nokta bulabilir miyiz? Elbette! Herhangi bir nokta $b_1$’e benzer.
Örneğin $a’_1$ noktası. Bundan böyle $a’_1$ noktasına $b’_1$ adını verelim. Çizgelerimizin noktaları şimdilik şöyle:
$$R: b_1\qquad a_2\qquad a_3\qquad a_4\qquad a_5\qquad …$$
$$R’: b’_1\qquad a’_2\qquad a’_3\qquad a’_4\qquad a’_5\qquad …$$
İkinci Adım. Şimdi $R’$ çizgesine geçelim. $a’_2$ noktasına $b’_2$ adını verelim. Ve $\{b’_1, b’_2\}$ altçizgenine bakalım. $b’_1$ ve $b’_2$ arasında bağıntı olabilir ya da olmayabilir. $R$ çizgesinde öyle bir $a_n$ noktası bulmak istiyorum ki $\{b_1, a_n\}$ çizgesiyle $\{b’_1, b’_2\}$ çizgesi -noktalarının adları dışında- birbirinin aynı olsun.
Diyelim $b’_1$ ve $b’_2$ arasında bir bağıntı var. O zaman, $R$ çizgesinde öyle bir $a_n$ noktası seçmeliyim ki, $a_n$ noktasıyla $b_1$ noktası arasında bağıntı olsun. Böylece bir $a_n$ noktası bulabilir miyim? 1 olasılıkla bulabileceğimi iddia ediyorum. Çünkü $R$ çizgesinin hiç bir noktasında $b_1$ noktasına bağıntılı olmama olasılığı sıfırdır. Bu şöyle anlaşılır. $m$ herhangi bir doğal sayı olsun. $a_2, a_3,…, a_m+2$ noktalarından hiçbirinin $b_1$ noktasıyla bağıntısı olmamasının olasılığı $1/2^m$. Dolayısıyla bu noktalardan en az birinin dilediğim gibi bir nokta olma olasılığı $1-1/2^m$. Sonsuz tane noktamız olduğundan, noktalardan birinin dilediğim gibi bir nokta olma olasılığı
$$\lim_{m \to \infty} (1-\frac{1}{2^m})=1.$$
Dolayısıyla 1 olasılığıyla öyle bir noktam var. Bu nokta $a_2$ olmayabilir, $a_3$ olmayabilir, belki $a_4$ de olmayabilir, ama bir tanesi $b_1$’e bağıntılı olacak. $R$ çizgesinde böyle bir nokta seçelim. Diyelim $a_4$ noktası $b_1$ noktasına bağıntılı. $a_4$ noktasına bundan böyle $b_2$ diyelim. Şimdi $\{b_1, b_2\}$ altçizgesiyle, $\{b’_1, b’_2\}$ altçizgesi -noktalarının adları dışında- birbirinin aynı.
Eğer $b’_1$ ile $b’_2$ arasında bağıntı yoksa, $R$ çizgesinde $b_1$ ile bağıntısı olmayan bir nokta seçilir ve bu noktaya $b_2$ adı verilir.
$a_4$ noktasına $b_2$ adını verdiğimizi varsayarak çizgelerimizin noktalarını yeni adlarıyla sıralayalım:
$$R: b_1\qquad b_2\qquad a_2\qquad a_3\qquad a_5\qquad a_6\qquad a_7\qquad …$$
$$R’: b’_1\qquad b’_2\qquad a’_3\qquad a’_4\qquad a’_5\qquad a’_6\qquad a’_7\qquad …$$
Üçüncü Adım. $R$ çizgesine geri dönelim. $a_2$ noktası adı değiştirilmeyen ilk nokta. Bu noktayı $b_3$ yapalım. $\{b_1, b_2, b_3\}$ altçizgesine bakalım. Diyelim, $b_3$ ile $b_1$ bağıntılı, ama $b_3$ ile $b_2$ bağıntılı değil. $R’$ çizgesinde öyle bir $a’_n$ noktası bulacağız ki $a’_n$ noktası $b’_1$ ile bağıntılı olacak ama $b’_2$ ile bağıntılı olmayacak. Eğer öyle bir $a’_n$ bulabilirsek, $\{b_1, b_2, b_3\}$ altçizgesiyle $\{b’_1, b’_2, a’_n\}$ altçizgesi, noktalarının adları dışında, aynı çizge olacaklar. Böyle bir $a’_n$ noktası bulabilir miyiz? Evet! Biri olmazsa, bir başkası olmak zorunda. Çünkü $a’_3, a’_4,…, a’_m+3$ noktalarından hiçbirinin dilediğimiz gibi bir nokta olmama olasılığı $(3/4)^m$, ve $m$ sonsuza gittiğinde bu olasılık sıfıra gidiyor. Demek ki dilediğimiz gibi bir $a’_n$ noktası bulma olasılığımız 1. Diyelim $a’_6$ noktası işimizi görüyor. $a’_6$ noktasının adı bundan böyle $b’_3$ olsun. Çizgelerimizin noktaları şimdi şöyle:
$$R: b_1\qquad b_2\qquad b3\qquad a_3\qquad a_5\qquad a_6\qquad a_7\qquad …$$
$$R’: b’_1\qquad b’_2\qquad b’_3\qquad a’_3\qquad a’_4\qquad a’_5\qquad a’_7\qquad …$$
Dördüncü Adım. Bu kez $R’$ çizgesinden işe başlayacağız. Adını değiştirmediğimiz ilk nokta $a’_3$. Bu noktaya $b’_4$ adını verelim. Şimdi $R$ çizgesinde öyle bir $a_n$ noktası bulalım ki, $\{b’_1, b’_2, b’_3, b’_4\}$ altçizgesiyle $\{b_1, b_2, b_3, a_n\}$ altçizgesi -noktaların adlarını dikkate almazsak- aynı çizge olsunlar. Öyle bir $a_n$ noktası 1 olasılıkla bulunabilir. Nasıl bulunur? Yukarıdaki gibi. Hiçbir $a_n$ noktasının istediğimiz gibi bir nokta olmaması olasılığı sıfırdır. Demek ki birinin dilediğimiz gibi bir nokta olma olasılığı birdir.
Böylece sürdürürüz. Tek sayılı adımlarda $R$ çizgesinden, çift sayılı adımlarda $R’$ çizgesinden başlarız. Bu yöntemle ne benim çizgemden ne de sizin çizgenizden nokta unutulmaz. Sonsuza dek sürdürdüğümüzde noktalarımız $b$ ve $b’$ harfleriyle yazılmış olur, ve her $n$ için
$$\{b_1,…,b_n\}$$
altçizgesiyle
$$\{b’_1,…,b’_n\}$$
altçizgesi, adları dışında, birbirinin aynısıdır. Dolayısıyla,
$$\{b_1,b_2,b_3,…\}$$
çizgesiyle
$$\{b’_1,b’_2,b’_3,…\}$$
çizgesi arasında -noktalarının adları dışında- hiç ama hiç bir ayrım yoktur.
Ne kanıtladık? Sizin rasgele çizgenızle benim rasgele çizgem birbirinin eşidir. Bir (1) olasılıkla!
*Bilkent Üniversitesi Matematik Bölümü öğretim üyesi
1$N$, ‘nokta’nın N’si $B$ ise ‘bağıntı’nın B’si
2 $(x,x)$ öğesinin $B$’de olmaması, $x$’le $x$ arasında bağıntı olmaması demektir. Bu koşulu kabul etmemizin ciddi hiç bir nedeni yok. ‘Çizge’nin tanımında bu koşulu koşmayan kitaplar var. Bizim bu koşulu kabul etmemizin tek nedeni çizgelerimizin daha basit olmalarını sağlamak. Matematiksel bir gerekçemiz yok.
3Bunu matematiksel olarak ifade edelim: $(N, B)$ ve $(N’, B’)$ iki çizge olsunlar. Eğer $f(B)=B’$ eşitliğini sağlayan ve birebir ve örten olan bir $f: N \longrightarrow N’$ göndermesi varsa, $(N, B)$ ve $(N’, B’)$ çizgelerine eşyapısal çizgeler denir. İki eşyapısal çizgenin birbirinden tek ayrımı noktalarının adlarıdır. Bu çizgelerden birindeki noktaların adları uygun bir biçimde değiştirildiğinde ($x$ noktasına $f(x)$ denildiğinde örneğin), öbür çizge bulunur.
4Yukarıdaki 11 çizge rasgele konulmamıştır. Alt alta gelen çizgeler birbirileriyle ilintilidir. Üst kattan herhangi bir çizgeyi alalım. Bu çizgenin bağıntılarını silelim ve bağıntı olmayan yerlere bağıntı koyalım. Böylece alt kattaki çizgeyi elde ederiz. En sağdaki çizge için aynı şeyi yapacak olursak gene aynı çizge elde edilir. Alt alta gelen iki çizgenin olasılıkları aynıdır. Yazı-tura atıldığında aynıdır. Eğer zar atarak bağıntılara karar verecek olursak olasılıklar değişebilir. Örneğin, zar attığımızda 6 gelirse bağıntı koymaya, gelmezse bağıntı koymamaya karar verecek olursak, çizgenin bağıntı sayısı çoğaldıkça olasılığı azalır.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Burcu Fidan’a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

