Yıl: 1994-1
Yazar: Hüseyin Demir
İlgin bir teoremin geometrik bir ispatını veremediğimizde ya da bir problemin çözümünü geometrik olarak bulamadığmızda yahut istek üzerine doğrudan analitik geometriye başvururuz.
İlgin bir $Oxy$ koordinat sistemi, Öklid düzlemindeki bir $O_0 x_0 y_0$ koordinat sisteminden ilgin dönüşümle elde edilir (Şekil 29).
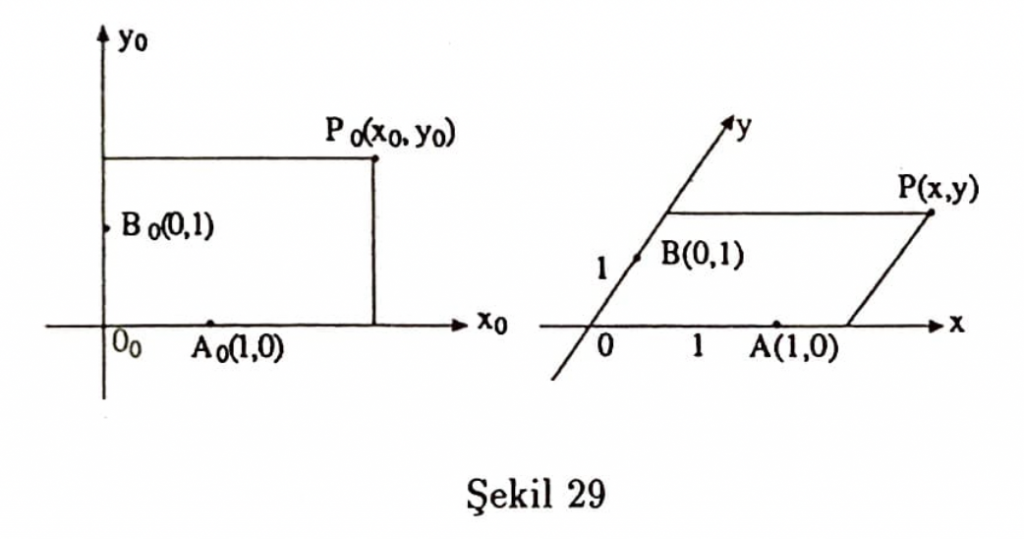
Eksenler üzerinde birim uzunlukları veren $A(1,0), B(0,1)$ noktaları keyfi olarak seçilebilir.
Doğru Denklemi
$P_1(x_1,y_1),P_2(x_2,y_2)$ gibi farklı iki noktadan geçen doğrunun eğimi ve denklemi, Ökl,t düzleminde olduğu gibi tanımlanır ve elde edilir.
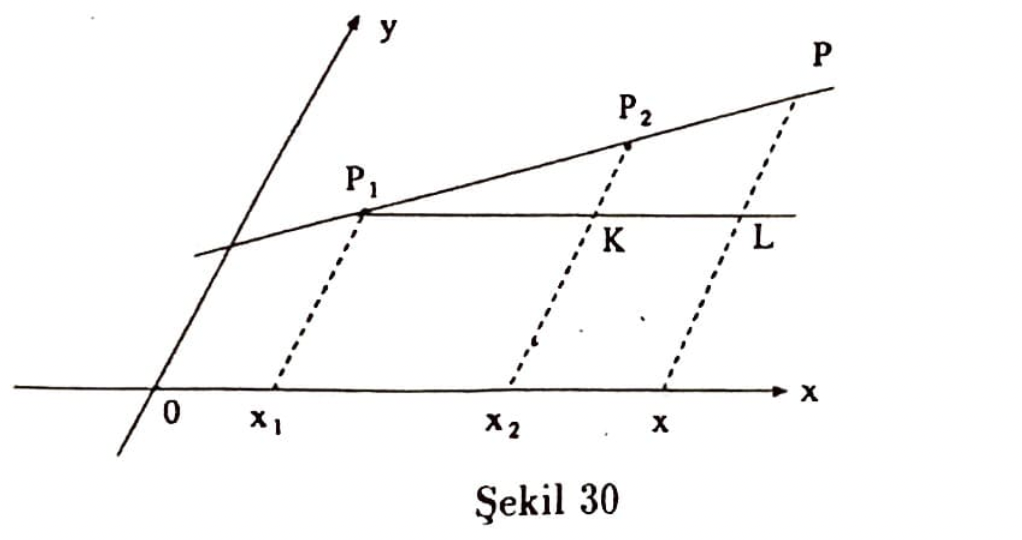
Eğimi şöyle tanımlarız:
$$m(P_1,P_2) = \frac{\text{ordinatlar farkı}}{\text{apsisler farkı}}$$
$$\Rightarrow m = \frac{y_1-y_2}{x_1-x_2}$$
Buna göre $P_1,P_2$ nin denklemi
$$ y-y_1= m(y-y_1) \qquad (8) $$
olur.
Bu da doğruların genel denklemi olarak
$$ax + by + c=0 \qquad (9)$$
eşitliğini verir.
$P_1(x_1,x_2),P_2(x_2,y_2)$ den geçen doğrunun denkleminin determinant biçimi şudur:
$$ \begin{vmatrix} x&y&1 \\ x_1&y_1&1 \\ x_2&y_2&1 \end{vmatrix} = 0 \qquad (10)$$
Gerçekten, $x=x_i , y=y_i (i=1,2)$ aldığında eşitlik sağlanır ve determinantın, birinci satıra göre açıldığında, (3) biçiminde olduğu görülür.
Sonuç. $d$ ve $d^{\prime}$, eğimleri $m,m^{\prime}$ olan farklı iki doğru ise $d // d^{\prime} \Leftrightarrow m=m^{\prime}$ geçerlidir.
İlgin düzlemde diklik kavramı yer almadığından $mm^{\prime}=-1$ eşitliği diklik diye bir şey ifade etmez.
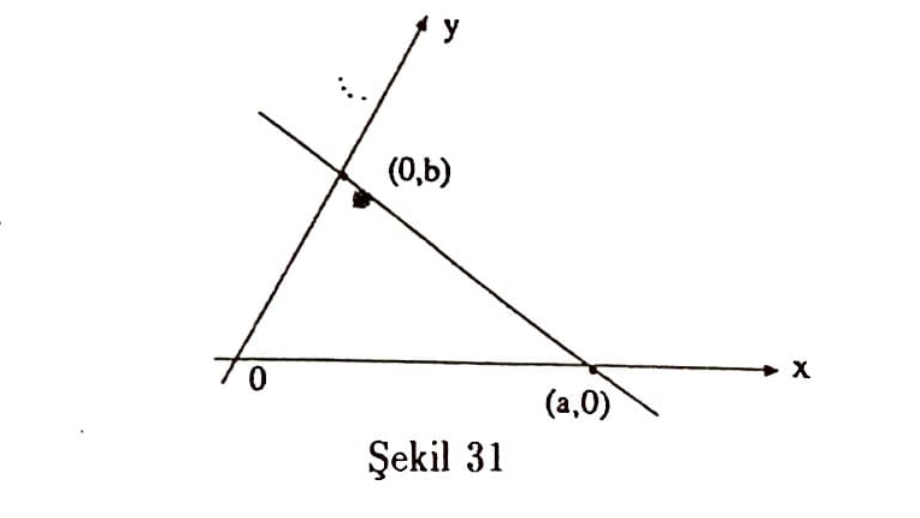
(4)’te $P_1(a,0),P_2(0,b)$ alındığında $P_1P_2$ nin denklemi olarak
$$ \frac{x}{a} + \frac{y}{b} = 1 \qquad (11)$$
elde edilir.
Üçgenlerin Alanları
İki hale ayıracağız:
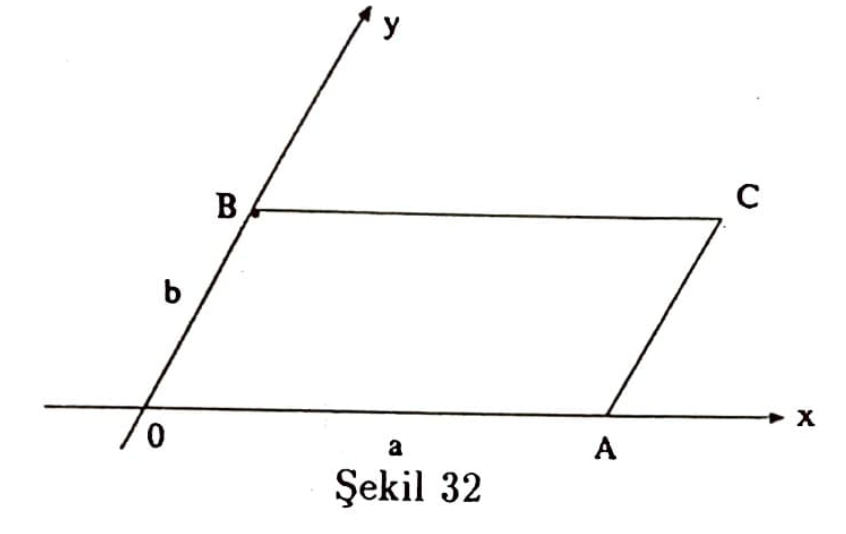
a) Köşelerinin koordinatları verilen üçgenin alanı. İlgin koordinat sisteminde $O(0,0) A(a,0) C(a,b) B(0,b)$ paralelkenarının alanını (Şekil 32)
$$ \mid OACB \mid = ab \qquad (12)$$
olarak tanımlıyoruz. Bu, Öklit koordinat sisteminde dikdörtgenin alanını verir.
Bir $P_1(x_1,y_1)P_2(x_2,y_2),P_3(x_3,y_3)$ üçgeninin alanını elde etmek üzere aşağıdaki şekillerde özel korunumlu koyu çizilmiş üçgenlerin alanları uanlarına yazılmıştır:
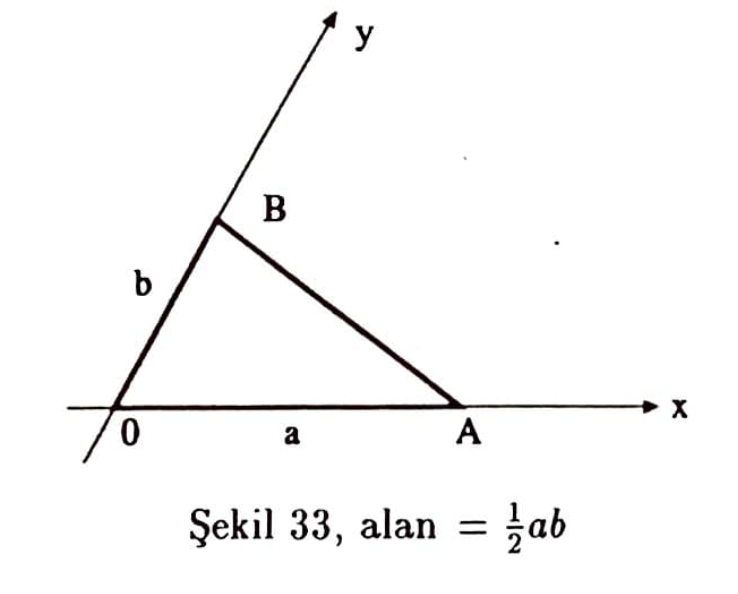
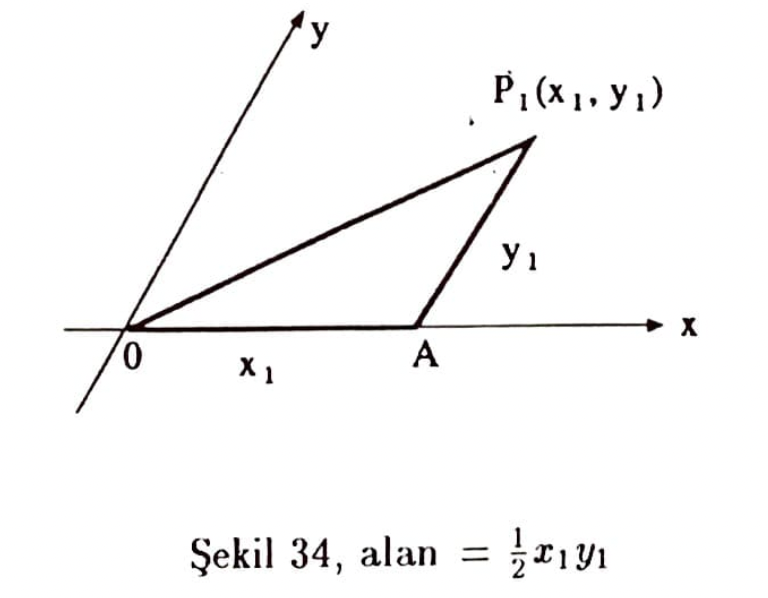
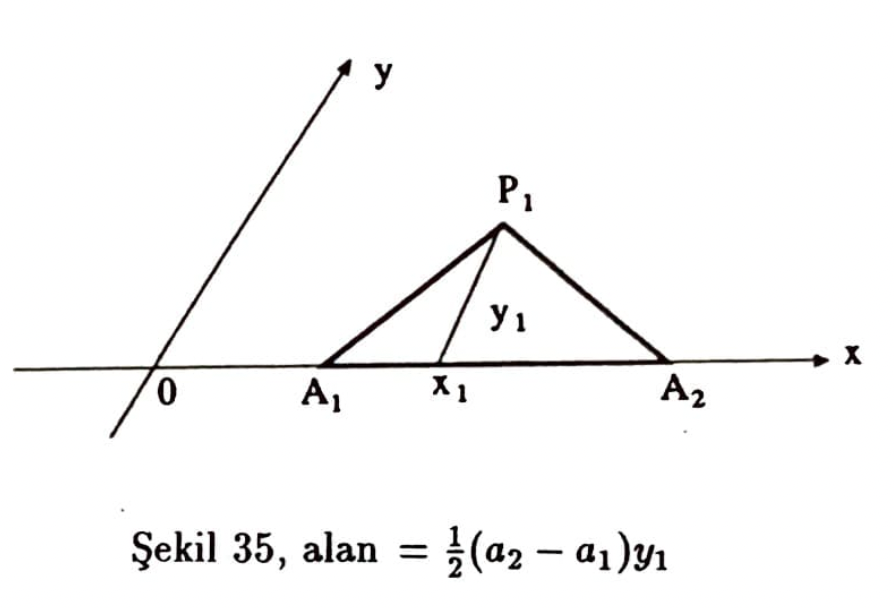
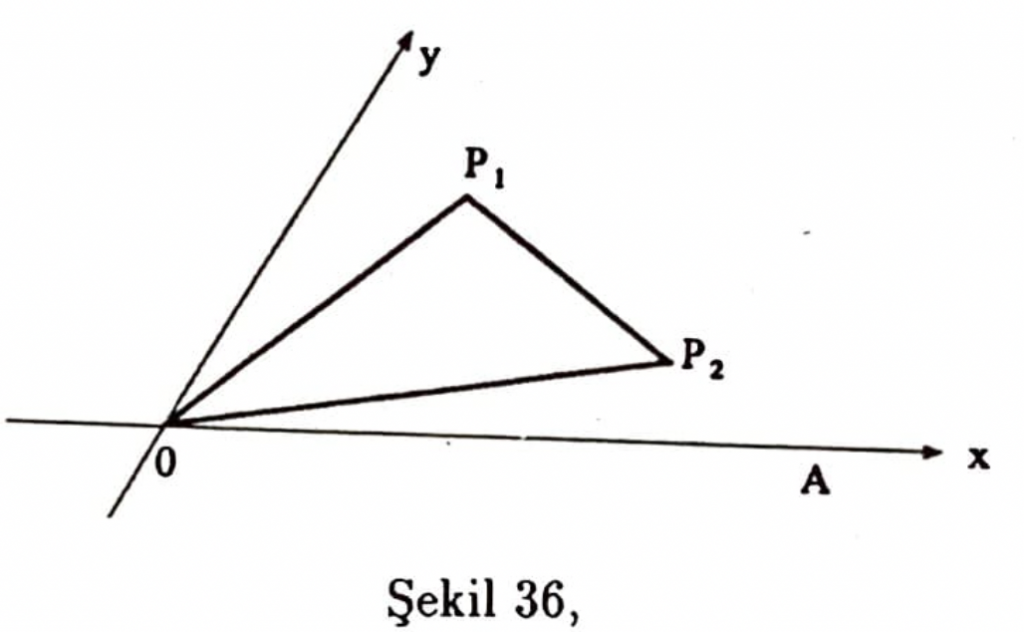
alan $\mid P_1OA\mid – \mid P_2OA \mid = \frac{1}{2}(x_1y_2-x_2y_1)$
Genel halde(Şekil 37)
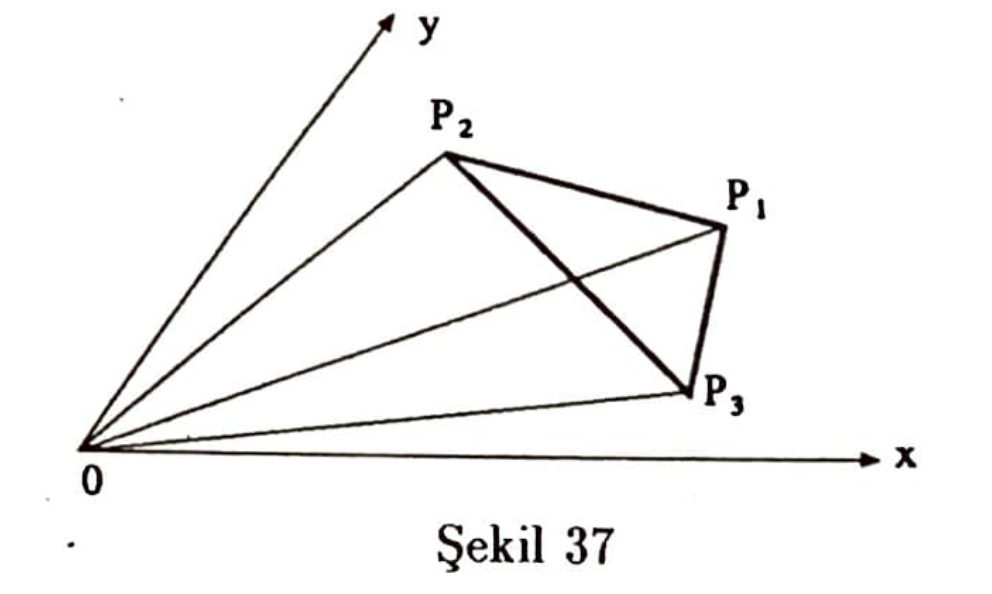
$$ \mid P_1P_2P_3 \mid= \mid P_1P_2O \mid + \mid P_1OP_3 \mid – \mid P_2OP_3 \mid$$
$$= (x_1y_2-x_2y_1) + \frac{1}{2} (x_1y_3-x_3y_1)$$
$$ -\frac{1}{2} (x_2y_3-x_3y_1)$$
olup
$$ \mid P_1P_2P_3 \mid = \frac{1}{2} \begin{vmatrix} x_1&y_1&1 \\ x_2&y_2&1 \\ x_3&y_3&1 \end{vmatrix} \qquad (13)$$
elde edilir.
Sonuç. Determinant sıfır olduğunda $P_1,P_2,P_3$ noktaları doğrudaştır.
b) Kenarlarına denklemleri verilen üçgenin alanı. Derginizde, ikişer ikişer kesişen ve denklemleri
$$a_{11}x+a_{12}y+a_{13}=0$$
$$a_{21}x+a_{22}y+a_{23}=0$$
$$a_{31}x+a_{32}y+a_{33}=0$$
olan $d_1,d_2,d_3$ gibi üç doğrunun oluşturudğu $d_1,d_2,d_3$ tam üçgeninin $\mid d_1d_2d_3\mid$ alanının hesaplanması sorulmuş (Mtematik Dünyası, Cilt 2, Sayı 3, s.23 Y38) ve cevabın
$$ \mid d_1,d_2,d_3 \mid = \frac{\begin{vmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{vmatrix}^2}{A_{13}A_{23}A_{33}} \qquad (14)$$
olduğu ispatlanmıştır(Matematik Dünyası,Cilt 2, Sayı 5, s.31). Burada $A_{13},A_{23},A_{33},$ kofaktörleridir.
Sonuç. (7)’de verilen determinant sıfır olduğundan $d_1,d_2,d_3$ doğruları noktadaştır.
Şimdi bu iki sonucun bazı uygulamalarını verelim.
Teorem. (Newton Doğrusu). Bir tam dörtgende köşegenlerin orta noktaları doğrudaştır.
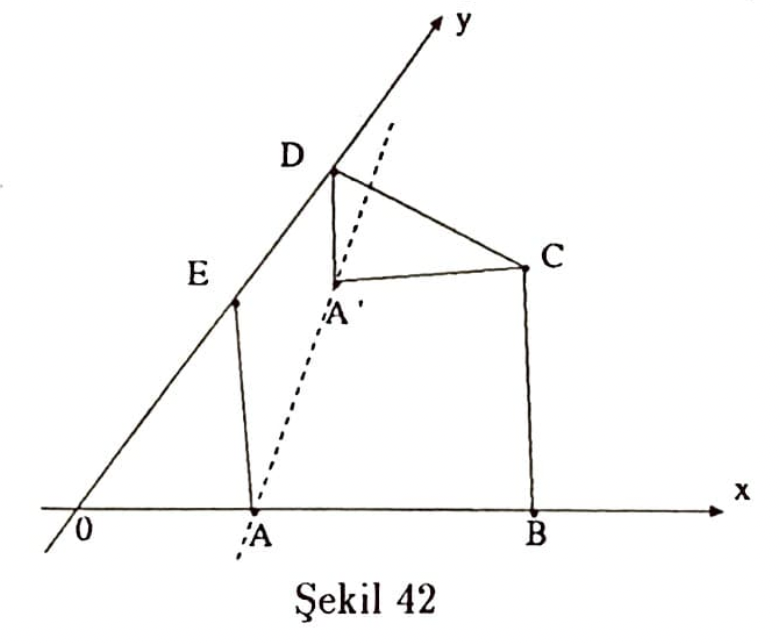
Bir $ABC$ üçgeni ile bir $DEF$ keseninden oluşan bir dörtgeni koordinat sistemine Şekil 38’deki gibi yerleştirerek
$$ B(0,0), C(2c,0), D(2d,0), A(0,2a), F(0,2f)$$
koyalım.
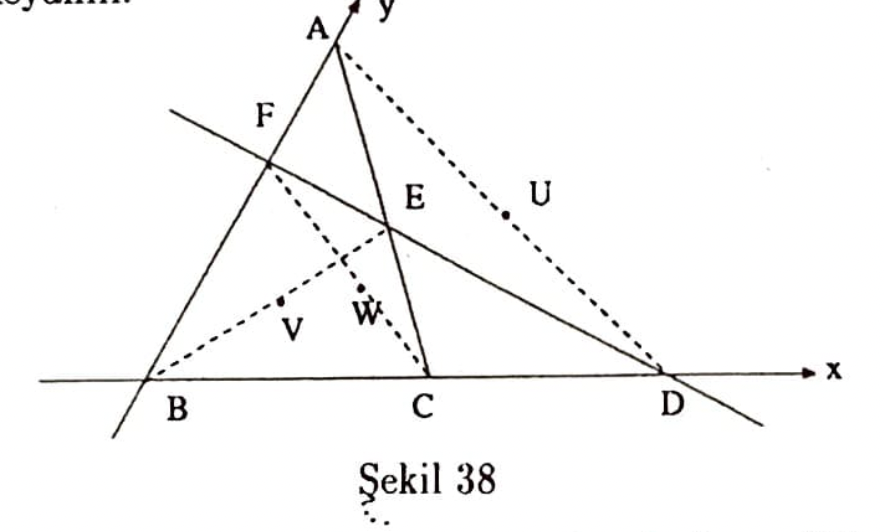
$E$ nin koordinatlarını bulmak üzere (5)’i kullanarak $AC$, $DF$ nin
$$\frac{x}{2c} + \frac{y}{2a} = 1 \Rightarrow ax+cy=2ac$$
$$\frac{x}{2d} + \frac{y}{2f} = 1 \Rightarrow fx+dy=2df$$
bulup denklemlerini ortak çözelim.
$$E \left( 2cd \frac{a-f}{ad-cf}, 2af \frac{d-c}{ad-cf} \right)$$
bulunur ve (6)’dan hesaplar sonucu
$$ \begin{vmatrix} d&a&1 \\ c&f&1 \\ cd\frac{a-f}{ac-cf}&af\frac{d-c}{ad-cf}&1 \end{vmatrix} = 0$$
elde edilir.
Meraklı okurlara şu iki teoremin analitik ispatlarını vermelerini öneriyoruz.
Teorem. (Pappus). $p,p^{\prime}$ gibi iki doğru üzerinde $A,B,C$ ve $A^{\prime},B^{\prime},C^{\prime}$ noktaları bu sıralamalarla alındığında $BC^{\prime} \cap B^{\prime}C,CA^{\prime} \cap C^{\prime}A, AB^{\prime} \cap A^{\prime}B$ noktaları doğrudaştır (Şekil 39).
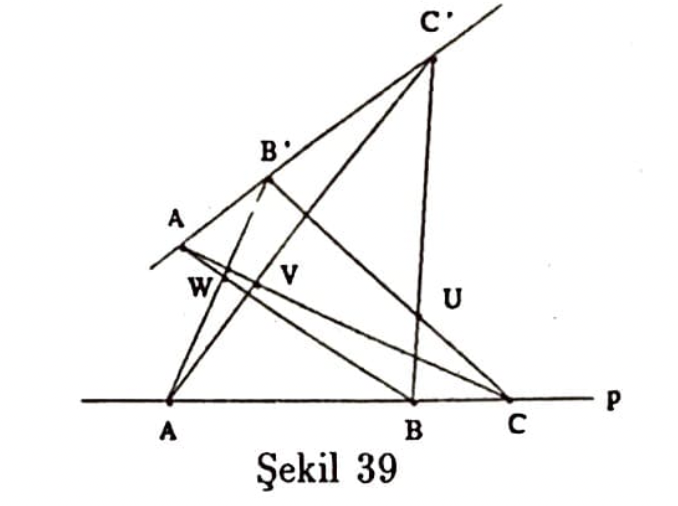
Teorem. $DEF$ doğrusu bir $ABC$ üçgeninin bir keseni(Şekil 40) ve $ AEA^{\prime}F,BFB^{\prime}D,CDC^{\prime}E$ birer paralelkenar ise $A^{\prime},B^{\prime},C^{\prime}$ doğrudaştır.
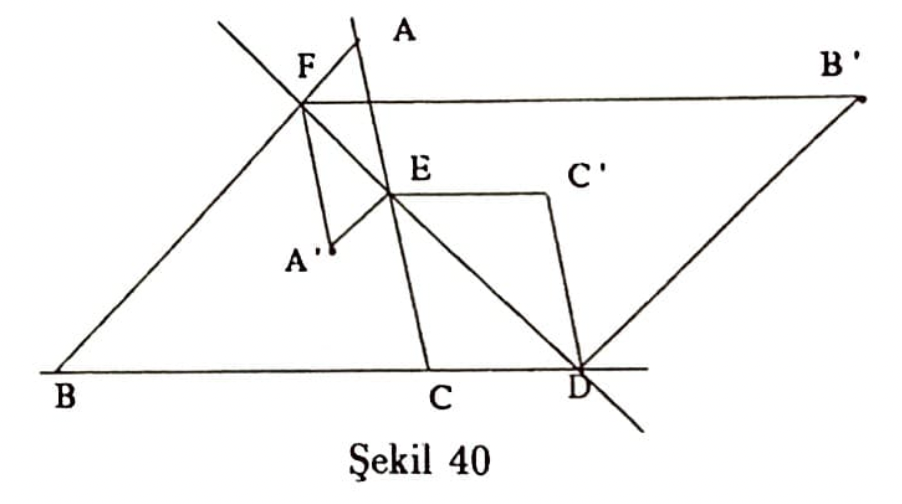
Şimdi doğruların noktadaşlığına ilişkin iki örnek verelim.
Teorem. Bir üçgende kenarortaylar noktadaştır.
Üçgen $ABC$ olsun ve $BC$ doğrusu $x$ ekseni, $BA$ doğrusu ise $y$ ekseni seçilsin.
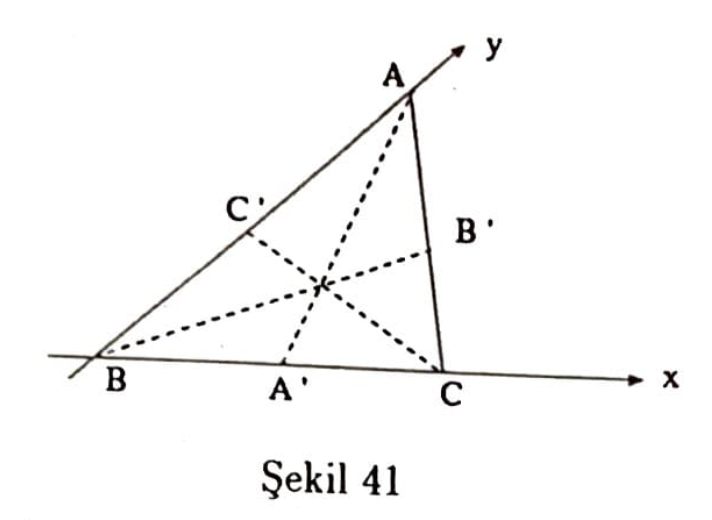
$A(0,2a), B(c,a), C(2c,0)$ koyup $A^{\prime}(c,0), B^{\prime}(c,a), C^{\prime}(0,a)$ elde edilir.
Kenarortayların denklemleri olarak şunları buluruz:
$$AA^{\prime} : \frac{x}{c} + \frac{y}{2a} = 1 \Rightarrow 2ax+ccy-2ac=0$$
$$BB^{\prime} : \frac{y}{x} = \frac{a}{c} \Rightarrow ax-cy=0$$
$$CC^{\prime} : \frac{x}{2c} + \frac{y}{d} = 1 \Rightarrow ax+2cy-2ac=0$$
Bunlara da (7) uygulanırsa deteminantın sıfır olduğu görülür:
$$\begin{vmatrix} 2a&c&-2ac \\ a&-c&0 \\ a&2c&-2ac \end{vmatrix} = 0 $$
Teorem. Bir $ABCDE$ beşgeninde $A$ köşesinden geçen $AB,AC$ doğrularına, $A$ nın karşı $\left[CD\right]$ kenarının $C,D$ uçlarından çizilen paralel doğrular bir $A^{\prime}$ noktasında kesişsinler $(A^{\prime}C//AB,A^{\prime}D//AE)$. Benzer çizimlerle $B^{\prime},C^{\prime},D^{\prime},E^{\prime}$ noktaları bulunursa $AA^{\prime},BB^{\prime},CC^{\prime},DD^{\prime},EE^{\prime}$ doğruları noktadaştır.
Konikler.
Konikler ikinci dereceden eğriler olup genel denklemleri
$$Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0 \; \qquad (15)$$
biçimindedir.
İlk üç katsayıdan en az biri sıfırdan farklıdır ve kkoniğin türü dış koinvariant denilen
$$\Delta = B^2-AC \qquad (16)$$
sayısının işaretiyle belirlidir. $\Delta$’nın negatif sıfır ya da pozitif olması halinde konik elips, parabol ya da hiperboldür.
Konumuzu bir problemle kapatıyoruz.
Problem. Bir üçgenin çevrel elipslerinin merkezlerinin geometrik yerini bulunuz.
Bu geometrik yeri tahmin etmek oldukça zordur. Çözüme ancak analitik olarak ulaşabiliriz.
Üçgenin köşeleri $A(0,1),B(0,0),C(1,0)$ olarak alındığında (Şekil 43), elips $(0,0),(1,0)$
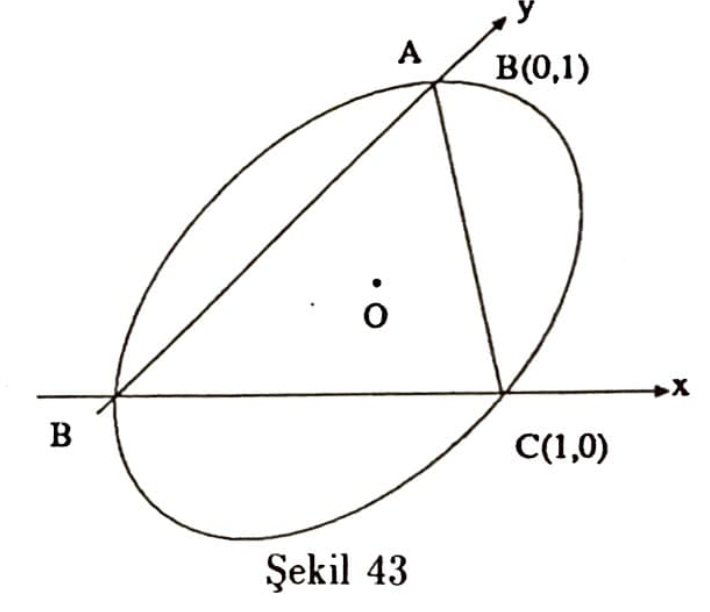
$(0,1)$ noktalarından geçtiğinden
$$F=0, A+2D=0, C+2E=0$$
elde edilir ve (8) denklemi
$$f(x,y) \equiv Ax^2+2Bxy+Cy^2-Ax-Cy=0 \qquad (8^{\prime})$$
denklemine dönüşür.
Elipsin $O(x_0,y_0)$ merkezi
$$f_x = 2Ax+2By-A=0$$
$$f_y = 2Bx+2Cy-C=0$$
denklem sistemini sağlar. Sistem çözüldüğünde
$$2\Delta x_0 = BC-AC$$
$$2\Delta y_0 = BA-AC$$
elde edilir. $AC$ yerine (9)’dan $B^2-\Delta$ yazıldığında
$$(2x_0-1)\Delta = BC-B^2$$
$$(2Y_0-1)\Delta = BA-B^2$$
bulunur.
Bunlardan $B^2$ yi sola geçirerek elde edilen eşitlikler taraf tarafa çarpıldıpında ve $AC \equiv B^2-\Delta$ kullanıldığında kısaltmalardan sonra
$$(2x_0-1)(2y_0-1)\Delta+(2x_0+2y_0-1)B^2=0$$
$$\Rightarrow (2x_0-1)(2y_0-1)(2x_0+2y_0-1)+(2x_0+2y_0-1)^2({B^2}/{\Delta})=0$$
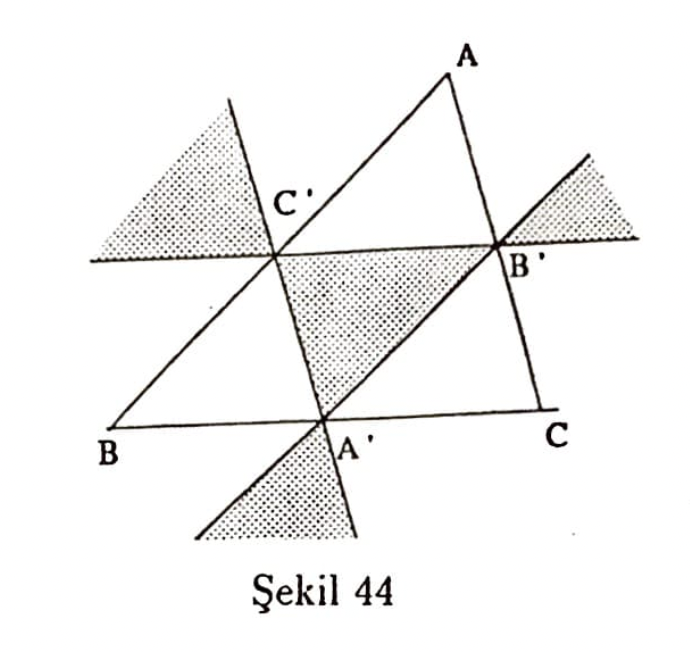
$$\Rightarrow (2x_0-1)(2y_0-1)(2x_0+2y_0-1)-(2x_0+2y_0-1)^2({B^2}/{\Delta})\geq 0$$
elde edilir. Bu eşitsizlik ise $ABC$ nin $A^{\prime}B^{\prime}C^{\prime}$ orta tam üçgeni ile ilgili taralı bölgeyi verir.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Emre Kahvecioğlu‘na ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

