Yazar: Burçak Boz Yaman, Melike Yiğit Koyunkaya (burcak@mu.edu.tr, melike.koyunkaya@deu.edu.tr)
Yıl: 2022-2
Sayı: 112
Nasıl matematik öğreniriz? Başka bir deyişle matematiksel bilgiyi nasıl inşa ederiz? Son yüzyıldır öğrenmeyi tanımlamak ve geliştirmek amaçlı davranışçılık, bilişselcilik ve yapılandırmacılık gibi birçok yaklaşım geliştirilmiştir. Her bir yaklaşım öğrenmeye farklı bakış açısıyla bakarken, ulusal ve uluslararası eğitim sistemlerine yön veren yapılandırmacılık teorisi matematik öğrenmeyi tanımlama ve geliştirme anlamında en yaygın kullanılan teori olmuştur. Ernest [1] yapılandırmacılığın matematik eğitimi araştırmalarının merkezinde bulunan bir felsefe olduğunu söyler. Peki yapılandırmacılığa göre birey, matematiksel bilgiyi nasıl yapılandırır? Bu soruyu cevaplamak adına önce teorinin kurucularından biri ve matematik öğrenme teorileri denilince neredeyse ilk akla gelen kişi olan Jean Piaget’nin öğrenmeye dair çalışmalarını anlamakla başlayalım.
Piaget [2] geliştirdiği teoriyi insan bilgisine dair gelişim teorisi olarak tanımlarken, buna genetik epistemoloji adını vermiştir. Bilginin birey tarafından pasif olarak alınmadığını, aksine bilgiyi bireyin kendisinin yapılandırdığını savunduğu teorisinde, bilgiyi bir nesne olmaktan çok bir süreç olarak ele almaktadır. Piaget’ye göre bilgi, bireylerin olgu veya nesnelerle ilişkisi sonucu oluşur. Bu durumsa bilginin birey tarafından yapılandırılmasına imkân verir. Öğrenme sürecinde oluşan şema (veya zihinsel düzenek) ise yeni bilginin yerleştirileceği bir çerçevedir. Şemalar bilginin yapılandırıldığına dair bir kanıt olmasının yanı sıra tekrarlanabilir, yeni bilginin inşa sürecinde gerekli durumlara uygulanabilir ve genellenebilirdir. Ayrıca şemalar, canlının uyum sağlamasını ve bilgiyi organize etmesini sağlar. Piaget’ye göre uyumun iki bileşeni vardır: özümseme ve düzenleme. Özümseme, bireyin sahip olduğu şemalar ile çevresindeki yeni durumlara uyumu sağlayan bir süreçtir. Özümseme süreci, bireyin yeni durumu içselleştirmesi sürecidir. Zaman zaman yeni durum bireyde var olan şemalara tam olarak uyum sağlayamayabilir. Mevcut bilgi ve şemalar yeni gelen bilgiye dair yeterliyse sadece özümseme yapılması yeterlidir, ancak yeni bilgi hazırdaki şemaya uyumlu değil ve bir dengesizlik yaşanmaktaysa şema düzenlenir ve denge durumuna geçilerek şema revize edilir. Özümseme ve düzenleme yaşam boyu devam eden süreçlerdir. Öğrenme için dengesizlik hali yeni şemaların oluşturulması ve düzenleme yapılmasıyla denge haline gelir. Dengenin kurulması sürecinde öğrenme gerçekleşir ve bu durum her bir kavram için yeniden yaşanır. Böylece yeni şemalar ve uyum süreci devam eder.
Piaget öğrenmenin çeşitli seviyelerde gerçekleşeceğini vurgulamış ve bu durumu soyutlama kavramını ele alarak açıklamıştır. Piaget tüm yeni bilgileri bir soyutlama olarak düşünmektedir. Dolayısıyla bilişsel gelişimin bir düzeyinden diğerine geçmek için soyutlama önemli bir rol oynamaktadır. Soyutlamanın 2 farklı şekli olan deneysel ve yansıtıcı soyutlamayı Piaget şöyle açıklar: Deneysel soyutlamada fiziksel dünyanın gözlemlenebilen özellikleri temel alınırken, yansıtıcı soyutlamada bireyin kendi eylemleri ve bu eylemlerin koordineli kullanımına dair özellikler söz konusudur. Deneysel soyutlamada yeni bilgi, bireyin çevresindeki nesneler ve gözlemlerinden oluşur. Piaget ve Garcia’ya [3] göre bu şekilde elde edilen bilgiye dışsal veya dış kaynaklı bilgi denir. Yansıtıcı soyutlamanın bilgi kaynağıysa mantıksal matematiksel bilgi olmak üzere bu soyutlamanın temel bileşenleri özümseme ve düzenlemedir. Yansıtıcı soyutlama, bilişsel gelişimin en erken aşamalarında dahi mevcuttur ve bu süreç daha ileri matematiksel kavramların öğrenim süreci boyunca da devam eder [4]. Var olan bilgiden daha ileri düzey bir bilginin yapılandırılması için yansıtıcı soyutlama gereklidir. Öğrenmenin gerçekleşme sürecinde, yeni bilgi bireyin hazırdaki var olan şemasıyla uyumlu değilse bahsedilen dengesizlik durumu yaşanır, yani şemanın revize edilme süreci başlar. Diğer bir deyişle, bireylerin yeni bilgiyi özümseyerek mevcut bilgiye uyarlaması ve geliştirmesi gerekir. Sonunda da mevcut bilgilerini ortadan kaldırırlar ve yeni bilgiyi tamamen içeren daha karmaşık bir zihinsel düzeneği benimserler. Deneysel olanın aksine, yansıtıcı soyutlama yoluyla elde edilen bilgiye içsel veya iç kaynaklı bilgi denir.
Piaget’yi ve onun çalışmalarını takip ederek bir süredir yaptığımız iki farklı araştırmada öğrencilerin fonksiyon dönüşümleri konusundaki öğrenme süreçlerini incelemekteyiz. Bu çalışmalarda fonksiyon dönüşümlerini $y=f(x)$ temel fonksiyonunun eksenler üzerinde ötelenmesi ($a, b$ ve $c$ birer reel sayı olmak üzere $f(x + a)$ veya $f(x) + b$) veya grafiğin eksenlere yaklaşması ya da uzaklaşması (bir katsayı ile çarpılması yani $c\cdot f(x)$) şeklinde ele aldık. Bu çerçevede bir lise öğrencisi ve üniversitede matematik öğretmenliği programlarında öğrenim gören öğrencilerle bireysel olarak veya az sayıdaki kişilerden oluşan küçük gruplarda yaptığımız çalışmalarda dönüşüme uğrayan fonksiyonların grafiklerini verip, öğrencilerden cebirsel gösterimlerini bulmalarını istedik. Aynı şekilde dönüşüme uğrayan fonksiyonun cebirsel denklemini verip temel fonksiyonu ve ona uygulanan dönüşümü izleyerek yeni fonksiyonun grafiklerini çizmelerini bekledik. Bu araştırmaların birinde yer alan bir üniversite öğrencisinin fonksiyon dönüşümlerini zihninde yapılandırarak öğrenme sürecini Piaget’nin yapılandırmacılık teorisi bağlamında tartışmak isteriz. Sizler de öğrencilerinizin benzer sorulara dair düşüncelerini tahmin etmeye çalışıp, burada verilen ve bizim karşılaştığımız örnek durumların üzerinde yorum yaparak fonksiyon dönüşümlerine yönelik akıl yürütmeleri inceleyebilirsiniz.
Öncelikle Şekil 1’deki gibi bir fonksiyon grafiğini öğrencilerinize verip, bu grafiğe karşılık gelen ikinci derece fonksiyonun denklemini bulmalarını istediğinizde, sizce öğrencileriniz nasıl bir çözüm yolu izleyeceklerdir?
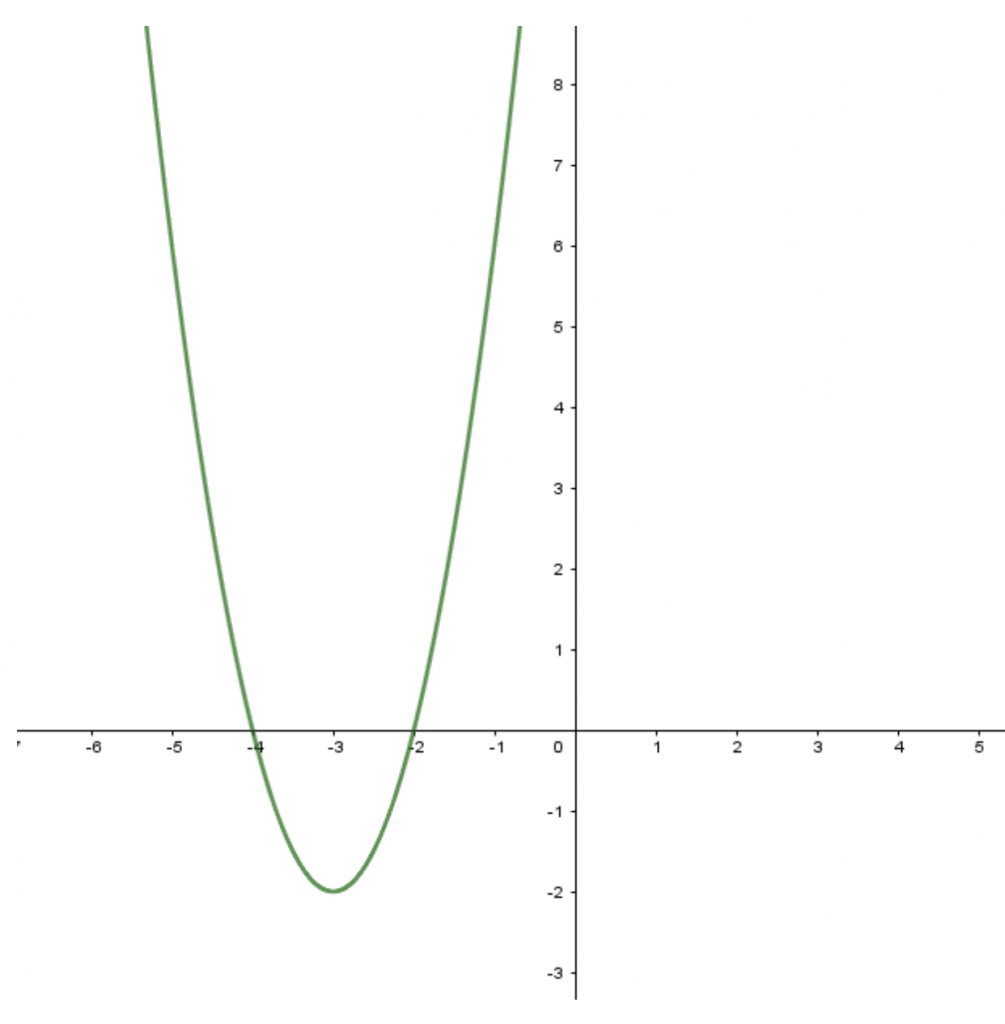
Olası cevaplar arasında, “Tepe noktasını ve parabolün eksenleri kestiği noktaları göz önünde bulundurup, bu değerleri genel parabol denkleminde yerine yazarak istenen denklemi bulacaklar” dediğinizi duyar gibiyiz. Bir öğretmen bu soruyu sorup bahsi geçen cevabı aldığında, aşağıda araştırmalarımız sonucu etkili olabileceğini düşündüğümüz dizisel uygulamalarla öğrencilerin fonksiyon dönüşümlerini öğrenme sürecini destekleyebilir. Bir öğretmen düşünelim, bu soruyu sorduğunda, karşısındaki öğrenci $T = \frac{-b}{2a}$ tepe noktası ve $y = ax^2 + bx + c$ genel parabol denklemlerini kullanarak istenen grafiğin cebirsel denklemini elde etsin [5]. Diğer bir deyişle, öğrenci grafikten fonksiyonun tepe noktasını $(-3,-2)$ ve fonksiyonun eksenleri kestiği noktalar olan $(-4,0)$ ve $(-2,0)$ noktalarını belirledikten sonra cebirsel işlemler yapsın. Öğrencinin bu soruya yönelik cevabı yanlış bir çözüm olmamakla birlikte, izlediği yol denklem bulmak için formül kullanma yaklaşımının ötesine gidemez. Her ne kadar formül kullanmanın yanlış olduğunu söylemiyorsak da, öğretmen bu örnekte öğrencinin daha farklı kavramsal bir yaklaşım sergilemesini ve fonksiyon dönüşümü kavramını içselleştirebildiğini görmek istemektedir. Bu süreçte öğretmen, öğrencinin öncelikle ikinci dereceden fonksiyon ailesinin temel fonksiyonu olarak $y = x^2$ parabol fonksiyonu olduğunu hatırlamasını sağlamalıdır. Daha sonra da $x$’in karesini içeren benzer formlara ($a, b$ ve $c$ tamsayılarına bağlı olarak ifade edilen $f(x+a), f(x) + b$ ve $c\cdot f(x)$ formundaki fonksiyonlar) sahip fonksiyonların cebirsel denklemini elde etme yolu olarak, bu temel fonksiyonunun grafiğinin eksenler üzerinde ötelenmesi ve kollarının daralması veya genişlemesi durumları üzerine incelemeler yaptırmalıdır. Bu incelemelerde önemli noktalardan birisi dizisel öğrenme yaklaşımıdır yani öğrencinin ilk önce eksenler üzerinde öteleme yapıp daha sonra karmaşık (örneğin bahsi geçen tüm $a, b$ ve $c$ katsayılarını içeren) denklemlere geçiş yaparak parabolün kollarının açılıp kapanması durumunu ele alması ve böylece fonksiyon dönüşümlerine dair bilgiyi yapılandırabilmesidir. Diğer bir önemli noktaysa öğretmenin rolü olup, öğrencinin fonksiyon dönüşümlerinin aslında fonksiyon grafiklerinin ötelenmesiyle oluşabileceğine dair bilgisini yapılandırmasını desteklemesidir. Bu yeni bilginin yapılandırılmasında, öğrenci fonksiyon tanımı, öteleme dönüşümü, parabol fonksiyonun grafiği gibi ön bilgilerini temel alacak ve grafiği verilen fonksiyonun denkleminin, $f(x) = x^2$ fonksiyonunun bir dönüşümü olduğu sonucuna ulaşacaktır.
Öğretmen bir fonksiyonun $x$ ekseni üzerinde ötelenmesi kavramını inceletirken, öğrencinin bir dinamik matematik yazılımı (GeoGebra gibi) kullanarak grafikte meydana gelen değişimleri gözlemlemesini isteyebilir. Bu süreçte öğrenci yazılımın ekranındaki koordinat düzleminde grafiğin konumunu değiştirirken, öğretmenin “$1$ birim sağa öteledin, grafiğin denkleminde parantez içinde $x$’in yanında $(-1)$ gelerek $f(x) = (x-1)^2$ oldu, $2$ birim sağa öteledin $x$’in yanına $(-2)$ gelerek $f(x) = (x-2)^2$ oldu. Benzer şekilde $1$ birim sola ötelediğinde de $x$’in yanında $(+1)$ oldu ve fonksiyon $f(x) = (x+1)^2$ şeklinde görüldü” gibi gözleme dayalı olarak açıklamalar yapması, öğrencinin meydana gelen değişikliği sadece gözlemlemesine destek olabilirken kavramsal olarak bu değişikliği anlamlandırmasında etkili olmayacaktır. Çünkü bu uygulama öğrencinin temel fonksiyon ile dönüşüme uğramış yeni fonksiyon arasındaki ilişkiyi içselleştirebilmesini kolaylaştırmamaktadır.
Öğrencinin var olan bilgisini revize edip daha ileri düzeyde yapılandırmasını sağlamak için daha farklı bir yol önerelim ve bunun nasıl olabileceğini yaptığımız araştırmaların sonuçlarına dayanarak adım adım sizinle paylaşalım: Uygulamadaki temel amaç öğrencinin verilen bir fonksiyonun cebirsel denkleminin $f(x) = 2(x+3)^2 -2$ grafiğinin çizimi esnasında değişkenlere değer verme veya formül kullanma şeklinde değil, eksenler üzerinde öteleme ve parabolün kollarının durumunu göz önünde bulundurarak çıkarım yapma yoluyla çizebilmesidir. Öğrencinin çıkarımları yapma esnasında bir bilginin yapılandırma sürecini anlatalım.
İlk olarak öğretmen, öğrenci grafiğe bakarken, “Verilen grafiğin ($f(x) = 2(x+3)^2 – 2$) elde edilmesi için $f(x) = x^2$ temel fonksiyonu nasıl bir değişime uğramalıdır?” sorusunu veya buna benzer bir soruyu sorduğunda, öğrenci bu yönergeyle birlikte fonksiyonun grafiğinin konumunda ve formunda değişiklikler olduğuna dair çıkarımlar yapabilir. Fakat bu farkındalık ve çıkarım yapabilme eylemleri kavrama dair yeni şemanın oluşması ya da var olan şemanın genişletilmesi için yeterli değildir. Yukarıda da bahsedildiği gibi, hedeflenen şekilde bilginin yapılandırılması için öğretmen önce eksenler üzerindeki ötelemeye, daha sonra da parabolün kollarının açılıp/kapanma durumlarına vurgu yapıp, süreci bir rehber gibi yöneterek öğrencinin bilgiyi kendisinin yapılandırmasını sağlamalıdır. Öğretmen, öteleme kavramına vurgu yaparak, öğrencinin koordinat düzleminde ötelemeye dair var olan ön bilgilerini kullanıp, yeni bilginin inşasını içselleştirme sürecini desteklemelidir. Piaget’nin öğrenme teorisindeki var olan şemaların yeni bilginin inşasında kullanılması düşüncesinden yola çıkarak, öğrencinin bir nesnenin koordinat düzleminde ötelenmesine dair sahip oldukları şemalarının kullanılması fonksiyon dönüşümleri konusundaki yeni şemanın oluşmasını destekleyebilir. Öğretmen, bir $A(x,y)$ noktasının koordinat düzleminde $x$ ekseninde $3$ birim sola ve $y$ ekseninde $2$ birim aşağıya ötelenmiş hali olan $A'(x-3, y-2)$ noktası olduğunu öğrenciyle tartışarak ve hatta bu tartışmayı bir dinamik matematik yazılımı (GeoGebra gibi) eşliğinde yaparak, öğrencinin bir $y=f(x)$ fonksiyonu grafiğinin de eksenler üzerinde ötelenebileceği durumunu anlamlandırmasını sağlayabilir. Bu süreçte öğretmen, öğrencinin Şekil 2’deki gibi $f(x) = x^2$ fonksiyonuna göre verilen fonksiyonun grafiğinin $y$ ekseninde $2$ birim aşağıya ve $x$ ekseninde de $3$ birim sola ötelenmiş haline benzediğine dair bir çıkarım yapmasını destekleyici yönergelerde bulunmalı ve öğrencinin yeni bilgiyi yapılandırmasını güçlendirecek şekilde sorular sormalıdır. Bu örneğin temel amacı da öğrencinin hedeflenen bilgiyi yapılandırması sürecinde öğretmenin hangi sorularla öğrenci düşüncesini ortaya çıkarıp, hedeflenen bilgiyi yapılandırması için nasıl rehber olabileceğini göstermektir. (Bu incelemeleri siz de GeoGebra ekranında yapmak ve kendi sorgulama sürecinizi oluşturmak için verilen bağlantıyı kullanarak $a, b$ ve $c$ sürgüleri yardımıyla temel fonksiyonun katsayılarını değiştirip eş zamanlı olarak ekranda öteleme ve daralma/genişleme hareketlerini gözlemleyebilirsiniz. Soldaki cebir penceresindeki her bir fonksiyonun sol tarafındaki daireleri işaretleyerek fonksiyon grafiklerini açıp/kapatıp süreci yönetebilirsiniz: https://www.geogebra.org/m/rmfh5vr
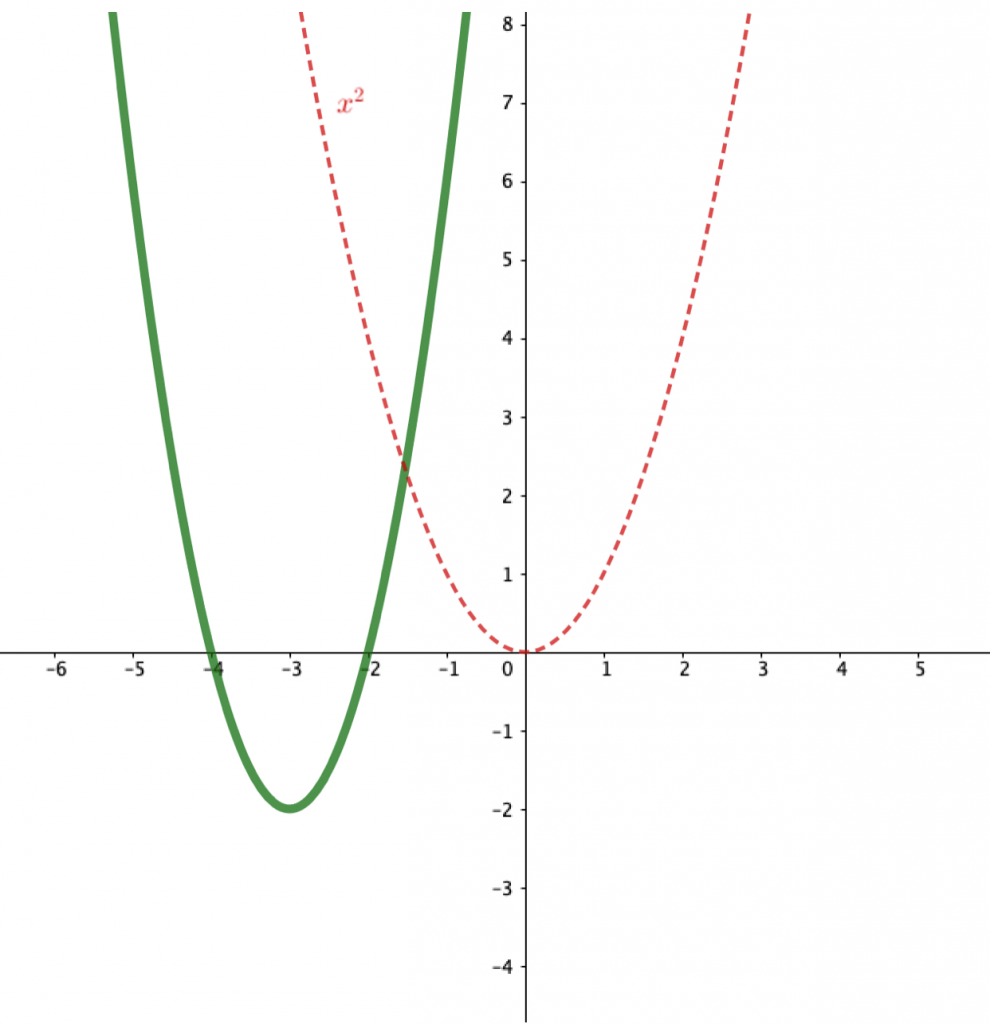
Sorulabilecek sorular şöyle olabilir:
- Temel fonksiyona ($f(x) = x^2$) göre verilen grafik $x$ ekseni boyunca nasıl bir hareket yapmış olabilir? Neden böyle düşünüyorsun, açıklar mısın?
Bu sorudaki temel amaç, öğrencinin dönüşüme uğramış olan fonksiyonun $x$ eksenindeki hareketini içselleştirmesi için temel fonksiyonun $x$ ekseninde sola haeketinin sonucunda oluşacak fonksiyon ifadesini yapılandırmasını sağlamaktır. Öğrenci bu soruya cevap olarak grafik sola doğru yer değiştirmiş şeklinde yanıt verebilir. Öğretmen, GeoGebra gibi dinamik bir matematik yazılımı kullanarak (Şekil 3), öğrencinin fonksiyonda meydana gelen hareketi adım adım görmesini sağlayabilir. Öğrencinin neden sola hareket eden bir fonksiyonun yeni formülünün ekranda gördükleri gibi $f(x) = (x+3)^2$ haline dönüştüğünü sorgulaması desteklenmelidir. Öğrenci fonksiyon hareket edip konumu değiştikçe, ekrandaki cebirsel denklemde eş zamanlı oluşacak değişikliği anlamlandırırsa, bilginin inşa süreci güçlendirilebilir. Bu noktada öğretmen adım adım;
- $f(x) = x^2$ fonksiyonu $2$ birim sola kaydırıldığında $y$ değerlerinin aynı kalmasını sağlayan fonksiyonun denklemi ne olabilir söyler misin?
- Peki $2$ birim sağa kaydırıldığında oluşan fonksiyonun denklemi ne olabilir söyler misin?
- Peki $3$ birim sola, $4$ birim sola; aynı şekilde $3$ birim sağa ve $4$ birim sağa…
- Peki tüm yaptığımız uygulamaları göz önünde bulundurarak, $f(x) = x^2$ fonksiyonunun $x$ ekseni üzerinde sağa ve sola konum değiştirirken, aynı zamanda $y$ değerlerinin sabit kalmasıyla ilgili bir genelleme yapabilir misiniz?
şeklinde sorular sorarak öğrencilerin bu bilgiyi yapılandırmalarını destekleyebilir. Öğrenci genellemeye varamadığı durumlarda, öğretmen öğrencinin var olan ön bilgisini de göz önünde bulundurup “bir noktada ötelemeyi düşünelim, nokta koordinat düzleminde $x$ ekseni boyunca konum değiştirdiğinde, yeni konumunda $x$ koordinatı değişirken $y$ koordinatı değişmemektedir. Bu durumu herhangi bir $x$ ve $y$ koordinatı için genellemek istersen ilk nokta ile ikinci noktanın $x$ ve $y$ koordinatlarını nasıl elde ettiğini yeniden açıklayabilirsin” gibi ön bilgileriyle ilişki kuracak şekilde ipuçları verebilir.
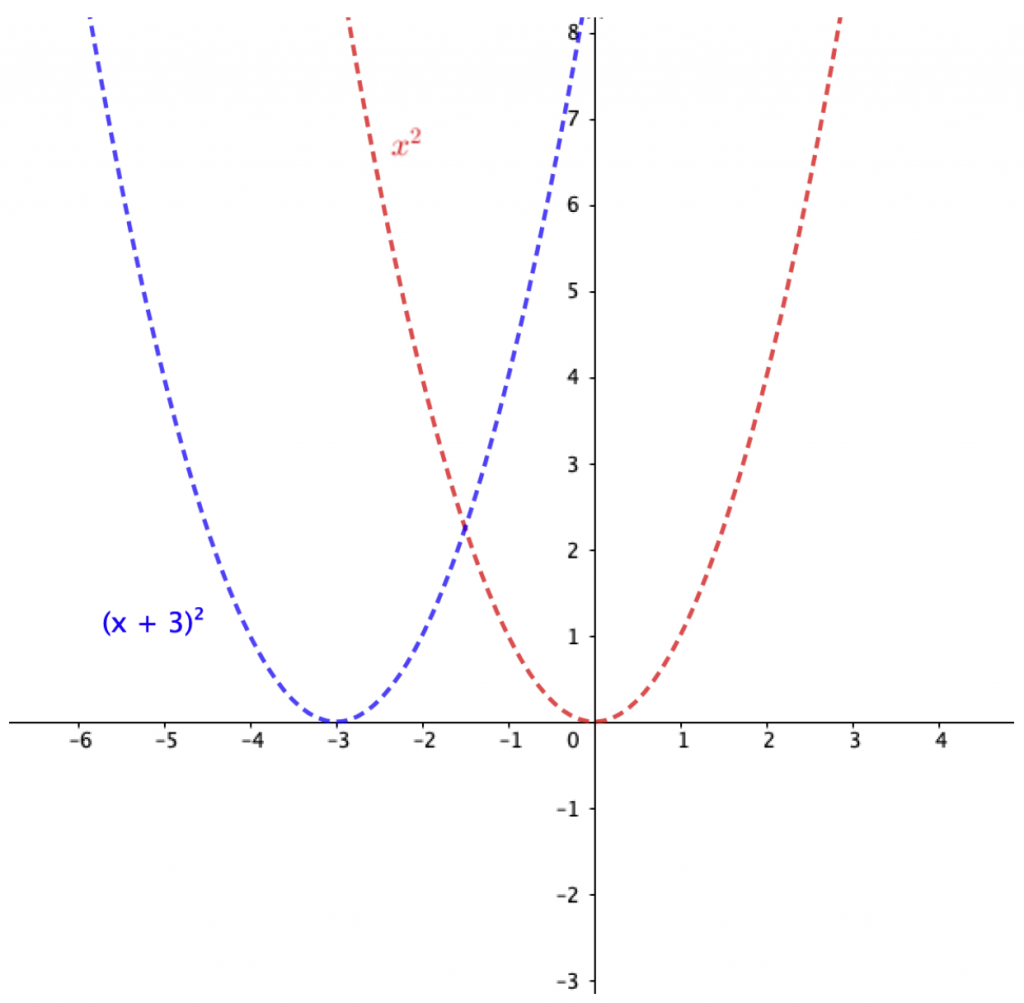
Etkinliğin uygulama sürecine dair önemli bir noktanın altını çizmek gerekirse, öğrencinin meydana gelen harekete dair sorgulama yapma sürecinde cevabın öğretmen tarafından hazır şekilde verilmesi ve öğrencinin pasif alıcı şekilde cevabı alması yukarıda tartışılan denge, dengesizlik, uyum ve özümseme-düzenleme süreçlerine aykırı olacaktır. Burada öğrencinin bilgiyi kendisinin yapılandırmasına olanak sunarak ve gerektiğinde ipucu vererek bilginin yapılandırma süreci desteklenmelidir.
Benzer şekilde, öğrencinin dönüşüme uğrayan fonksiyonun $y$ ekseninde hareketini belirlemesinin ardından bu hareketin niceliksel açıklanması ve cebirsel ilişkileri bulması beklenmelidir. Bu durumda öğretmen aşağıdaki gibi sorularla süreçte rehberlik etmelidir:
- Temel fonksiyona ($f(x) = x^2$) göre verilen grafik $y$ ekseni boyunca nasıl bir hareket yapmış olabilir? Neden böyle düşünüyorsun, açıklar mısın?
Temel fonksiyona göre $2$ br aşağıya ötelenen grafiğin denklemine odaklanılarak, öğrencinin nasıl olup da bu hareketin, fonksiyonun denkleminde $f(x) = x^2 – 2$ şeklinde değişikliğe neden olduğunu içselleştirmesi sağlanmalıdır (Şekil 4).
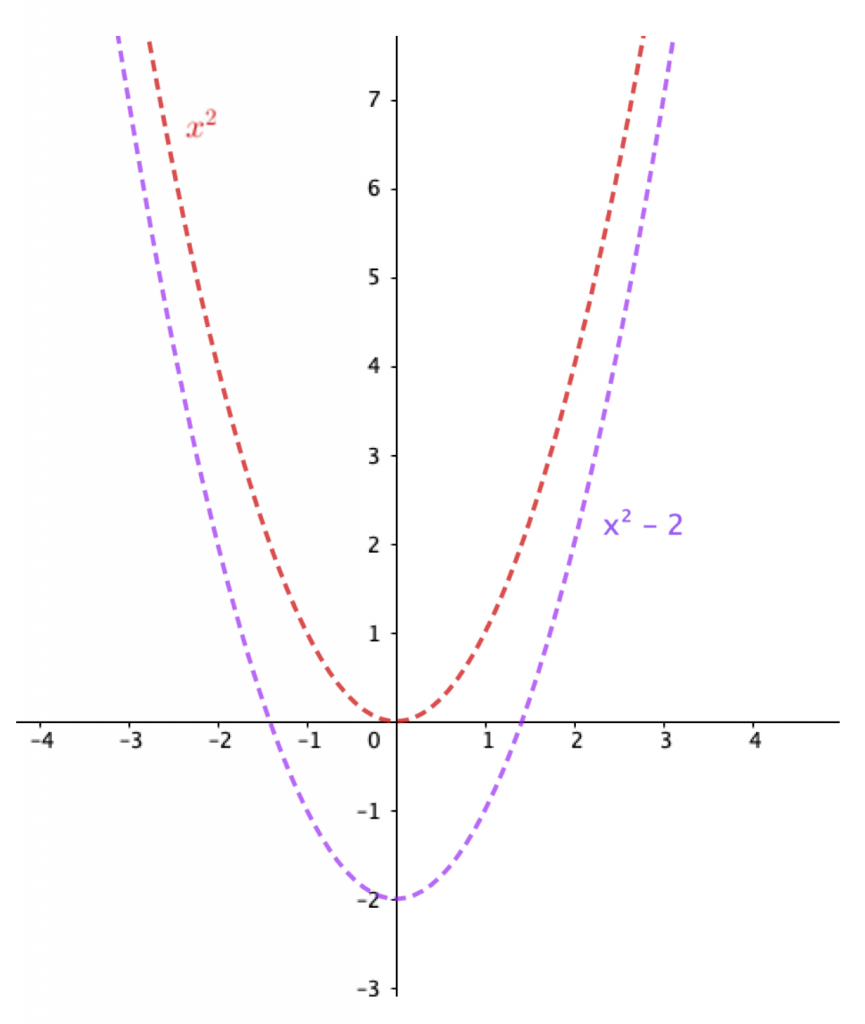
Bu süreçte yönlendirmelerle öğrencinin verilen eğrinin üzerindeki noktalardan yola çıkıp bir noktanın eksenlere göre hareketi ya da dönüşümü ön bilgisini genellemesi beklenebilir. Bu durumda öğretmen, öğrencinin halihazırdaki şemalarına yeni bilgiyi ekleyip genişletmesini sağlayabilir.
Şu ana kadar elde edilen fonksiyon grafiği ($f(x) = (x+3)^2 – 2$) ile formülünün bulunması gereken fonksiyonun grafiği ($f(x) = 2(x+3)^2 – 2$) arasında gözle görülür farklar vardır. Şekil 5’te de görüldüğü gibi öğrencinin bu iki grafik arasındaki farkı belirlemesi ve bu farkın parabolün kollarının daralması/genişlemesi gibi şekillerde tarif edilebilmesi gerekmektedir.
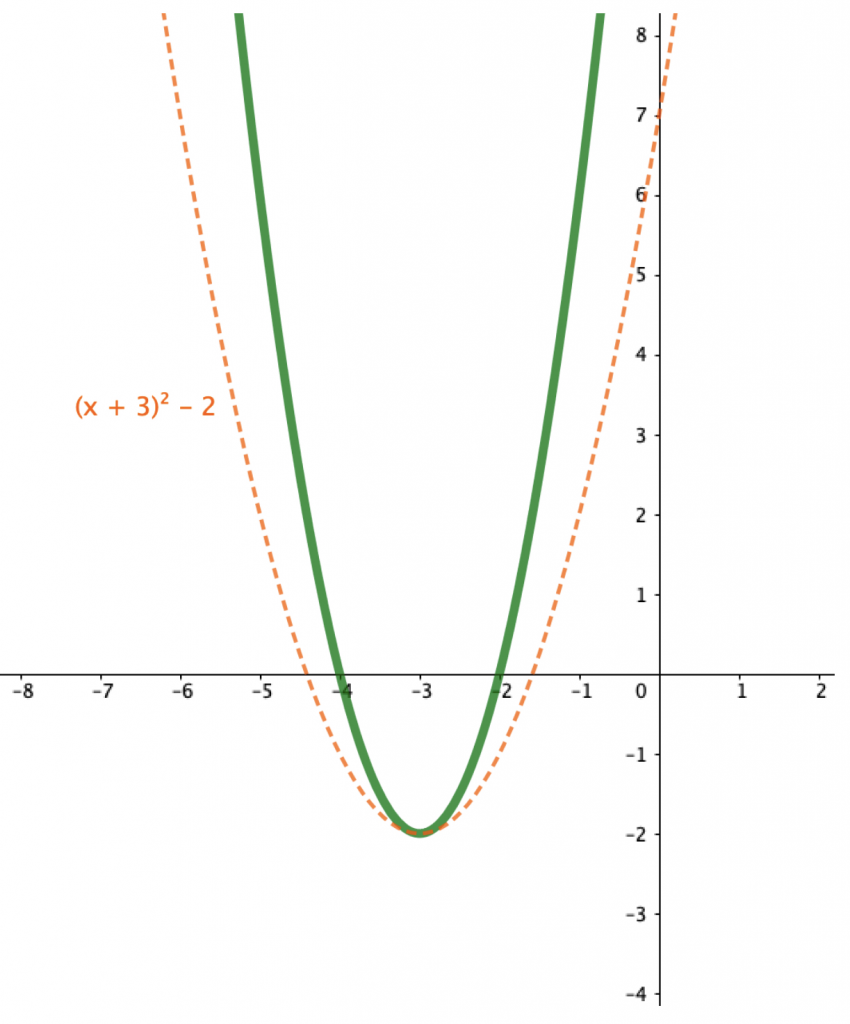
Parabolün kollarının daralması ve ge-niş-le-me-si-ne dair şemaların gelişimi sürecinde, yine temel fonksiyona uygulanan dönüşümün öğrenci tarafından sorgulanması faydalı olacaktır. Bu durum için öğrencinin $f(x) = x^2$ fonksiyonunun grafiğinde kollarının genişlemesi ya da daralması için uygulanacak cebirsel dönüşümü sorgulayıp, bir katsayıyla çarpılması sonucunda meydana gelecek durumu anlamlandırması için yönlendirilmesi gerekmektedir. Aksi takdirde zaman zaman bu durum öğrencinin halihazırda sahip olduğu şemada şöyle yorumlanabilir: “Bir sayının birden büyük bir katsayıyla çarpımı nasıl o sayıyı büyütüyorsa, parabol fonksiyonu 1’den büyük bir katsayıyla çarpılınca kolları ilk haline göre daha geniş görünecektir”. Buradaki anlayışın yer aldığı şema, öğrencinin bir katsayıyla parabolün kollarının daha fazla açılması durumu arasında bir ilişki kurduğunu göstermektedir. Fakat bu doğru bir akıl yürütme değildir. Öğretmen öğrencisinin bir tamsayıyla fonksiyonun çarpılması sonucunda meydana gelen grafiği dinamik matematik yazılımı üzerinden incelemesini sağlayıp, bu durumu sorgulatabilirse tam da bu noktada yeni bilginin inşa sürecinde yukarıda bahsedilen dengesizlik durumu oluşabilir. Diğer bir deyişle, sahip olunan bilgi ile gözlemlenen durum arasında meydana gelen çelişki sayesinde öğrencinin zihninde oluşabilecek dengesizliği ortadan kaldırma sürecinde özümseme ve uyarlama yaparak denge durumunu sağlamak amacıyla dinamik matematik yazılımı kullanabilir. Bu yazılımı kullanırken özellikle grafikte meydana gelen değişikliklere göre öğrenci deneme/yanılma yapıp farklı katsayılarla temel fonksiyon çizerek katsayıya dair genellemeye varabilir (Şekil 6).
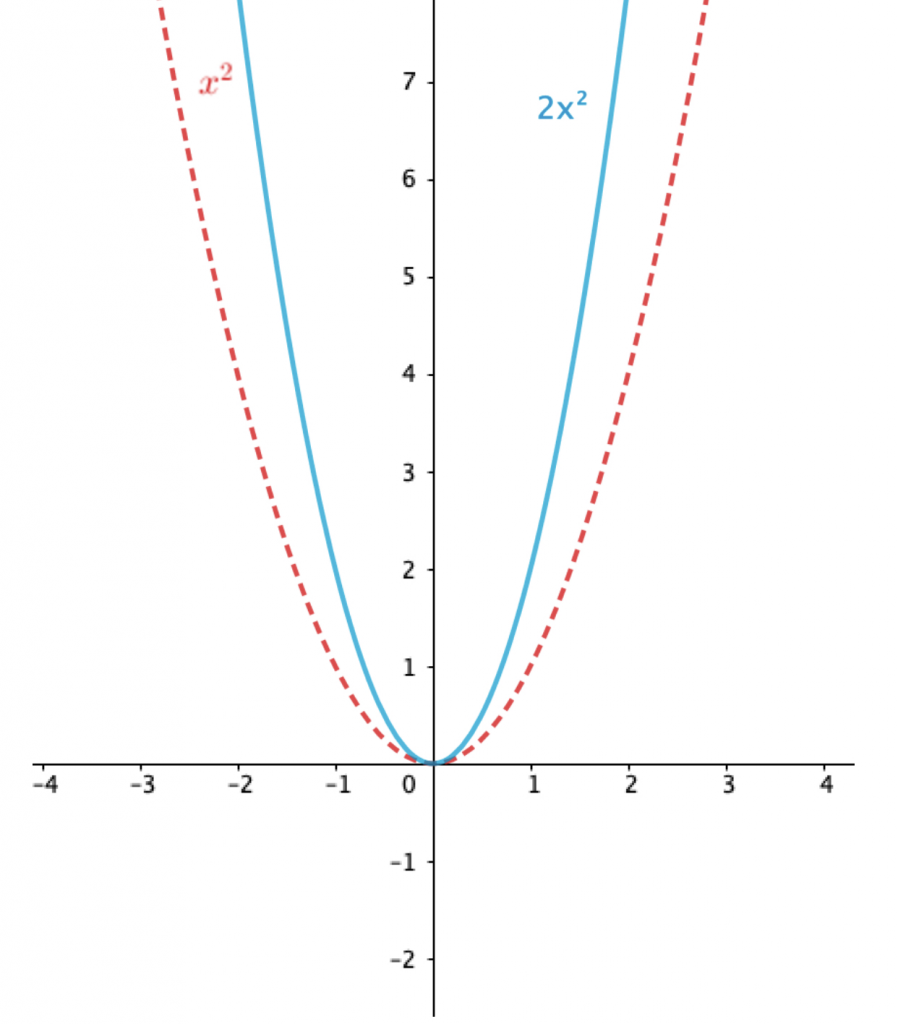
Bu süreçte, bir diğer yöntem olarak, öğrenci aşağıda verilen tablolara benzer tablolar yapıp, $x$ ve $y$ değişkenlerinin aldıkları değerlere göre $x$’in artışı ile $y$’nin artışı arasındaki ilişkiyi keşfederek, bu anlamdaki bilgilerini yapılandırabilir. Öğrenci iki farklı tablodaki $y$ değerlerini karşılaştırarak, fonksiyonun katsayının artmasına bağlı olarak grafiğin $y$ eksenine yaklaştığı (veya $x$ ekseninden uzaklaştığı) veya kollarının daralmasıyla ilgili özümsemeler yapabilir.
| $x$ | $y$ |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| $x$ | $y$ |
| 1 | 2 |
| 2 | 8 |
| 3 | 18 |
Öğrencinin bu sonuca ulaşması için yine öğ-ret-me-nin sorgulayıcı ve gerektiğinde de ipuçları vererek yönlendirici olması gerekmektedir. Öğretmen bu noktada ipucu olarak yine öğrencinin ön bilgisi olan lineer fonksiyon dönüşümlerinden faydalanabilir ve “$f(x) = x$ ve $f(x) = 2x$ fonksiyonlarını göz önünde bulunduralım, bu iki fonksiyonun $y$ eksenine yaklaşması ya da uzaklaşması hali hakkında ne söyleyebiliriz, düşünelim… Peki, şimdi parabol fonksiyonu için bir karşılaştırma yapman gerekirse” gibi ipuçlarıyla bilginin içselleştirilmesini destekleyebilir. Bu iki durum da öğrencinin ilk şemalarında dengesizliğin oluşmasına ortam sağlayabilir böylece hemen ardından şemada düzenleme süreci başlayarak, yeni şemaların oluşturulması ve böylece yeni bilginin oluşumu söz konusu olabilecektir.
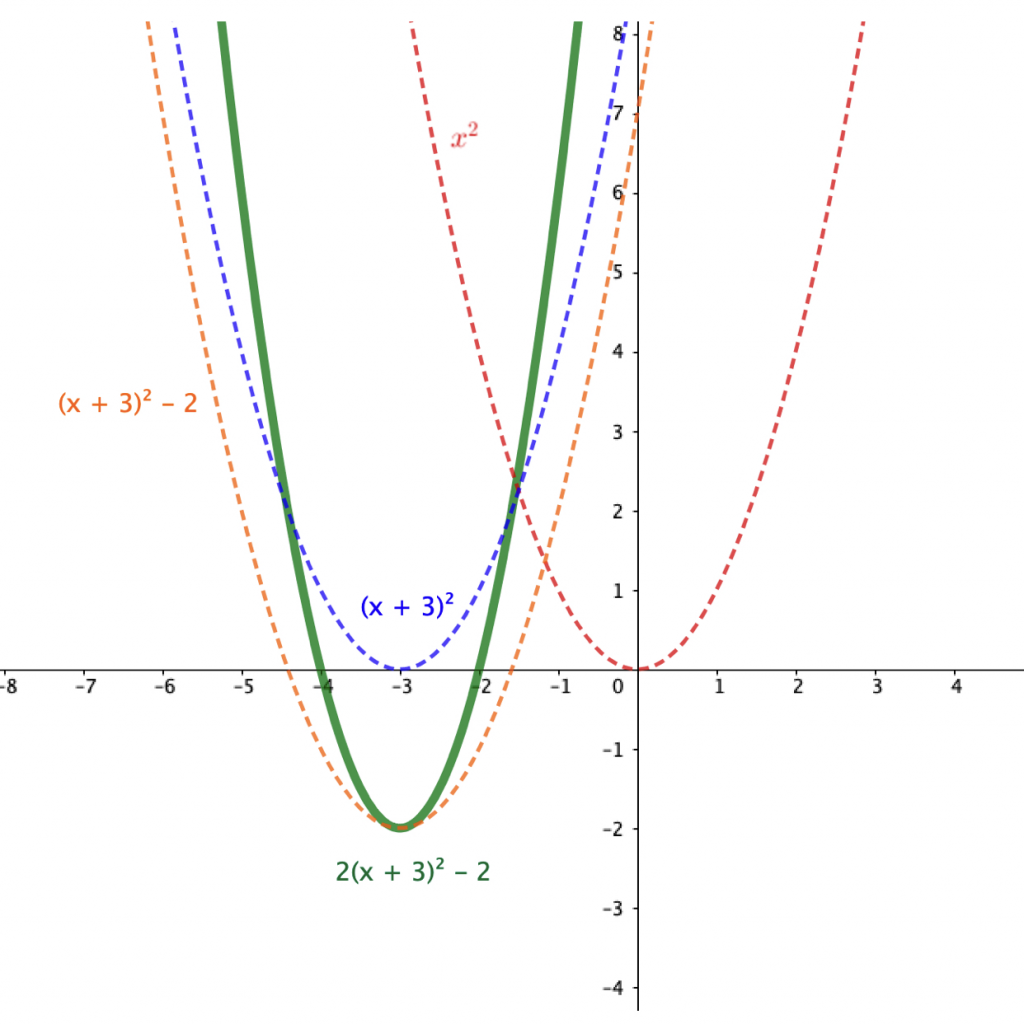
Adım adım tüm bu uygulamalar yapıldıktan sonra, öğrencinin fonksiyon grafiğine karşılık gelen parabol denklemini öteleme yardımıyla bulmaya dair şemaları oluştuğundan (veya revize edildiğinden), istenen denklemin $f(x) = 2(x+3)^2 -2$ olduğunu bulması zor olmayacaktır. Dikkat edilirse, öğrenci burada fonksiyon dönüşümleri konusunun eksenler üzerinde ötelenmesi veya bir katsayıyla çarpılması durumunu anlamlandırmaktadır. Özet olarak Şekil 7’de de gösterildiği gibi, öğrenciler bu noktada fonksiyona, özellikle ikinci dereceden (veya parabol) fonksiyona, dair var olan bilgisiyle öteleme kavramına yönelik bilgisini birleştirip içselleştirerek $f(x) = x^2$ fonksiyonunun $x$ ekseninde 3 birim sola ötelenmesiyle oluşan şekilde, $f(x) = (x+3)^2$ fonksiyonunun denklemini belirleyebilmeye, grafiğini zihninde canlandırabilmeye ve çizmeye dair bilgi oluşumunu yapabilecektir. Aynı şekilde $y$ ekseninde öteleme kavramını düşünerek $f(x) = (x+3)^2 – 2$ fonksiyonuna dair eylemleri gerçekleştirebilecektir. Bu noktada istenen grafiğe yaklaştığını sezen öğrenci kolların durumunu düşünerek $(x+3)^2$’nin katsayısına dair çıkarımlar yapabilme ve istenen denklemi bulabilme yollarını da özümsediğinden ikinci dereceden fonksiyon grafiklerine dair bilgisinin gelişimini destekleyecektir. Özet olarak, bu şekildeki bir uygulamayla öğrencinin mevcut bilgi ve şemaları yeni gelen bilgiye dair yeterli olduğundan sadece özümseme yaparak bu kavramlara/konuya dair var olan şemalarını revize etmiş olacaktır.
Aşağıda fonksiyon dönüşümleri konusunda matematik öğretmenliği programı 3’üncü sınıf öğrencileriyle küçük bir grupta yaptığımız çalışmada yer alan bir öğrencinin, yapılan öğretim öncesinde ve öğretim sırasında parabol fonksiyonuna dair sorulan sorulara verdiği cevaplar yer almaktadır. Öğrenciye öğretim öncesinde Şekil 8’deki gibi $x$ ekseninde öteleme yaparak fonksiyon grafiğini çizmesi istenen bir soru sorulduğunda, grafiği $x$ ve $y$ değişkenlerine değer vererek çizmiştir.
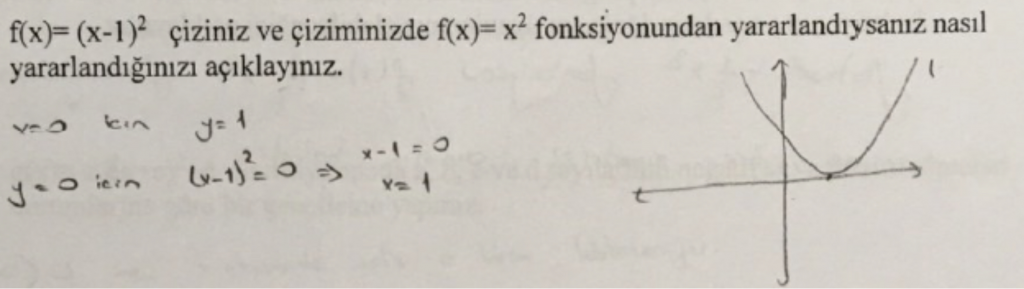
Yukarıda bahsedildiği gibi sırasıyla $x$ ve $y$ eksenlerindeki ötelemeler ve bir katsayıyla çarpımının etkilerinin incelendiği uzun süren dizisel bir uygulama sürecinde, öğrencinin fonksiyon dönüşümleri konusundaki var olan bilgisini revize edip, yeniden yapılandırdığı Şekil 9’daki yapmış olduğu çözümden ve açıklamalarından görülmektedir. Bu uygulamada, öğrencilerin $f(x) = \frac{(x-1)^2}{2} + 1$ fonksiyonunun grafiğini çizmeleri istenmiştir. Bahsi geçen öğrenci uygulama öncesinde gerek denklemi verilip grafiğinin çizimi istenen; gerekse grafiği verilip denklemi istenen fonksiyon dönüşümleri konusunda değişkenlere değer vererek ve halihazırda zihinlerinde yer alan formülü kullanarak çözüm yaklaşımı sergilemesine rağmen, süreçte sorulara yaklaşımı değişmiştir. Şekil 9’da da görülebileceği gibi zihninde tüm öteleme adımlarını hayal edip, kolların temel fonksiyona göre daha geniş olması gerektiğini düşünüp, doğrudan istenen grafiği çizmiştir. Öğretim sırasında bu öğrencinin “benim böyle bir şeyden haberim bile yoktu, ama bu konuyu çok iyi öğrendim şu an” şeklindeki yorumu ve sorulara cevapları öğrencinin var olan bilgisini geliştirdiğine dair kanıt olarak gösterilebilir.

Son olarak, matematik öğretiminde ya-pı-lan-dır-ma-cı yaklaşım temelinde bir öğretim tasarlamak ve öğrencilerinin bilgiyi yapılandırmalarını desteklemek isteyen eğitimciler için aşağıdaki genel çerçevenin göz önünde bulundurulması önerilmektedir. Yapılandırmacı öğrenme teorisinde;
- Öncelikle öğrencilerin bilgiyi özümseyebilmesi için hazır bulunuşluğunun olması gereklidir. Bilişsel olarak hazır olmayan bir öğrenci matematik yapma konusunda başarılı olamayacaktır.
- Bir diğer uyarlamaysa en iyi öğrenmenin aktif katılımla gerçekleşeceği konusudur. Bu katılımda birey sorgulayandır ve zihinsel olarak denge-dengesizlik-uyum ve şema sürecini her konu için deneyimleyebilmesi gerekmektedir.
- Denge-dengesizlik sürecini tetiklemek ve etkili sorgulamalar yapabilmek için somut materyallerin ve sanal manipülatifler ve dinamik matematik yazılımları gibi teknoloji destekli uygulamaların kullanılması önerilmektedir.
- Öğrencilerin gerçek bir kavrayış sağlayabilmeleri için matematiksel kavramları sadece hatırlamakla kalmayıp, bu kavramlar arasındaki ilişkileri anlamaları gerektiği unutulmamalı ve öğrencilerin kavramlar arası ilişkileri kendilerinin oluşturmasını sağlayacak öğrenme ortamları hazırlanmalıdır.
Buraya kadar verilen öneriler Piaget’nin ve onun teorisini kullanan araştırmacıların öğrenmeye dair ortaya koyduğu incelemelere dayanmaktadır. Benzer şekilde bir matematik sınıfında matematiksel kavramların yapılandırılması ve öğrenmenin nasıl gerçekleşmesi gerektiğini inceleyen akademik çalışmalar matematik eğitimiyle uğraşan araştırmacılara farklı öneriler de sunmaktadır. Örneğin, bunlardan birisi “tahmini öğrenme yol haritaları” olup yapılandırmacı yaklaşımın sınıf ortamlarına somut olarak aktarılmasını sağlamak amacıyla Simon [6] tarafından ortaya atılmıştır. Sizler de özellikle fonksiyon dönüşümleri konusunda verilen örnek uygulamayı veya geliştireceğiniz başka bir uygulamayı sınıf içi öğretimlerinize entegre etmek isterseniz öneri okuma listesindeki çalışmaları incelemenizi tavsiye ederiz.
Son olarak, bireylerin öğrenmelerinde hatırlama üzerine kurulu, sonuca odaklı değerlendirmelerin yapılmasını eleştiren Piaget’nin, öğretmenlerin öğrenme ortamlarının rehberleri ve düzenleyicileri olmaları gerektiğini belirttiğini tekrarlamak isteriz [7]. Peki, bu öğrenme ortamlarının aksi nasıl olabilirdi? Bilginin bir bilenden diğer bilmeyen özneye aktarıldığı fikri ya da sürekli tekrarlarla hatırlamaya dayalı süreçlerin bilmeyle eşleştirilmesi ya da anlamsız ezberlenen matematiksel ilişkilerin var olduğu öğrenme ortamlarını bu öğrenme ortamlarına örnek olarak verebiliriz. Bu süreç, bilginin bireyden ve çevreden bağımsız var olduğunu düşündüğünden dolayı bir eğitim-öğretim sürecinden çok egzersiz ve idman yapmaya benzer. Her bireyin kendine özgü inşa ettiği şemaları göz önünde bulundurarak, öğretmenin rehber, öğrencininse bilgiyi aktif olarak yapılandırdığı süreçlerde matematik öğrenme ve öğretme ortamlarını oluşturmanız ve matematik yapmaya büyük bir tutku ile devam etmeniz dileğiyle…
Okuma Listesi
- Clements, D. H., Sarama, J. (2004). Learning trajectories in mathematics education. Mathematical Thinking and Learning, 6(2), 81–89.
- Confrey, J., Maloney, A. P., Corley, A. K. (2014). Learning trajectories: A framework for connecting standards with curriculum. ZDM, 46(5), 719–733.
- Simon, M. (2014). Hypothetical learning trajectories in mathematics education. In S. Leman (Ed.), Encyclopedia of Mathematics Education, pp. 272-275. The Netherlands: Springer.
Kaynaklar
[1] Ernest, P. (1993). Constructivism, the Psychology of Learning, and the Nature of Mathematics: Some Critical Issues. Science \& Education, 2, 87-93.
[2] Piaget, J. (1970). Genetic epistemology. (E. Duckworth, Trans.). London, UK: Routledge \& Kegan Paul Ltd.
[3] Piaget, J., Garcia, R. (1989). Psychogenesis and the history of science. (H. Feider, Trans.). New York, NY: Columbia University Press. (Orijinal eserin basım tarihi 1983).
[4] Beth, E. W., Piaget, J. (1966). Mathematical epistemology and psychology. (W. Mays, Trans.). Dordrecht, Holland: D. Reidel Publishing Company. (Orijinal eserin basım tarihi 1965).
[5] Boz-Yaman, B., Yigit Koyunkaya, M. (2019). Examination of Pre-Service Mathematics Teachers’ Mental Constructions of Function Transformation. Acta Didactica Napocensia, 12(1), 33-56.
[6] Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26(2), 114–145.
[7] Miller, P. H. (2017). Gelişim psikolojisi kuramları. (Çev. Gültekin, Z.; Yay. Haz. Onur, B.) Ankara: İmge Yayınevi. (Orijinal eserin basım tarihi 2007).

