Yazar: Şafak Alpay
Yıl: 1992-5
Sayı: 10
Matematikte varlık teoremleri olarak sınıflandırılan teoremler vardır. $[a,b]$ kapalı aralığında tanımlı, gerçel değerli ve sürekli $f=f(x)$ fonksiyonu bu aralık üzerinde aldığı en büyük değere (maksimum) bu aralığın bir noktasında ulaşır.
Benzer şekilde yukarıda anılan özelliklere sahip $f=f(x)$ fonksiyonu $[a,b]$ aralığında aldığı en küçük değere (minimum) $[a,b]$ aralığının bir noktasında ulaşır.
Sürekli bir fonksiyon için özellikleri olan noktaların varlığını söyleyen bu önermeler varlık teoremleridir.
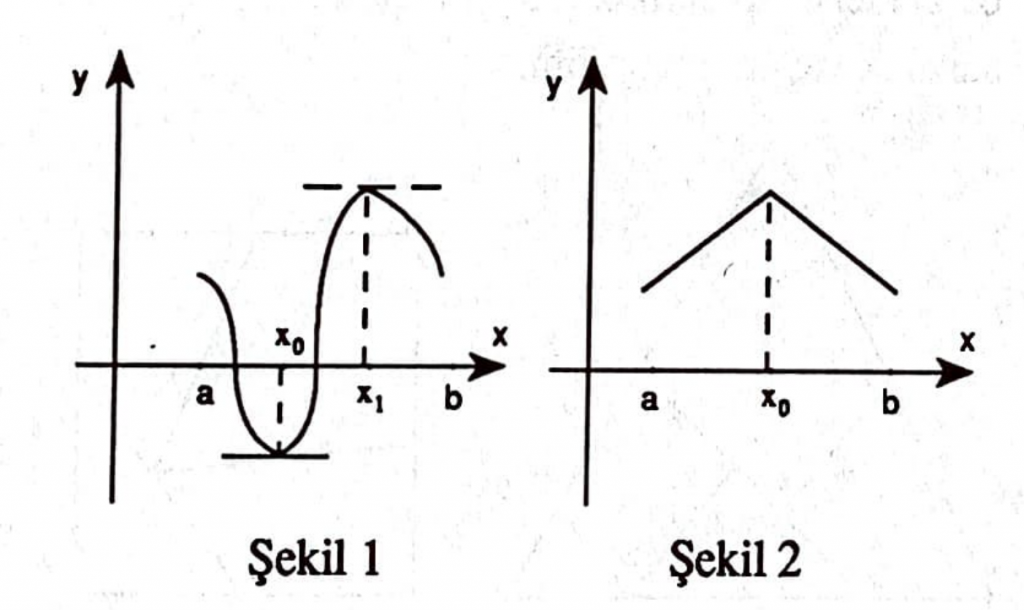
Şekil 1’de grafiği görülen $f= f(x)$ fonksiyonunun minimum değerini aldığı $x_o$, maksimum değerini aldığı $x_1$ noktalarında eğriye çizilen teğet eğimlerinin $0$, başka bir deyişle teğetlerin x-eksenine paralel olduklarını görüyoruz.
Önerme: $x_0 \in [a,b]$, sürekli $f:[a,b] \rightarrow \mathbb{R}$ fonksiyonunun maksimum (veya minimum) değerini aldığı bir nokta olsun. $f, x_0$ noktasında türevlenebilir ise, $x_0\; f’$ (türev) fonksiyonunun bir köküdür, yani $f'(x_0)= 0$ dır.
Kanıt: $f$ fonksiyonunun $x_0$ noktasında türevlenebilir olması
$\lim_{x \rightarrow x_0} \frac{f(x) – f(x_0)}{x- x_0} \qquad \qquad (+) $
limitinin olması demektir. $x_0$ noktasına sağdan yani $x_0$dan büyük değerler boyunca veya $x_0$dan küçük değerler boyunca yani soldan yaklaşılabilir. $(+)$ daki limitin var olması sağ ve sol limitlerin eşitliği ile tanımlanır.
Genellikten kaybetmeden $x_0$ noktasında maksimumun alındığım kabul edebiliriz. $x_0$ noktasına soldan yaklaşırken $x—x_0 \leq 0$ ve $f(x) \leq f(x_0)$ olacağından
$\lim_{x \rightarrow^{-} x_0} \frac{f(x) – f(x_0)}{x- x_0} \geq 0 $ olacaktır. (Niçin?)
$x_0$ noktasına $x_0$dan büyük değerler boyunca yaklaşırken alınan limit
$\lim_{x \rightarrow^{+} x_0} \frac{f(x) – f(x_0)}{x- x_0} \leq 0 $
olacaktır. $f$ fonksiyonunun $x_0$ noktasında türevlenebilir olması
$\lim_{x \rightarrow^{-} x_0} \frac{f(x) – f(x_0)}{x- x_0} = \lim_{x \rightarrow^{+} x_0} \frac{f(x) – f(x_0)}{x- x_0} = \lim_{x \rightarrow x_0} \frac{f(x) – f(x_0)}{x- x_0} = f'(x_0) $
olduğundan, $f'(x_0) \leq 0$ ve $f'(x_0) \geq 0,$ yani $f'(x_0) =0$ olmalıdır.
1652-1719 yılları arasında yaşıyan Fransız matematikçi Michel Rolle çağdaşları Newton ve Leibniz’in yaratıp geliştirdikleri Diferansiyel ve Integral Hesap kuramının karşıtlarından biri olarak ün yapmıştır. Polinomların köklerini araştırırken kanıtladığı aşağıdaki teoremin bu kuramın temel yapı taşlarından biri olması kaderin bir cilvesi herhalde.
Rolle Teoremi: $[a,b]$ üzerinde sürekli, $(a,b)$ üzerinde türevlenebilir olan $f= f(x)$ fonksiyonu $f(a)= f(b)= 0$ koşulunu sağlasın. $(a,b)$ aralığında $f(x_0)=0$ eşitliğini sağlayan $x_0$ noktası vardır.
Kanıt: $f$ sabit $0$ fonksiyonu ise teorem açıktır. Aksi halde $f(x)$ fonksiyonunun maksimum değerini aldığı noktayı $x_1$, minimum değerini aldığı noktayı $x_2$ ile gösterelim. $f(a)= f(b)= 0$ olduğundan $x_1$ veya $x_2$den biri $(a,b)$ içinde olmalıdır.
Teoremlerin hipotezleri olan varsayımları düşünmemizde yarar vardır. Örneğin, Şekil 2’de grafiği verilen fonksiyonun neden Rolle Teoremine bir çelişki olmadığını ve $[—1,1]$ aralığında $f(x)= |x|-1$ olarak tanımlanan fonksiyonu düşünerek teoremdeki türevlenebilirlik varsayımdan vazgeçilemiyeceğini görmeliyiz.
Rolle Teoreminin aşağıdaki sonucu aynı anda ipi göğüsleyen iki atletin hızlarının yarış süresince en az bir kez eşit olması gerektiğini söylüyor!
Sonuç: $f_1$ ve $f_2, [a,b]$ aralığında sürekli, $(a,b)$ aralığında türevlenebilir fonksiyonlar ve $f_1(a) = f_2(a), f_1(b)= f_2(b)$ olsun. $(a,b)$ aralığında $f’_1(x_0) = f’_2(x_0)$ denklemini sağlayan bir $x_0$ sayısı vardır.
Kanıt: Sürekli ve türevlenebilir fonksiyonların farkları da aynı özellikleri taşır! $(a,b)$ aralığındaki her $x$ için $f(x)= f_1(x)- f_2(x)$ ile tanımlanan fonksiyon Rolle Teoreminin koşullarını sağlar ve istenileni verir.
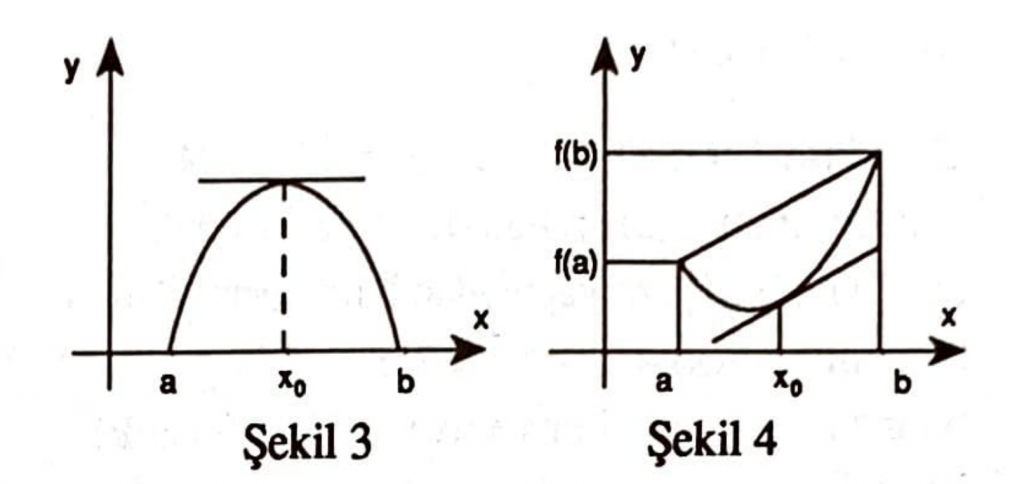
Rolle Teoremi $x_0 \in (a,b)$ için eğriye $(x_0, f(x_0))$ noktasında çizilen teğetin x—eksenine paralel olduğunu söylüyordu. (Şekil 3). Fransız matematikçisi Joseph Louis Lagrange (1736-1813) tarafından kanıtlanan Ortalama Değer Teoremi benzer koşullarda bir $x_0 \in (a,b)$ için $(x_0, f(xo))$ noktasında çizilen teğetin (Şekil 4), $(a, f(a))$ ve $(b, f(b))$ noktalarını birleştiren doğruya paralel olacağını söylüyor.
Ortalama Değer Teoremi (ODT): $f = f(x)$ fonksiyonu $[a,b]$ aralığında sürekli, $(a,b)$ aralığında türevlenebilir olsun. $(a,b)$deki bir $x_0$ sayısı için
$f'(x_0) = \frac{f(b)-f(a)}{b-a}$
sağlanır.
Kanıt: $[a,b]$ aralığındaki her $x$ için
$g(x) = f(a) + (x-a) \Big[\frac{f(b)-f(a)}{b-a} \Big]$
ile tanımlanan $f$ ve $g$ fonksiyonları sonuçtaki hipotezleri sağlar. Dolayısı ile $(a,b)$ içindeki bir $x_0$ için
$f'(x_0) = g'(x_0) = \frac{f(b)-f(a)}{b-a}$
elde edilir.
$f(x) = |x|$ fonksiyonunun $[-1,1]$ aralığında, $h(x) = \tan x$ fonksiyonunun $[0,\pi]$ aralığında, $g(x) = x-\lfloor x \rfloor$ fonksiyonunun $[0,1]$ aralığında ODTnin hipotezlerini sağlamadığını görmeliyiz. Verilen fonksiyonlar için belirtilen aralıklarda ODT doğru mu?
Uygulamalar:
1) $4x^3 -27x^2 +52x -24$ polinomunun $(0,2)$ aralığında en az bir kökü olduğunu hiç işlem yapmadan bulabiliriz. Çünkü bu polinom $f(x) = x^4 -9x^3 + 26x^2 -24x$ polinomunun türevidir ve $f(0)=f(2)=0$ vardır. Polinomlar türevlenebilir olduklarından istenilen Rolle Teoreminden elde edilir.
2) $f(x) = \sqrt{x}$ fonksiyonunu $[100,101] $ aralığında düşünerek $\sqrt{101}$ sayısını yaklaşık olarak bulabiliriz. ODTden $100<m<101$ olan bir $m$ sayısı için
$\frac{\sqrt{101}-\sqrt{100}}{101-100} = \frac{1}{2\sqrt{m}}$ veya
$\sqrt{101} = 10 + \frac{1}{2\sqrt{m}}$
elde ederiz. $10< \sqrt{m}< \sqrt{101}\;$ bize $\;20<2\sqrt{m}<2\sqrt{101}= \sqrt{404} = 21$ ve
$\frac{1}{21}< \frac{1}{2\sqrt{m}}< \frac{1}{20}$ verir. Dolayısı ile $\sqrt{101}$in, $10 + \frac{1}{21}$ ve $10+ \frac{1}{20}$ arasında bir sayı olduğunu söyleyebiliriz.
3) Eğer $f$ in türevi $f’$ fonksiyonunun $[a,b]$ aralığında aldığı minimum değer $m,$ maksimum değer $M $ ise ODT’den $(b-a)m < f(b)-f(a) < (b-a)M$ elde edilir. Bu eşitsizliği $f(x)= \sin x$ fonksiyonu için kullanarak her $a,b$ için $|\sin b – \sin a| < |b — a|$ elde edebiliriz.
ODT giderek artan otoyollarımız üzerinde hız denetimi yapmak için kullanılabilir. $f=f(t)\; t$ birim zamanda alınan yolu göstersin. $f=f(t)$nin türevlenebilir olduğunu varsayarsak, $f'(t)$ bize $t$ anındaki hızı verecektir.
4) Son model BMW i ile saat 12.01 de Ankara-İstanbul otoyoluna giren Bay HIZLI saat 12.46 da 120 km ötedeki Gerede çıkış turnikesine girer. Bilete bakan memur, Bay Hızlı’nın şaşkın bakışları arasında Trafik polisini çağırır. Polis, Hızlı’nın karşı çıkışlarına rağmen, ODT gereğince
$\frac{f(3/4)-f(0)}{\frac{3}{4}} = \frac{120-0}{\frac{3}{4}} = 160 = f'(c)$
denkleminden Hızlı’nın saat 12.01 ile 12.46 arasında 160 km/saat hız yaptığını söyliyerek gerekli cezayı keser.
Yazımızı yanıtlarını beklediğimiz sorular ile bitirelim.
- $f$ bir polinom olsun $a$ ve $b$ sayılan $f$ in ikişer kez kökü olduğu sayılar ise, $f’$ nün $[a,b]$ aralığında en az üç kökü olduğunu gösterebilir misiniz?
- $f$ ve $g\; [a,b]$ aralığında tanımlı, türevlenebilir fonksiyonlar olsunlar. $[a,b]$ deki her $x$ için $f'(x)= g'(x)$ ise, bir $c$ sayısı için $g(x)= f(x) + c$ olduğunu gösterebilir misiniz?
- $a< b$ koşulunu sağlayan $a$ ve $b$ sayıları arasında $m^2 = \frac{1}{3}(b^2 +ab+a^2)$ eşitliğini sağlayan $m$ sayısının varlığını gösterebilir misiniz?
- $(0,1)$ aralığı içinde $\tan x= 1 — x$ denklemini sağlayan bir noktanın varlığını kanıtlayınız.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Umut Gür‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

