Yazar: Cemal Koç
Yıl: 1992-1
Sayı: 6
Bu sayımızda Emre Alkan’ın derlediği problemlere devam edeceğiz. Ancak bunlar geçen sayıdakilere göre daha fazla ön bilgi gerektiriyor. Bütünlük sağlamak için önce Cemal Koç’un “Bir üçgene ait çemberler” konulu yazısına yer verdik.
Bir üçgene ait çevrel çember, dış teğet çemberler ve dokuz nokta çemberi üçgenin ögelerindendir. Bu yazıda amacımız, gerekli ön bilgilerle birlikte söz konusu çemberlere ilişkin bazı önemli özellikleri sunmak.
Kolaylık sağlamak için yazımız boyunca sık sık kullanacağımız gösterimleri verelim:
, , açılar ve açı ölçüleri
, , kenar orta noktaları
, , açı ortayların karşı kenarları kesim noktaları
, , yükseklik ayakları
ortosantr, ağırlık merkezi, çevrel çember merkezi
; , , iç ve dış merkezler
dokuz nokta çemberinin merkezi
, , kenar uzunlukları
, , kenarortaylar
, , açıortay uzunlukları
, , yükseklikler
alan, yarı çevre
çevrel yarıçap
, , , iç ve dış yarıçaplar
Stewart Teoremi ve Sonuçları
Stewart teoremi bir üçgene ait kenarortay açıortay vb. ögelerin uzunluk formüllerini hemen verebilen kullanışlı bir sonuç.
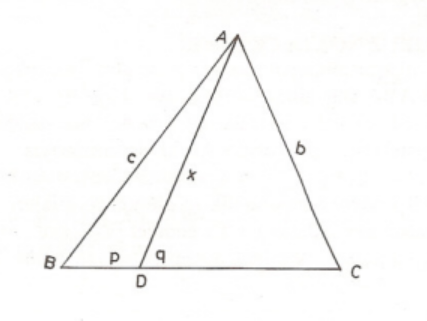
Teorem 1: (Stewart) Bir üçgeninin kenarı üzerinde bir nokta olsun. Eğer ise olur.
İspat: ve açılarının ölçülerine sırasıyla ve diyerek ve üçgenlerine kosinüs teoremini uygularsak elde ederiz. Birincinin her iki yanını , ikincisininkini ile çarpıp toplarsak ispat biter.
Bu teoremde alacak olursak kenarortay uzunluğunu verir. Açıortay uzunluğunu bulmak için ise açıortay bağıntısı adı verilen
eşitliklerini kullanmak yeterlidir. Buna göre şu sonucu verebiliriz:
Sonuç: Bir üçgeninin köşesine ilişkin kenarortay ve açıortay ise
(kenarortay bağıntısı)
(2)
(3)
(4)
olur. Şimdi üçgenlerdeki çemberleri tek tek ele alalım.
Çevrel Çember
Bir üçgeninin köşelerinden geçen tek bir çember vardır;
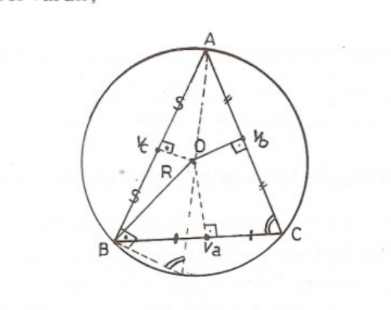
Merkezi kenar orta dikmelerin kesim noktası olan bu çembere çevrel çember diyoruz. Aşağıdaki bağıntılar yazılabilir:
(Sinüs Teoremi)
(5)
(6)
Teğet Çemberler
Bir üçgeni için, her üç kenara da teğet olan dört çember vardır. Doğal olarak bu çemberlerin merkezleri iç ya da dış açıortayların kesim noktalarıdır. İki iç açıortay üçgen içinde, iki dış açıortay da üçgen dışında keseceklerinden bu dört çemberden birinin merkezi üçgen içinde, diğer üçünün karşılık geldikleri köşeye göre , , ile gösterilen merkezleri üçgen dışındadır. Benzer biçimde yarıçaplar için de , , , gösterimleri kullanılır. Buna göre , , köşelerinden
(i) iç çembere olan teğet uzunlukları sırasıyla , ,
(ii) merkezli dış çembere olan teğet uzunlukları , ,
olur.
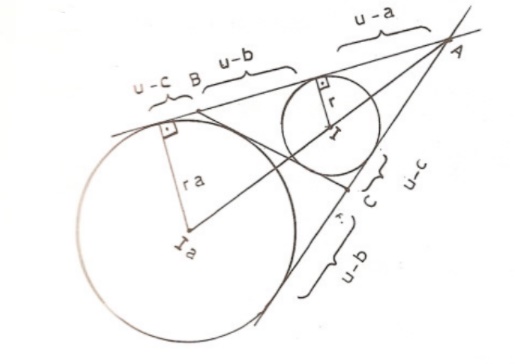
Böylece hemen şu sonuçları yazabiliriz:
(7)
(8)
Alıştırmalar
1) ve bağıntılarını kurunuz.
2)İç teğet çemberin ’ye değme noktası ise, olduklarını göstererek bağıntısını kurunuz.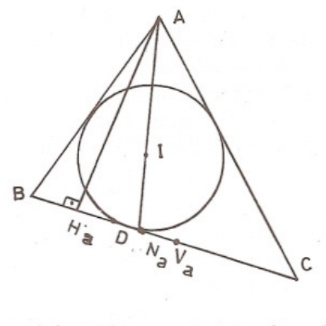
3) üçgeninin açıortayı çevrel çemberi noktasında keserse
olduğunu gösteriniz.
Dokuz Nokta Çemberi
Bir üçgeninin ortosantırını köşelere birleştiren doğru parçalarının orta noktaları sırasıyla , , olsun. Açı hesaplamalarıyla , , , , , noktalarından her birinin doğru parçasını dik açı altında gördükleri kolayca gerçeklenebilir. Bu çember ve çaplı çemberlerle aynıdır. Öyleyse dikme ayakları, kenar orta noktaları ve , , ’den oluşan dokuz nokta bir çember üzerindedir. Bu çembere dokuz nokta çemberi, Euler çemberi ya da Feuerbach çemberi denir.
Dokuz nokta çemberinin merkezi ’ın orta noktası ve yarıçapı ’dir. Önce yarıçapın olduğunu görelim. Bunun için benzeşim oranıyla oluşunu düşünmek yeterli. ’nın orta noktası olan merkezini belirlemek için ise şu saptamaları yapalım:
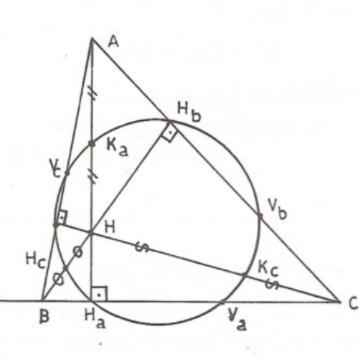
(a) ve
Demek ki noktası üçgeninin ortosantrıdır.
(b) ve ’dir yani noktası üçgeninin ortosantrıdır. ile eş olduklarından
elde edilir. Böylece hem dörtgeninin paralelkenar olduğunu hem de kendi başına da önemli olan
(9)
bağıntısını elde etmiş oluruz. Bu paralelkenarın köşegeninin ortası ’nın orta noktasıdır.
Euler Doğrusu
Şimdi ve doğrularının kesim noktalarına diyelim.

(9) uyarınca olduğundan noktası ’nin ağırlık merkezi yani ’dir. Demek ki noktası üzerinde olup eşitliği sağlanır. Böylece , , , ’nin doğrudaş olduklarını görmüş bulunuyoruz. Bu noktaların üzerinde bulunduğu doğruya Euler doğrusu denir. Aşağıdaki şekilde bu noktaların Euler doğrusu üzerindeki konumları görülmektedir.
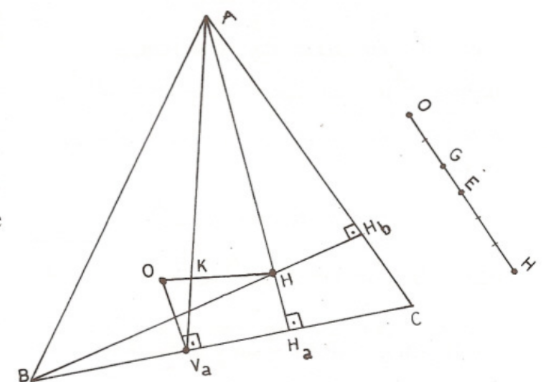
Vektörel bir yazışla,
(10)
Euler Teoremi
Önce şu teoremle işe başlayalım:
Teorem: Bir üçgeninin açıortayı çevrel çemberi noktasında keserse aşağıdaki bağıntılar doğrudur:
(i)
(ii) (11)
İspat: Açılara bakacak olursak,
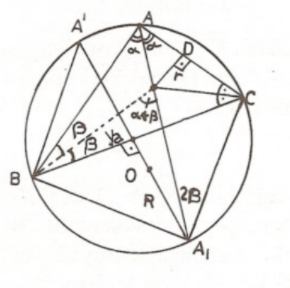
olup ’nin ikizkenarlığı çıkar. Benzer biçimde ikizkenardır. İkinci kısım için ise ’in çevrel çemberi kestiği diğer noktaya diyerek, elde edilir.
Artık çevrel çember merkezinin iç ve dış merkezlerden olan uzaklıklarını veren Euler teoremini ele alabiliriz.
Teorem: (Euler) Bir üçgeninin çevrel çember merkezi ile iç merkezi ve dış merkezi arasındaki uzaklıklar eşitlikleri ile belirlidir.
İspat: Şekil 9’u kullanacak olursak, ’nın üzerindeki dik izdüşümü olmak üzere ’den çıkar. Yukarıdaki teoremden yazarsak ve ’nın çembere göre kuvvetini ya da Stewart Teoremini kullanırsak elde ederiz. Böylece ve sonuç olarak istenen bağıntısı çıkar.
Dış teğet çember için ispatı okura bırakıyoruz.
Bazı Geometrik Eşitsizlikler
Euler teoreminin çok açık bir sonucu eşitsizliği. Burada eşitliğin olabilmesi için ile ’nın çakışması yani üçgenin eşkenar üçgen olması gerekir ve yeter. Şimdi bu ana eşitsizliği ve bundan elde edilen bazı eşitsizlikleri verelim.
Sonuç: Bir üçgeni için aşağıdaki eşitsizlikler geçerlidir. Bu eşitsizliklerde eşitlik durumunun olması için üçgenin eşkenar olması gerekir ve yeter.
1) (13)
2) (14)
3) (15)
4) (16)
5) (17)
6) (18)
İspat:
1) Açık.
2) Aritmetik – Geometrik ortalama eşitsizliğinden ’dan istenen elde edilir.
3) (13) ve (14)’ten dolayı, çıkar ve birinci eşitsizlik elde edilir.
4) (11) ve (13)’den hemen çıkar.
5) oluşu nedeniyle (16) isteneni verir.
6) (17)’den
5’ten 3’ün ikinci bir kanıtını verebiliriz:
eşitliğini kullanacak olursak olur. Şimdi (18) eşitsizliğinden elde edilir. Oysa oluşunu kullanırsak elde edilir ve (15)’teki ikinci eşitsizlik gösterilmiş olur. Eşitlik durumlarını irdelemeyi okura bırakıyoruz.
Alıştırmalar: Aşağıdaki eşitsizlikleri gösteriniz:
1)
2)
3)
4)
Feuerbach Teoremi
Konunun bütünlenmesi açısından Feuerbach teoremi zorunlu. 1800 ve 1834 yılları arasında yaşayan ve Almanya’nın Erlangen kentinde lise öğretmenliği yapan Feuerbach 1822’de yayımladığı bir kitapçıkta üçgenlere ait çemberlerle ilgili birbirinden güzel birçok bağıntı vermiş. Bunların en ilgi çekeni kendi adıyla anılır olmuş.
Teorem: (Feuerbach) Dokuz nokta çemberi iç çembere ve dış çembere teğettir.
İspata girmeyip ilgilenen okura Cem Tezer’in gelecek sayımızdaki yazısını önereceğiz.
Son olarak iki soru:
1. (1991 Olimpiyatı) Verilen bir üçgeninde iç çemberin merkezi olsun. , , açılarının iç açıortaylarının karşı kenarları kestikleri noktaları sırasıyla , , ile gösterelim. Aşağıdaki eşitsizliğin doğru olduğunu gösteriniz.
2. bütün kenarları farklı uzunlukta bir üçgen, üçgenin ağırlık merkezi, iç merkez ve ortosantr ise olduğunu gösteriniz.
Kaynaklar:
– R. A. Johnson, Modern Geometry, Houghton Mifflin Company 1929.
– L. S. Shively, An Introduction to Modern Geometry, John Wİley and Sons, Inc. London 1939.









