Yazar: Hüseyin Demir
Yıl: 1991-5
Sayı: 5
Macar matematikçisi Paul Erdös (1913) ve ünlü eşitsizliği ile tanışmam, Columbia Üniversitesi Bölümü’nün son sınıfında bulunduğum 1944 yılına rastlar. Kendisiyle bir matematik toplantısında tanıştırıldım. Tahtaya geçip bir üçgen çizerek içinde bir nokta aldı ve tam ifadesi aşağıda verilen eşitsizliğini benden ispatlamamı istedi. Problemi ilginç bulduğum için ispatlamaya çalıştımsa da başarılı olamadım. Çalışmam yan bir ürün verdi. Onu 1944’te bir dergide yayınladım. Sonraları ün yapmış olan bu eşitsizliğin bir ispatını vermiş olmayı ne kadar isterdim.
TEOREM (ERDÖS). ABC bir üçgen ve $P$ bunun içinde ya da üzerinde bir nokta olsun, $P$nin köşelerinden olan $R_1, R_2, R_3$ uzaklıkları ve kenarlardan olan $r_1, r_2, r_3$ uzaklıkları
$$R_1 + R_2 + R_3 \geq 2 (r_1 + r_2+r_3)$$
eşitsizliğini sağlar ve eşitlik ancak üçgen eşkenar ve $P$ merkezinde olduğunda geçerlidir.
Bu teorem ilk kez bir tahmin olarak 1935 yılında American Mathematical Monthly dergisinde yayınlanmış ve ilk ispatı 1937 yılında Mordell tarafından verilmiştir. Bu nedenle bugün eşitsizlik Erdös-Mordell Eşitsizliği olarak tanınmaktadır. Bu eşitsizliğin üç ispatını aşağıda bulacaksınız. Kanımca bunlardan en güzeli Kazarinoff tarafından verilen III. ispattır.
ISPAT I (Leon Bankoff, 1958). $\overset{\triangle}{ABC}$ içinde alınan $P$ noktasının $BC,$ $CA$ ve $AB$ kenarları üzerindeki izdüşümleri sırasıyla $D, E$ ve $F$ noktaları olsun.
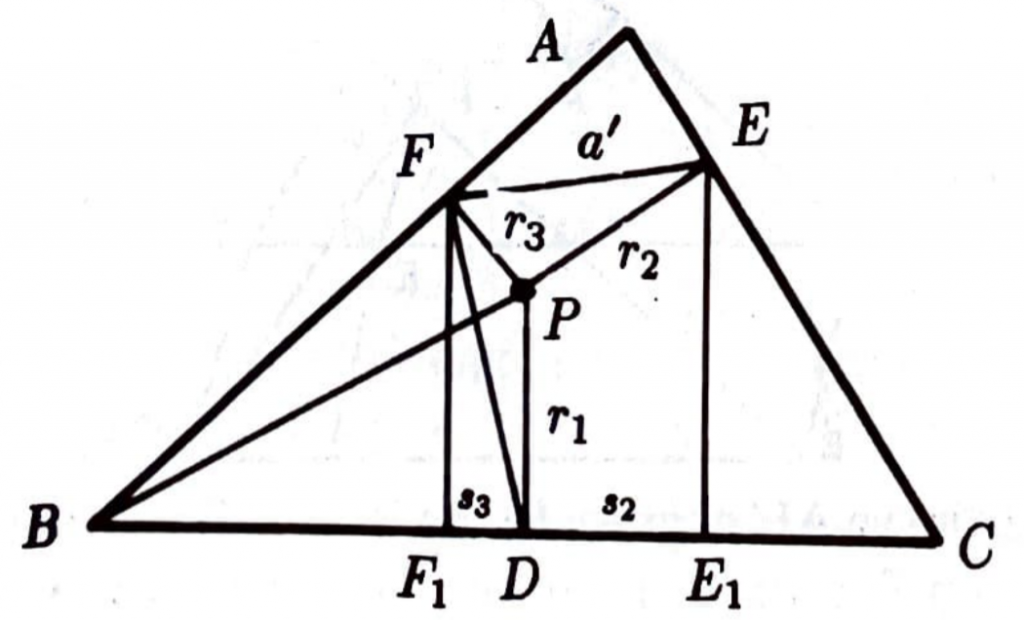
Şekildeki gibi,
$|PD| =r_1, |PE| = r_2, |PF| =r_3,$
$|EF|= a’, |FD|=b’, |DE| = c’,$
$|PA| = R_1, |PB| = R_2, |PC| = R_3$
diyelim.
E ve F noktalarının $BC$ üzerindeki dik izdüşümlerine sırasıyla $E_1$ ve $F_1$ deyip yazış kolaylığı için $|F_1D| =s_3, |E_ID| =s_2$ koyalım. FBDP dörtgeni kirişler dörtgeni olduğu için
$ m(\widehat{FBP}) = m(\widehat{FDP}) = m(\widehat{DFF_1)}$
elde edilir ve $\overset{\triangle}{DFF_1} \sim \overset{\triangle}{PBF}$ olduğu görülür. Buradan
$$s_3 = \frac{b’}{R_2}r_3 $$
ve benzer biçimde
$$ s_2 = \frac{c’}{R_3}r_2$$
çıkar. Demek ki $|FE| \geq |F_1E_1|$ oluşunu ve diğer izdüşümleri düşünürsek
$1 \geq \frac{1}{a’}\Big(\frac{b’}{R_2}r_3 + \frac{c’}{R_3}r_2 \Big) $
$1 \geq \frac{1}{b’}\Big(\frac{c’}{R_3}r_1 + \frac{a’}{R_1}r_3 \Big) \qquad \qquad (1)$
$1 \geq \frac{1}{c’}\Big(\frac{a’}{R_1}r_2 + \frac{b’}{R_2}r_1 \Big) $
elde edilir. Bunları sırasıyla $R_1, R_2, R_3$ ile çarpıp toplayarak yeni bir düzenleme ile
$R_1 + R_2 + R_3 \geq r_1 \Big( \frac{R_2c’}{R_3b’} + \frac{R_3b’}{R_2c’} \Big) $
$\qquad \qquad \qquad + r_2 \Big( \frac{R_3a’}{R_1c’} + \frac{R_1c’}{R_3a’} \Big) \qquad \qquad (2)$
$\qquad \qquad \qquad + r_3 \Big( \frac{R_1b’}{R_2a’} + \frac{R_2a’}{R_1b’} \big)$
buluruz. Oysa parantez içlerinden her biri $x + 1/x$ biçiminde olup
$$x + \frac{1}{x} -2 = \frac{x^2-2x+1}{x} = \frac{(x-1)^2}{x}$$
eşitsizliği nedeniyle
$$x + \frac{1}{x} \geq 2 \qquad \qquad (3)$$
dir. Bunun (2)de kullanılması ile istenen
$$R_1 + R_2 + R_3 \geq (r_1 + r_2 + r_3) \qquad \qquad (4)$$
eşitsizliği elde edilir.
Şimdi eşitliğin hangi durumda olacağını inceleyelim. Üçgen eşkenar ve P merkez nokta ise eşitliğin olacağı açık. Karşıt olarak, (4)’te eşitlik ancak (1), (2) ve (3)’te eşitlik varsa mümkündür. Bu ise
$EF//BC, FD//AC, DE//AB \qquad \qquad (5)$
$\frac{R_2c’}{R_3b’} = \frac{R_3a’}{R_1c’} = \frac{R_1b’}{R_2a’}= 1 \qquad \qquad (6)$
olması demektir. (5)’ten, örneğin ABCB paralelkenarını kullanırsak $|BA| = a’ = |DC|$ elde ederiz yani $D$ ve benzer şekilde $E$ ile $F$ kenarların orta noktalarıdır. Yani $P, \overset{\triangle}{ABC}$nin çevrel çember merkezidir. $R_1 = R_2 = R_3$ olduğunda (6)’dan $a’ = b’ = c’$ ve dolayısıyla $a= b=c$ elde edilir, yani üçgen eşkenardır.
ISPAT II. (L.J. Mordell, 1937) P’nin ABC’ye göre ayak üçgeni DEF ve bunun kenar uzunlukları $a’,b’,c’$ olsun (İspat I’deki şekil).
AEPF kirişler dörtgeni ve sinüs teoreminden
$$R_1= \frac{a’}{\sin{A}} \qquad \qquad (7) $$
bulunur. PEF’ye uygulanan kosinüs teoreminden ise
$a^{‘2} = r_2^2 + r_3^2 + 2r_2r_3 \cos A$
$= r_2^2 + r_3^2 -2r_2r_3 \cos(B+C)$
$= r_2^2 + r_3^2 – 2r_2r_3 (\cos B\cos C – \sin B\sin C)$
$= (r_2\sin C + r_3 \sin B)^2 + (r_2\cos C- r_3\cos B)^2 $
$\Rightarrow a^{‘2} \geq (r_2\sin C + r_3 \sin B)^2$
$a’ \geq (r_2 \sin C + r_3 \sin B) \qquad \qquad (8)$
ABC’nin kenar uzunlukları $a,b,c$ ise (1)den
$R_1 \geq \frac{\sin C}{\sin A}r_2 + \frac{\sin B}{\sin A}r_3$
$\Rightarrow\; R_1 \geq \frac{c}{a}r_2 + \frac{b}{a}r_3 \qquad \qquad (9)$
elde olunur. Eşitlik hali ancak
$$r_2 \cos C – r_3 \cos B =0 $$
iken var olup $AP | BC$ olacağı gösterilebilir. (3) eşitsizliği benzer olarak $R_2$ ve $R_3$ için yazılırsa
$$R_2 \geq \frac{a}{b}r_3 + \frac{c}{b}r_1$$
$$R_3 \geq \frac{b}{c}r_1 + \frac{a}{c}r_2$$
elde olunur. Bu üç eşitsizlik taraf tarafa toplanırsa
$$R_1 + R_2 + R_3 \geq \Big(\frac{b}{c} + \frac{c}{b} \Big)r_1 + \Big(\frac{c}{a} + \frac{a}{c} \Big)r_3 \qquad \qquad (10)$$
bulunur. Eşitlik, ancak, $AP | BC, BP | CA, CP | AB$ iken yani P ortosantr olduğunda vardır.
Şimde, $x,y>0$ için
$$\frac{x}{y} + \frac{y}{x} \geq 2 \qquad\qquad (*) $$
eşitliğini kullanalım. Bu, $(x-y)^2 \geq 0$a denk olup doğrudur ve eşitlik ancak $x=y$ iken vardır. O halde (4)ten
$$R_1 + R_2 + R_3 \geq 2(r_1 + r_2 + r_3) $$
elde edilir ve eşitlik ancak P noktasının ortosantr ve ABC’nin eşkenar olması halinde geçerlidir.
ISPAT III. (D.K. Kazarinff, 1957) P’nin A köşesine ait iç açıortayına göre simetriği P’ olsun. P’ACC’ ve P’ABB’ paralelkenarlarını
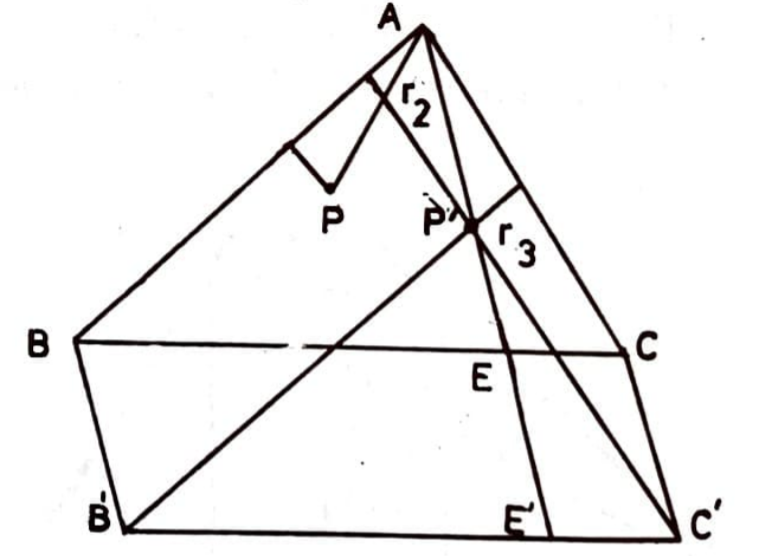
çizelim ve $AP’$ doğrusu $BC$ ve $B’C’$ yü $E$ ve $E’$ de kessin. Paralelkenarların alanları ile ilgili olarak $$|P’ACC’|+|P’ABB’|=|ECC’E’|+|BB’E’E|=|BCC’B’|\leq|BC||CC’|=aR_1$$ elde olunur ve
$$br_3+cr_2\leq aR_1$$
$$\Rightarrow R_1 \geq \dfrac{c}{a}r_2+\dfrac{b}{a}r_3$$
çıkar. Eşitlik ancak $CC’|BC$ iken yani $AP|BC$ olduğunda geçerlidir.
Bir $ABC$ üçgeninde H ortosantr ve O çevrel merkez ise $\angle HAC=\angle OAB$ olduğu bilindiğinden, $AP$ doğrusu $O$dan geçmiş olur.
$R_1$ için elde edilen eşitlik $R_2$ ve $R_3$ için yazılıp üç eşitsizlik taraf tarafa toplandığında
$$R_1+R_2+R_3 \geq (\dfrac{c}{b}+\dfrac{b}{c})r_1+(\dfrac{a}{c}+\dfrac{c}{a})r_2)+(\dfrac{b}{a}+\dfrac{a}{b})r_3$$
bulunur ki (*)dan
$$R_1+R_2+R_3 \geq 2(r_1+r_2+r_3)$$
elde olunur. Eşitlik ise ancak $ABC$ eskenar ve $P$ çevrel merkezi olduğunda geçerli olur.
Erdös’inkine benzer eşitsizlikler
Matematikçilerde benzetme ya da genelleme il bir teoremden başka teoremler elde etme eğilimi vardır. Durum, konumuz olan eşitsizlik için de geçerlidir. Söz gelimi,
$$R_1+R_2+R_3\geq2(r_1+r_2+r_3) $$ (1)
yazılışındaki toplamların simetrik fonksiyonlar oluşumu gözönüne alan $A$. Oppenheim $R_1,R_2,R_3$ ve $r_1,r_2,r_3$ün simetrik fonksiyonlarıyla çeşitli eşitsizlikler kurmuştur. Bunların üçünü verelim:
$$R_2R_3+R_3R_1+R_1R_2 \geq 4(r_2r_3+r_3r_1+r_1r_2)$$ (2)
$$R_1R_2R_3 \geq 8r_1r_2r_3$$ (3)
$$\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3} \geq (\dfrac{1}{r_1}+\dfrac{1}{r_2}+\dfrac{1}{r_3})$$ (4)
Bunların ispatını öğrenmek isteyenler Kaynak kitabına başvurabilirler.
Öte yandan Macar matematikçisi Fejes Toth (1) eşitsizliğini n-genlere genelleyerek (5) i elde etmiştir.
$$R_1+R_2+\cdots+R_n \geq (sec\dfrac{\pi}{n}(r_1+r_2+\cdots+r_n)$$ (5)
Bunun n=3 için özel hali (1)dir.
(1)in uzayda bir genellemesi neden olmasın? Dörtyüzlüler için şu tahmini yapamaz mıyız?
$$R_1+R_2+R_3+R_4 \geq 3(r_1+r_2+r_3+r_4)$$ (6)
Bu tahmin yanlış da çıkabilir.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Umut Gür‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

