Yazarlar: Özgür Özlük, Ayşegül Şahin, Cem Tezer
Yıl: 1991-3
Sayı: 3
İsmi, bu yazının konusunu teşkil eden teoremden ayrılmaz halde bulunan Pisagor hakkında çok az şey biliniyor. Sahanın temkinli mütehassıslarının ([2] gibi) eleğinde kalan sağlam delillerin sayısı o kadar az ki, Pisagor’un ciddi bir ilim adamı mı yoksa siyasete meraklı bir şaman mı, arkasında bıraktığı derneğinse halis niyetleri olan bir akademi mi yoksa varlığı biraz batıl itikadlara hatta biraz da terörizme dayalı bir tarikat mı olduğunu belki hiçbir zaman öğrenemeyeceğiz. Bu mecrada diğer bir zorluk da bugün alim, filozof, din adamı, politikacı diye adlandırdığımız insanların çalışma sahaları arasındaki sınırların, Pisagor’un çağı olan M.Ö. 6. yüzyıla doğru bir zaman yolculuğunda hızla değişip, bulanıklaşmasıdır.
Pisagor’un ve takipçilerinin kim, insanlığa hizmetlerinin de ne olduğu sorusunda en mühim yer Pisagor teoremi olarak anılan ve bir dik üçgende dik kenarların uzunluklarının kareleri toplamının, hipotenüsün uzunluğunun karesine eşit olduğunu söyleyen teoreme aittir. Günümüzde Pisagor teoreminin başta Çin medeniyeti olmak üzere dünyanın büyük medeniyetlerinde çok eskiden beri bilinmekte olduğu ortaya çıkıyor. [5]
Teoremin ilk ispatının Pisagor tarafından yapıldığına dair bir delil yok. Bilinen en eski ispatıyla birlikte teorem Euclid’in “Elemanlar”ının birinci kitabında 46. önerme olarak bulunuyor. Bu kitap hakkında yazdığı değerli şerhte Proclus, daha o devirde (Pisagor’dan 10 yüzyıl sonra) Pisagor’un hayatına dair birçok efsane olduğunu işaretle, kanaatince Euclid’in bu ispatı bulmakla hayranlık duyulmaya Pisagor’dan daha layık olduğunu söylüyor. [4]
Bugün elimizde Pisagor teoreminin yüzlerce ispatı var. [3] Burada size birkaç örnek sunmak istiyoruz.
I
Sade veya zarif değilse bile, tarihi önemi ve tabiiliği yüzünden Euclid’in ispatını öncelikle ele alalım (Şekil 1):
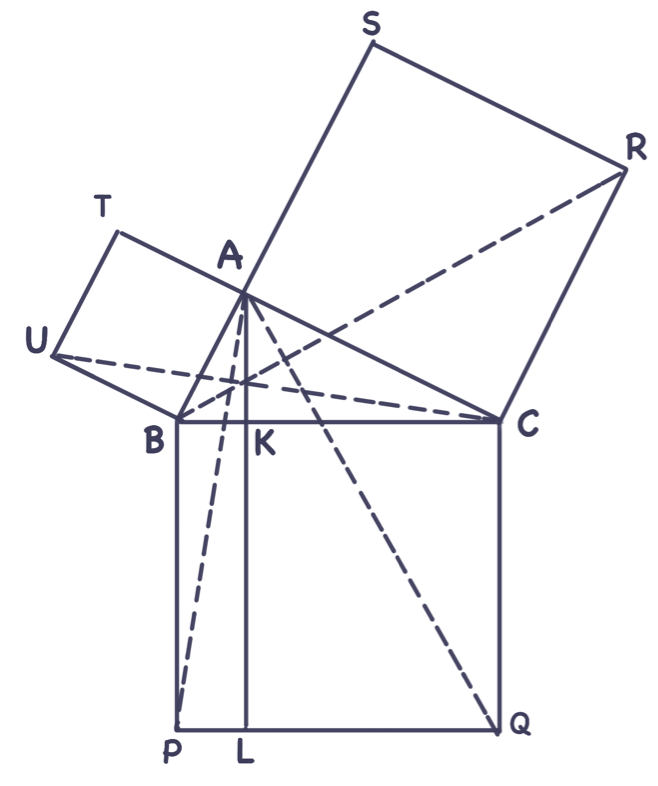
$ABC$ dik üçgeninde, sırasıyla $AB$ ve $AC$ dik kenarları üzerine kurulan $BATU$ ve $ACRS$ kareleri ile $BC$ hipotenüsü üzerine kurulan $PQCB$ karesini gözönüne alalım. $A$ dan $BC$ ye indirilen dikme $BC$ yi $K,PQ$ yu da $L$ noktasında keserek, $PQCB$ karesini $PLKB$ ve $LQCK$ dikdörtgenlerine ayırsın. Okuyucu $UBC$ üçgeninin $ABP$ üçgenine denk olduğunu kolayca gösterebilir. $BATU$ karesi alanca $UBC$ üçgeninin, $PLKB$ dikdörtgeni de alanca $ABP$ üçgeninin iki katına eşit olduğuna göre, $BATU$ karesinin alanı $PLKB$ dikdörtgeninin alanına eşit olmalıdır. Aynı şekilde $ACRS$ karesinin alanının da $LQCK$ dikdörtgenin alanına eşit olduğu gösterilebilir. Demek ki $BATU$ ve $ACRS$ karelerinin alanları toplamı $PQCB$ karesinin alanına eşit olmalıdır.
II
Euclid’in ispatı, temel fikir muhafaza edilerek daha sade bir şekle sokulabilir (Şekil 2): Gene $BATU$ ve $ACRS$ sırasıyla $AB$ ve $AC$ dik kenarları üzerinde kurulmuş karaler, $BCQ’P’$ ise $BC$ hipotenüsünü kenar kabul edip $A$ noktasını da içinde bulunduracak şekilde yerleştirilmiş kare olsun.
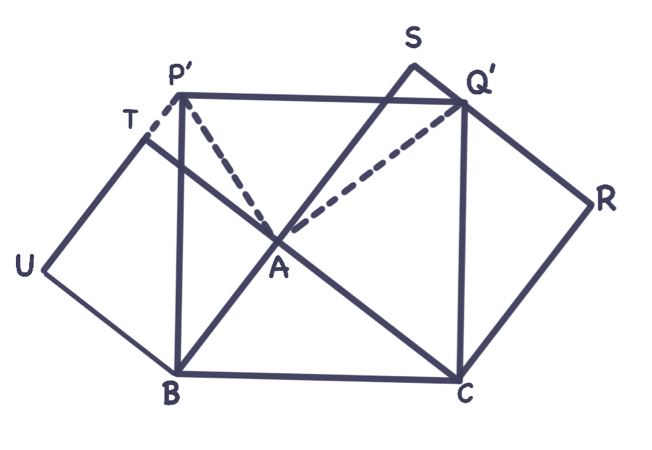
$P’$ ve $Q’$ noktaları sırasıyla $UT$ ve $RS$ doğruları üzerinde kalacaktır (!). $BATU$ ve $ACRS$ kareleri alanca sırasıyla $P’BA$ ve $Q’AC$ üçgenlerinin iki katı olup, bu üçgenler de beraberce $BCQ’P’$ karesinin alanca yarısını teşkil etmektedirler.
III
Okuyucumuzun gözü artık alanları değiştirmeden şekilleri değiştirmeye alışmış olmalıdır. Euclid’in ispatının daha da sade bir şeklini kendisi Şekil 3’ten yararlanarak elde edebilir. Biz sadece $BCQ’P’$ nün Şekil 2’den tanıdığımız kare olduğunu hatırlatmak ve $BAZP’, ACQ’Z$ paralelkenarlarının alanca sırasıyla $AB, AC$ dik kenarları üzerine kurulmuş karelere eşit olduklarına işaret etmekle yetiniyoruz.
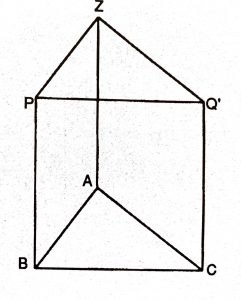
IV
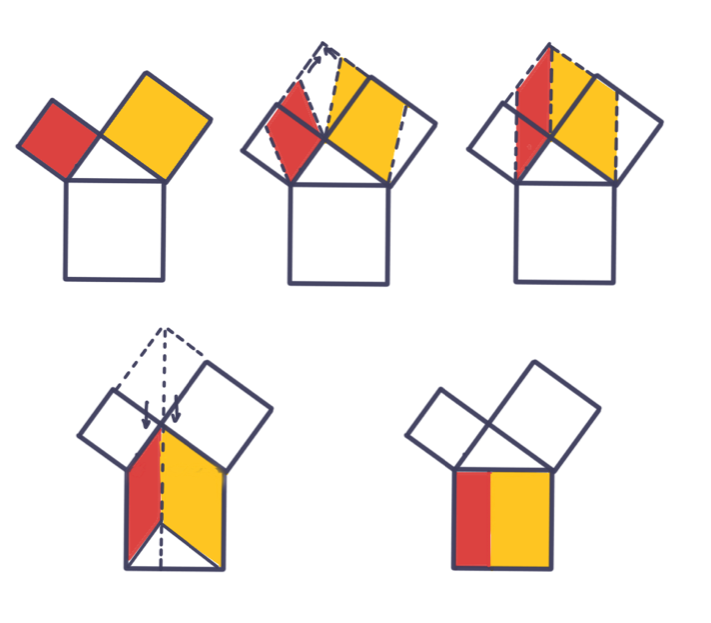
Kareleri alanları değişmeden paralelkenarlara çevirme fikrinden faydalanarak Pisagor teoreminin ispatı bir çizgi film haline getirilebilir (Şekil 4, [1]).
V
Pisagor teoreminin en zarif ispatlarından birisi de Hintli matematikçi Bhaskara’ya (M.S. 12. yüzyıl) izafe edilen ve gelenek olarak muhatabı sadece şekle bakmaya davet etmekten ibaret olan ispattır. Biz de okuyucumuzu Şekil 5’te Bhaskara’nın manevi huzuruna davet ediyoruz.
VI
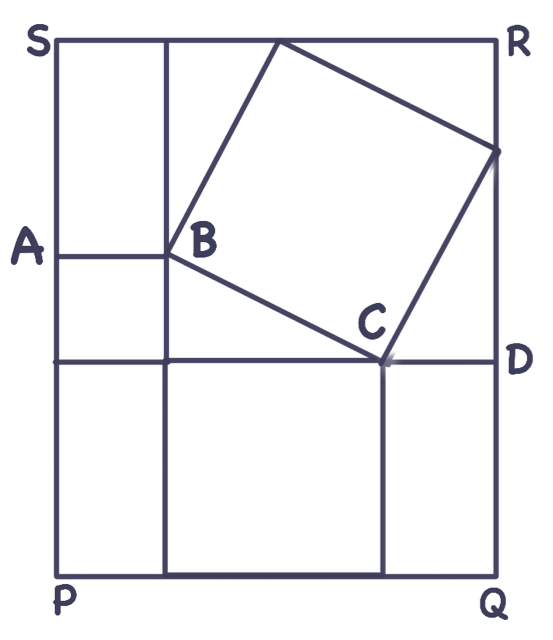
“Peki, sizce hangisi en zarif?” denilse, bu metnin yazarlarının ittifakla seçecekleri ispat H. Demir’e ait ispat olur (Şekil 6). Üstadın 19?? Darüşşafaka’da ortaokul öğrencisiyken bulduğu bu ispat hakkında bütün söylemek istediğimiz $ABCD$ kırık çizgisinin $PQRS$ dikdörtgenini denk iki parçaya ayırdığı. Gerisi okuyucuya ait! Bhaskara’ya layık bir rakip değil mi?
VII
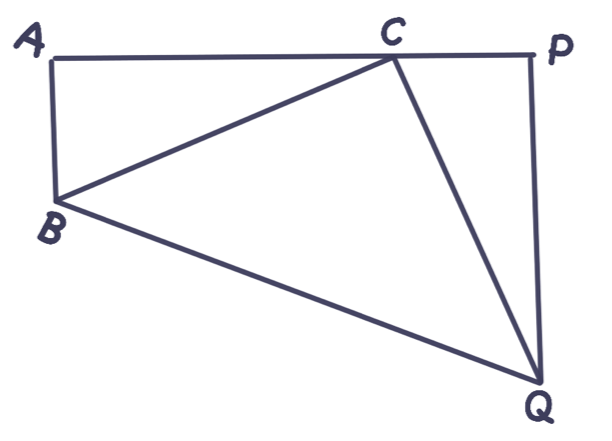
Pisagor teoremi tarih boyunca sayısız amatörü ilgilendirmiş. Bunlar arasında ikbal merdiveninde çok yükselerek tırmanmış bir kişi de var: 1881’de Amerika Birleşik Devletleri Başkanı seçildikten dört ay sonra bir suikaste kurban giden J.A. Garfield. Garfield’in ispatı Şekil 7’de görüldüğü gibi $ABC$ dik üçgenine, bu üçgene denk bir $PCQ$ dik üçgeni eklenerek elde edilen $BQPA$ dik yamuğunun alanını iki farklı şekilde hesaplayarak yapılıyor: $a =|BC|, b= |CA|, c=|AB|$ yazarsak $BQPA$ dik yamuğunun alanı bir taraftan $\frac{(b + c)^2}{2}$ bir taraftan da üçgenlerin alanlarının toplamı olarak $\frac{bc}{2} + \frac{a^2}{2} + \frac{bc}{2}$ şeklinde yazılabilir. Basit bir hesap, hepimizin aşinası olduğumuz $a^2 + b^2 = c^2$ yi verecektir. Garfield’in birinci sınıf bir beyne sahip olduğu belli. O beyni taşıyan başın siyaset gibi nafile bir uğraşta verilmiş olması ne acı!
VIII
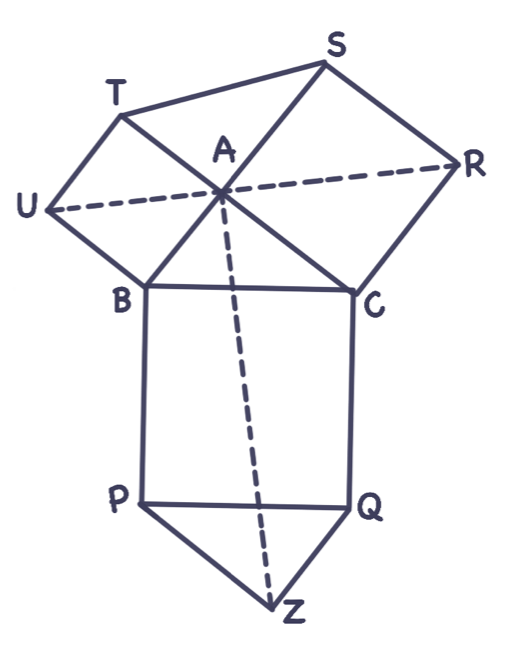
Dörtgenlerin denkliğine dayalı olduğu için buraya kadarkilerden tarz itibariyle ayrılan çok güzel diğer bir ispatla devam ediyoruz (Şekil 8). $ABC$ dik üçgenini ve Şekil l’den tanıdığımız karelerini alalım. $A$ noktasının $PQCB$ karesinin merkezine göre bakışığına $Z$ diyelim. $ABPZ, ZQCA, TURS, UBCR$ dörtgenleri birbirlerine denktir (!). Böylece $TUBCRS$ ve $ABPZQC$ altıgenleri alanca eşit olmalıdır. Bu altıgenlerden ilki dik kenarlar üzerindeki kareler ve ABC üçgeninin iki nüshasından meydana gelir; ikincisi ise hipotenüs üzerindeki kare ile gene $ABC$ üçgeninin iki nüshasından!
IX
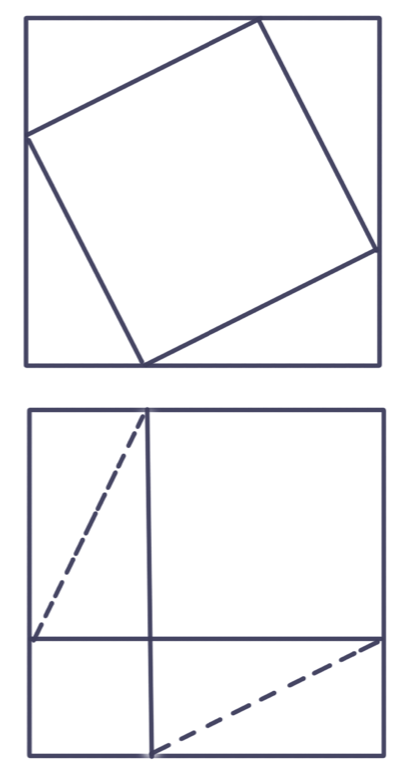
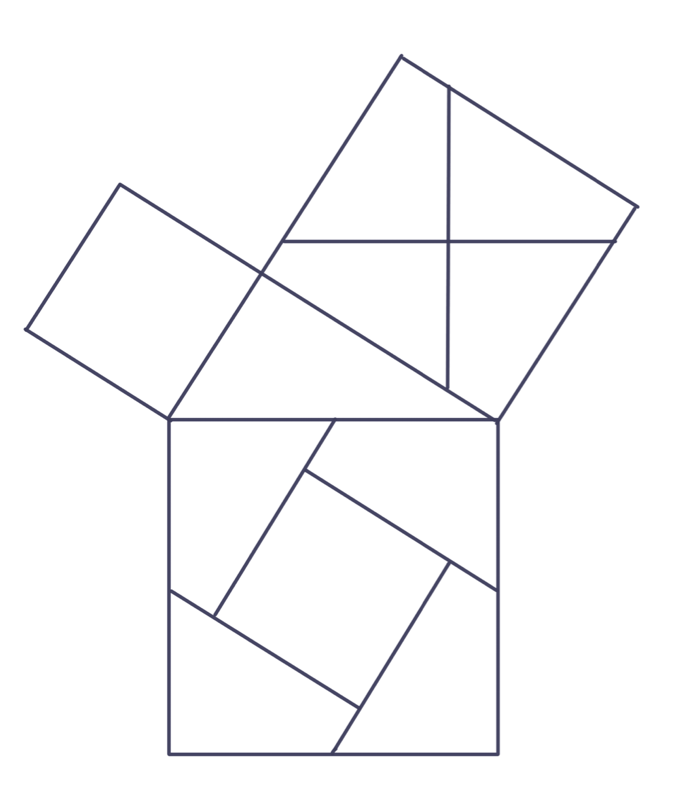
Pisagor teoreminin yüzlerce ispatından birçoğu eşparçalama tekniklerine dayanır. Bildiklerimizden en güzelini Şekil 9’da sunuyoruz. Eşparçalamanın nasıl yapıldığını şu ipuçları tespit edecektir: a) Eşparçalama sadece dik üçgenin kenarlarına paralel veya dik doğru parçalarıyla gerçekleştiriliyor. b) Büyük dik kenar üzerindeki kareyi bölen doğru parçaları karenin merkezinde kesişiyorlar.
Dik üçgenlerde kenar uzunlukları arasında yukarıda söz konusu edilen ilişkiyi, yani Pisagor teoremini çeşitli şekillerde ispat etmiş olduk. Fakat uygulamaların büyük bir kısmında, kenar uzunlukları arasında bu ilişki varsayılıp, bundan üçgenin dik üçgen olduğuna hükmedilir. Yani aslında uygulamada önemli olan “Bir $ABC$ üçgeninde $<BAC = \pi/2$ olması için gerek ve yeter şart $|BC|^2 = |AB|^2 + |CA|^2$ olmasıdır” önermesidir. Halbuki Pisagor teoremi bu önermenin ancak gerek şart kısmım teşkil eder. Birçok geometri kitabında eksik kalan bu hususa temas ederek, yani Pisagor teoreminin tersini ispatlayarak, yazımızı noktalıyoruz:
Bir $ABC$ üçgeninde $|BC|^2 = |AB|^2 + |CA|^2$ varsayalım. $|PQ| = |AB|, |RP| =|CA|$ ve $<QPR=\pi /2$ olacak şekilde bir $PQR$ dik üçgeni alalım. Pisagor teoreminden dolayı $|QR|^2 = |PQ|^2 + |RP|^2 = |AB|^2 + |CA|^2 =|BC|$ böylece de $$IQRI = PCI$$ bulunur. Kenar-kenar-kenar denklik teoremine göre $ABC$ üçgeni $PQR$ üçgenine denk olup
$$<BAC = <QPR = \pi/2$$
dir.
Kaynaklar
[1] L.N.H. Bunt, P.S. Jones, J.D. Bedient: “The Historical Roots of Elementary Mathematİcs”, Dover Publications, New York 1988.
[2] J. Burnet: “Early Greek Philosophy”, 4. Edisyon Adam and Charks Black, Londra 1971.
[3] E. Fourrey: “Curiositos Geometriques”, 4. Edisyon Librairie Vnİbert, Paris 1938.
[4] Proclus: Commentary on the First Book of Euclid’s Elements”, Önsöz ve notlarla İngilizceye çeviren: Glenn R. Morrow, Princeton University Press, Princeton, New Jersey 1970.
[5] F.J. Swetz, T.l. Kao: “Was Pythagoras Chinese? An Examİnatİon of Right Triangle Theory in Ancient China”, The Pennsylvania State University Studies, no. 40.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 3. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

