Yazar: Ali Doğanaksoy
Aşağıdaki karenin hanelerine 1’den 9’a kadar olan sayılar öyle yerleştirilmiştir ki, her satırın, her sütunun ve iki köşegenin üzerinde yer alan sayıların toplamı daima 15’e eşittir. Bu özelliği ile bu kareye, bir “3’lü sihirli kare” diyoruz.
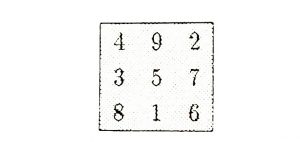
Bu ifadeyi genelleştirerek satırları, sütunları ve köşegenleri toplamı hep aynı sayıya eşit olacak şekilde hanelerine 1’den \(n^2\)’ye kadar sayıların yerleştirildiği, kenarı \(n\) hanelik bir kareyi de \(n\)’li sihirli kare olarak tanımlarız. Örneğin, aşağıdaki 9’lu sihirli karede sabit toplam 369’dur.
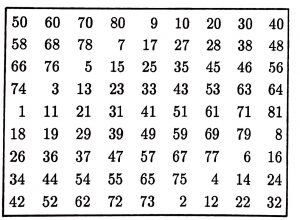
Bir \(n\)’li sihirli karede 1’den \(n^2\)’ye kadar olan bütün sayılar birer kere yazıldığı için bütün hanelerin toplamı \(\frac{n^2 (n^2 + 1)}{2}\) dir. O halde \(n\) satırdan her birinin toplamı da \(\frac{n^2 (n^2 + 1)}{2 n} = \frac{n^3 + n}{2}\) olarak elde edilir. Yani, \(n\)’li bir sihirli karenin sabit toplamı \(\frac{n^3 + n}{2}\) dir. Nitekim, \(n = 3\) için \(\frac{n^3 + n}{2} = \frac{27 + 3}{2} = 15\) ve \(n = 9\) için de \(\frac{n^3 + n}{2} = \frac{729 + 9}{2} = 369\) olduğu görülmektedir.
Lo-shu adı verilen \(\begin{smallmatrix}4 & 9 & 2\\3 & 5 & 7\\8 & 1 & 6\end{smallmatrix}\) karesi çok eskiden beri büyük alaka toplamıştır. Mistik özelliklere sahip olduğu bile düşünülen lo-shu, günümüzde dahi Uzak Asya ve Hindistan’da karşımıza çıkabilmektedir. Antik çağlardan günümüze kadar sihirli karelerle o kadar uğraşılmıştır ki, ortaya bir sihirli kareler kültürü çıkmıştır. Günümüze oranla o zamanlar haklarında bilinenler çok az olmasına rağmen, 1838 yılında Fransa’da bu konuda üç ciltlik bir çalışma yayınlanmıştır. Bu alana ilgi gösterenler arasında Arthur Cayley, Oswald Veblen gibi matematikçilerin adları verilebilir.
Şimdi şu soruya cevap arayalım: Acaba lo-shu‘dan başka 3’lü sihirli kare var mıdır? Elbette vardır. Örneğin, lo-shu‘yu merkezi etrafında \(90^{\circ},\, 180^{\circ}\) veya \(270^{\circ}\) döndürmekle sihiri bozulmaz ama aşağıdaki sihirli kareler elde edilir…

Aynaların sayıların toplamı üzerinde bir etkisi olmadığına göre, lo-shu‘nun ve dönmüş lo-shu‘ların aynadaki akisleri de hep sihirli olacaktır yani,
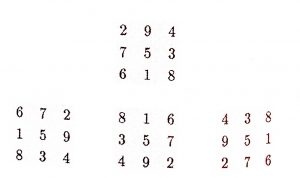
kareleri de hep sihirlidir. Şimdi elimizde tam sekiz tane 3’lü sihirli kare oldu. Acaba başka var mı? Hayır… Bunu şöyle gösterebiliriz: 1’den 9’a kadar sayıların içinden toplamı 15 olan üç sayıyı sekiz şekilde seçebiliriz: \(\begin{smallmatrix}(1 & 5 & 9)\end{smallmatrix}, \begin{smallmatrix}(1 & 6 & 8)\end{smallmatrix}, \begin{smallmatrix}(2 & 4 & 9)\end{smallmatrix}, \begin{smallmatrix}(2 & 5 & 8)\end{smallmatrix}, \begin{smallmatrix}(2 & 6 & 7)\end{smallmatrix}, \begin{smallmatrix}(3 & 4 & 8)\end{smallmatrix}, \begin{smallmatrix}(3 & 5 & 7)\end{smallmatrix}, \begin{smallmatrix}(4 & 5 & 6)\end{smallmatrix}\). 3’lü sihirli karede de üzerindeki sayılar toplamı 15 olması gereken tam sekiz eleman vardır: üç satır, üç sütun ve iki köşegen. Karenin merkezindeki hane bir satır, bir sütun ye iki köşegen üzerindedir; o halde buraya yazılacak sayı listede en az dört seçenekte görülmelidir. Bunu sağlayan tek sayı da 5 olduğu için sihirli karenin merkez hanesinde daima 5 bulunmalıdır. Yani bir üçlü sihirli kare muhakkak \(\begin{smallmatrix}\_ & \_ & \_\\\_ & 5 & \_\\\_ & \_ & \_\end{smallmatrix}\) formunda olacaktır. Sol üst köşe farklı üç eleman üzerinde bulunmaktadır. Buraya yazılacak sayı listede en az üç seçenekte yer almalıdır. Bunu sağlayan dört sayı vardır: 2, 4, 6 ve 8. Şimdi, sol üst köşeye bu sayıları teker teker deneyerek yazalım. Önce 2… Bu durumda kare \(\begin{smallmatrix}2 & \_ & \_\\\_ & 5 & \_\\\_ & \_ & 8\end{smallmatrix}\) şeklinde olacaktır. Birinci sıra için ya \(\begin{smallmatrix}(2 & 4 & 9)\end{smallmatrix}\) ya da \(\begin{smallmatrix}(2 & 6 & 7)\end{smallmatrix}\) tercihini yapabiliriz. \(\begin{smallmatrix}(2 & 4 & 9)\end{smallmatrix}\)’u seçersek \(\begin{smallmatrix}2 & 9 & 4\\\_ & 5 & \_\\\_ & \_ & 8\end{smallmatrix}\) elde edilir. Satır, sütun toplamları 15 olacağından diğer haneler de tek türlü doldurulabilir. Neticede \(\begin{smallmatrix}2 & 9 & 4\\7 & 5 & 3\\6 & 1 & 8\end{smallmatrix}\) karesi ortaya çıkar. Birinci satır için \(\begin{smallmatrix}(2 & 6 & 7)\end{smallmatrix}\) tercihini yapsaydık elde edeceğimiz kare \(\begin{smallmatrix}2 & 7 & 6\\9 & 5 & 1\\4 & 3 & 6\end{smallmatrix}\) olacaktı. Sol üst köşeye 2 yazarak iki farklı kare elde ediyoruz. Aynı şekilde 4, 6 ve 8 için de ikişer kare bulunacak ve ortaya toplam sekiz tane 3’lü sihirli kare çıkacaktır. Bu tahlille göstermiş olduk ki, 3’lü sihirli karelerin sayısı tam sekizdir.
Lo-shu‘dan diğer kareleri elde ederken iki işlem kullandık: lo-shu‘yu merkezi etrafında döndürme ve aynada yansıtma… Bu işlemlere kısaca dönme ve yansıma adları verilir. Birbirinden dönme ve yansıma ile elde edilebilen sihirli karelere aynı kare gözü ile bakılır. Bu kabule göre, yukarıda bulduğumuz bütün 3’lü sihirli kareler lo-shu ile aynıdır. Bir başka deyişle, (dönme ve yansımalar sayılmazsa) yalnız bir tane 3’lü sihirli kare vardır. Sihirli karelerin dereceleri büyüdükçe sayalarının da artacağı kolaylıkla tahmin edilebilir. Bütün 3’lü sihirli kareler birbirlerine dönme ve yansıma ile dönüştürülebilirken, daha büyük derecelerde bu tür dönüşümlerle birbirlerinden elde edilemeyecek sihirli kareler de ortaya çıkmaya başlar. Örneğin aşağıdaki 5’li sihirli kareler birbirlerine dönme ve yansıma ile dönüştürülemezler.
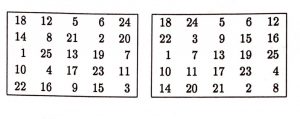
Kimi zaman sihirli kareler hane sayılarına göre, tek ve çift olarak tasnif edilirler. Bir kenardaki hane sayısı tek ise kareye tek sihirli kare; çift ise çift sihirli kare denir.
Bir \(n\)’li sihirli karenin iki satırının yerleri değiştirilirse satır ve sütun toplamları değişmeyecek fakat, köşegen toplamları bozulacaktır. Yani iki satırın yerini değiştirmek sihir koruyan bir dönüşüm değildir. Fakat iki satırın, diyelim ki, \(i\) ve \(j\) numaralı satırların yerini değiştirdikten sonra bir de \(i\) ve \(j\) numaralı sütunların yerini değiştirirsek birinci (sol-üst köşeden sağ-alt köşeye olan) köşegen üzerindeki toplam yine karenin sabitine eşit olur. İkinci köşegen toplamını da garanti edebilmek için yeter şart, yer değiştiren satır ve sütunların merkeze göre simetrik olmalarıdır. Yani \(j = n + 1 – i\) olmalıdır. Demek ki, bir sihirli karede önce \(i\) ve \(n + 1 – i\) numaralı satırlar, arkasından da aynı numaralı sütunlar yer değiştirirse yeni bir sihirli kare elde edilir.
‘Sihir-bozmaz’ bir başka dönüşüm de, kareyi bloklara ayırıp bu blokların yerlerinin değiştirilmesine dayanır. Bu dönüşümü tek ve çift kareler için ayrı ayrı tanımlıyoruz. Çift sihirli kareyi dikey ve yatay simetri eksenleri ile dört eşit parçaya bölerek elde edilen blokların yerlerini çarpraz olarak değiştirmek karenin sihirini bozmayacaktır. Bu dönüşümü bir şekille açıklarsak:
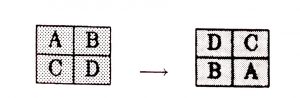
Aşağıda da bu dönüşümün bir 4’lü sihirli kareye uygulanması gösterilmiştir…

Tek sihirli kareler için ise, bloklara ayırma ve blokların yerini değiştirme işlemi aşağıdaki şekille izah edilmiştir.

Bir 5’li sihirli kare üzerinde bu dönüşümün etkisi şöyle olur:
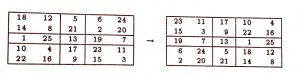
Bir \(n\)’li sihirli karenin her hanesindeki sayıyı \(n^2 + 1\)’den çıkararak elde edilen kare yine bir sihirli kare olur. Yukarıda son bulduğumuz 5’li sihirli karenin sayılarını 26’dan çıkararak oluşturulan

karesi de bir sihirli karedir.
Elimizdeki bir sihirli kareden sihir bozmaz dönüşümlerle birçok yeni sihirli kare elde edilebileceğini gördük. Hemen şunu not edelim ki, verilen bir kareyle işe başlayıp, bu kareye yukarıda tanımlanan ‘sihir-bozmaz’ dönüşümleri defalarca uygulayarak sihirli karelerin tamamını elde etmek mümkün değildir. Bildiğimiz işlemlerle birbirine çevrilemeyecek sihirli kareler bulunabilir. Verilen bir dereceden kaç tane sihirli kare olduğunu cevaplamak kolay bir iş değildir ve bir kaç hal dışında henüz bu soru cevaplandırılamamıştır.
Bir sihirli kareden yeni sihirli kareler elde edilebileceğini biliyoruz. O halde mesele, bir tane olsun bir sihirli kare yazabilmektir. Bu da konunun enteresan ve üzerinde epeyce çalışılmış bir problemidir. İstenen derecede bir sihirli kareyi hemen yazmak pek o kadar kolay olmayabilir. Yazının devamım okumadan, örneğin bir 6’lı sihirli kare yazmaya çalışmak problemin yapısı hakkında fikir verecektir. Verilen herhangi bir sayıya karşı gelen bir sihirli kare yazacak bir algoritma vermek konuyla ilgilenenlerin her zaman üzerinde durdukları bir mesele olmuştur. Çok uğraşılmasına rağmen bu mesele ancak kısmen cevaplandırılabilmiştir. Şöyle ki, eğer verilen sayı tek ise sihirli kareyi yazmak kolaydır. Bunu yapabilen çok basit algoritmalar geliştirilmiştir. Öte yandan, sayı çift olduğu takdirde uygulanabilecek basit bir yol mevcut değildir. Gerçi, her çift sayıya karşı bir sihirli kare yazabilmek mümkün olmaktadır. Ancak bunu veren algoritmalar, tek sayılar için verilenlerden oldukça karmaşıktır ve bunları basitleştirmek bugüne kadar mümkün olamamıştır. Burada tek kareler için birbirine çok benzeyen iki metod verilecektir. İlk metod Bachet de Méziriac tarafından geliştirilmiştir. Bu metodu kullanarak bir 7’li sihirli kare oluşturacağız. Uygulanan metod, herhangi dereceden tek sihirli kare yazmak için kullanılabilir.
İşe, her kenarında 7 hane bulunan boş bir karenin merkez hanesinin tam altındaki haneye 1 yazarak başlıyoruz. 1’in sağ-alt çarprazına 2 yazıyoruz. Bundan sonra 3, 4, 5, 6, 7 sayılarını bir önceki sayının sağ-alt çarprazına yerleştirmek sureti ile devam ediyoruz. 3 yazdığımız zaman karenin alt sınırına gelmiş olduğumuzdan, 4 yazacak bir sağ-alt çarpraz olmayacaktır. Bu durumda karenin son satırından sonra sanki ilk satırının devam ettiğini kabul edip, 3’ün sağ-alt çarprazı olarak, ilk satırın son hanesine 4 yazacağız. Benzer şekilde, 5 yazmak için de, 4’ün sağ-alt çarprazı olarak ilk satırın ikinci hanesini kullanacağız. 6 ve 7 sayılarını yazarken bir problem çıkmayacaktır… Şimdi elimizde şöyle bir kare oldu
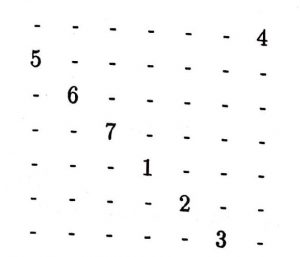
Bundan sonra 8 sayısını 7’nin 2 hane altına yazıp 9, 10, 11, 12, 13, 14 sayılarını da sıra ile ve hep bir öncekinin sağ-alt çarprazına gelmek sureti ile yazacağız. Karemiz şu şekli aldı:

14’ün iki hane altına 15 yazıp benzer şekilde devam edilerek bütün kare doldurulursa bir 7’li sihirli kare elde edilir:
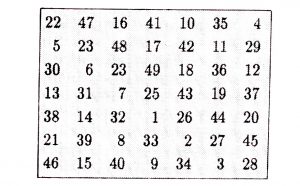
Burada kullandığımız algoritma her dereceden tek sihirli kare için kolayca genelleştirilebilir.
Tek sihirli kareler için, Bachet de Méziriac metoduna çok benzeyen bir metod da De la Loubère tarafından verilmiştir. Bu metodla karenin kuruluşu, iki ayrıntı dışında aynıdır… Sayıları yazmaya birinci satırın tam ortasındaki haneden başlıyor ve sağ-üst çarpraza doğru devam ederek diğer sayıları yerleştiriyoruz. Bir çarpraz dolduğu zaman da, kaldığımız yerden iki hane yerine yalnız bir hane iniyoruz. Aşağıdaki 7’li sihirli kare De la Loubere metodu ile yazılmıştır:
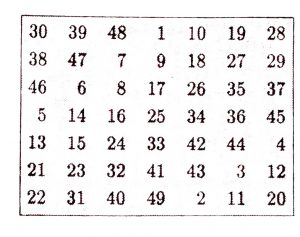
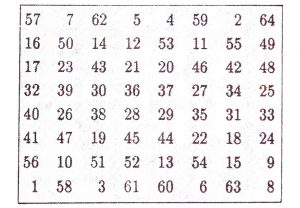
Karmaşık yapılarından dolayı, çift sihirli kareler için geliştirilen metodları bir başka sayıya bırakarak burada sadece iki örnek veriyoruz. Aşağıda verilen, biri 6’lı; diğeri 8’li iki sihirli kare, Devedec‘e ait metodla yazılmıştır.

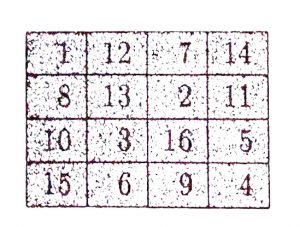
Son olarak çok fazla sihirli bir 4’lü kare veriyoruz. 4’lü bir sihirli karede, sabit toplam 34’dür. Bu kareyi inceledikçe hiç beklenmedik bir çok özelliğe sahip olduğu görülecektir. Bu karede satır, sütun ve köşegenlerden başka hangi hanelerin toplamının da 34 olduğu araştırılarak karenin sihiri hakkında bilgi edinmeye başlanılabilir.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

