Yazar: Hüseyin Demir
Bu yazımızda, pek çok çizim probleminin çözümünde ve bazı teoremlerin ispatında başarılı uygulamaları olan ilginç bazı geometrik dönüşümleri tanıtmak ve incelemek istiyoruz.
1. Tanım ve Özellikler
Uzaklıkları koruyan, noktalardan noktalara bir dönüşüme izometri deniliyor. Bu dönüşümleri $f, g$ harfleriyle göstereceğiz.
Bir $P$ noktası bir $f$ izometrisi ile bir $P’$ noktasına dönüştürülürse, $$f \colon P \to P’ \text{ ya da } f(P) = P’$$ yazılır ve $P’$ ye $P$ nin $f$ altındaki görüntüsü denir. Eğer ayrıca $f(Q) = Q’$ ise $f$ nin uzaklıkları koruması \begin{equation} |P’ Q’| = |P Q| \end{equation} anlamına gelir. Daha açık söyleyecek olursak, iki nokta arasındaki uzaklık, tanım gereği görüntüleri arasındaki uzaklığa eşittir.
Teorem: Bir izometri, bir doğru parçasını buna eş olan bir doğru parçasına dönüştürür.
Gerçekten, $f$ bir izometri, $[AB]$ bir doğru parçası ve $P \in [AB]$ olsun. O zaman $|AP| + |PB| = |AB|$ olur. $A, P, B$ noktalarının görüntüleri sırasıyla $A’, P’, B’$ ise (1) den $|A’P’| + |P’B’| = |A’B’|$ olup $P’ \in [A’B’]$ olduğunu gösterir ve ayrıca $|A’B’| = |AB|$ yi verir.
Bu teoremden hemen şu sonuç çıkar:
Sonuç: Bir $f$ izometrisi
(a) bir doğruyu bir doğruya
(b) bir ışını bir ışına
(c) bir üçgeni buna eş olan bir üçgene
(d) bir açıyı buna eş olan bir açıya
(e) bir çemberi buna eş olan bir çembere dönüştürür.
İlk dört şık, teoremin doğrudan sonuçları olup son şık şöyle gösterilir: Çemberin merkezi $A$, üzerindeki değişken bir nokta $P$ ve bunların görüntüleri $A’, P’$ ise $|A’P’| = |AP|$ sabit olup $P’$ nün geometrik yeri, $A’$ merkez olmak üzere $|A’P’| = |AP|$ yarıçaplı bir çemberdir.
Etkisiz ve Etkili İzometriler
Evrensel $U$ kümesinin (düzlemin ya da uzayın) her $P$ noktasını aynı $P$ noktasına dönüştüren izometriye etkisiz izometri der ve bu izometriyi $e$ harfiyle gösteririz. $$e(P) = P,~\forall P \in U.$$
$e$ den farklı izometrilere de etkili izometri deriz. Böyle bir izometri altında bazı noktalar başka noktalara dönüşür.
Değişmez Şekiller
Bir izometri altında kendisine dönüşen bir şekle izometrinin değişmez şekil‘i denir. Örneğin etkisiz $e$ izometrisi altında, her şekil değişmez bir şekildir. Başka örnekleri. § $2$’de göreceğiz.
İzometrilerin Tersi
Bir $f$ izometrisi altında $f(P) = P’,~\forall P \in U$ olduğunda bir $g$ izometrisi için $g(P’) = P$ ise $g$ ye $f$ nin tersi denir ve $g$ izometrisi $f^{-1}$ olarak yazılır. Buna göre $$f(P) = P’ \iff f^{-1}(P’) = P,~\forall P \in U$$ olur.
2. Düzlemde İzometriler
Düzlemde dört tür izometri yer almaktadır. Bunlar da öteleme, dönme, simetri ve yansıma diyeceğimiz izometrilerdir. Uzaydaki izometrileri konumuzun dışında bırakıyoruz.
Öteleme
Düzlemde $\vec{u} = \vec{AA’}$ gibi bir vektör verildiğinde, bir $P$ noktasını $$\vec{PP’} = \vec{AA’}$$ vektörel eşitliği ile tanımlı $P’$ noktasına dönüştüren dönüşüme öteleme ve $\vec{u}$ vektörüne öteleme vektörü deriz. Her vektör bir öteleme tanımlar.

Buna göre $$\vec{u}(P) = P’$$ yazarız. Ayrıca $$\vec{u}(Q) = Q’$$ ise $PP’QQ’$ bir paralelkenar (ya da yoz paralelkenar) olup $|P’Q’| = |PQ|$ çıkar. Bu da ötelemelerin birer izometri olduğunu gösterir.
$\vec{u} = 0$ ötelemesinin etkisiz, ötekilerin ise etkili olacağı açıktır.
Etkili bir $\vec{u}$ ötelemesi altında değişmez şekiller ancak $\vec{u}$ yu taşıyan doğru ile $\vec{u}$ ya paralel olan doğrulardır.
$\vec{u}$ ötelemesinin tersi ise $-\vec{u}$ ötelemesidir.
Dönme
$O$ sabit bir nokta ve $\alpha \in \mathbb{R}$ ise düzlemin her $P$ noktasını
(i) $|OP’| = |OP|$
(ii) $\sphericalangle POP’ = \alpha$
olarak tanımlı $P’$ noktasına dönüştüren dönüşüme dönme, $O$ noktasına dönme merkezi, $\alpha$ ya da dönme açısı denir.
Bu dönmeyi $(O, \alpha)$ simgesiyle gösterir ve $$(O, \alpha)(P) = P’$$ yazarız.
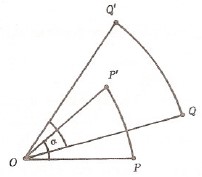
Ayrıca $(O, \alpha)(Q) = Q’$ ise $\triangle POQ \cong \triangle P’OQ’$ eşliği nedeniyle $|P’Q’| = |PQ|$ olup dönmeler birer izometridir.
$(O, \alpha)^{-1} = (O, -\alpha)$ olacağı açıktır.
$k \in \mathbb{R}$ ise $(O, 2k\pi)$ ve özellikle $(O, 0)$ dönmesi etkisizdir.
Etkili bir $(O, \alpha)$ dönmesinin değişmez şekilleri ancak $O$ merkezli çemberlerdir. ($a \neq \pi$)
Şimdi dönme ile ilgili şu çizim problemini ele alalım:
Problem: $[AB], [A’B’]$ gibi birbirine eş ve paralel olmayan iki doğru parçası verildiğinde, $[AB]$ yi $[A’B’]$ ye gönderen $(O, \theta)$ dönmesini belirlemek.
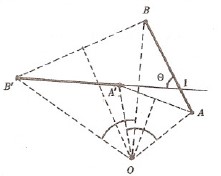
$A$ ve $B$ noktaları dönme ile karşılıklı olarak $A’$ ve $B’$ ye gönderildiğinden $O$ dönme merkezi $[AA’]$ ve $[BB’]$ doğru parçalarının orta dikmeleri üzerinde bulunmalıdır. Öyle ise bunların arakesiti $O$ merkezini verir.
Dönmenin gereği olarak, dönmenin $\theta$ açısı da $$\theta = \sphericalangle AOA’ = \sphericalangle BOB’$$ eşitlikleri ile belirlidir.
Öte yandan $AB \cap A’B’ = I$ ise $[AB] \to [A’B’]$ nedeniyle $$\theta = \sphericalangle (AB, A’B’) = \sphericalangle BIB’$$ elde edilir. Bu ise $AIA’O$ ve $B’BIO$ dörtgenlerinin birer kirişler dörtgeni olduğunu gösterir. Bu da $O$ merkezi için şu çizimi verir: $O$ merkezi $(AIA’), (BIB’)$ çemberlerinin öteki arakesit noktasıdır.
Simetri (Noktaya Göre Simetri)
$O$ gibi sabit bir nokta verildiğinde, bir $P$ noktasını $O$ ya göre $P’$ simetriğine gönderen dönüşüme simetri denir.
Bu simetriyi $O$ harfiyle gösterip $O(P) = P’$ yazarız.
$O$ simetrisi $(O, \pi)$ dönmesi olup simetriler birer izometridir.
$$O(P) = P’ \iff O(P’) = P$$ olup $O^{-1} = O$ elde edilir.
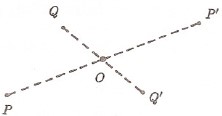
Soru: $O$ simetrisi hangi doğru ve çemberleri değişmez bırakır?
Yansıma (Doğruya Göre Simetri)
$a$ gibi sabit bir doğru verildiğinde her $P$ noktasını $a$ ya göre $P’$ simetriğine gönderen dönüşüme yansıma denir.
Bu yansımayı $a$ harfiyle gösterip yansıma ekseni der ve $$a(P) = P’$$ yazarız.
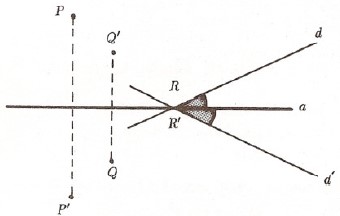
$a^{-1}$ ters yansımasının yine $a$ yansıması olduğunu görüyor ve yansımaların etkili olduklarını anlıyoruz.
Soru: Yansıma hangi nokta, doğru ve çemberleri değişmez bırakır?
3. Uygulamalar
Şimdi bazı çizim problemlerinin çözümünde ve bazı teoremlerin ispatında, öğrenmiş olduğumuz öteleme, dönme, simetri ve yansıma izometrilerinin herbirinin uygulamalarını ayrı ayrı ele alacağız.
Bu işi yapmayı denerken hangi izometrinin kullanılacağını kestirmek sezgiye dayanan bir iştir. Bununla birlikte, bazı sade problemlerin çözümünde her zaman geçerli olmamakla birlikte şu kuralı uygularız:
Kural 1: Eğer bir problemde
a) doğrultusu ve uzunluğu verilmiş bir doğru parçası söz konusu olursa, öteleme
b) tepesi ve tepe açısı bilinen ikizkenar bir üçgen söz konusu olursa, dönme
c) orta noktası verilen doğru parçası söz konusu olduğunda, simetri
d) açıortayı ile birlikte bir açı söz konusu ise, yansıma
kullanılabilir.
Uygulama 1. Aşağıda düz bir $d$ yolu ile ayrılmış $A$ ve $B$ gibi iki ev (nokta) verilmiştir. $A$ dan çıkan bir kişi yola varıp uzunluğu belli $[EF]$ yolunu yürüdükten sonra $B$ ye varacaktır. En kısa yolu bulunuz.
Çözümü okumadan düşünün. Kuralın hangi şıkkı geçerli?
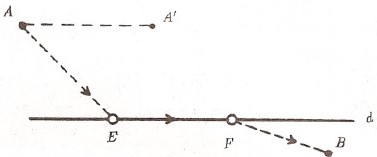
Kural 1a geçerli.
$A$ yı $\vec{EF}$ ötelemesiyle $A’$ ye götürdüğümüzde yolumuz $[AEFB]$ yerine $[AA’FB]$ olur. Burada $[AA’]$ sabit olup $[A’FB]$ yolu en kısa olmalıdır. O halde $F = A’B \cap d$ olarak belirlenir. Bu da $E$ yi verir.
Uygulama 2. Şekilde, $b$ ve $c$ gibi iki doğru ve bir $A$ noktası verilmiştir.
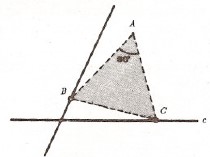
$B \in b$, $C \in c$ olmak üzere eşkenar $ABC$ üçgenini çizmek.
Kural 1b geçerli.
$(A, 60^{\circ})$ dönmesini $\{b, B\}$ şekline uyguladığımızda $\{b’, B’\}$ şekli elde edilir. $B’ = C$ olması gerekir ve $C = b’ \cap c$ olarak bulunur. Bu da $B$ yi verir.
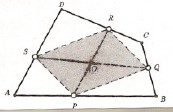
Uygulama 3. Genel bir $ABCD$ dörtgeni içine, $O$ merkezi verilen $PQRS$ paralelkenarını çizmek.
Kural 1c geçerli.
$O$ noktası $[PR]$ nin ortası olup $\{CD, R\}$ şekline $O$ simetrisi uygulandığında $\{C’D’, R’\}$ görüntüsü elde edilir. Burada $R’ = P = C’D’ \cap AB$ olarak belirlenir.
Benzer olarak $Q$ elde edilir.
Uygulama 4. $ABCD\colon a, b, c, d \ \sphericalangle BAC = \sphericalangle CAD$.
Burada, kenar uzunlukları verilen ve bir köşegeni bir açısının açıortayı olan bir dörtgenin çizimi söz konusu.
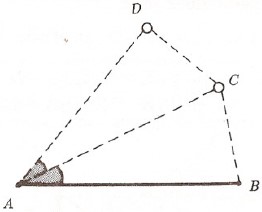
Kural 1d geçerli.
$DAC$ üçgenine $AC$ yansıması uygulanırsa $D$ nin $D’$ görüntüsü $AB$ üzerinde bulunur ve $CD’B$ üçgeni $a-d, b, c$ kenarlarıyla belirlidir. $D’$ nün $AC$ ye göre simetriği de $D$ yi verir.
Şimdi Kural 1’in geçerli olmadığı şu uygulamayı ele alalım.
Uygulama 5. Bir $ABC$ üçgeni ve bir $d$ doğrusu verildiğinde $[AC]$, $[AB]$ üzerinde
(i) $EF // d$
(ii) |BF| = 2 |CE|
olmak üzere $E$ ve $F$ noktalarını çizmek.

Kural 1’in geçerli olmaması halinde, şu kuralı uygularız:
Kural 2: Uygun bir izometri ile şeklin bazı elemanları başka elemanların yanına taşınır. Elde edilen yeni şekil incelenip çözüme götürecek bazı bağıntılar elde edilir.
Bu kuralı uygulamak görüş ve sezgiye dayanır.
Şimdi Kural 2’yi uygulayarak Uygulama 5’in çözümünü elde etmeğe çalışalım.
$[BF]$ yi bir öteleme ile $[B’E]$ doğru parçasına gönderebiliriz. Ortaya $EB’C$ gibi $E$ açısı sabit ve iki kenar uzunluğu orantılı bir üçgen çıkar. $EF$ doğrusu $d$ ye paralel olarak değiştiğinde $B’CE$ açısı sabit kalıp $B’$ nün geometri yeri $C$ den geçen bir $e$ doğrusu olur. Probleme cevap verecek $B’$ noktası, $e$ yi $B$ den $d$ ye paralel olan doğru ile kesiştirmekle bulunur. $B’$ bulununca önce $E$, sonra $F$ elde edilir.
Uygulama 6. Teorem: Bir çember içine bir $ABC$ eşkenar üçgeni çizildiğinde $A$ karşısındaki $\widehat{BC}$ yayı üzerinde alınan bir $P$ noktasının $B$ ve $C$ den uzaklıkları toplamı, $A$ dan uzaklığına eşittir.
Kural 1 işe yaramıyor. Kural 2 ile $CBP$ üçgenine $(C, -60^{\circ})$ dönmesini uygulayıp $CAP’$ üçgenini elde edelim. Böylece $[PB]$ doğru parçası $[PA]$ üzerine taşınmış olur. (işaretli eş açılardan)
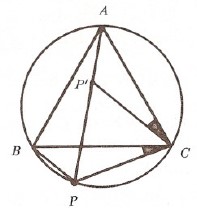
Geriye $|PP’| = |PC|$ olduğunu göstermek kalır. Bu da $P’PC$ nin eşkenar olması sonucudur.
Uygulama 7. Fermat Problemi: Dar açılı bir $ABC$ üçgeninin içinde, köşelerden uzaklıkları toplamı en küçük olan $F$ noktasını bulmak.
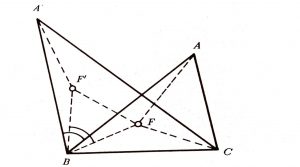
$|PA| + |PBl + |PC|$ toplamını kesik bir çizginin uzunluğuna çevirmek üzere $ABF$ üçgenine $(B, 60^{\circ})$ dönmesini uygulayıp $A’BF’$ görüntüsünü elde edelim. $BFF’$ nün eşkenar üçgen olması nedeniyle kırık çizgimiz $[A’F’FC]$ olur. Bunun ise en kısa uzunluğu $|A’C|$ dir.
Öyle ise $F$ noktası $A’C$ üzerinde bulunmalıdır. Bu da $$\sphericalangle BFC = 180^{\circ} – \sphericalangle BFF’ = 180^{\circ} – 60^{\circ} = 120^{\circ}$$ verir. O halde $F$ noktası $[BC]$ yi $120^{\circ}$ altında görür. Benzer olarak öteki iki kenarı da $120^{\circ}$ altında görür. Bu noktayı belirlemek için şu çizimi veriyoruz:
1. $ABC$ nin kenarları üzerine dıştan $XBC, YCA, ZAB$ eşkenar üçgenleri çizilir.
2. $AX, BY, CZ$ doğruları $F$ de kesişir.
Uygulama 8. Teorem. Dar açılı bir üçgende iç üçgenlerden çevresi en küçük olanı ortik üçgendir.
Bir $ABC$ üçgeninin ortik üçgeni, köşeleri, yüksekliklerin kenarlar üzerindeki ayakları olan üçgendir.
Dar açılı bir $ABC$ nin $DEF$ ortik üçgeninin bilinen bazı özellikleri şunlardır:
1. $ABC$ nin yükseklikleri $DEF$ nin iç açıortaylarıdır.
2. $ABC$ nin kenarları $DEF$ nin diş açıortaylarıdır.
3. $ABC \sim AEF \sim BFD \sim CDE,$
4. $\sphericalangle BDF = \sphericalangle CDE = \sphericalangle BAC.$
İspat: Dar açılı üçgen $ABC$ ve bir iç üçgeni $DEF$ olsun. $D$ yi sabit bırakıp en küçük çevre veren $E$ ve $F$ noktasını bulalım.
Uygun bir izometri kullanarak çevreyi kırık bir çizgiye dönüştürelim. $D$ nin $CA$ ve $BA$ yansımalarına göre $D2$, $D3$ simetrilerini aldığımızda kırık çizgimiz $[D_2EFD_3]$ olur.
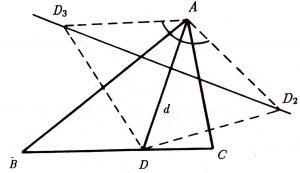
$D_2$, $D_3$ sabit olup kırık çizginin en kısa uzunluğu $|D_2D_3|$ olur. $|AD| = d$ ise $|AD_2| = |AD_3| = d$ ve $\sphericalangle D_2AD_3 = 2A$ olup $AD_2D_3$ ikizkenar üçgendir ve $$|D_2D_3| = 2 d \sin A$$ bulunur. Burada $\sin A$ sabit olup en küçük çevrelerin $d = |AD_0| = h_a$ olmalıdır, yani $[AD]$, $ABC$ nin $[AD_0]$ yüksekliği olmalıdır.
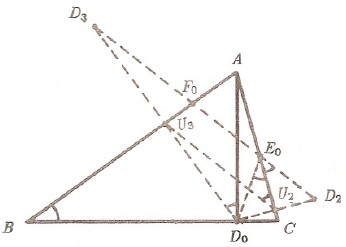
Bu durumda $D_2D_3$ ün $AC$ ve $AB$ yi kestikleri $E_0$ ve $F_0$ noktalarının öteki yüksekliklerin ayakları olduğunu gösterelim.
Bunun için $\sphericalangle CD_0E_0 = A$ ya da $\sphericalangle D_0E_0C = B$ olduğunu göstermek yeter.
Gerçekten $[D_0D_2]$, $[D_0D_3]$ ün ortaları $U_2$, $U_3$ ise \begin{align*} \sphericalangle CE_0D_0 &= \sphericalangle CE_0B_2 = \sphericalangle CE_0B_2 = \sphericalangle F_0E_0A\\&= \sphericalangle U_3U_2E_0 = \sphericalangle U_3D_0A = \sphericalangle D_0BU_3 = B \end{align*}
Aşağıdaki iki uygulamayı kendiniz çözünüz.
Uygulama 9. Eşitkenar bir $ABC$ üçgeninin içine, $D$ tepesi $[BC]$ üzerinde $[EF]$ tabanı $BC$ ye paralel olan $DEF$ üçgeni çiziniz.
Uygulama 10. Bir $d$ doğrusu ile bunun aynı tarafında iki çember verildiğinde $d$ ye paralel olup çemberlerden eş kirişler ayıran bir doğru çiziniz.
$\rule{130pt}{4pt}$
Kaynak
PETERSEN, J., Geometri Problemleri için Metotlar ve Teoriler (Çeviren: F. Gürsan), Şirketi Mürettibiye Basımevi, İst., 1943.
$1! = 1$ $2! = 2$ $1! + 4! + 5! = 145$ $4! + 0! + 5! + 8! + 5! = 40585$ Bu özellikte başka sayılar bulabilir misiniz?
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

