Yazar: Nurettin Çalışkan
Kenarlarının uzunluğu $a$ birim olan bir $ABC$ eşkenar üçgeni alalım. $D_1, E_1, F_1$, sırasıyla $AB, BC$ ve $AC$ kenarlarının orta noktaları olsun. $D_1, E_1$ ve $E_1, F_1$ noktalarını birleştirerek elde edilen $BD_1E_1$ ve $E_1 F_1C$ üçgenleri, kenar uzunlukları $a/2$ olan eşkenar üçgenlerdir, dolayısıyla
$$|BD_1| + |D_1E_1| + |E_1F_1| + |F_1C| = 4 \frac{a}{2} = 2a$$ olur. Aynı şekilde $D_2, E_2, G_1, H_1, E_3$ ve $F_2$ noktaları, sırasıyla $BD_1, BE_1 , D_1E_1, E_1F_1, E_1C$ ve $F_1C$ doğrularının orta noktaları olsun. Elde ettiğimiz $BD_2E_2, E_2G_1E_1, E_1H_1E_3$ ve $E_3F_2C$ üçgenleri kenar uzunlukları $a/4$ olan eşkenar üçgenlerdir ve $$|BD_2| + |D_2E_2| + |E_2G_1| + |G_1E_1| + |E_1H_1| + |H_1E_3| + |E_3F_2| + |F_2C| = 8\frac{a}{2} = 2a$$ olur.
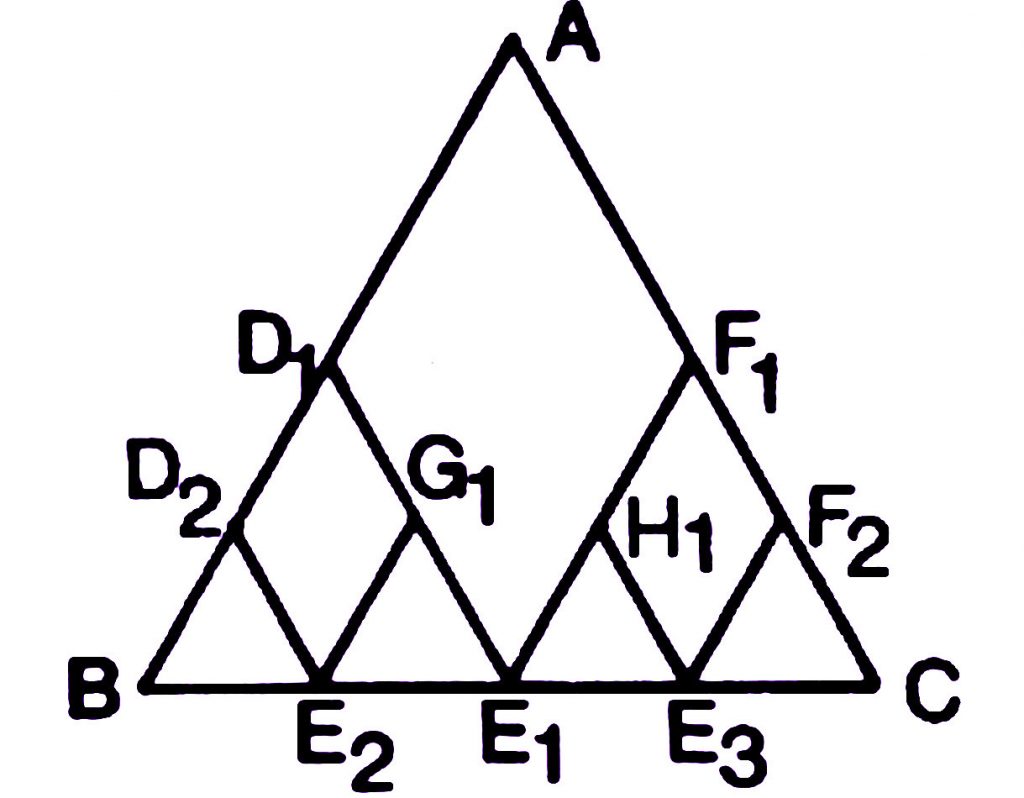
Böylece devam edecek olursak, her defasında, $BC$ kenarına en yakın olarak elde edilecek kırık çizginin uzunluğu değişmeyecek, daima $2a$ olarak kalacaktır. Bu kırık çizginin $BC$ kenarına istenildiği kadar yaklaştırılabileceği düşünülürse, $$|BC| = 2a = |AC| + |AB|$$ sonucuna varılır.
Nerede hata yapılmıştır?

