Doğal Dil İşleme Modellerinin Matematiksel Temelleri

Yazar: Berkay Anahtarcı, berkay.anahtarci@ozyegin.edu.tr ve Zehra Kesemen, zehra.kesemen@ozu.edu.tr

Yıl: 2024-1

Sayı: 119

Giriş

Yapay zekâ, bilgisayar sistemlerine insan benzeri zekâ ve öğrenme yetenekleri kazandırmayı amaçlayan bir teknoloji dalıdır. Doğal Dil İşleme (Natural Language Processing: NLP) ise yapay zekânın temel bileşenlerinden biri olarak öne çıkar. NLP aracılığıyla, bilgisayarlar yazılı metinleri, konuşma ve diğer dil formlarını işleyerek insanlarla doğal bir diyalog kurabilir. Apple’ın Siri’si ve Google Asistan gibi sanal yardımcılar, Google Translate gibi çeviri uygulamaları ve müşteri hizmetlerindeki sohbet robotları, NLP’nin günlük yaşamda karşılaştığımız örneklerindendir. Ancak NLP’nin uygulama alanları bu kadarla sınırlı değildir; biyoinformatikte gen ifadesi ve genetik dizilim analizi, tıbbi literatürden veri madenciliği sonucu bulgu çıkarımı, finans sektöründe piyasa trendleri tahmini ve risk yönetimi gibi çeşitli alanlarda NLP teknolojileri etkin bir şekilde kullanılmaktadır.

NLP alanındaki evrim, 1950’lerden 1980’lere kadar olan ilk dönemlerinde, dil karmaşıklığı ve sınırlı işlem gücü nedeniyle dilbilgisel kurallara dayalı sistemlerin kullanımıyla şekillenmiştir. 1990’lar ve 2000’lerde istatistiksel yaklaşımların ön plana çıkmasıyla birlikte, dil anlama görevlerinde daha iyi performans elde edilmiştir. Ancak bu dönemde semantik¹ kısıtlamaların üstesinden gelmek hâlâ bir sorundur. 2010’ların başında, Thomas Mikolov’un öncülüğünde geliştirilen kelime gömme yöntemleri, semantik ilişkilerin anlaşılmasını sağlayarak NLP alanında büyük bir atılım yapmıştır.

Dil anlama, yapay zekâ alanında hem büyük bir meydan okuma hem de önemli bir fırsat olarak karşımıza çıkmaktadır. 2010’lardan bugüne, derin öğrenme (deep learning) ve üretici ön-eğitimli dönüştürücü (Generative Pre-training Transformer: GPT) gibi büyük dil modelleri (Large Language Models: LLM), dil anlama görevlerinde önemli başarılar elde etmiştir. Ne var ki dil tek başına yeterli değildir. İnsanlar, dilin yanı sıra görsel ve işitsel bilgilere de başvurarak anlam üretirler. Bu durum, son yıllarda transfer öğrenme (transfer learning) ve çok modlu (multimodal) modellerin geliştirilmesine yol açmıştır. Bu modeller, dil, görüntü ve ses gibi farklı veri türlerini birleştirerek dilin daha kapsamlı bir şekilde anlaşılmasını amaçlamaktadır.

NLP tarihi boyunca, metinleri matematiksel modellerle temsil etme çabaları öne çıkmıştır. Kelime sıklığı, gramatik yapı ve semantik ilişkiler gibi dilsel özelliklerin matematiksel analizleri, bu alandaki temel çalışmaları oluşturmuştur. Bu yazıda, NLP çalışmalarında önemli bir dönüm noktası olarak kabul edilen kelime gömme modellerinin matematiksel temellerine odaklanacağız.

Kelimelerin Sayısal Temsiliyeti

Bilgisayarların metin içindeki kelimeleri anlaması ve çeşitli analizler gerçekleştirebilmesi için kelimeler sayısal ifadelerle temsil edilmelidir. Bu sayede, dilin soyut yapısı matematiksel işlemlere tabi tutulabilir ve çeşitli görevler gerçekleştirilebilir. Genellikle, her kelime bir vektör veya matris olarak ifade edilir. Kelimeleri sayısal olarak ifade etmenin bazı yaygın yöntemleri arasında Standart Baz Vektörü Yöntemi, Kelime Çantası Modeli ve Kelime Gömme Modelleri bulunmaktadır.

Standart Baz Vektörü Yöntemi

Standart baz vektörü yöntemi (one-hot encoding), NLP alanında, kelimelerin anlamsal ve sözdizimsel ilişkilerini analiz etmek için kullanılan bir tekniktir. Her kelime, korpusta² sıralandığı konumda sadece bir tane $1$ ve geri kalan tüm elemanları $0$ içeren bir vektörle temsil edilir. Buna literatürde bir vektörün one-hot gösterimi denir ve bu sayede kelimelerin sayısal değerler içeren vektörlerle temsili elde edilmiş olur.

Korpusu Türkçe bir sözlük olarak belirleyelim ve $\mathcal{S}$ ile temsil edelim. Toplam kelime sayısını da $|\mathcal{S}| := d$ varsayalım. Her kelimeyi sırasıyla aşağıdaki gibi $d \times 1$ boyutunda kendine özgü ve benzersiz bir kelime vektörüyle ifade edebiliriz:

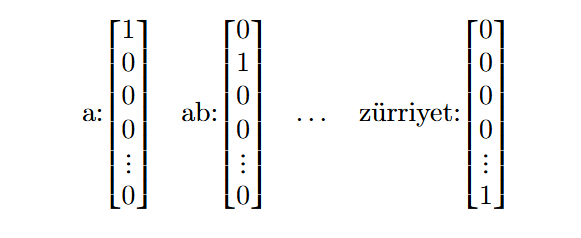
Bu yöntem basit ve anlaşılır olmasına rağmen, büyük veri kümelerinde boyut sorunlarına yol açabilir. Çünkü korpustaki her kelime için ayrı bir vektör oluşturmak, hem bellek hem de işlem açısından çok maliyetli olabilir.

Kelime Çantası Modeli

Kelime Çantası Modeli (Bag of Words: BoW), bir metnin içeriğini, metinde bulunan kelimelerin frekanslarına³ göre temsil eden bir yöntemdir. Bu yöntem, metni kelime kümesi olarak ele alıp kelimelerden bir korpus oluşturur. Sayısal temsiliyet için metinlerdeki kelimelerin cümlede görünme sayısı hesaplanır; bu sayı metnin vektöründe kelimenin bileşenine karşılık gelen değerdir.

Örneğin,

“Ali ata bak, bak Ali bak!”

cümlesini ele alalım. Noktalama işaretleri ve özel karakterler temizlendikten sonra kelimelerin frekans tablosunu oluşturabiliriz:

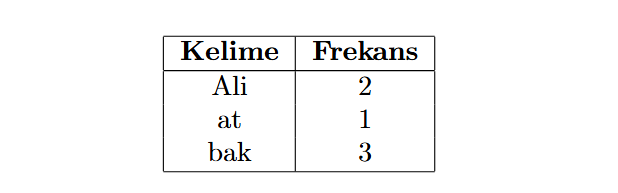
Diğer yandan “Ali ata bak, bak Ali bak!” cümlesinin kelimelerini $d \times 1$ boyutlu standart baz vektörleriyle aşağıdaki gibi ifade edebiliriz:⁴

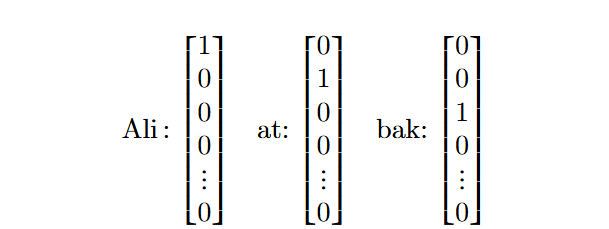
Frekans tablosunun da yardımıyla “Ali ata bak, bak Ali bak!” cümlesi aşağıdaki $d \times 1$ boyutlu vektör ile temsil edilir:

$$\begin{bmatrix} 2 & 1 & 3 & 0 &\cdots & 0\end{bmatrix}^\intercal.$$

Farklı cümlelerin temsil vektörleri yukarıdaki örnekteki gibi elde edildikten sonra bu cümlelerin birbirine olan benzerliği, onları temsil eden vektörler üzerinde uygulanan çeşitli metriklerle hesaplanır. Bu ölçümler için Öklid mesafesi, kosinüs benzerliği ya da Jaccard indeksi gibi farklı yöntemler tercih edilebilir.

Öte yandan, BoW modeli metindeki kelimelerin sırasını ve bağlamını dikkate almaz. Bu durum, metnin anlamını tam olarak yansıtamamasına neden olabilir. BoW modelinin kısıtlarını aşmak için Word2Vec (CBoW ve Skip-Gram), GloVe (Global Vectors) gibi daha gelişmiş yöntemler kullanılabilir. Bu yazıda, Word2Vec hakkında detaylı bir inceleme yapacağız.

Kelime Gömme Modelleri

Kelime gömme (word embedding) modelleri, kelimelerin anlamlarını ve aralarındaki ilişkileri de dikkate alır. Bu yöntem, kelimeleri vektörlere indirgeyerek vektör uzayı özelliklerini kullanmamıza olanak sağlar. Böylece, kelimelerin anlamsal benzerlikleri ve farklılıkları sayısal olarak ölçülebilir hale gelir.

Kelime gömme yöntemi, kelimeleri ve ifadeleri yüksek boyutlu bir uzayda noktalara eşler. Bu uzayda, anlamları benzer olan kelimeler birbirine yakın, anlamları farklı olan kelimelerse birbirinden uzak konumlanır. Bu sayede, kelimeler arasındaki anlamsal benzerliği ve uzaklığı hesaplayabilir, ayrıca kelimeler üzerinde çeşitli işlemler yapabiliriz.

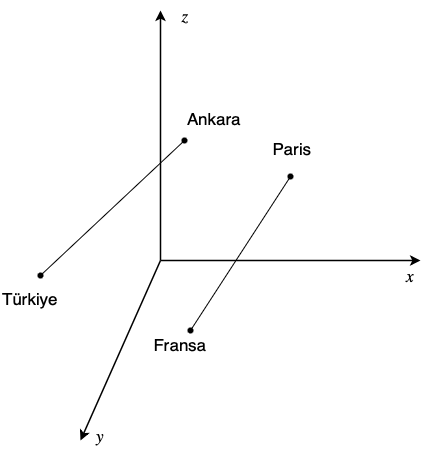
Görsel 2’de, Türkiye’nin başkenti Ankara’nın vektörü ile Fransa’nın başkenti Paris’in vektörü neredeyse paraleldir. Bu durum, bu iki çiftin benzer bir ülke-başkent ilişkisine sahip olduğunu gösterir:

$$\textit{v}_{\text{Paris}}- \textit{v}_{\text{Fransa}} \approx \textit{v}_{\text{Ankara}}- \textit{v}_{\text{Türkiye}}$$

ya da eşdeğer olarak,

$$\textit{v}_{\text{Paris}}- \textit{v}_{\text{Fransa}} + \textit{v}_{\text{Türkiye}} \approx \textit{v}_{\text{Ankara}}.$$

Tersten gidersek; Paris, Fransa ve Türkiye kelimelerinin gömme vektörleri yardımıyla Ankara kelimesini bulabiliriz. Tahmin etmeye çalıştığımız vektöre $\textit{a}$ diyelim ve kosinüs benzerliğini kullanalım:

$$\textit{a}= \underset{w \in \mathcal{S}}{\arg\max} \cos { \textit{v}_w, \textit{v}_{\text{Paris}}- \textit{v}_{\text{Fransa}} + \textit{v}_{\text{Türkiye}} }.$$

Başka bir şekilde ifade edersek, öyle bir $w\in \mathcal{S}$ kelimesi arıyoruz ki $ \textit{v}_w$ ve $\textit{v}_{\text{Paris}}- \textit{v}_{\text{Fransa}} + \textit{v}_{\text{Türkiye}}$ vektörlerinin arasındaki açının kosinüsü $1$’e en yakın olsun. Bu durum, söz konusu iki vektörün arasındaki açının neredeyse $0$ derece olmasına ve dolayısıyla gömme vektörlerinin paralel olmasına karşılık gelir.

Kelime gömme benzetmesi (analogy) olarak bilinen bu yöntem, kelimelerin anlamlarının bağlama göre değişebileceğini ve bazen de çelişkili olabileceğini göz önüne almaz. Bu nedenle, kelime gömme benzetmesi, her zaman doğru veya tutarlı sonuçlar vermeyebilir.

Word2Vec

BoW’a kıyasla daha gelişmiş sayılan Word2Vec kelime gömme modelleri, büyük metin veri kümeleri üzerinde eğitilen sinir ağları aracılığıyla oluşturulur. Bu ağlar, kelimelerin bağlamsal kullanımlarını analiz ederek her kelime için bir vektör oluşturur. Bu vektörler, kelimelerin anlamsal ilişkilerini ve benzerliklerini gösteren bir kelime uzayı meydana getirir. Yazımızda, Word2Vec’in iki modeli olan CBoW ve Skip-Gram’ı inceleyeceğiz.

Sürekli Kelime Çantası Modeli

Sürekli Kelime Çantası (Continuous Bag of Words: CBoW) modeli, sinir ağı tabanlı bir yaklaşımdır ve kelimelerin bağlamını öğrenir. Bu model, bağlam kelimelerini girdi olarak alır ve hedef kelimenin olasılık dağılımını çıktı olarak verir. Verili bir cümlede, tahmin etmeye çalıştığımız kelime merkez kelime olarak kabul edilir ve belirli bir pencere boyutu tanımlanır. Örneğin, pencere boyutu 3 olduğunda, merkez kelimenin hem sağındaki hem de solundaki üç kelime bağlam kelimelerini oluşturur. Detaylı bir CBoW örneğini yazımızın sonunda inceleyeceğiz.

Yukarıda bahsettiğimiz hedef kelimenin olasılık dağılımı modelin eğitim sürecinde gerçek hedef kelime ile tahmin edilen kelime arasındaki farkı azaltmak için kullanılır. Bu sayede, CBoW modeli, benzer bağlamda kullanılan kelimelerin gömme vektörlerinin birbirine yakın olmasını sağlar. Bu yöntem, doğal dil işleme görevlerinde kullanılan anlamsal ve sözdizimsel bilgileri etkili bir şekilde yakalar. Bu, dil modellemesi ve metin sınıflandırma gibi görevlerde önemli bir rol oynar.

Hesapları sadeleştirmek ve bir sonraki bölümde bahsedeceğimiz Skip-Gram modeliyle benzerlik kurmak adına pencere boyutunu 1 kabul edip yalnızca tek bir bağlam kelimesi $c$’ye sahip olduğumuzu varsayalım ve ondan sonra gelen kelime $w$’yu tahmin etmeye çalışalım.

Giriş katmanını (input layer) $d \times 1$ boyutlu standart baz vektörü

\begin{equation*} \textit{x}= \begin{bmatrix} x_1 & x_2 & \cdots & x_d \end{bmatrix}^\intercal \end{equation*}

ile temsil edelim; yani $x_k=1$ ve $k\neq k’$ için $x_{k’}=0$ olduğunu varsayalım. Burada $d$ korpusun boyutunu, $k$ ise bağlam kelimesinin indisini gösterir.

İlk hedefimiz, tüm korpustaki kelimelerin sayısına eşit olan $\textit{x}$ vektörünün boyutunu daha küçük bir boyuta indirgemektir. Bu daha küçük boyutlu temsil vektörünü $\textit{h}$ olarak adlandıralım ve bunu bir gizli katman (\textit{hidden layer}) olarak tanımlayalım. Bu geçişin sağlanması için $\textit{W}$ adını verdiğimiz bir ağırlık matrisi kullanacağız. Boyutlarıyla ifade edersek,

$$\textit{h}_{p\times 1}=\textit{W}^\intercal_{p\times d} \textit{x}_{d \times 1}$$ olur.

Burada $\textit{h}$ vektörü, $\textit{x}$ vektörünün sadece bir girdisi $1$ diğerleri $0$ olduğundan, aslında $\textit{W}^\intercal$ matrisinin $k$’inci sütunu (veya başka bir deyişle $\textit{W}$ matrisinin $k$’inci satırı) olacaktır. Bu temsil vektörü bağlam kelimesiyle ilişkili olduğundan, $\textit{h}=\textit{v}_c$ şeklinde yazacağız. Sonuç olarak $\textit{v}_c$ bağlam kelimesinin gömme vektörünü temsil eder.

Gösterim kolaylığı için, $\textit{W}$ matrisinin $i$’nci sütununu $\textit{W}_{\cdot i}$ ifadesiyle, $j$’inci satırınıysa $\textit{W}_{j \cdot}$ ile gösterelim. Böylece şu eşitliği yazabiliriz:

$$ \textit{h}=\textit{W}_{k\cdot}^\intercal =\textit{v}_c. $$

Bir sonraki aşamada, $\textit{h}$ vektörünü bir olasılık vektörüne dönüştürmeden önce, başka bir ağırlık matrisi olan $\textit{W}’$ yardımıyla adına $\textit{u}$ diyeceğimiz yeni bir vektör elde edeceğiz:

$$\textit{u}_{d \times 1}=\textit{W}’^\intercal_{d \times p} \textit{h}_{p \times 1}.$$

Bu durumda $\textit{u}$’nun $j$’inci bileşeni $u_j=\textit{W}’_{\cdot j} \ ^{\intercal} \textit{h}$ (veya bir başka deyişle $\textit{u}_j=\textit{W}’_{j \cdot} \textit{h}$) olur. Bu kez $w$ ile ilişkili olduğu için $\textit{W}’_{\cdot j}=\textit{v}_{w_j}$ yazalım. Dolayısıyla şu ifadeyi elde ederiz:

$$u_j=\textit{v}_{w_j}^\intercal \cdot \textit{v}_c.$$

Hedefimiz, çıktı katmanı olarak adlandırılan ve bir olasılık dağılımı vektörü olan $d \times 1$ boyutlu $\textit{y}$’yi elde etmektir. Bu vektör, korpustaki her bir kelimenin olasılık dağılımını temsil eder. $\textit{y}$ vektörünün her bir bileşenini hesaplamak için softmax fonksiyonu $\phi$ kullanılır. Softmax fonksiyonu, her bir öğenin değerini 0 ile 1 arasında bir aralığa dönüştürerek, olasılık dağılımı oluşturmaya uygun hale getirir. Dolayısıyla, $\textit{y}$ vektörünün $j.$ bileşeni, aşağıdaki formülle hesaplanır:

$$y_j= \phi(u_j)=\frac{\exp{(u_j)}}{\sum_{j’=1}^d \exp {(u_{j’})}}.$$

Sonuç olarak, $u_j$ ifadesini softmax fonksiyonuna girdi olarak koyarsak, aşağıdaki ifadeyi elde ederiz:

$$y_j= \frac{\exp{(\textit{v}_{w_j}^\intercal \cdot \textit{v}_c})}{\sum_{j’=1}^d \exp {(\textit{v}_{w_{j’}}^\intercal \cdot \textit{v}_c)}}. $$

Burada, $y_j := p(w_j \mid c)$ ifadesi bağlam kelimesi $c$ verildiğinde çıktı kelimesi $w_j$’nin koşullu olasılığını temsil eder. Bu, $c$ kelimesi göz önüne alındığında $w_j$ kelimesinin ne kadar olası olduğunu gösterir.⁵

Son durumda $\textit{v}_{w_j}$ ve $\textit{v}_c$ vektörlerini öğrenmeyi hedefliyoruz. Bunu gerçekleştirirken kullanacağımız yöntemi özetleyelim.

CBoW modelinin öğrenme süreci, $\textit{W}$ ve $\textit{W}’$ matrislerindeki ağırlıkları güncelleyerek gerçekleşir. Bu güncelleme, eğitim verisindeki bağlam kelime ve hedef kelime çiftlerini modelimize sırayla vererek yapılır. Model, her çift için bir tahmin üretir ve bu tahmin ile gerçek hedef kelimenin olasılığını karşılaştırır. Bu karşılaştırma sonucunda bir kayıp fonksiyonu (loss function) hesaplanır. Kayıp fonksiyonunun gradyanı, her iki ağırlık matrisinin elemanlarına göre bulunur ve bu gradyanın tersi yönünde küçük adımlar atılarak ağırlıklar güncellenir. Bu optimizasyon yöntemine geri yayılım (backpropagation) denir. Esas konudan sapmamak adına bu yöntemin teknik detaylarına girmeyip okurların bu konuda bilgi sahibi olduklarını kabul edeceğiz.

İlk olarak, bir kayıp fonksiyonu $L$ belirleyelim. Bu aşamada notasyonumuzu da güncelleyeceğiz. Hedefimiz, girdi olarak bağlam kelimesi verildiğinde çıktı kelimesinin koşullu olasılığını maksimize etmek olduğundan, kayıp fonksiyonumuzu,

$$L := – \log p(w_{j^*} \mid c)$$
$$= u_{j^*}- \log \sum_{j’=1}^d \exp{(u_{j’})}$$

şeklinde tanımlayacağız ve $L$’yi minimize etmeye çalışacağız. Bu ifadede $j^*$, çıktı katmanındaki gerçek çıktı kelimesinin indisini temsil ediyor.

Bir sonraki aşamada, gizli katman ağırlıkları olan $\textit{W}’$ ve $\textit{W}$ için gereken türevleri bulacağız. Önce, kayıp fonksiyonunun çıktı katmanındaki $j$’inci elemanına göre türevini hesaplayalım:

$$\frac{\partial L}{\partial u_j}= t_j- y_j.$$

Eğer $j=j^*$ ise $t_j= 1$’dir, aksi halde $t_j= 0$’dır. Bu değer, çıktı katmanındaki $j$ bileşeninin tahmin hatasını temsil eder. Notasyonu sadeleştirmek için $e_j := t_j- y_j$ yazacağız.

Şimdi, zincir kuralını kullanarak asıl hedeflediğimiz türevi hesaplayalım:

$$\frac{\partial L}{\partial w’_{ij}}= \frac{\partial L}{ \partial u_j} \cdot \frac{\partial u_j}{\partial w’_{ij}}= e_j h_i.$$

Dolayısıyla, $\textit{W}’$ matrisi için gradyan azalma (gradient descent) denklemimizi, $\eta >0$ öğrenme oranını temsil edecek şekilde şöyle yazabiliriz:

$$w’_{ij}\ ^\text{(yeni)}=w’_{ij}\ ^\text{(eski)}-\eta e_j h_i.$$

Yukarıdaki ifade, ağırlıkların nasıl güncelleneceğini gösterir. Bunu vektörel biçimde yazmak da münkündür:

$$\textit{v}_{w_j}^{\text{(yeni)}}=\textit{v}_{w_j}^{\text{(eski)}}- \eta e_j \textit{h}.$$

Gradyan azalma yöntemi, bir fonksiyonun minimum değerini bulmak için kullanılan bir optimizasyon algoritmasıdır. Bu yöntemde, fonksiyonun gradyanı, yani türevi, arama yönünü belirler. Fonksiyonun gradyanı, fonksiyon değerinin hangi yönde en hızlı arttığını gösterir. Dolayısıyla, gradyanın tersi yönü, fonksiyonun en hızlı azaldığı yönü belirtir. Bu sebeple, gradyanın ters yönünde küçük adımlar atarak fonksiyonun minimum değerine yakınsamaya çalışırız.

Son olarak, $\textit{W}$ matrisinin ağırlıkları için benzer hesaplamalar yapacağız:

$$\frac{\partial L}{\partial h_i}= \sum_{j=1}^d \frac{\partial L}{\partial u_j}\cdot \frac{\partial u_j}{\partial h_i}= \sum_{j=1}^d e_j w’_{ij} := z_i.$$

Burada, girdileri $z_i$ olan $p \times 1$ boyutlu $\textit{z}$ vektörünü, korpustaki tüm kelimelerin çıktı vektörlerinin tahmin hatalarına göre ağırlıklandırılmış toplamı olarak tanımladık.

Son türevimizi hesaplamadan önce, $\textit{h}$ vektörünün giriş katmanından gelen değerler üzerinde doğrusal bir hesaplama gerçekleştirdiğini hatırlayalım:

$$h_i = \sum_{k=1}^d x_k w_{ki}.$$

Bu ifadenin yardımıyla, zincir kuralını kullanarak aşağıdaki hesabı yapabiliriz:

$$\frac{\partial L}{\partial w_{ki}}= \frac{\partial L}{ \partial h_i} \cdot \frac{\partial h_i}{\partial w_{ki}}= z_i x_k.$$

Daha genel bir şekilde aşağıdaki ifadeyi yazabiliriz:

$$\frac{\partial L}{\partial \textit{W}}= \textit{x} \cdot \textit{z}^\intercal.$$

Öte yandan $\textit{x}$ vektörünün sadece tek bileşeni sıfırdan farklı olduğundan, $\frac{\partial L}{\partial \textit{W}}$’nin yalnızca tek satırı sıfırdan faklıdır ve bu satır $\textit{z}^\intercal$ vektöründen başkası değildir.

Sonuç olarak $\textit{W}$ matrisi için gradyan azalma denklemini şu şekilde yazabiliriz:

$$\textit{v}_{c}^{\text{(yeni)}}=\textit{v}_{c}^{\text{(eski)}}-\eta \textit{z}^\intercal.$$

Gradyan azalma algoritmasını uygularken $\textit{W}$ ve $\textit{W}’$ matrisleri rasgele başlatılır. Bu matrislerin elemanları, ortalama değeri sıfır ve varyansı çok küçük olan normal dağılımdan örneklenerek seçilir. Matematiksel olarak, bu durum şu şekilde ifade edilir:

$$w^{(0)}_{ij} \sim \mathcal{N}(0,\epsilon^2), \quad {w’}^{(0)}_{ij} \sim \mathcal{N}(0,\epsilon^2).$$

Burada $\epsilon^2$ varyansı temsil eder ve genellikle $0,01$ gibi küçük bir değer seçilir. Algoritma devam ettikçe, bu matrislerin değerleri güncellenir. Her iterasyonda kayıp fonksiyonun azalması beklenir, kayıp fonksiyon değeri değişiminin belirli bir eşiğin altına düşmesi halinde algoritma sonlanır.

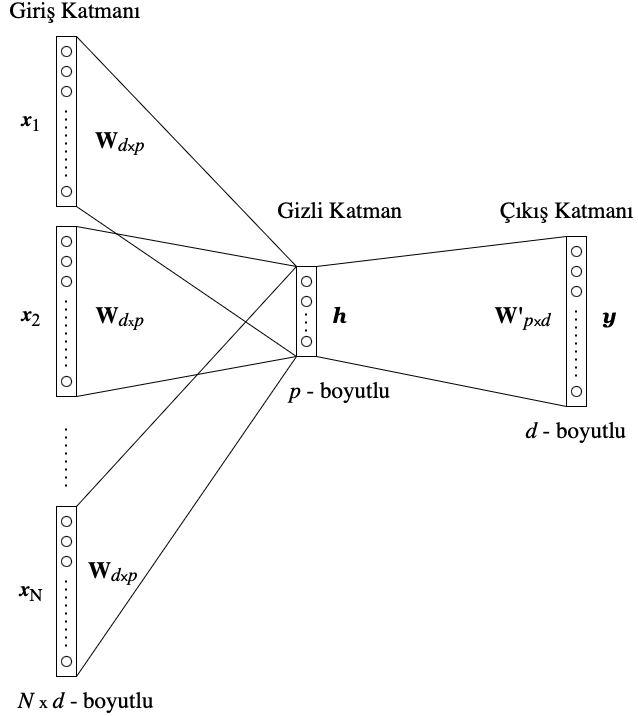
Yazımızın başında, CBoW modelini kurarken tek bir bağlam kelimesi durumu üzerinde duracağımızı belirtmiştik. Fakat birden fazla bağlam kelimesi mevcut olduğunda, örneğin $N$ tane, gizli katman vektörünü bağlam kelimelerinin ortalaması olarak tanımlamamız gerekir:

$$\textit{h}= \frac{1}{N} \textit{W}^\intercal (\textit{x}_1 + \cdots + \textit{x}_N).$$

Bu durumda, kayıp fonksiyonu ve gradyanların formülleri değişse de temel mantık aynı kaldığı için hesaplamalar tek katmanlı modele benzer şekilde yapılabilir.

Örnek

$50$ kelimelik bir korpusumuzun olduğunu varsayalım ve aşağıdaki cümleyi ele alalım:

“Cumhuriyetimizin 100. yılı kutlu olsun!”

Hedef kelimeyi “yıl” olarak seçelim ve pencere boyutunu 2 olarak belirleyelim. Bu, “yıl” kelimesini tahmin ederken, önündeki ve arkasındaki 2 kelimeyi (toplamda 4 bağlam kelimesi) kullanacağımız anlamına gelir.

Metin temizliği sonrasında örnek cümledeki bağlam kelimelerini $50 \times 1$ boyutlu standart baz vektörleriyle ifade edelim:⁶

$$
\begin{aligned}
\text{cumhuriyet}: & \quad \begin{bmatrix}
1 & 0 & 0 & 0 & 0 & \cdots & 0
\end{bmatrix}^\intercal := \textit{x}_1 \\
\text{yüz}: & \quad \begin{bmatrix}
0 & 1 & 0 & 0 & 0 & \cdots & 0
\end{bmatrix}^\intercal := \textit{x}_2\\
\text{kutlu}: & \quad \begin{bmatrix}
0 & 0 & 0 & 1 & 0 & \cdots & 0
\end{bmatrix}^\intercal := \textit{x}_4\\
\text{ol}: & \quad \begin{bmatrix}
0 & 0 & 0 & 0 & 1 & \cdots & 0
\end{bmatrix}^\intercal := \textit{x}_5\\
\end{aligned}
$$

Bu örnekte $N=4$ olduğundan ortalama kelime girdi vektörü aşağıdaki gibi yazılabilir:
\begin{aligned}
\textit{x}_{50 \times 1}= \begin{bmatrix} 0,25 & 0,25 & 0 & 0,25 & 0,25 & \cdots & 0 \end{bmatrix}^\intercal\ \end{aligned}

Bu vektörü iki boyutlu bir uzaya indirgemek için, rasgele bir ağırlık matrisi $\textit{W}$ seçelim:
\begin{equation*} \textit{W}_{50\times2} = \begin{bmatrix}
0,10 & -0,12 \\
0,21 & -0,64 \\
\vdots& \vdots \\
-0,14 & 0,92 \\
0,50 & 0,77 \\
\end{bmatrix}
\end{equation*}

Şimdi bu matrisle ortalama kelime girdi vektörünü çarpalım ve oluşacak $2 \times 1$ boyutlu gömme vektörünü $\textit{h}$ olarak adlandıralım:
\begin{equation*} \textit{W}^\intercal \textit{x} = \begin{bmatrix} 0,1675 & 0,2325 \end{bmatrix}^\intercal = \textit{h}. \end{equation*}

Gömme vektörünü $50$ boyutlu bir uzaya geri yansıtıp çıktı kelime vektörünü elde etmek için $\textit{W}’$ diyeceğimiz rasgele bir ağırlık matrisi seçelim:
\begin{equation*} \textit{W}’_{2\times 50} = \begin{bmatrix} 0,53 & 0,23 & \cdots & 0,50& -0,13 \\ 0,42& -0,70 & \cdots & -0,32 & 0,76 \\ \end{bmatrix}. \end{equation*}

Bu ağırlık matrisini gömme vektörüyle çarpacağız ve hesapladığımız $50 \times 1$ boyutlu çıktı vektörünü $\textit{u}$ ile temsil edelim:
\begin{equation*} \textit{W}’^\intercal \textit{h} = \begin{bmatrix} 0,186 & -0,124 & \cdots & 0,009 & 0,154 \end{bmatrix}^\intercal = \textit{u}. \end{equation*}

Son adımda, $\textit{u}$ vektörüne softmax fonksiyonu $\phi$ uygulayarak korpustaki her bir kelimenin olasılık dağılımını temsil eden $\textit{y}$ vektörünü hesaplayalım:

\begin{equation*} \textit{y}= \begin{bmatrix} 0,02 & 0,05 & 0,05 & 0,07 & 0,08 & \cdots & 0,07 \end{bmatrix}^\intercal. \end{equation*}

Hedef vektörümüz, “yıl” kelimesine denk gelen $50 \times 1$ boyutlu standart baz vektörüdür. Bu vektörde “yıl” kelimesine karşılık gelen indis 1 değerine sahipken, diğer tüm indisler 0 değerine sahiptir.

Modelimiz, tahmin vektörü $\textit{y}$ ile hedef vektör arasındaki hatayı minimize etmeye çalışır. Bunu gerçekleştirmek için, ağırlık matrisleri $\textit{W}$ ve $\textit{W}’$’nin değerlerini geri yayılım yöntemiyle günceller. Geri yayılım algoritması, $\textit{y}$ vektörünün “yıl” kelimesine karşılık gelen elemanının 1’e ve toplam hata teriminin de 0’a yakınsamasını sağlar (Görsel 5). Bu sayede, “yıl” kelimesinin diğer kelimelerle olan ilişkisi en doğru şekilde modellenmiş olur.

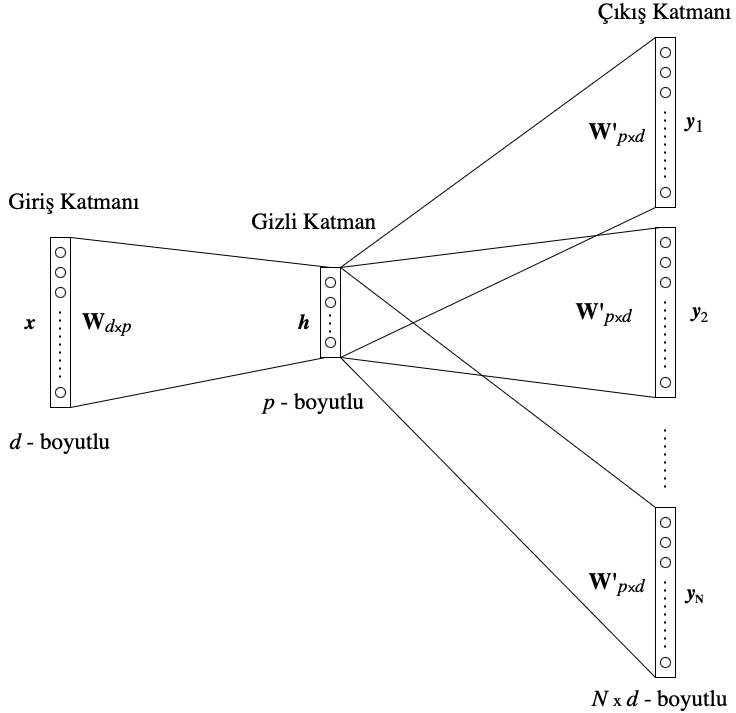
Skip-Gram Modeli

Skip-Gram modeli, önceki bölümde ele alınan CBoW modelinin aksine, belirli bir pencere boyutu içinde yer alan tüm bağlam kelimelerini, verilen bir merkez kelimeye göre tahmin etmeye çalışır (Görsel 6). Matematiksel açıdan bakıldığındaysa Skip-Gram’ın analizi CBoW hesaplamalarıyla benzerlikler gösterir. Bu nedenle, bu bölümde direkt olarak [1]’ye referans vereceğiz.

Hesaplama Verimliliği Optimizasyonu

CBoW ve Skip-Gram modellerinde, her eğitim örneği için sözlükteki her kelime üzerinden döngü yapmak oldukça maliyetli bir işlemdir. Bu işlem, softmax fonksiyonunun payda kısmında gerçekleştirilir ve büyük sözlükler veya büyük eğitim veri kümeleriyle çalışırken zorluk yaratabilir.

Hesaplama maliyetini azaltmak için iki temel yöntem kullanılır: hiyerarşik softmax (hierarchical softmax) ve negatif örnekleme (negative sampling). Bu yöntemlerin matematiksel analizi oldukça ilgi çekicidir. Hevesli okurlara kaynak makaleyi [2] incelemelerini tavsiye ederiz.

Kaynaklar
[1] Xin Rong. word2vec Parameter Learning Exp-lained. 2016. arXiv: 1411.2738 [cs.CL]. 6
[2] Tomas Mikolov ve diğ. Distributed Representa- tions of Words and Phrases and their Compo- sitionality. 2013. arXiv: 1310.4546 [cs.CL].

1. Semantik: Kelimelerin, ifadelerin veya sembollerin anlamını inceleyen bir dilbilim alt dalı. ↩︎
2. Korpus: Külliyat, belli bir alana odaklı büyük ve temsilci kelime dağarcığı. ↩︎
3. Frekans: Bir kelimenin bir metinde geçme sıklığı. ↩︎
4. Gösterim kolaylığı açısından kelimeleri art arda sıralı kabul ediyoruz. ↩︎
5. Burada $\textit{y}$ vektörü de $\textit{x}$ gibi $d \times 1$ boyutludur; ancak one-hot değil, olasılık vektörü belirtir. Bileşenleri $y_i \geq 0$ olmak üzere $\sum_{i=1}^d y_i=1$. ↩︎
6. Gösterim kolaylığı açısından kelimeleri art arda sıralı kabul ediyoruz. ↩︎