Yazar: Eda Aydemir Kayacan (edaaydemir@gmail.com)
Yıl: 2023-1
Sayı: 115
Dünyanın birçok yerinde, kesirler konusu ilköğretim matematik müfredatlarında geniş yer tutmaktadır. Çoğu zaman kullanılan örneklerin günlük hayattan uzak olması nedeniyle, öğrencilerin somutlaştırmakta zorlandığı bu konunun, günümüzden 4000 yıl önce, insanların günlük ihtiyaçları doğrultusunda nasıl şekillendiğine bir bakalım.
Hiyeroglifteki Kesirler aktivitesi, herhangi bir çokluğun “1” parçası kavramından yola çıkarak,
ilkokul çağlarındaki öğrenciler için kesirleri karşılaştırma, sadeleştirme, denk kesirleri belirleme ve kesirlerde dört işlem konularında pratik yapma olanağı sağlarken, daha ileri sınıflardaki öğrenciler için, genelleme yapma ve konuyla ilgili teoriler üzerinde çalışma imkânı sunmaktadır.
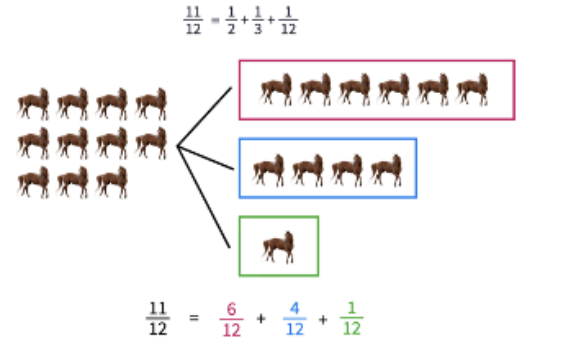
Öğrencilere birçok farklı versiyonu olan ‘‘Yaşlı Adamın Vasiyeti’’ bulmacasını sorarak Hiyeroglifteki Kesirler aktivitesine başlayabilirsiniz: 12 atı ve 3 çocuğu olan yaşlı bir adam, atlarının 1/2’sini kızına, 1/3’ünü ilk oğluna ve 1/12’sini ikinci oğluna bırakmak için vasiyetini yazdı. Ancak yaşlı adam öldükten hemen sonra atlarından biri de ölür. Çocuklar vasiyetin şartlarını yerine getirebilmek için kalan 11 atı nasıl paylaşabilirler?
Bu aktivitenin sonunda, öğrenciler bu ve benzeri bir çok bulmacayı çözmek için gereken yaklaşımı da geliştirmiş olacaklardır.
Hiyeroglifteki Kesirler
Eski Mısırlılar, harfleri ve sayıları temsil etmek için hiyeroglif adı verilen semboller kullanırdı. 10’un pozitif kuvvetleri için kullandıkları bazı semboller:
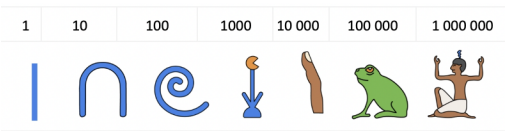
Bu sembolleri tekrarlı kullanarak tüm sayıları yazabiliyorlardı. Örneğin:

Öğrenciler de farklı sayıları hiyeroglif kullanarak yazmayı deneyebilirler.
– Verilen QR kodu okutup, öğrencilerin Polypad kullanarak sayıları yazmasını ya da
– Her öğrencinin küçük bir kâğıda hiyeroglifleri kullanarak bir sayı yazmasını, bunu bir arkadaşı ile değiştirerek, sayıları çözmelerini isteyebilirsiniz.

Eski Mısırlılar, sayı sembolünün üzerine “kısım” anlamına gelen ve R harfi için kullanılan oval (ağız simgesi) yerleştirerek kesirleri de hiyeroglif kullanarak yazmışlardır.

Mısırlılar bu notasyonla$^1$ tüm birim kesirleri yazabiliyorlardı. Ancak en şaşırtıcı kısım, günümüzden 4000 yıl önce, Mısırlıların birim kesirleri kullanarak TÜM kesirleri de yazabilmeleriydi.
Eski Mısırlılar yalnızca birim kesirleri yazmak için semboller kullanmışlardır, bu nedenle diğer kesirleri birim kesirlerin toplamı olarak ifade etmişlerdir.
$\frac{5}{6}$ gibi bir kesri ele alalım; $\frac{5}{6}$ kuşkusuz, $$\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}$$ şeklinde yazılabilir. Ama bu çok fazla sembol gerektireceğinden ve çok yer kaplayacağından çok da pratik bir ifade şekli olmayacaktır.
Öğrencilere $\frac{5}{6}$ kesrini daha az sayıda birim kesrin toplamı şeklinde yazıp yazamayacaklarını sorabilirsiniz.
Olası cevaplardan biri $\frac{1}{2}+\frac{1}{3}$ toplamıdır.
QR kodu okutarak, öğrencilerden $\frac{1}{2}+\frac{1}{3}$ toplamını yani $\frac{5}{6}$ kesrini hiyeroglif ile yazmalarını ve $\frac{5}{6}$ kesrini bu şekilde ifade etmenin avantaj ve dezavantajlarını tartışmalarını isteyebilirsiniz.


Bu işlemi, 5 ekmeği 6 kişi arasında paylaştırma problemi gibi düşünelim. 5÷6 işleminin ondalık karşılığı gündelik hayatta ekmeğin bölünmesine bir yardım sağlamayacaktır. $\frac{5}{6}$ kesriyse sadece bölümün başka bir sembolle ifadesidir. Bu işlemi görselleştirerek, $\frac{5}{6}$ kesrini, $\frac{1}{2}+\frac{1}{3}$ şeklinde ifade etmenin, 4000 yıl önce Mısır’da, günlük hayatta karşılaşılan problemlerin çözümü için nasıl daha pratik bir yöntem olduğunu daha iyi görebiliriz.
Bu tartışma sırasında öğrencilerin bu yazım şekliyle ilgili neleri merak ettiklerini de sorarak, bu çalışmanın geri kalanı için şu sorgulamaları yapmalarını teşvik edebilirsiniz;
- $\frac{5}{6}$ kesri başka şekillerde de birim kesirlerin toplamı şeklinde yazılabilir mi?
- Her kesir birbirinden farklı $^a$ birim kesirlerin toplamı şeklinde ifade edilebilir mi?
- Eğer bir kesir birden fazla değişik şekilde birim kesirlerin toplamı olarak yazılabilirse, en pratik yazma şeklini nasıl bulabiliriz?
İlk sorgulamaya yardımcı olmak için öğrencilere şu soruları yöneltebilirsiniz.
$$\frac{1}{2}+\frac{1}{4}+\frac{1}{?}=\frac{5}{6} \quad\quad \frac{1}{3}+\frac{1}{4}+\frac{1}{?}=\frac{5}{6}$$
$^a$ Mısırlıların yöntemiyle kesirleri yazarken, birim kesirlerin birbirinden farklı olduğu durumlara odaklanalım.
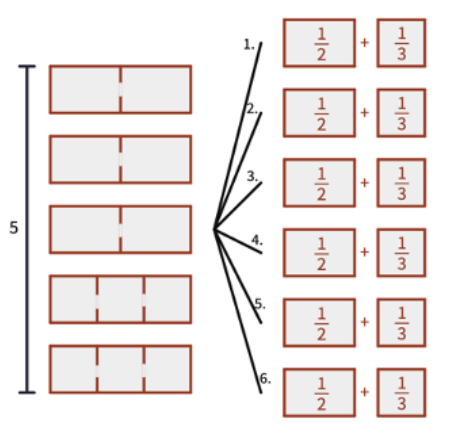
Öğrencilerin hazır bulunuşluk düzeylerine göre, ikinci sorgulamaya geçmeden, kesir şeritleri kullanarak farklı kesirleri birim kesir toplamı şeklinde yazmalarını tavsiye edebilirsiniz.
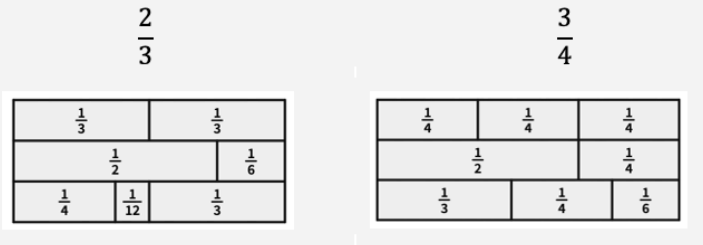

Öğrenciler, tüm kesirlerin, birim kesirlerin toplamı şeklinde ifade edilebilirliğini araştırırken sistematik bir yaklaşımla tüm kesirleri tahtaya yazarak ilerleyebilir ya da istasyon çalışması yapabilirsiniz. Öğrencileri mümkün olduğu kadar çok sayıda farklı toplamın yanı sıra mümkün olan en az sayıda birim kesre sahip toplamı da bulmaya teşvik edebilirsiniz.
Örneğin;
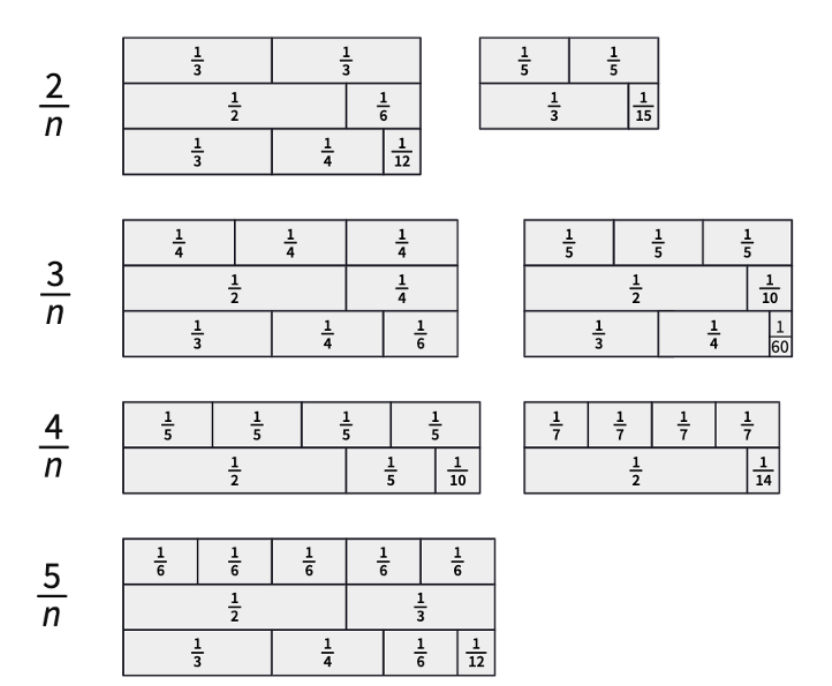
Bir Birim Kesri Farklı İki Birim Kesrin Toplamı Şeklinde İfade Etme
Öğrenciler herhangi bir birim kesir $\frac{1}{n} (n\not = 0,n\not =1)$ için, $\frac{1}{n+1}$ kesrinin $\frac{1}{n}$’den küçük, en büyük birim kesir olarak kullanılabileceğini fark edebilirler. Örneğin
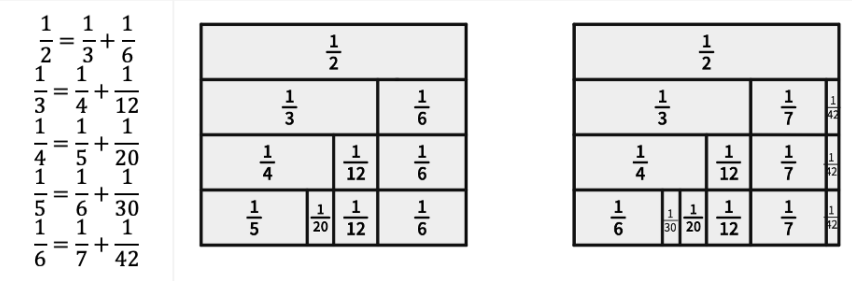
Böylece herhangi bir birim kesri, başka birim kesirlerin toplamı olarak yazmak için sonsuz sayıda seçenek olduğu gösterilebilir. Bu yöntem, öğrencilerin sınıf düzeylerine göre
$\frac{1}{n}=\frac{1}{n+1}+\frac{1}{(n(n+1)}$ şeklinde ifade edilerek genelleme yapılabilir.
Daha ileri sınıflardaki öğrenciler de tüm olası birim kesir çiftlerini bulabilmek için rasyonel denklemlerden yararlanabilirler.
$\frac{1}{n}=\frac{1}{n+a}+\frac{1}{n+b}\quad (a\cdot b = n^2 , n\not =0)$ eşitliğini kullanalım. Örneğin $\frac{1}{6}$ kesrini düşünelim. ($6^2=36$) 36 çarpımını verebilecek pozitif tamsayı çiftleri (1, 36), (2, 18), (3, 12) , (4, 9) ve (6, 6)’dır.
$$\begin{align}\frac{1}{6} & = \frac{1}{6 +1} +\frac{1}{6 + 36} = \frac{1}{7} + \frac{1}{42},\\
\frac{1}{6} & = \frac{1}{6 +2} +\frac{1}{6 + 18} = \frac{1}{8} + \frac{1}{24},\\
\frac{1}{6} & = \frac{1}{6 +3} +\frac{1}{6 + 12} = \frac{1}{9} + \frac{1}{18},\\
\frac{1}{6} & = \frac{1}{6 +4} +\frac{1}{6 + 9} = \frac{1}{10} + \frac{1}{15},\\
\frac{1}{6} & = \frac{1}{6 +6} +\frac{1}{6 + 6} = \frac{1}{12} + \frac{1}{12},\end{align}$$
şeklinde yazılabilir.
Bu çalışmadan sonra, öğrencilere payı 1’den farklı kesirleri, birim kesirlerin toplamı şeklinde yazmak için hangi stratejileri kullandıklarını sorabilirsiniz.
Birim Kesirleri Bulma Stratejileri
En az sayıda veya mümkün olan en küçük paydaya sahip birim kesir toplamlarını yazabilmek için hiçbir algoritma bilinmemektedir (Hoffman 1998, s. 155). Bununla birlikte, farklı kesirleri, birim kesirlere ayrıştırmak için farklı yöntemler, algoritmalar kullanılabilir.$^2$
Bazı kesirler sezgisel olarak kolayca farklı birim kesirlerin toplamı şeklinde yazılabilir. Eğer orijinal kesirin payı, paydanın çarpanlarının toplamı şeklinde yazılabiliyorsa, birim kesirler çoğu zaman kolaylıkla bulunabilir.
Örneğin,
$$\begin{align}
\frac{5}{36} & = \frac{4}{36} + \frac{1}{36} \Rightarrow \frac{5}{36} = \frac{1}{9} + \frac{1}{36} \\
\frac{9}{80} & = \frac{8}{80} + \frac{1}{80} \Rightarrow \frac{9}{80} = \frac{1}{10} + \frac{1}{80} \\
\frac{9}{42} & = \frac{7}{42} + \frac{2}{42} \Rightarrow \frac{9}{42} = \frac{1}{6} + \frac{1}{21}\\
\frac{9}{20} & = \frac{4}{20} + \frac{5}{20} \Rightarrow \frac{9}{20} = \frac{1}{5} + \frac{1}{4}\end{align}$$
Orijinal kesri mümkün olan en az sayıda birim kesirle ifade edebilmek için, verilen kesirden küçük en büyük birim kesri bulmak gerekir.
Birim kesirleri bulabilmek için, (en büyük birim kesir 1/2 olduğu için) öğrenciler öncelikle orijinal kesri yarımdan büyük veya küçük olarak sınıflandırabilirler.
Aslında bu yönteme Fibonacci’nin Açgözlü Algoritması (Greedy Algorithm) denir. Her seferinde kalan kısmın içindeki en büyük -ve ilk birim kesirden farklı- birim kesri (açgözlülükle) alırız ve sonra aynı işlemi geri kalan kesir için tekrarlarız.
Örneğin $\frac{17}{20}$ kesrini ele alalım;$\frac{17}{20} > \frac{1}{2}$ olduğundan ilk adım $\frac{17}{20} – \frac{1}{2} = \frac{7}{20}$ olacaktır.
Geri kalan kısımdan küçük olan en büyük birim kesir $\frac{1}{3}$’tür. İkinci adım; $\frac{7}{20} – \frac{1}{3} = \frac{1}{60}$. Böylelikle;
$$\frac{17}{20} = \frac{1}{2} + \frac{1}{3} + \frac{1}{60}$$ şeklinde yazılabilir.
$\frac{5}{14}$ kesri içinse, alınabilecek en büyük birim kesir ancak $\frac{1}{3}$ olabilir: $\frac{5}{14} – \frac{1}{3} = \frac{1}{42}$. Dolayısıyla $\frac{5}{14}$, $\frac{1}{3} + \frac{1}{42}$ toplamı olarak yazılabilir.
Açgözlü Algoritma çoğu zaman en az sayıda birim kesir toplamını vermeyebilir.
Örneğin $\frac{5}{21}$ kesri, açgözlü algoritmayla $\frac{1}{5} + \frac{1}{27} + \frac{1}{945}$ olarak yazılır, oysaki $\frac{5}{21} = \frac{1}{6} + \frac{1}{14}$ şeklinde daha az sayıda ve daha küçük paydalara sahip birim kesirlerin toplamı olarak da ifade edilebilir.
Bu çalışmayla ilgili ek desteğe ihtiyaç duyan öğrenciler için, genel kurallara odaklanmak yerine, orijinal kesirden çıkarılabilecek en büyük birim kesri bulma çalışmaları yapılabilir.
Bu şekilde, genel kuralları cebirsel olarak yazmadan, yine de herhangi bir kesrin birim kesirlerin toplamı olarak sonsuz şekilde yazılabileceğini kanıtlayabilirler.
Konuya ilgi duyan öğrenciler içinse, şu sorular sorulabilir;
- MÖ 1650’lerden kalma ünlü Rhind papirüsü, 5 ile 101 arasındaki her tek $n$ sayısı için, $\frac{2}{n}$’yi birim kesirlerin toplamı şeklinde ifade eden bir temsil tablosunu içerir. Payı 2 olan kesirler için genel bir yöntem bulunabilir mi?
- 1940’larda ünlü matematikçiler Paul Erdos ve Ernst G. Straus, payı 4 olan her kesrin, üç birim kesrin toplamı olarak yazılabileceğini duyurdular. $\frac{3}{n}, \frac{4}{n}, \frac{5}{n}$ kesirleri için cebirsel bir ifade geliştirilebilir mi?
- Bazı matematikçilerse birim kesirlerin terim sayısı üzerinde çalışmıştır. Siz de 4 birim kesirden daha az birim kesir kullanılarak yazılamayacak bir kesir bulabilir misiniz? Ya da en az 5 birim kesir? (İpucu; her iki örneğin de paydası 20’den küçük!)
Bu çalışmanın sonunda, dersin başındaki bulmacayı öğrencilere hatırlatarak çözüm için tekrar düşünmelerini istemeyi unutmayın!
QR kodu kullanarak, tüm içeriği Desmos Classroom platformunda görüntüleyip, düzenlemeler yapıp, öğrencilerinizle paylaşabilirsiniz.

$^1$ Antik Mısır’da farklı kesir yazma stilleri ile $\frac{1}{2}$ ya da $\frac{3}{4}$ gibi kesirler için kullanılan ve belirtilen kuralın dışında kalan semboller olduğu da bilinmektedir.
$^2$ WOLFRAM Demonstrations Project’in yayınladığı “Algorithms for Egyptian Fractions (Mısır Kesirleri bulma Algoritmaları)” uygulamasını indirerek, her kesir için harmonik ve binary gibi farklı algoritmalarla hesaplanan farklı toplam ifadelerini görebilirsiniz.


