Kolay Yoldan Logaritma

Yazar: Yusuf Avcı, Kâmil Alnıaçık & Nurettin Ergun (İstanbul Üniversitesi Matematik Bölümü öğretim üyeleri)

Yıl: 1995-3

Sayı: 23

Lise öğrencilerine logaritma ve onun ters fonksiyonu olan üstel fonksiyonun sağlıklı ve eksiksiz inşasını vermek doğrusu pek olanaklı değildir. Sözgelimi bir lise öğrencisi $2^{\sqrt{2}}$ sayısının nasıl tanımlandığını pek bilemez. Hemen hemen tüm lise kitaplarında bu konudaki temel bilgiler ispatsız verilir ya da daha yerinde bir deyimle verilmek zorunda kalınır. Biz bu yazıda lise öğrenci ve öğretmenlerine logaritmanın bazı temel bilgilerini kolay ve sağlıklı bir yoldan vermek istiyoruz. En azından $\ln (ab)=\ln a+\ln b$ eşitliğinin kanıtlamasını kavramak için
$$ (i) gerçel (reel) sayıların Arşimet özelliği, yani her pozitif $x$ gerçel sayısı için $x<n$ gerçeklenecek biçimde bir $n$ doğal sayısının varlığı bilgisi ile
$$ (ii) $\sum _{k=1}^n(a_k-a_{k-1})=(a_1-a_0)+\cdots +(a_n-a_{n-1})=a_n-a_0$ gerçeklendiğini söyleyen teleskopik toplam özelliği ve benzeri basit ve temel eşitsizlik bilgileri
yeterli olacaktır.

Doğal Logaritma Fonksiyonu

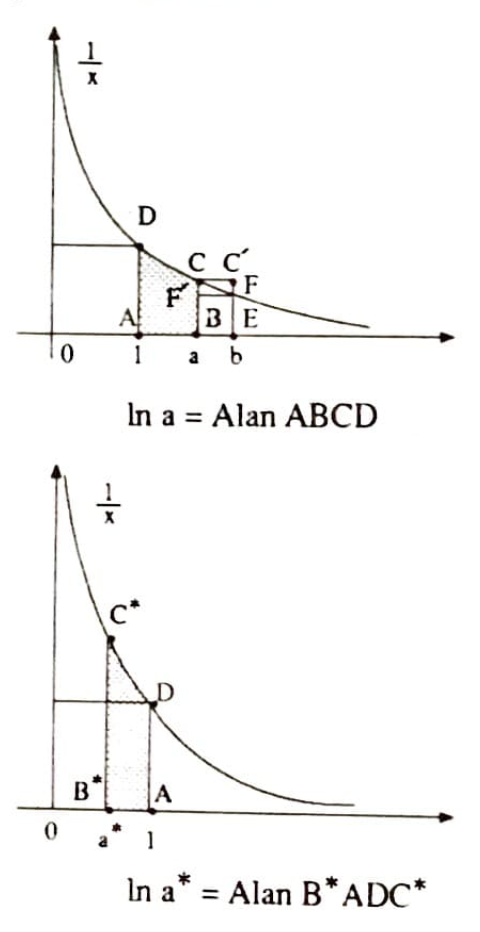
Bu fonksiyon, $f(x)=\frac{1}{x}$ hiperbölünün, düzlemin sağ üst dördünündeki kolu yardımıyla yukarıdaki gibi tanımlanır. Dikkat: yalnızca $0<a$ gercekleyen gerçel sayıların $\ln a$ doğal logaritma değerleri tanımlıdır ve $1\le a$ ya da $a^{\ast }<1$ oluşuna göre bu tanımlama farklı yapılır.

O halde bu tanımlamadan kolayca $\ln 1=0$ elde edilir. Şimdi sırasıyla şunları gözleyelim:

$$ $\mathrm{I}.$ $0<a<b$ ise $\frac{b-a}{b}<\ln b-\ln a<\frac{b-a}{a}$ olur. Üç ayrı durum tek tek irdelenmelidir. Eğer $1\le a<b$ geçerliyse birinci şekil yardımıyla

$$\begin{array}{rl}\ln b-\ln a& =\mathrm{Alan}(AEFD)-\mathrm{Alan}(ABCD)\\ & =\mathrm{Alan}(BEFC)\\ & \{\begin{array}{c}>\mathrm{Alan}(BEF{F}^{\prime })=\frac{b-a}{b}\\ <\mathrm{Alan}(BE{C}^{\prime }C)=\frac{b-a}{a}\end{array}\end{array}$$ bulunur. $a<1\le b$ ve $0<a<b<1$ halleri benzer biçimde kolaylıkla yapılır. Dikkat edilirse $\ln a<\ln b$ olabilmesi için $0<a<b$ gerçeklenmesi gerek ve yeterdir.

$$ $\mathrm{II}.$ $0<a<b$ olsun. Her $n\in \mathbb{N}$ doğal sayısı için $$|\ln \frac{b}{a}-(\ln b-\ln a)|<\frac{(b-a{)}^2}{nab}$$ geçerlidir.

Önce $k=0,1,\dots ,n$ için $a_k=a+\frac{k(b-a)}{n}$ gerçel sayılarını tanımlayalım. Kolaylıkla $a=a_0<a_1<\cdots <a_n=b$ ve $a_k-a_{k-1}=\frac{b-a}{n}$ elde edilir. $\mathrm{I}.$ özelliği kullanılırsa

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\ln b-\ln a& =\sum _{k=1}^n(\ln a_k-\ln a_{k-1})\\ & \{\begin{array}{c}<\sum _{k=1}^n\frac{a_k-a_{k-1}}{a_{k-1}}=\frac{b-a}{n}\sum _{k=1}^n\frac{1}{a_{k-1}}\\ >\sum _{k=1}^n\frac{a_k-a_{k-1}}{a_k}=\frac{b-a}{n}\sum _{k=1}^n\frac{1}{a_k}\end{array}\end{array}\end{array}$$ bulunur. Şimdi de $b_k=\frac{a_k}{a}$ gerçel sayıları tanımlanarak, önce $1=b_0<b_1<b_2<\cdots <b_n=\frac{b}{a}$, $b_k-b_{k-1}=\frac{b-a}{na}$, sonra
$$\begin{array}{rl}\ln \frac{b}{a}=\ln \frac{b}{a}-\ln 1& =\sum _{k=1}^n(\ln b_k-\ln b_{k-1})\\ & \{\begin{array}{c}<\sum _{k=1}^n\frac{b_k-b_{k-1}}{b_{k-1}}\\ >\sum _{k=1}^n\frac{b_k-b_{k-1}}{b_k}\end{array}\end{array}$$
ve dolayısıyla $$\begin{array}{}\text{(2)}& \frac{b-a}{n}\sum _{k=1}^n\frac{1}{a_k}=\frac{b-a}{na}\sum _{k=1}^n\frac{1}{b_k}<\ln \frac{b}{a}<\frac{b-a}{na}\sum _{k=1}^n\frac{1}{b_{k-1}}=\frac{b-a}{n}\sum _{k=1}^n\frac{1}{a_{k-1}}\end{array}$$
elde edilir. $(1)$ ve $(2)$ numaralı eşitsizlikler yardımıyla $$\ln \frac{b}{a}-(\ln b-\ln a)\{\begin{array}{l}<\frac{b-a}{n}\sum _{k=1}^n(\frac{1}{a_{k-1}}-\frac{1}{a_k})\\ >\frac{b-a}{n}\sum _{k=1}^n(\frac{1}{a_k}-\frac{1}{a_{k-1}})\end{array}$$ elde edilir. Sağ yandaki teleskopik toplamlar kolayca hesaplanarak sonuçta $$-\frac{(b-a{)}^2}{nab}<\ln \frac{b}{a}-(\ln b-\ln a)<\frac{(b-a{)}^2}{nab}$$ bulunur ki bu istenenden başka bir şey değildir.

$$ $\mathrm{III}.$ $0<a$ ve $0<b$, ne olursa olsun $$\ln \frac{b}{a}=\ln b-\ln a\text{ve}\ln ab=\ln a+\ln b$$ eşitlikleri geçerlidir. İkincisi birincinin çok kolay bir sonucu olduğundan (neden?) yalnızca birinci eşitliği göstermek yeterli olacaktır. Kısalık amacıyla $A_{ab}=\ln \frac{b}{a}-(\ln b-\ln a)$ yazalım. Önce $0<a\le b$ durumunu irdeleyelim. Eğer $A_{ab}\ne 0$ olsaydı, Arşimet özelliği nedeniyle $$\frac{(b-a{)}^2}{\left|A_{ab}\right|ab}<n_0$$ gerçekleyen bir $n_0$ doğal sayısı var olmak zorunda kalırdı, bu $\mathrm{II}.$ nedeniyle olanaksızdır. Demek ki $0<a\ne b$ iken $\ln \frac{b}{a}=\ln b-\ln a$ geçerlidir. Üstelik

$$\begin{array}{}\text{(3)}& 0<a\text{için}\ln a+\ln \frac{1}{a}=0\end{array}$$
gerçeğini de kolayca gözleyebiliriz. Gerçekten $a=1$ için apaçık olan bu iddia, $0<a<1$ için son gösterilen eşitlik kullanılarak
$$\ln a+\ln \frac{1}{a}=\ln a+(\ln 1-\ln a)=0;$$
$1<a$ olduğunda ise $\frac{1}{a}<1$ için bu son bilgi kullanılarak $$\ln a+\ln \frac{1}{a}=\ln \frac{1}{a}+\ln \frac{1}{1/a}=\ln \frac{1}{a}+\ln 1-\ln \frac{1}{a}=0$$

nedeniyle geçerlidir. O halde $b<a$ için $(3)$ kullanılarak $$\ln \frac{b}{a}=-\ln \frac{1}{b/a}=-\ln \frac{a}{b}=-(\ln a-\ln b)=\ln b-\ln a$$ bulunur. Bitti!

Doğal Logaritmanın Tabanı

$\ln a=1$ gerçekleyen biricik $a$ pozitif gerçel sayısına doğal logaritmanın tabanı denir. Böyle bir gerçel sayının var olduğunu, doğal logaritma fonksiyonunun tanımında, birinci şekildeki $[BC]$ doğrusunu oynatarak kolaylıkla “sezinleyebiliriz”, ama bunu kesin ve sağlıklı bir biçimde “kanıtlamak” ciddi bir iştir, çünkü ciddi ve derin bilgiler kullanmayı gerektirir. Biz bu gerçel sayıyı üstelik “keşfetmek”, daha yerinde bir deyimle İsviçreli usta matematikçi Leonhard Euler’in 250 yıllık yöntemini burada yinelemek istiyoruz.

$$ $\mathrm{IV}.$ Her $n$ doğal sayısı için $$2\le {(1+\frac{1}{n})}^n<{(1+\frac{1}{n+1})}^{n+1}<{(1+\frac{1}{n+1})}^{n+2}<{(1+\frac{1}{n})}^{n+1}\le 4$$ eşitsizlikleri gerçeklenir. Başka bir yazışla ise, $a_n={(1+\frac{1}{n})}^n$ ve $b_n={(1+\frac{1}{n})}^{n+1}=a_n(1+\frac{1}{n})$ şeklindeki rasyonel sayı dizileri $$2=a_1<\cdots <a_n<a_{n+1}<b_{n+1}<b_n<\cdots <b_1=4$$ gerçekler. Gerçekten ünlü Bernoulli eşitsizliğini [1], yani $$1+nx<(1+x{)}^n(n\in \mathbb{N},-1<x,x\ne 0)$$ kullanırsak, $n(n+2)<(n+1{)}^2$ yardımıyla $$\begin{array}{rl}1+\frac{1}{n+1}& <1+(n+1)\frac{1}{n(n+2)}\\ & <{(1+\frac{1}{n(n+2)})}^{n+1}\\ & ={\left(\frac{1+\frac{1}{n}}{1+\frac{1}{n+1}}\right)}^{n+1}\\ & =\frac{b_n}{a_{n+1}},\end{array}$$ ve sonuçta $b_{n+1}=(1+\frac{1}{n+1})a_{n+1}<b_n$ bulunur. Benzer biçimde $$\begin{array}{rlr}\frac{1}{1+\frac{1}{n+1}}& =1-\frac{1}{n+2}<1-n\frac{1}{(n+1{)}^2}& <{(1-\frac{1}{(n+1{)}^2})}^n=\frac{{(1+\frac{1}{n+1})}^n}{a_n},\end{array}$$ ve sonuçta $a_n<(1+\frac{1}{n+1}){(1+\frac{1}{n+1})}^n=a_{n+1}$ bulunur. $a_{n+1}<b_{n+1}$ eşitsizliği ise apaçıktır. Yukarıdaki eşitsizlikleri elde etmenin güçlük neresinde diye sorabilirsiniz. Hayır, bunlar gercekten güç değildir. Güçlük bundan sonra başlar. Gerçel sayılara ilişkin ve aslında birbirlerine eşdeğer olan bazı temel bilgiler şunları söyler $($$a_n$ ve $b_n$ rasyonel sayıları yukarda tanımlananlar olmak üzere$)$:

$$ (iii) Tüm bu $[a_n,b_n]$ aralıklarına ait olabilen tek bir gerçel sayı vardır (Cantor iç içe azalan aralıklar özelliği), çünkü bu aralıkların uzunlukları olan ${\delta }_n=b_n-a_n$ sayları $a<{\delta }_n=\frac{a_n}{n}<\frac{4}{n}$ nedeniyle $\underset{n\to \mathrm{\infty }}{lim}{\delta }_n=0$ gerçekler.

$$ (iv) Ya da $A=\{a_1,a_2,\dots \}$ sonsuz elemanlı üstten sınırlı kümesi ile $B=\{b_1,b_2,\dots \}$ alttan sınırlı kümesi için $supA=infB$ gerçeklenir (supremum özelliği), çünkü $supA\le infB$ geçerli olup, $supA<infB$ gerçeklenemez. Bunu göstermeye çalışmanızı öneririz!

$$ (v) Ya da üstten sınırlı ve monoton artan ${\left\{a_n\right\}}_{n=1}^{\mathrm{\infty }}$ dizisi ile alttan sınırlı ve monoton azalan ${\left\{b_n\right\}}_{n=1}^{\mathrm{\infty }}$ dizileri yakınsaktır ve $\underset{n\to \mathrm{\infty }}{lim}{a}_n=\underset{n\to \mathrm{\infty }}{lim}{b}_n$ gerçeklenir (monoton ve sınırlı dizilerin yakınsaklığı özelliği). Neden bu iki limit eşittir?

İşte, $\bigcap _{n=1}^{\mathrm{\infty }}[a_n,b_n]$ kesişim kümesinin biricik elemanı olan ya da $$supA(=infB=\underset{n\to \mathrm{\infty }}{lim}{a}_n=\underset{n\to \mathrm{\infty }}{lim}{b}_n)$$ eşitliklerini gerçekleyen biricik gerçel sayı, matematikte onu ilk tanımlayan Euler’in anısına saygı olarak $e$ işareti ile gösterilir. Matematiğin bu ikinci en ünlü irrasyonel sayısının, rasyonel katsayılı hiç bir polinomun kökü olamadığı gerçeğini ilk kez 1874 yılında Fransız matematikçi Charles Hermite kanıtlamıştır. Bu irrasyonel sayının ondalık açılımındaki ilk basamakları $$e=2,71828182859045\cdots$$ şeklindedir. ${}^1$

$$ $\mathrm{V}.$ Şimdi $\ln e=1$ gerçeklendiğini artık gösterebiliriz. $\ln ab=\ln a+\ln b$ özelliğinin bir sonucu olan $\ln a^n=n\ln a$ eşitliği, tümevarımla kolayca gösterilebilir. $\mathrm{I}.$ özelliği nedeniyle $$\frac{1}{n+1}<\ln (1+\frac{1}{n})=\ln (1+\frac{1}{n})-\ln 1<\frac{1}{n}$$ kullanılarak kolayca $$\begin{array}{}\text{(4)}& \frac{n}{n+1}<\ln a_n=n\ln (1+\frac{1}{n})<1\end{array}$$ elde edilir. Üstelik $a_n<e<b_n$ nedeniyle $$\begin{array}{}\text{(5)}& \ln a_n<\ln e<\ln b_n=\frac{n+1}{n}\ln a_n\end{array}$$ geçerlidir. Burada bir başka bilgi, limitlerdeki ünlü sıkıştırma bilgisi kullanılıp $(4)$ ve $(5)$ bağıntılarında limit alınarak kolayca $$1=\underset{n\to \mathrm{\infty }}{lim}\ln a_n\le \ln e\le \underset{n\to \mathrm{\infty }}{lim}((1+\frac{1}{n})\ln a_n)=1,$$ yani $\ln e=1$ sonucu elde edilir.

Şaşırtıcı Limit

Herhangi bir $X$ gerçel sayısının bir logaritmik değer olduğunu, yani tek bir pozitif $x$ gerçel sayısı sayesinde $X=\ln x$ gerçeklendiğini; $\underset{n\to \mathrm{\infty }}{lim}{r}_n=X$ gerçekleyen herhangi bir ${\left\{r_n\right\}}_{n=1}^{\mathrm{\infty }}$ rasyonel sayılar dizisi sayesinde $$\underset{n\to \mathrm{\infty }}{lim}{(1+\frac{X}{n})}^n=\underset{n\to \mathrm{\infty }}{lim}{(1+\frac{1}{n})}^{n{r}_n}$$ şaşırtıcı limit işleminin gerçeklendiğini ve işte bu limit değerinin yukarıdaki eşitliği gercekleyen pozitif $x$ gerçel sayısı olduğunu kanıtlamadan yalnızca söylemekle yetinelim. Bu $x$ pozitif sayısının varlığını kanıtlamanın daha başka yolları da vardır. Bütün bunları Analiz kitaplarına bırakıyoruz.

KAYNAKÇA

[1] N. Ergun, Gerçel Sayılarda Dokuz Temel Eşdeğerlik, Matematik Dünyası, 4, sayı 5, 6-10 (1994).

${}^1{\left\{a_n\right\}}_{n=1}^{\mathrm{\infty }}$ dizisinin yüz milyonuncu terimini bilgisayar yardımıyla hesaplayın! Ne buldunuz?

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 3. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.