Yazar: Eda Aydemir Kayacan – edaaydemir@gmail.com
Yıl: 2024-1
Sayı: 119
Fibonacci(1170-1250)
Orta çağın en büyük matematikçilerinden biri olan Fibonacci, (Leonardo of Pisa, Leonardo Pisano) modern aritmetiğin temellerini batı dünyasına tanıtan Liber Abaci‘yi (Hesaplama Kitabı) yazmasıyla tanınır.
Fibonacci çocukluğunu babasının görevli olduğu Kuzey Afrika’da geçirdi. 1200 yılında Pisa’ya dönene kadar Mısır, Suriye, Yunanistan, Sicilya ve Provence’ta bulundu. Fibonacci, Cezayir’de gördüğü eğitim sırasında Hint-Arap rakam sistemi ile tanıştı. Çok geçmeden Hindu-Arap rakamlarıyla aritmetiğin Roma rakamlarıyla olduğundan çok daha basit ve pratik olduğunu fark etti. Daha sonra, 1202’de bulgularını, Avrupa’da Hindu-Arap rakamlarını popülerleştiren en tanınmış eserlerinden biri olan Liber Abaci‘de yayımladı.
Liber Abaci
14. yüzyıldan kalma bir kopyası Floransa Ulusal Kütüphanesi’nde olan Liber Abaci‘nin, Kansas, Amerika’daki Linda Hall Kütüphanesi tarafından paylaşılan dijital kopyasına buradan ulaşabilirsiniz.

Liber Abaci ile ilgili bir diğer enteresan bilgi de çok yakın bir tarihe kadar bu kitabın Latince’den bir çevirisinin olmamasıdır. 2002 yılında, Bucknell Üniversitesi matematik profesörü Laurence Sigler tarafından İngilizceye çevrilip Leonardo Pisano’s Book of Calculation adıyla yayımlanmıştır.
Liber Abaci‘de yer alan problemden biri olan Tavşan Popülasyonu Problemi, aslında Hintli matematikçiler tarafından yüzyıllar öncesinden beri bilinen ünlü bir sayı dizisinin batı dünyasında yaygınlaşmasını sağlamıştır.
Günümüzde Fibonacci sayı dizisi olarak bilinen, $1, 1, 2, 3, 5, 8, 13, 21, …$ sayı dizisi, aslında 1877 yılında matematikçi Edouard Lucas diziye bu ismi verene kadar, Fibonacci dizisi olarak anılmıyordu.
Tavşan Popülasyonu Problemi
Probleme göre, bir çift tavşan doğduktan bir ay sonra çiftleşerek, ikinci ay bir çift daha tavşan üretebilir. Tavşanlarımızın asla ölmediğini ve dişinin ikinci aydan sonraki her ay yeni bir çift (bir erkek, bir dişi) tavşan ürettiğini varsayalım. Belirli bir ayda kaç çift tavşan olacaktır?
İlk ay 1 çift tavşan, ikinci ay hâlâ 1 çift, üçüncü ay yeni bir çift tavşan doğacağı için, çift sayısı 2’ye yükselir. Dördüncü ay ilk çift 1 çift tavşan daha doğurur ve toplam çift sayısı 3’e yükselir. Buradaki tabloda çift sayılarının ileriki aylarda 5 ve 8’e ulaştığını görebiliriz.
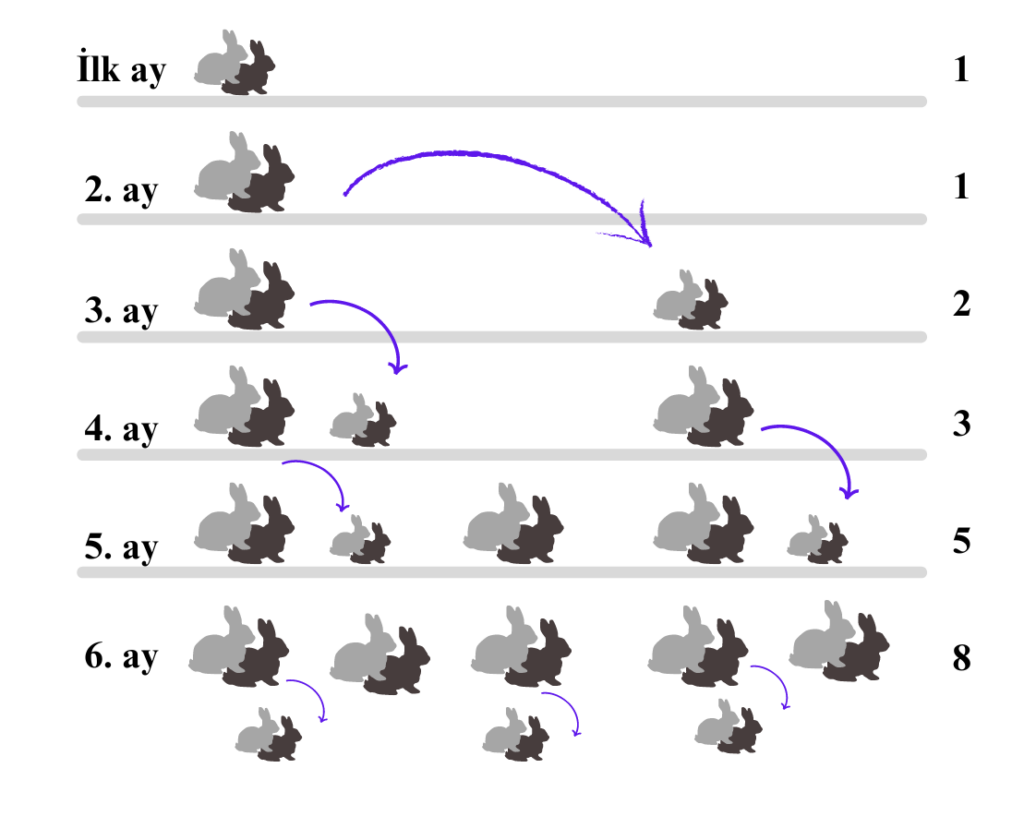
Belirli bir aydaki tavşan sayısı önceki iki sayının toplamıdır. Başka bir deyişle, bir sonrakini elde etmek için dizideki önceki iki terimi eklemeniz gerekir.
$$x_n=x_{n-1}+x_{n-2}$$
Fibonacci dizisi, basit bir doğrusal yineleme ilişkisiyle tanımlanan bir tamsayı dizisidir. Fibonacci sayıları, her bir terimin önceki iki terimin toplamı olduğu bir tamsayı dizisinin terimleridir.
$$ F_1 = F_2 = 1\text{, }F_n =F_{n-1} +F_{n-2}$$
Elbette Fibonacci sayıları, gerçek hayattaki tavşan popülasyonunu tam olarak yansıtmaz. (Tavşanların her ay tam olarak bir erkek ve bir dişi yavrusu olması ve ölümsüz olmaları sadece bu problemde yer alan kısıtlamalardır.)
Ancak doğada Fibonacci sayılarının görüldüğü birçok örnek vardır.


Örneğin çam kozalağının saat yönünde 8 ve saatin tersi yönünde 13 spirali vardır. Ayçiçeğindeyse saat yönünde 34, saatin tersi yönündeyse 55 adet spiral bulunmaktadır.
Fibonacci Sayı Dizisi, Geometri ve Altın Oran
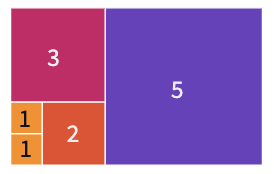
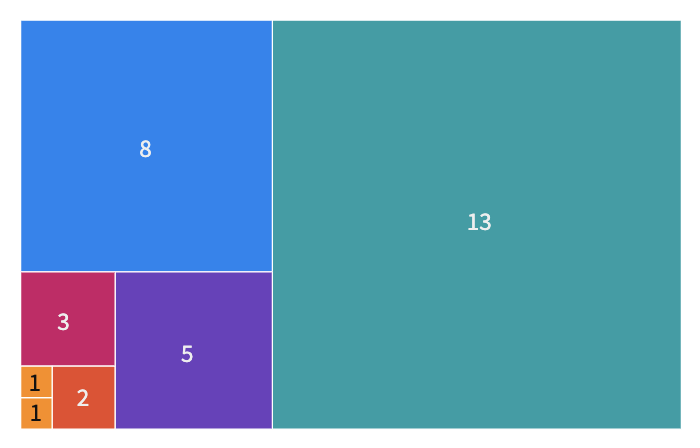
Fibonacci dizisi geometrik bir desen kullanılarak görselleştirilebilir. Kenar uzunlukları birer birim olan iki kareyi yan yana yerleştirerek başlayalım. Daha sonra sırayla kenar uzunlukları $2, 3, 5, 8…$ birim olan kareler ekleyelim. Her adımda kareler daha büyük bir dikdörtgen oluşturur. Bu dikdörtgenlerin eni ve boyu her zaman ardışık iki Fibonacci sayısıdır. Her yeni oluşan dikdörtgenin boy en oranı hesaplandığında, oranının 1,6 civarındaki belirli bir sayıya yaklaştığı görülür. İşte bu sayı ünlü altın orandır.1
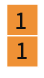
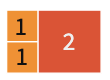
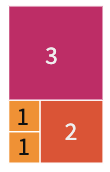

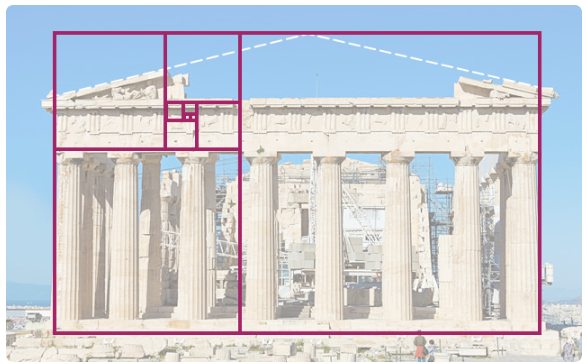
Örneğin Yunan heykeltıraş Phidias’ın Atina’daki Parthenon’u tasarlarken altın oranı kullandığı söylenmektedir. İsminin ilk harfi olan “phi”, altın oran için kullanılan semboldür.
Fibonacci Spirali ve Altın Büyüme Oranı
Fibonacci sayı dizilimine sahip ayçiçeği ve çam kozalağı merkezlerinden dışarı doğru büyür. Her yeni tohum ya da yaprak ardışık yapraklar arasındaki açıyı sabit tutarak bitkiye eklenir.
Bu sabit açının sağladığı dağılım, yaprakların en fazla miktarda güneş ışığı ve besin alabilmesi için çok önemlidir. Rasyonel sayılar hatta $\pi$ sayısı gibi irrasyonel sayılar bile çiçekler için en verimli yaprak dağılımını verememektedir. Bu açı $\frac{360^o}{\phi}$ derecedir. Bu yüzden, altın oran belki de en irrasyonel! irrasyonel sayı olarak yorumlanabilir.

Bitki ne kadar büyürse büyüsün, bu tek bir sabit dönüş açısının en uygun tasarımı üretebilmesine, 1993 yılında iki Fransız matematikçi Stéphane Douady ve Yves Couder matematiksel olarak kanıtlayana kadar şüpheyle bakılıyordu. Bitkiler ve hayvanlar kuşkusuz ki Fibonacci sayılarını birbirine bölerek altın oranı hesaplamaz, ama her zaman en verimli şekilde büyümek isterler ve bu nedenle doğa düzenli, matematiksel kalıplarla doludur.
Binet Formülü
Şu ana kadar Fibonacci sayılarını bulmak için yinelemeli formülü kullandık.
$F_1=1, $
$F_2=1, $
$F_3=F_2+F_1=1+1=2, $
$F_4=F_3+F_2=2+1=3, $
$F_5=F_4+F_3=3+2=5, …$
Peki herhangi bir Fibonacci sayısını nasıl hesaplayabiliriz? Bunun için, iki ardışık Fibonacci sayısı arasındaki -yaklaşık- altın oranı kullanabilir miyiz?
Fransız matematikçiler tarafından bulunan ve Binet formülü olarak anılan dahiyane formüle bir bakalım.
$x_1=\frac{1+\sqrt{5}}{2}$, (altın oran) ve $x_2=\frac{1-\sqrt{5}}{2}$, $x^2-x-1=0$ denkleminin kökleridir. Buna göre, herhangi bir $n$. Fibonacci sayısı $F_n=\frac{x_1^n-x_2^n}{x_1-x_2}$ şeklinde yazılabilir. Diğer bir ifadeyle $F_n=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right)$ veya $F_n=\frac{\phi^n-(1-\phi)^n}{\sqrt{5}}$.
Örneğin, yukarıdaki formülde $n=7$ için:
$$
\begin{aligned}
F_7=\frac{\phi^7-(1-\phi)^7}{\sqrt{5}} & \\
& \approx \frac{1.618034^7-(1-1.618034)^7}{\sqrt{5}} \\
& \approx 13
\end{aligned}
$$
Fibonacci Sayı Dizisi ile ilgili Etkinlikler
İnsanlık tarihinde çok uzun bir geçmişe sahip olarak en ünlü sayı dizilerinden biri haline gelen, Sanskritçeden mimariye, finanstan botanik bilimine birçok farklı alanda karşımıza çıkan bu sayı dizisi hakkında öğrencilerle birçok farklı etkinlik yapılabilir. Bu etkinlikler farklı sınıf seviyelerine göre çeşitlendirilebilir. Buradaki QR kodu okutarak tüm oyunlara dijital ortamda da ulaşabilirsiniz. (Tüm oyunlar boyunca hesap makinesi kullanılabilir.)

Fibonacci Oyunları
Oyun #1 (Bir iki, bir iki)
Domino taşları ile de oynayabileceğiniz bu oyunda, amaç her biri 1 birim eninde ve 2 birim uzunluğunda olan dikdörtgen tuğlalar kullanarak 2 birim yüksekliğinde ve 10 birim uzunluğunda bir duvarı kaç farklı şekilde inşa edebileceğimizi bulmaktır.
Öğrencilerin sistematik düşünme becerisini geliştirebilecekleri bu etkinlikle, Fibonacci sayı dizisini* keşfetmeleri sağlanabilir.
*Tuğlaların dizilimi, 1 ve 1 ile başlamak yerine 1 ve 2 ile başlamaktadır.
10 birimlik duvar, 1×2 birim ölçülerindeki tuğlaları kullanılarak 89 farklı şekilde inşa edilebilir.
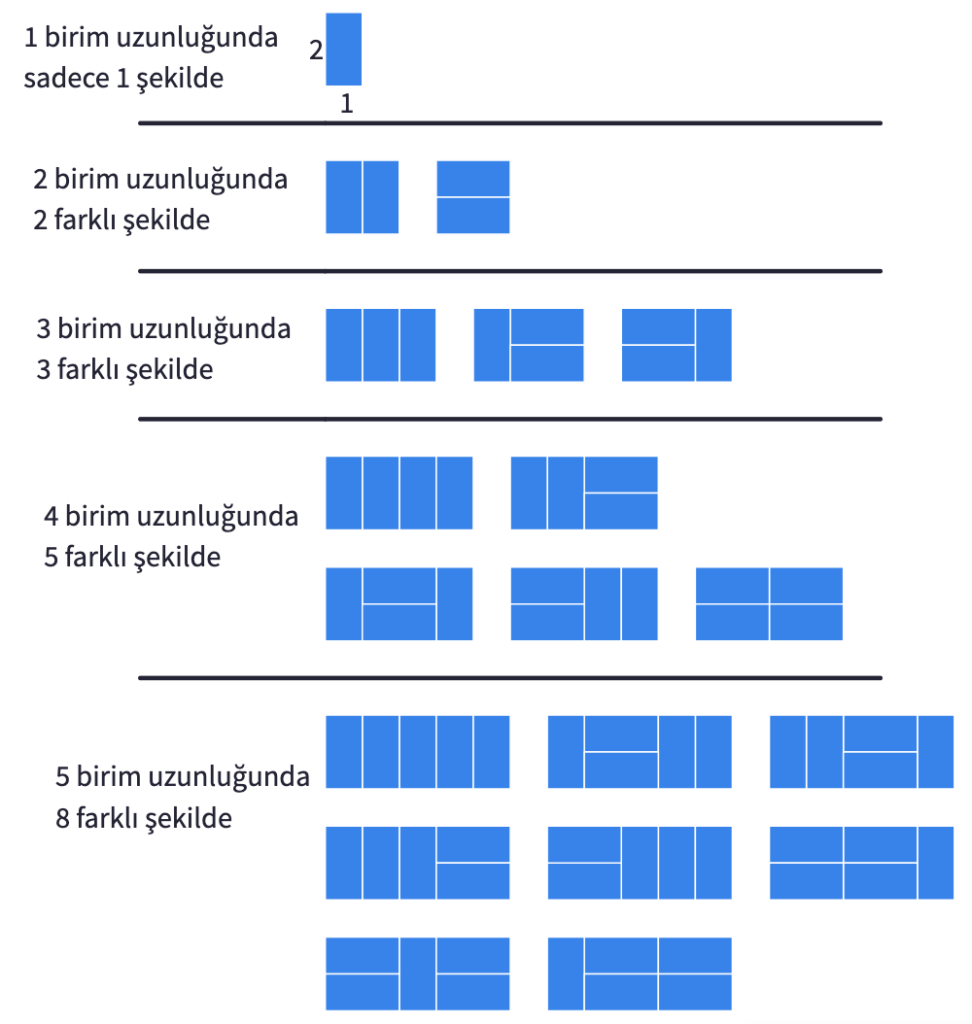
Oyun #1 Sayı Çubukları
İlk oyun 1 ve 2 numaralı sayı çubukları (ya da 1 ve 2 birim uzunlukları) kullanılarak da oynanabilir.
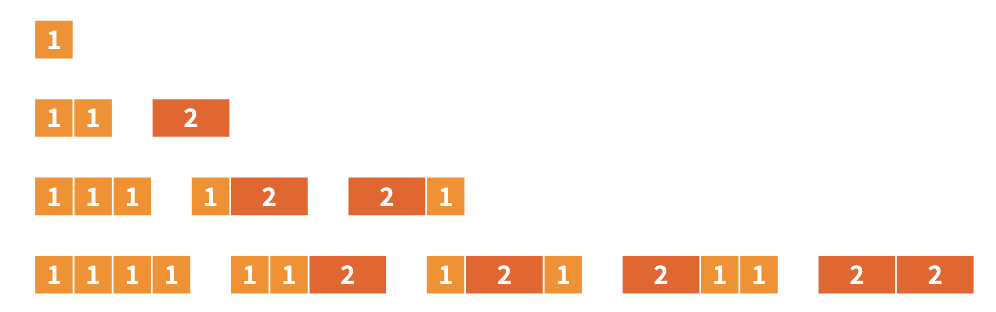
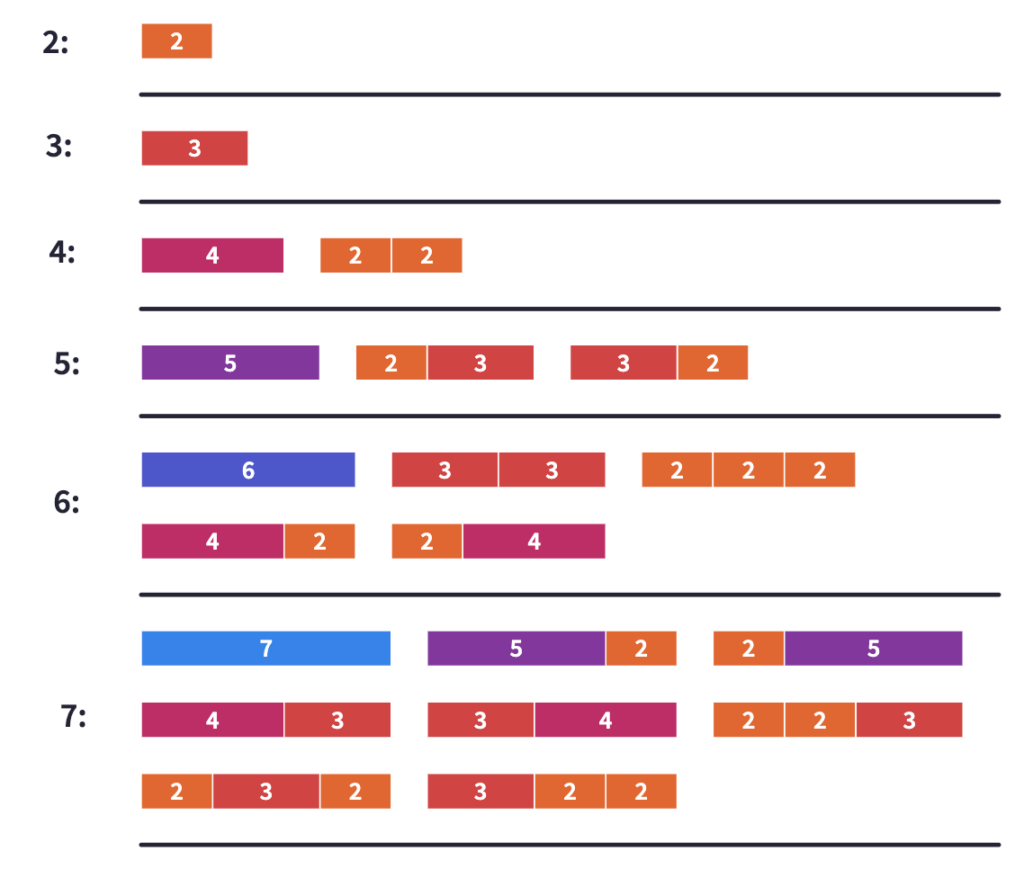
Oyun #2 (HiçBİRi yokken!)
Peki aynı oyunu hiç “1” kullanmadan, ama diğer tüm sayı çubuklarını (uzunluklarını) kullanarak oynayalım. Amaç bu sefer de 13 sayısına ulaşmak olsun.
Hiç “1” yokken, tüm sonuçlar, 1 ve 1 başlayan Fibonacci sayı dizisini verir. Öğrencilerden bu oyunlar sırasında, çalışmalarını kaydetmek için tablo kullanmalarını isteyebilirsiniz.

Oyun #3 (TEKer TEKer)
Bu sefer elimizde sadece 1, 3, 5, 7 sayı çubukları (uzunlukları) var. (Örneğin 4 sayısını [4 birim uzunluğunu] üç farklı yolla oluşturabiliriz; “1111”, “13” ve “31”.)
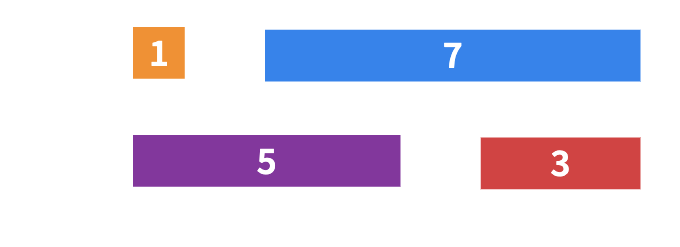
Öğrencilerden yalnızca bu tek uzunluktaki çubukları kullanarak 5, 6, 7 sayılarını (uzunluklarını) oluşturmalarını isteyebilirsiniz.
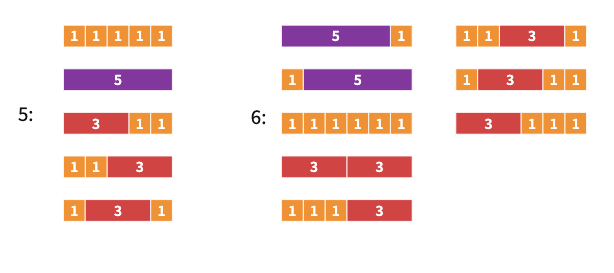
Oyun #5 (Adım adım)
İlk oyunun bir başka versiyonu da merdiven çıkmak üzerinedir. Örneğin bir merdiveni çıkarken ya her adımda bir basamak ya da her adımda iki basamak çıkabilelim. Bu şekilde, merdivenden yukarıya kaç farklı şekilde çıkabileceğimize dair bir oyun oynanabilir.
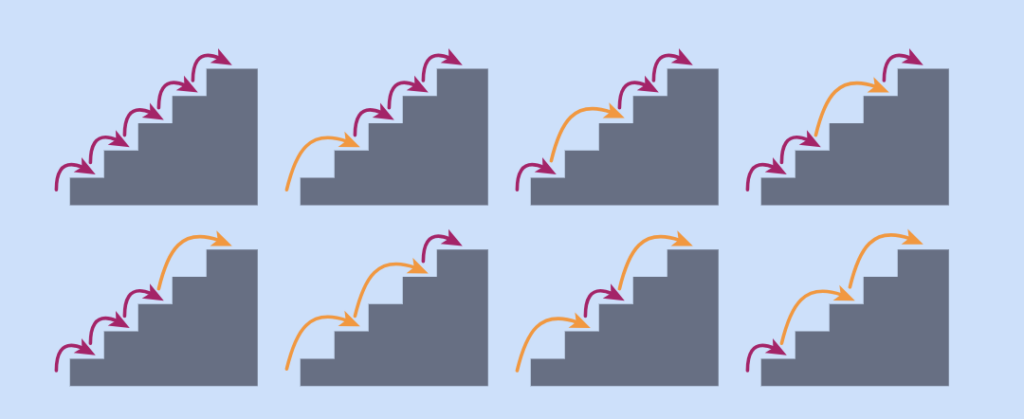
Örneğin, 5 basamağı 8 farklı şekilde çıkabiliriz. 6, 7 ve 8 basamaklı merdivenler için kaç farklı yol vardır?
Olanak varsa, öğrencilerin gruplar halinde çalışıp, merdivenlerde deneyerek, farklı çıkış biçimlerini kaydetmelerini ve böylece Fibonacci sayı dizisini keşfetmelerini sağlayabiliriz.
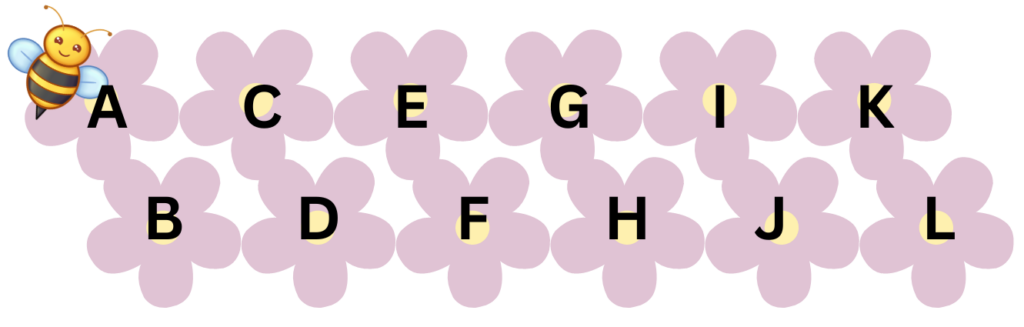
Oyun #8 (Hep ileri)
Bir çiçek bahçesine düşen sol üst köşedeki arı hep ileri uçarak (örneğin D çiçeğinden A, B ve C çiçeklerine gidemez, ama E ve F çiçeklerine uçabilir) ve her adımda bir çiçek ilerleyerek kaç farklı yolla E çiçeğine ulaşabilir? Peki ya L çiçeğine?
Oyun #13 (Fibonacci Sürprizleri)
Artık Fibonacci sayılarına aşina olan öğrencilere şu soruları sorabilirsiniz.
$\bullet$ Hangi Fibonacci sayıları çifttir? Bunun nedenini açıklayabilir misiniz?
$\bullet$ Hangi Fibonacci sayıları 3’e bölünebilir (veya 4’e bölünebilir)?
Öğrenciler, sayıları bölünebilme kuralları ile test ettiklerinde, dizideki her üçüncü sayının (2’den başlayarak) 2’nin katı, her dördüncü sayının (3’ten başlayarak) 3’ün katı ve her beşinci sayının (5’ten başlayarak) 5’in katı olduğunu göreceklerdir.
$$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…$$
Fibonacci sayılarıyla ilgili birçok özellik vardır. Öğrencilere, aşağıdaki soruları da yönelterek farklı grupların farklı Fibonacci sürprizlerini keşfedip, birbirleri ile paylaşabilecekleri bir oyun oynanabilir.
$\bullet$ Ardışık üç Fibonacci sayısını toplarsanız ne olur? Bunun nedenini açıklayabilir misiniz?
$\bullet$ Her ardışık dört Fibonacci sayısının toplamının aynı zamanda ardışık iki Fibonacci sayısının toplamına eşit olduğunu gösterin.
$\bullet$ Herhangi ardışık dört Fibonacci sayı grubunun, ilk ve sonuncu sayılarını toplayıp ikiye böldüğünüzde ne olur?
$\bullet$ Herhangi ardışık beş Fibonacci sayı grubunun, ilk ve sonuncu sayılarını toplayıp üçe böldüğünüzde ne olur?
$\bullet$ Herhangi ardışık dokuz Fibonacci sayı grubunun, ilk ve sonuncu sayılarını toplayıp yediye böldüğünüzde ne olur?
$\bullet$ Bu genellemeleri çoğaltabilir misiniz?
Oyun #21 (Fibonacci ve Lucas)
Bazı kaynaklara göre Fibonacci dizisi 0 ve 1 ile başlar, fakat bu dizinin benzersiz özelliklerini çok da fazla etkilemez. Peki tamamen farklı iki sayı ile diziye başlarsak ne olur?
Öğrencilerden herhangi iki tamsayıyı seçerek kendi Fibonacci dizilerini oluşturmalarını isteyebilirsiniz. Hatta bu dizilere onların adını vererek, öğrenciler için bu aktiviteyi daha da kişiselleştirebilirsiniz. Öğrencilerden gelen sayı dizilerini bir yerde toplayarak, onlara neler fark edip neler merak ettiklerini soralım. (Öğrencilerden negatif sayılar kullanarak diziye başlayanlar olabilir, onları da iki sonraki oyun için kayıt altına almayı unutmayalım.) Örneğin,

Örneğin, 1, 1,… yerine 2, 1,… ile başlarsak Lucas dizisi adı verilen bir dizi elde ederiz.
$$2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, …$$
Lucas dizisi de Fibonacci dizisi gibi her terimin önceki iki terimin toplamı olduğu aynı rekürsif kurala göre ilerler. Peki bu iki dizinin başka ortak yönleri var mıdır? Ya da öğrencilerin yazdıkları tüm dizilerin? Hesap makinesi yardımıyla öğrencilerden kendi dizileri ve Lucas dizisi için ardışık terimlerin oranlarını bulmalarını isteyebilirsiniz.
Aynı Fibonacci sayı dizisinde olduğu gibi, ardışık iki Lucas sayısı arasındaki oran da öğrencilerin aynı rekürsif kuralı kullanarak yazdıkları tüm diziler için hesapladıkları oran da altın orana yakınsar!
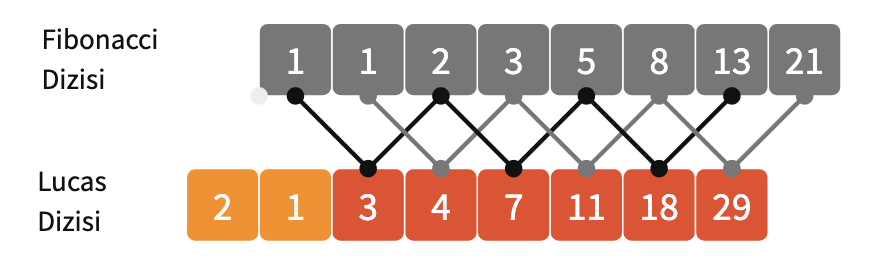
Peki Fibonacci sayılarını kullanarak Lucas sayılarını nasıl elde edebiliriz?
Fibonacci dizisinde, bir terim atlayarak sayıları topladığımızda, üçüncü terimden başlayarak Lucas sayılarını elde edebiliriz.
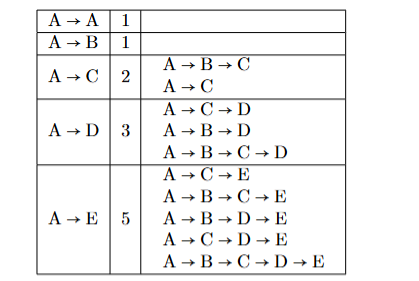
Oyun #34 (Cebirsel Fibonacci)
(Bu oyundan başlayarak sıralanan oyunlar yedici sınıf ve üzeri öğrencilere önerilir.)
Hangi sayıdan başlarsak başlayalım iki ardışık terimin arasındaki oranın her zaman altın orana yaklaşması özelliğini araştıralım. (Cebir bilen öğrenciler çoktan, her bir terimi cebirsel ifade olarak yazarak genellemeler yapmaya başlamış olabilirler.)
Öğrencilerden ilk terimi $x$, ikinci terimi $y$ olan ($x\neq 0$, $y\neq 0$ ) ve Fibonacci sayı dizisinin kuralı ile ilerleyen diziyi oluşturmalarını isteyelim.

Her bir terimi oluşturan cebirsel ifadelerin katsayıları nasıl ilerliyor?
$\bullet$ İlk terimi 5, beşinci terimi 34 olan ve Fibonacci kuralı ile ilerleyen diziyi oluşturalım.
$x=5$ olduğunda, $34=2x+3y$’dir. Bu durumda, diziyi $5, 8, 13, 21, 34, 55, …$ şeklinde yazabiliriz.
$\bullet$ Üçüncü terimi 22 ve altıncı terimi 90 olan diziyi oluşturalım.
$x+y=22$ ve $3x+5y=90$ denklem sistemi çözüldüğünde, diziyi $10, 12, 22, 34, 56, 90, 146, …$ şeklinde yazabiliriz.
Öğrencilerden kendi sorularını oluşturup, birbirleri ile değiştirerek bilinmeyen sayıları bulmalarını isteyebilirsiniz.
Oyun #55 (Negatif düşünceler)
Fibonacci dizisi bazı kaynaklara göre 1 ve 1 ile başlarken, bazı kaynaklara göreyse 0 ve 1 ile başladığını söylemiştik. Peki ya sıfırdan öncesi? Öğrencilere Fibonacci dizisini negatif yönde nasıl kurgulayabiliriz diye soralım.
$$0, 1, 1, 2, 3, 5, 8, 13, 21, …$$
$F_0=0$ ise $F_{-1}$’in ne olması gerekir? $F_{-2}$? $F_{-3}$?
$$-21, 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, …$$
Öğrencilere, sürekli işaret değiştirerek, aynı sayı değerleriyle negatif yönde ilerleyen bu sayıları nasıl bulabileceğimizi sorabilirsiniz.
$$F_{-n}= (-1)^{n-1}\cdot F_n$$
Örneğin,
\begin{align} &\bullet \quad F_{-1}= (-1)^{1-1} \cdot F_1=1 \ &\bullet \quad F_{-2}= (-1)^{2-1} \cdot F_2= -1 \ &\bullet \quad F_{-3}= (-1)^{3-1} \cdot F_3=2 \end{align}
Oyun #89 (Sihirli Toplam)
Öğrencilereden herhangi iki sayıyla başlayıp, Fibonacci kuralını kullanarak bir dizinin ilk on sayısını yazmalarını isteyin (ilk iki sayıyı 10’dan küçük seçmeleri, dizinin diğer sayılarını yazarken kolaylık sağlayabilir). Bu on sayılık dizinin sayılarının toplamı, yedinci sayının 11 katıdır. Toplamı hemen söyleyip, bu numarayı nasıl yaptığınızı öğrencilere sorabilirsiniz.
İpuçları:
Öğrencilerden ilk $n$ Fibonacci sayısının toplamını bulmak için bir model geliştirmelerini isteyelim. Öğrencilerden yine sistematik düşenerek çalışmalarını kaydetmelerini isteyebilirsiniz.
Örneğin ilk 5 Fibonacci sayısının toplamı $1+1+2+3+5=12$’dir.
İlk 8 Fibonacci Sayısının toplamıysa $1+1+2+3+5+8+13+21=54$’tür.
Sonuç her zaman iki sonraki Fibonacci sayısının 1 eksiğidir.
Öğrencilerden herhangi iki sayıyla başladığımızda toplam formülünü bulmalarını da isteyebilirsiniz.
Bu formül, $F_1+F_2+F_3+…+F_n=F_{n+2}-F_2$’dir.
Bu aşamadan sonra başta yapılan numarayı nasıl yaptığınızı bulmaları daha kolay olacaktır.
Oyun#144 (Bir ileri bir geri)
Son olarak ögrencilerden $F_{n+1}$ ve $F_{n-1}$ Fibonacci sayılarınının çarpımı hakkında bir model geliştirmelerini isteyelim.
Öğrenciler buradaki gibi örnekleri çoğaltarak, $F_{n-1}$. $F_{n+1}=\left(F_n\right)^2+(-1)^n$ olduğunu formülleştirebilirler.
$$
\begin{array}{ll}
n=2 \text { için, } F_1 \cdot F_3=2 & =\left(F_2\right)^2+1 \\
n=3 \text { için, } F_2 \cdot F_4=3 & =\left(F_3\right)^2-1 \\
n=4 \text { için, } F_3 \cdot F_5=10 & =\left(F_4\right)^2+1 \\
n=5 \text { için, } F_4 \cdot F_6=24 & =\left(F_5\right)^2-1
\end{array}
$$
Bu ve bunun gibi oyunlarda keşfettiğimiz birçok sonuç, çok bilinen Fibonacci dizisinin az bilinen şaşırtıcı! ve güzel sayısız özelliklerinden bazılarıdır. Tüm bu özellikler ve daha niceleri üzerine araştırma yapan ve sadece Fibonacci sayılarına adanmış bir dernek bile vardır!
Pi Günü kadar ünlü olmasa da Fibonacci Günü her yıl 23 Kasım’da kutlanır çünkü tarih (11/23) ay/gün formatında yazıldığnda bir Fibonacci sayı dizisi oluşturur. 2058 yılındaki kutlamalarda görüşmek üzere…
Kaynaklar
[1] K. Dexlin Finding Fibonacci: The Ruestte Rediscover the Forgotten Mathematical Genius, Who Changed the World, Princeton University Press 2017.
[2] Knott, R. (2013, November 4). The life and numbers of Fibonacci. Plus Maths.
https://plus.maths.org/content/life-and-numbersfibonacci ve https://r-knott.surrey.ac.uk/Fibonacci/fibpuzzles.html
[3] Legner, P. Sequences and Patterns: Fibonacci Numbers. Mathigon https://mathigon.org/course/sequences/fibonacci
[4] Stone, A. (2024, January 4). The astonishing behavior of recursive sequences. Quanta Magazine. https://www.quantamagazine.org/the-astonishing-behavior-of-recursive-sequences
- Altın oran, $\phi=1,61803398875…$ değerine sahip bir irrasyonel sayıdır. Ardışık iki Fibonacci sayısını birbirlerine bölerek yaklaşık olarak hesaplanabilir. Bir diğer ifadesi de $\frac{1+\sqrt{5}}{2}$ şeklindedir. ↩︎

