Yazar: Ali Nesin – Nesin Matematik Köyü – anesin@matematikkoyu.org
Yıl: 2024-1
Sayı: 119
1. Biraz Tarih Öncesi
Sayıların bulunması kolay olmamıştır kuşkusuz. Bulunan ilk nicelik kavramları ”az” ve ”çok” olmalı. Daha sonra ”iki”yi bulmuş olmalılar. ”Bir” sayısı, ”iki” bulunduktan sonra bulunabilir ancak. ”İki” bulunmamışsa ”bir”in gerekliliği kavranamaz.
Yazının daha bulunmadığı eski çağlara geri dönüp insanlık tarihinde sayıların nasıl bulunduğunu, sayı saymanın hangi evrelerden geçtiğini bilemeyiz. O günlerden bugüne bir ipucu kalmasına olanak yoktur. Ama yakın geçmişte gözlenebilen ilkel kabilelerin sayı kavramları incelenebilir. Yani, tarih yerine etnografyaya kayılabilir.
Çocuklarını sayabilen, ancak başka hiçbir şeylerini sayamayan ilkel kabilelere rastlanmıştır. Genelde ancak üçe kadar sayabilen Avustralyalı bir kabilenin yerlileri dokuz çocuğa kadar sayabiliyorlardı. Şu yöntemi kullanıyorlardı: her aile ilk çocuğuna hep aynı adı veriyordu. İkinci, üçüncü çocuklarına da… Böylece, akşam toplanıldığında, anababa çocuklarını ”saymadan” hepsinin orada olup olmadığını anlayabiliyordu.
Kendi dillerinde ancak dörde kadar sayabilen Paraguay’da yaşayan bir kabileye, İspanyol işgalciler İspanyolca saymasını öğretmişler. Ancak ezbere sayabilen yerliler nesneleri sayarken o denli yanılıyorlarmış ki saymanın ne demek olduğunu bildikleri pek söylenemezmiş. Daha da ilginci, bu kabilenin üyeleri, beşe kadar bile saymayı beceremezken, sürülerinde bir hayvan kaybolduğunu anlayabiliyorlarmış.
Buna benzer ilginç örnekler çoktur. Örneğin, her türlü nesneyi en az ona kadar sayabilen, ancak bu sayma eylemini saydığı nesnelere dokunmadan yapamayan kabileler de vardır. Ya sayarken bir yandan da vücudunun çeşitli yerlerine dokunmak zorunluluğunu duyan kabilelere ne denir? Ona kadar saymak için, genellikle sol elin baş parmağından başlayarak sağ elin küçük parmağına kadar birer birer dokunurlar. Ondan büyük sayılar için ayak parmakları kullanılır. Bu kabilelerden daha da ilkelleri ilk beş sayıdan sonra bileklerine, dirseklerine, omuzlarına dokunurlar. ”Çok sayısı” için saçlarını gösteren kabileler de biliniyor.
Altıdan yukarı sayamayan aritmetiği zayıf bir başka kabileye reisliğe en fazla hayvanı olan kişiyi getirirlermiş. Hayvanları nasıl sayarlardı diye merak ediyor insan. Kimin daha fazla hayvanı olduğunu bulmak için saymaya gerek yoktur ki! Hayvanları karşılaştırmak yeterlidir. İki adayın hayvanları yan yana iki ağıla konur, sonra ağıllardan hayvanlar birer birer çıkarılır. Ağılı ilk boşalan seçimi kaybeder.
Bir başka kabilenin üyeleri, ancak ”bir, iki, çok” diye sayabilirken, tek sayıları çift sayılardan ayırt edebiliyormuş. Sabah, çoban koyunlarını ağıldan ikişer ikişer çıkarırmış. En sona bir koyun kalırsa tek sayıda koyuna, iki koyun kalırsa çift sayıda koyuna sahip olduğunu anlarmış. Akşam koyunları ağıla gene aynı yöntemle sokarmış. Örneğin sabah çift sayıda koyunla evden çıkıp akşama tek sayıda koyunla eve dönerse koyunlarının kaybolduğunu anlarmış. Bu yöntemle, sürüden çift sayıda koyunun eksildiği anlaşılamaz elbet.
Bu örneklerden şu çıkıyor: Sayıları nesnelerden soyutlamak pek kolay olmamıştır. ”Bir elma, iki elma”dan, ”bir, iki”ye geçiş küçümsenmeyecek bir soyutlama gücü gerektirir.
2. Biraz Metafizik
Bu kadar tarih yeter, biraz da konunun felsefesine eğilelim. Yazının başlığı üzerine düşünelim. Hatta daha genel olarak ”$x$ nedir?” türünden sorular üzerine düşünelim. Örneğin okurların daha çok ilgilendiğini sandığım ”sanat nedir?” ”demokrasi nedir?” gibi sorular üzerine… Hatta ”elma nedir?” sorusu üzerine…
”$X$ nedir?” sorusu sorulduğunda, bizim dışımızda, bizden bağımsız bir $X$’in olduğunu varsayıp, o bizden bağımsız olan $X$’i anlayıp kavrayıp tanımlayabileceğimizi varsayarız. Bu varsayım en az iki sorun içerir: 1) Bizden bağımsız bir $X$ var mıdır? 2) Eğer varsa bizden bağımsız olan bu $X$’i tanımlayabilecek kadar anlayabilir miyiz?
Aslında ”var olmak”ın anlamından başlamalıyız düşünmeye… İstesek de istemesek de bu soru üzerine de düşüneceğiz.
Birinci sorudan başlayalım: Bizden bağımsız bir $x$ var mıdır? ”Elma” var mıdır örneğin? Yoktur elbet! Her biri birbirinden değişik ve her an değişen ”elmamsı” nesneler belki vardır; ama ”Elma” diye büyük e’yle yazılan tekil bir şey yoktur. Dolayısıyla ”elma”nın tam bir tanımı yapılamaz… Olsa olsa, varolan tüm ”elma”ların (elmamsıların) ortak özelliklerinden bazılarını sıralayabiliriz, ki o zaman da ”elma”yı tanımlamış olmayız, sadece elmamsıların ortak birkaç özelliğini sıralamış oluruz. Gerçekte olmayan elmanın nesi tanımlanabilir ki!
Ama diyelim ki elma diye bizim dışımızda bir nesne var. İkinci soruya geçelim: Eğer bizden bağımsız bir $X$ varsa, o $X$’i tanımlayabilecek kadar anlayabilir miyiz? Cins cins elma olduğundan ve her cinsten birden çok elma olduğundan ve her cinsten her elmanın yetişme koşulları değişik olduğundan ve her elma her an değiştiğinden ve her elma içinde geleceğini de barındırdığından, sonlu sayıda gözlemle, sınırlı algılama yetilerimizle, sonlu sayıdaki sözcük dağarcığımızla ve sonlu sayıda tümceyle elmayı tanımlayamayız. Elimde güç olsa, sözgelimi bir tanrı olsam (haşa!), verebileceğimiz tüm elma tanımlarına uyan, ama elma olmayan bir nesne yaratabilirim.
”Sanat, felsefe, sosyalizm ya da demokrasi nedir?” gibi daha kavramsal sorulara gelince… Önce şunu söylemek gerekir: Bu sorular birkaç türlü algılanabilir. Örneğin şöyle: a) Belli bir tarih ve coğrafyada $X$ nedir? b) Bugün $X$ ne olmalı? c) Benim $X$ anlayışım nedir? Her soru türünün ayrı bir yanıtı olmalı. Bu ayrıntıları yok sayıp olabildiğince anlaşılır ve açık seçik bir soru sorulduğunu varsayalım.
Bu gibi daha soyut kavramlar söz konusu olduğunda tanıma biraz daha yaklaşılabileceğini düşünüyorum. Fiziksel bir varlık olduğunu düşündüğümüz elmanın tanımı imkânsız, öte yandan bir kavram olan demokrasinin tanımı neredeyse mümkün. Örneğin biçimsel demokrasi tanımlanabilir; on sekiz yaşını bitirmiş herkes oy verebilir ve herkesin oyu bir sayılır gibi maddelerle… Güçlerin ayrılığı, azınlık hakları gibi bazı konularda kimileyin muğlak kalınsa da gerçek bir tanıma yaklaşmak çok daha olası görünüyor.
Sevgi, aşk, arkadaşlık, dostluk, kahramanlık gibi kişiden kişiye değişmek zorunda olan kavramları hariç tutarsak, toplumsal kavramlar fiziksel varlıklardan genellikle daha çok tanıma elverişlidirler; çünkü daha zihinseldirler, daha soyutturlar ve durmadan değişmezler.
Kavramlar daha çok bizim malımızdır. Ne de olsa o kavramları zekâmız ve anlağımızla biz yaratmışızdır, biz bulmuşuzdur, biz dile getirmişizdir.
Sonuç olarak, bizim dışımızda olan, yani salt zihinsel olmayan herhangi bir şeyin, tam matematiksel olmasa bile, matematiğe yakın bir tanımını vermek zordan öte imkânsızdır. Öte yandan soyut kavramların tanımı daha kolay verilebilir. Birazdan bunun çok somut bir örneğini göreceğiz.
”Sayı”yı bizim dışımızda bir şey olarak görebilir miyiz? Örneğin bizim dışımızda ”bir” var mıdır? Biraz önce elmanın olmadığını söylerken aslında asıl söylemek istediğim ”bir”in olmadığıydı. Elmanın olmaması ”bir elma”nın olmaması demektir, yani ”bir”in olmaması…
”Bir elma” yok dedik; ama gene de ”başıma bir elma düştü” tümcesine bir anlam verebiliyoruz. Birine, ”bana mutfaktan bir elma getir” diye seslendiğimizde, o kişi ne demek istediğimizi anlayıp bize bir elma getirebiliyor. Demek ki ”bir elma” olmasa da ”bir elma”nın anlamı var. İlginç bir durum…
Sanırım ”bir elma”dan çok, elle tutulamayan, gözle görülemeyen, sadece tezahürü fark edilen, belki de beynimizin -yaşam boyu gördüğümüz tek tek elmalardan- yarattığı soyut ve salt zihinsel, ama bir türlü kâğıda geçiremediğimiz, simgelerimize ve ele avuca sığmayan bir ”elma” düşüncesi vardır. Her ”gerçek elma”, elma düşüncesini oluşturan şeylerden biridir.
Matematik, bizim dışımızda ve bizden bağımsız var olan karmaşık ve anlaşılmaz evreni basitleştirerek ve tamamıyla zihinsel bir biçimde ve simgelerle açıklamaya çalışan bir uğraş dalıdır.
Bizim dışımızda var olan evren tüm boyutlarıyla anlaşılamaz. O evreni anlayabilmek için basitleştirmek, yani yalan söylemek zorundayız. Anladığımız evrenle ilgili bilgileri ayrıca birbirimize de aktarmak zorundayız. Dolayısıyla anladığımızı ve algılayabildiğimizi basitleştirerek simgeleştirmeliyiz (yeni bir dil yaratmalıyız) ve kâğıda dökmeliyiz. Başka çözüm yolu yoktur.
Hata iki yerde belirir: 1) Eksik algılarız, 2) Algıladığımızı kâğıda eksik geçiririz.
Matematik ya da matematiksel yöntemler, evreni (aşağı yukarı) anlamak için tek yoldur. Başka bir yol yoktur ve olamaz.
”Bir” kavramı da somut dünyayı anlamak için soyut matematiğin bulduğu kavramlardan biridir. Matematiksel anlamda kullanılan ”bir”i tanımlayabiliriz, tanımlayacağız da. Öte yandan somut dünyada ”bir”i tanımlamak olanaksızdır. Bu yüzden vereceğimiz matematiksel ”bir” kavramı okurun algıladığı ”bir”den değişik olacaktır.
”Bir”i dış dünyadan koparıp soyut bir kavram olarak ve tamamıyla zihinsel bir biçimde tanımlayacağız.
3. Sayı Neye Yarar?
Sayı yaşamda iki işe yarar: 1) Nesneleri, şeyleri saymaya (cebir, aritmetik, muhasebe), 2) Uzaklıkları ölçmeye (geometri). Birinci yaklaşıma yukarıda değindik ve bu yaklaşımın doğurduğu felsefi sorunları gördük. İkinci yaklaşım da aslında birincisinden pek farklı değildir: Mesafe ölçmek, özünde, iki nokta arasındaki ”bir metre”leri ölçmektir. Ama bu ikinci yaklaşım sayı kavramına geometrik bir sezgi sağlar. Bu yaklaşım sayesinde, sayıları bir doğru üstündeki noktalar olarak gösterebilmemiz gerektiğini anlarız:
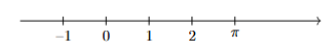
Ne yazık ki bu yaklaşımı da matematikselleştiremeyiz. Her şeyden önce doğruyu tanımlamamız gerekiyor, sonra doğru üstündeki noktayı, sonra ”eşit mesafe”yi… Çok eski Yunan matematiğinde bu yaklaşım söz konusuydu; önce geometrik doğru tanımlanır, geometrik doğru kavramından sayı kavramına geçilirdi. Ama çağdaş matematikte tam tersi yapılır, önce sayı tanımlanır, sonra doğru.
4. Sayı Türleri
Anlayamadığımız ve hiçbir zaman anlayamayacağımız ve belki de olmayan ”bir”i basitleştirerek matematikselleştireceğim. Daha doğrusu, ”bir” adını vereceğim yepyeni bir nesne yaratacağım. Ama önce sayının tanımını vermeliyim…
Ne yazık ki sayının tanımı yoktur! Biz ne istersek sayı o olur. Aynen demokrasi kavramı gibi… Elbette $1, 2, -1, 0, \sqrt{2}, \pi, \pi^2, \pi – 3\sqrt{2}$ birer sayı olmalı. Ama bunların dışında?
Matematikte ”sayı” diye genel geçer bir kavram yoktur. Doğal sayılar, tamsayılar, kesirli sayılar, cebirsel sayılar, gerçel sayılar, karmaşık (kompleks) sayılar, Hamiltonlar, oktonyonlar, ordinaller, kardinaller, sonsuz küçük sayılar şimdi aklıma gelen çeşitli sayı türleridir ama matematikte genel bir sayı kavramı yoktur. Ya da şöyle söyleyeyim: Genel olarak, sayı denildiğinde yukarıda sıraladığım sayı türlerinden biri anlaşılır. Ama hiçbir saygıdeğer matematik kitabında genel bir ”sayı” tanımı bulamazsınız.
Belki tek bir istisnayla… Birkaç yıl önce, İngiliz matematikçi John Conway’in oyunlar kuramında kendi geliştirdiği bir yöntem sayesinde bulduğu ”sayı” tanımı, biraz önce sıraladığım Hamiltonlar ve oktonyonlar dışında tüm sayı türlerini kapsar. John Conway’in sayılarına sürreel/gerçelötesi sayılar denir. Eğitimli ya da değil, matematik kafası olan herkesin bu olağanüstü buluşu anlayabileceğini düşünüyorum.
Aşağıda birkaç tür matematiksel sayı kavramı üzerinde duracağım.
5. Doğal Sayılar
Doğal sayılardan başlayalım. En çok bildiğimiz, öğrendiğimiz ilk sayılardır bunlar.
Belli ki doğal sayıları saymak için kullanıyoruz: Sıfır, bir, iki, üç…
Doğal sayılar sıfattır. ”Beş elma”da olduğu gibi. Sayıları günlük yaşamda sıfat olarak kullanırız. Ama matematikte öyle olmayacak. Matematikte her doğal sayı bir nesne olacak.
Sıfırdan başlayalım. Sıfırı boş küme olarak tanımlıyorum:
$$0 = \emptyset.$$
”Sıfır nedir?” diye soracak olursanız, ”sıfır boş kümedir” derim. Hiçbir kuşkuya yer vermeyecek kadar açık bir tanım… Neredeyse… ”Boş küme”nin tanımını bilirsek sıfırın da tanımını biliriz.
Boş kümenin tanımını vereyim: Boş küme, hiç öğesi olmayan bir kümedir.
Öğe ve küme kavramlarını bilmemiz gerekiyor şimdi de…
Hiçbir şey bilmeden yeni bir şey bilmenin imkânı yoktur. Yoktan yeni bir şey var edilemeyeceğinden… ”küme” ve ”öğe” kavramlarını tanımlamadan kabul edeceğiz.
Görüldüğü gibi matematiksel sıfır matematiksel bir nesnedir (bir kümedir, boş kümedir), sıfat değildir.
Şimdi sıra ”bir”i tanımlamaya geldi. Biri şöyle tanımlayacağım:
$$1 = {0}.$$
Yani ”bir”, sıfırdan oluşan kümedir. Bir kümesinin bir tek öğesi vardır, o da sıfırdır. ”Gerçek bir”le hiç mi hiç ilgisi yok… Zaten ”gerçek bir”in varlığı bile kuşkulu…
Doğal sayıları tanımlamaya devam ediyorum:
$2 = \{0, 1\}$
$3 = \{0, 1, 2\}$
$4 = \{0, 1, 2, 3\}$
$5 = \{0, 1, 2, 3, 4\}$
Yöntem anlaşılmıştır sanırım. Her doğal sayı, kendisinden önce gelen doğal sayıların kümesi olarak tanımlanır.
Doğal sayılar kümesi $\mathbb N$ olarak simgelenir. Yani,
$$\mathbb N = {0, 1, 2, 3, 4, 5, …}.$$
Doğal sayılar kümesinde toplama ve çarpma diye iki işlem tanımlanır. Bu işlemlerin matematiksel tanımını burada vermeyeceğim, ama -bana inanın– toplama işlemi $5 + 6 = 11$ olacak biçimde, çarpma işlemi de $5 \times 6 = 30$ olacak biçimde ”gerçeğe” sadık kalarak, tanımlanmıştır.
6. Tamsayılar
Doğal sayılarda toplama yapabiliriz, ama çıkarma yapamayız, örneğin 3’ten 5’i çıkaramayız; $-2$ yok $\mathbb N$ kümesinde çünkü. Çıkarma yapabilmek için doğal sayılar kümesini tamsayılar kümesine genişletmeliyiz.
Tamsayının matematiksel tanımını vermeyeceğim, bu ortamda gerekmez. Ama en azından şunu söyleyeyim, her tamsayı bir küme olarak tanımlanır. Örneğin $-1$ bir kümedir, $-2$ de bir kümedir.
Tamsayılar kümesi $\mathbb Z$ olarak simgelenir:
$$\mathbb Z = { …, -3, -2, -1, 0, 1, 2, 3,… }.$$
Tamsayılar kümesinde toplama, çarpma ve çıkarma yapabiliriz. Bu üç işlemin matematiksel birer tanımı vardır. Gene ”gerçeğe” uygun bir biçimde tanımlanmıştır işlemler. Örneğin çarpma işlemi $(-5) \times (-6) = 30$ olacak biçimde tanımlanır.
7. Kesirli Sayılar
Tamsayılar kümesinde toplama, çarpma ve çıkarma yapabiliriz, ama bölme yapamayız. Örneğin 2’yi 4’e bölemeyiz; çünkü $1/2$ sayısı tamsayı değil. Bölme yapabilmek için tamsayılar kümesini kesirli sayılar kümesine genişletmeliyiz.
Gene her kesirli sayı bir küme olarak tanımlanmıştır. Matematikte her şey kümedir (hemen hemen).
Kesirli sayılar kümesi $\mathbb Q$ olarak gösterilir:
$$\mathbb Q = {a/b : a, b \in Z \text{ ve } b \not = 0}.$$
Kesirli sayılarda toplama, çıkarma, çarpma ve bölme işlemlerinin tanımları vardır(Sadece sıfıra bölünmez.) ve bu tanımlar ilkokulda öğrendiğimiz işlemlerle uyum içindedir.
8. Gerçel Sayılar
Kesirli sayılarda istediğimiz hemen hemen tüm cebirsel işlemleri(Ama kök alamayız, örneğin $\sqrt{2}$ sayısı kesirli bir sayı değildir.) yapabiliriz.
Eski Yunanlılar, özellikle Pisagorcular, çok uzun bir süre tüm ”sayı”ların(Daha doğrusu mesafelerin.) kesirli olduklarını sanmışlardır. Günün birinde $\sqrt{2}$’nin(Yani kenarları 1 uzunluğunda olan bir karenin köşegeninin uzunluğunun.) kesirli olmadığını keşfettiklerinde büyük bir düşkırıklığına uğramışlar. Felsefelerine de ters düşen bu bilgiyi birkaç yüzyıl saklamışlar; ama bir gün –başka ne yapsınlar ki? ne yapabilirler ki?- gerçeği kabullenmek zorunda kalmışlar.
Yüzyıllar sonra $\pi$ sayısının da kesirli olmadığı anlaşılmış; o kadar eski değil, aşağı yukarı 150 yıl önce.
$\pi$ sayısı $3,14159\ldots$ diye sonsuza kadar, kendini hiç tekrar etmeden gider. Sadece $3,14$ olsa kesirli olacak çünkü $3,14 = 314/100$.
Kesirli sayılar kümesinde ”delik” vardır… Örneğin $\sqrt{2}$’nin olduğu nokta yoktur! Bir başka örnek vereyim: $0,1$ kesirli sayıdır. $0,12$ de kesirlidir. $0,123$ de… $0,1234567891011121314$ de… Ama bu diziyi sonsuza kadar sürdürecek olursak, elde edeceğimiz,
[0,1234567891011121314\ldots(Sonsuza kadar yazmak için yeterince yerim ve zamanım yok.)]
”sayısı” kesirli bir sayı değildir.
Kesirli sayıların bu tür ”delik”lerini kapatan sayılara gerçel sayılar denir. $\sqrt{2}$ de kesirli olmayan gerçel sayılardandır, $\pi$ sayısı da. Hatta $\pi^2$ de kesirli olmayan gerçel bir sayıdır.
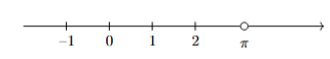
Öbür sayılarda da olduğu gibi, her gerçel sayı bir kümedir… Gerçel sayıların da tanımını vermeyeceğim. Sezgisel olarak, gerçel sayılar, kesirli sayılardan ve kesirli sayıların ”delik”lerinden oluşur. Kesirli sayıların deliklerini doldurduğumuzdan, gerçel sayılar kümesinde ”delik” yoktur.(Tüm bunların tam matematiksel tanımı ve kanıtı vardır elbet.)
Doğal sayılardan tamsayılara, tamsayılardan kesirli sayılara geçerken cebir kullandık. Ama kesirli sayılardan gerçel sayılara geçerken cebir yetersiz kalır, delik doldurmak gibi analitik yöntemlere başvurmak zorundayız.
9. Karmaşık Sayılar
Doğal sayılarda çıkarma yapılamıyordu, tamsayılarda çıkarma yapılabiliyor. Dolayısıyla tamsayılar doğal sayılardan daha az kusurludur.
Tamsayılarda bölme yapılamıyordu, kesirli sayılarda bölme yapılabiliyor. Dolayısıyla kesirli sayılar tamsayılardan daha az kusurludur.
Kesirli sayılarda ”delik”ler vardı, gerçel sayılarda delik yok. Dolayısıyla gerçel sayılar kesirli sayılardan daha az kusurludur.
Gerçel sayılar neredeyse kusursuz… Tek bir kusuru var gerçel sayıların: Gerçel sayılarda $x^2 = -1$ denkleminin çözümü yoktur. Yaratacağız. Bunun için,
1. Gerçel sayıları içeren,
2. Gerçel sayılardan başka $x^2 = -1$ denkleminin bir çözümünü içeren,
3. Toplama ve çarpma gibi iki işlemin olduğu
yeni bir ”sayı kümesi”ne ihtiyacımız var.
Öyle bir sayı kümesinin olduğunu varsayalım. Sayı kümemize $\mathbb C$ diyelim. Birinci koşula göre $\mathbb R \subseteq \mathbb C$ olmalı. İkinci koşula göre, kümemizde $x^2 = -1$ denkleminin bir çözümü var. Bu çözüme $i$ diyelim. Kümede çarpma olduğundan $\mathbb Ri \subseteq \mathbb C$ olmalı. Kümede toplama olduğundan $\mathbb R + \mathbb Ri \subseteq \mathbb C$ olmalı. Göstereceğimiz üzere $\mathbb C$ kümesini $\mathbb R + \mathbb Ri$ olarak, yani
$$\mathbb C = \mathbb R + \mathbb Ri = {a + bi : a, b \in R}$$
olarak alabiliriz. $\mathbb C$ kümesinde toplama ve çarpma şöyle tanımlanmalı:
$$(a + bi) + (c + di) = (a + c) + (b + d)i$$
$$(a + bi) \times (c + di) = (ac – bd) + (ad + bc)i$$
$\mathbb R$ kümesinin tüm cebirsel özellikleri $\mathbb C$ kümesinde de vardır, dahası $\mathbb C$ kümesinde $\mathbb R$’de olmayan $x^2 = -1$ denkleminin bir çözümü vardır.
Yalnız $\mathbb C$ kümesinde $\mathbb R$ kümesinde olduğu gibi bir sıralama yoktur. O kadar kusur kadı kızında da olur!
10. Sonsuz Küçük Sayılar
Gerçel sayılar kümesine geri dönelim.
Gerçel sayılarda $0 < x < 1/2$ denklemini sağlayan birçok sayı vardır, örneğin $1/4$ ya da $1/5$ ya da $1/3$, $1/\pi$…
Gerçel sayılarda $0 < x < 1/3$ denklemini de sağlayan birçok sayı vardır.
Gerçel sayılarda $0 < x < 1/4$ denklemini de sağlayan birçok sayı vardır.
Gerçel sayılarda $0 < x < 1/5$ denklemini de sağlayan birçok sayı vardır.
Ama gerçel sayılarda aşağıdaki sonsuz tane denklemin hepsini birden sağlayan bir $x$ sayısı yoktur:
$0 < x < 1/2$
$0 < x < 1/3$
$0 < x < 1/4$
$0 < x < 1/5$
$0 < x < 1/6$
Belki böyle bir gerçel sayı yok, ama bu, böyle bir ”sayı” yaratamayız anlamına gelmez… Bundan böyle $\varepsilon$, yukarıdaki denklemleri sağlayan bir ”sayı” olsun… $\varepsilon$, tüm pozitif gerçel sayılardan daha küçük ama sıfırdan büyük bir ”sayı”dır. $\varepsilon$ sayısına ”sonsuz küçük” diyebiliriz. Karesini, kökünü alabilir, başka gerçel ya da sonsuz küçük sayılarla toplayabiliriz…
11. Ordinal Sayıları
Bu kez doğal sayılar kümesine geri döneceğiz:
Başlayalım saymaya: $0, 1, 2, 3, 4, 5,\ldots$ Hiç durmadan saymayı sürdürürsek sayıların sonunu getiremeyiz. Sayıların sonu yoktur. Sayıların sonu yoktur; ama öyle bir ”sayı” düşünelim ki bildiğimiz bütün doğal sayılardan daha büyük olsun. Bu pek öyle zor değil. O sayıya bir ad vermek yeterli. $\omega$ (yani ”omega”) olsun yeni sayımızın adı. $\omega$ sayısı bildiğimiz bütün sayılardan daha büyük. 5 binden, 10 binden, 100 binden, milyondan, milyardan; bildiğimiz her sayıdan daha büyük bu $\omega$ sayısı. $\omega$, bir bakıma, sonsuz bir sayı. Bildiğimiz sonlu sayılardan daha büyük bir sayı. $\omega$ sayısını bulduk, belki de yarattık. $\omega$’dan sonra ne gelmeli? $\omega + 1$ gelmeli elbet! Daha sonra da $\omega + 2, \omega + 3, \omega + 4,\ldots$ Şimdiye değin bulduğumuz sayıları yazalım:
$$0, 1, 2, 3, 4,\ldots, \omega, \omega + 1, \omega + 2, \omega + 3, \omega + 4,\ldots$$
Nasıl $0,1,2,3,4,\ldots$ sonlu sayılarından sonra $\omega$’ya rastlamışsak, $\omega, \omega + 1, \omega + 2, \omega + 3, \omega + 4,\ldots$ sayılarından sonra da $\omega + \omega$ sayısına rastlarız. Bu sayıyı $2\omega$ olarak kısaltalım. $2\omega$ sayısından sonra, $2\omega + 1, 2\omega + 2, 2\omega + 3, 2\omega + 4,\ldots$ sayıları gelir. Ya bu sayılardan sonra? $2\omega + \omega$ gelir elbet. Bu sayıyı da $3\omega$ olarak kısaltabiliriz. Bu böyle sürer. Yavaş yavaş $4\omega, 5\omega$ da bulunur.
$\omega, 2\omega, 3\omega, 4\omega$ sayılarından sonra saymayı biliyoruz. Sağına $+1, +2, \ldots$ koymak yetiyor. Bu $\omega$’nın ”katları” olan $\omega, 2\omega, 3\omega, 4\omega\ldots$ sayılarından sonra, $\omega$’nın hangi katı gelir? Nasıl $1, 2, 3, 4,\ldots$ sayılarından sonra $\omega$ geliyorsa, $\omega, 2\omega, 3\omega, 4\omega,\ldots$ gibi $\omega$’nın çarpımlarından sonra $\omega\omega$ gelir. Bu son $\omega\omega$ sayısını $\omega^2$ olarak kısaltalım. $\omega^2$’den sonra $\omega^2 + 1$ geldiğini artık biliyoruz. Daha sonra da $\omega^2 + 2, \omega^2 + 3, \omega^2 + 4,\ldots$ gelir. Arkasından $\omega^2 + \omega$. Sonra $\omega^2 + \omega + 1, \omega^2 + \omega + 2, \omega^2 + \omega + 3,\ldots$ Ta ki $\omega^2+2\omega$’ya gelene dek. Okur sürdürebilir saymayı. $\omega^2 + 3\omega$’ya varacaktır ister istemez. Sonra $\omega^2 + 4\omega$’ya. Saya saya $\omega^2 + \omega^2$’ye, yani $2\omega^2$’ye gelecektir. Bir zaman sonra $3\omega^2, 4\omega^2$ yolumuzun üstüne çıkacaktır. Gide gide $\omega\omega^2$’ye varırız. Bu sayıya $\omega^3$ diyelim.
$\omega, \omega^2, \omega^3,\ldots$ derken $\omega^\omega$ gelir. Bir zaman sonra $(\omega^\omega)^2, (\omega^\omega)^3, (\omega^\omega)^4, (\omega^\omega)^5$ sayılarına rastlarız. Bunları $(\omega^\omega)^\omega$, yani $\omega^{\omega^2}$ izler. Kimse durdurmadığına göre sürdürelim saymayı. $\omega^{\omega^3}$, $\omega^{\omega^4}$ sayılarına varmamızı kimse engelleyemez, dolayısıyla $\omega^{\omega^\omega}$ sayısına da varırız. Sonra $\omega^{\omega^{\omega^\omega}}$, daha sonra $\omega^{\omega^{\omega^{\omega^\omega}}}$ gelir. Bu böyle sürer ve $\omega$’lardan bir kule elde ederiz:
$$\omega^{\omega^{\omega^{\omega^{\omega^{.^{.^{.}}}}}}}$$
Bu sayıya $\varepsilon$ adını verelim. Başka ”sayılar” elde etmeyi okura bırakıyorum.
12. Eğer Matematik Anlaşılmadıysa!
Bu örnekleri okura bilgi vermek amacıyla değil, aşağıdaki amaçlar için verdim:
1. ”Sayı”ları ne kadar özgürce yarattığımızı ve
2. ”Gerçek sayı”larla matematiksel sayılar arasında nasıl bir uçurum olduğunu göstermek istedim.
Umarım bir nebze başarmışımdır. Başaramadıysam bu yazıyı saymayın, sizi matematik bölümümüzün birinci sınıfına beklerim!

