Yazar: E. Mehmet Kıral (erenmehmetkiral@protonmail.com)
Yıl: 2023-1
Sayı: 115
Elinizde 9 top ve bir adet eşit kollu terazi var. Topların biri hariç hepsi türdeş, farklı olanı daha ağır. En az ölçümle ağır olanı nasıl bulursunuz?
Burada dergiyi elinizden düşürün ve düşünün. Söz veriyorum, problemi mesela tıkışık bir otobüs ya da püfür püfür bir feribot yolculuğu boyunca çözmeye uğraştıktan sonra yazının devamını okumak çok daha keyifli olacak.
Hadi bir ipucu daha vereyim, sadece iki tartımda ağır topu elinizle koymuş gibi bulacaksınız. Şimdi gerçekten kapatın sayfayı ama.
Çözüm. Öncelikle topları 1’den 9’a numaralandıralım. Ve 3’er 3’er gruplandıralım. İlk üçlüyü bir kefeye, ikinci üçlüyü diğer kefeye koyalım. Üç ihtimal var; ya soldaki kefe ağır basacak, ya sağdaki, ya da terazi dengede çıkacak:

İlk durumda ağır top 1, 2 ya da 3 numaralı toptan biri. İkinci durumda aranan top ikinci üçlüde. Denge halinde zanlıyı son üç toptan birine kıstırdık. Her halde elimizde üç top var. Üçün herhangi ikisini karşılıklı tartarsak ve bir kefe ağır çekerse, ağır topu bulduk. Terazi dengede çıkarsa da açıkta kalanı işaret ederiz.
Soruyu çözdük. 9 top olmasının bir özelliği var mıydı? Terazi deneyinin sonuçlanabileceği üç konum olduğu için ihtimalleri her sefer üçte birine düşürdük, ve $9 = 3^2$ olduğu için de iki tartımda sonuca ulaştık.
Benzer bir soruyla devam edelim. Elimizde biri zehirli gerisi içilebilir bin kova su var. On adet de deney faremiz var. Yalnız zehir biraz yavaş etkiliyor, zehirli sıvıdan alan fare bir ay sonra ölüyor. En kısa sürede zehirli kovayı nasıl bulabiliriz?
Mesela bir yöntem, tek bir fareye kovalardan suyu teker teker tattırmak. Tabii her tadımdan sonra bir ay beklememiz lazım. En kötü ihtimalle bir ömür sonra hangi kovada zehir olduğunu buluruz. Ya da, madem 10 deney faremiz var, bu yöntemi 10’ar 10’ar da uygulayabiliriz. Bu sefer 83 yıl yerine en kötü sekiz küsur yılda zehri buluruz.
Başka bir yol var mı? Yine durun ve düşünün. Bir ipucu vereceğim, tek ayda zehirli kovayı bulan bir çözüm var. Bu da $10$ fare olması, fare deneyinden çıkabilecek $2$ sonuç olması ve $1000 < 1024 = 2^{10}$ olmasıyla alakalı.
Burada bilgiye dair önemli bir şey var. Bir farenin bir deneyde bize verebileceği bilgi ölmek ya da yaşamak. Tek bir bit kadar bilgi veriyor. Bu arada yeri gelmişken söyleyelim, bir bilgi birimi olarak bit kelimesi ilk defa Shannon’un meşhur makalesinde$^1$ geçiyor ve kendisi kelimenin icadını J. W. Tukey’e atfediyor. Bit, binary digit’ten türetilmiştir.
Bilgi birimi diyerek, bilgi denilen şeyin ölçülebilmesi gibi fantastik bir fikri laf arasında size kabul ettirmiş oldum. Belki de bilgi kelimesini biraz fazla geniş kullanıyorum, tam ne demek istediğimi açıklayayım. Çünkü bahsettiğim şey kesinlikle anlam falan değil, olasılık dağılımlarıyla alakalı.
Sonlu bir olasılık dağılımı olsun, ya da sonlu adet (diyelim $n$) çıktısı olan bir rassal değişken. Bunu, her çıktının ihtimalini yazdığımız bir vektörle ifade edebiliriz: $$\mathbf{p} = (p_1, p_2, \ldots, p_n)$$
Bu vektör $\sum_{i=1}^n p_i = 1$ eşitliğiyle kısıtlı. Böyle her vektör bir olasılık dağılımına karşılık geliyor. Yani $R^n$ içinde köşeleri $(1, 0,0, \ldots, 0)$, $(0,1,0, \ldots, 0)$,$\dots$, $(0,0,\ldots, 0, 1)$ olan bu dışbükey $n-1$ boyutlu geometrik nesnenin —ki kendilerine simpleks denir ve $\Delta^{n-1}$ sembolüyle gösterilir— her bir noktası $n$ adet sonucun mümkün olduğu bir rasgele durumun olasılık dağılımı. Köşeler önemli uç noktalar, o durumda herhangi bir belirsizlik kalmıyor, neyin ne çıkacağını biliyoruz. En bilgisiz olduğumuz dağılım simpleksin orta noktası $\mathbf{p}_0 = (\tfrac1n, \tfrac1n, \ldots, \tfrac 1n)$. Her olasılık hakkında aynı ihtimalle cahiliz, tahmin için zar atsak yeridir. İşte ölçmeye çalıştığımız (gizli) bilgi, önceden bilmediğimiz ve deneyden sonra bileceğimiz arasındaki farka dair bir ”şey” verecek.
Bu ”şey” bir sayı, adına da derler entropi. Sonlu bir olasılık dağılımının entropisi $$H(\mathbf{p}) : = – \sum_{i=1}^n p_i \log p_i$$
formülüyle tanımlanır. Burada bir $i$ için $p_i = 0$’sa, $p_i\log p_i = 0$ kabulünü yapıyoruz, her ne kadar $\log p_i$ anlamlı olmasa da. Ayrıca tüm $p_i$’ler $1$’den küçük olduğu için, $-p_i \log p_i \geq 0$. Entropi, yani $H(p)$ olasılık simpleksinden $R_{\geq 0}$’a giden bir fonksiyon. Entropi’nin $0$’a eşit olduğu tek durumlar, aslında her şeyin belli olduğu, bir belirsizlikten söz edemeyeceğimiz köşe durumları. $H(p)$’nin maksimum olduğu dağılım da $\mathbf{p}_0$ orta noktası (biraz analiz bilgisiyle gösterebilirsiniz). Yani deney sonuçlanınca en çok şeyin aydınlığa kavuştuğu durumlar. Bu iki örnek sonucunda entropi bir olasılık dağılımındaki bilginin —ya da nereden baktığınıza göre bilgisizliğin— makul bir ölçüsü diyebiliriz.
Entropiyi, bir rassal değişkenin sonuçlarına ortalamada ne kadar şaşırdığımızın ölçüsü olarak da düşünebilirsiniz. Bir $X$ rassal değişkeninin alabileceği üç sonuç olsun, ve sonuçların olasılıkları da $\operatorname{P}(X = x_i) =p_i$ olmak üzere, $p_1= 0.9, p_2 = 0.09$ ve $p_3 = 0.01$ olsun. $-\log p_i$ sayısına $X = x_i$ sonucu çıktığında ne kadar şaşırdığımızın ölçüsü dersek, $H(p_1,p_2, p_3)$ entropisi de ortalama şaşkınlığımızı ölçer. Mesela $X = x_3$ çıkarsa gerçekten de şaşırırız, ama bunun çıkma ihtimali de düşük, ve daha olası ve daha az şaşırtıcı olan $X = x_1$ ile dengelenecek.
$H$ fonksiyonu üç özelliği sağlar. Kanıtlayın.
$\quad$a) Her $n$ için $H: \Delta^{n-1} \to R_{\geq 0}$ sürekli fonksiyon,
$\quad$b) $H(\tfrac1n, \ldots, \tfrac 1n) = \log n$ ve bu $n$’nin artan bir dizisi,
$\quad$c) $\mathbf{p} = (p_1, \ldots, p_n)$ herhangi bir olasılık dağılımı ve $\mathbf{q}^1 = (q^1_1, \ldots, q^1_{k_1}), \ldots,\mathbf{q}^n = (q^n_1, \ldots, q^n_{k_n})$ de $n$ adet sonlu olasılık dağılımlarıysa bu dağılımların bileşkesi $\mathbf{p} \circ (\mathbf{q}^1, \ldots, \mathbf{q}^n) \in \Delta^{k_1 + \cdots + k_n -1}$ $$(p_1 q^1_1, \ldots, p_1 q^1_{k_1}, \ldots, p_n q^n_1, \ldots, p_n q^n_{k_n})$$ diye tanımlanır. Bu bileşkenin entropisi $$H(\mathbf{p} \circ (\mathbf{q}^1, \ldots, \mathbf{q}^n)) = H(\mathbf{p})+ \sum_{i = 1}^n p_i H(\mathbf{q}^i)$$ eşitliğini sağlar.
Bunlar sadece $H$’nin birer özelliği değil, aynı zamanda $H$’yi karakterize ediyorlar. Daha doğrusu bu üç özelliği sağlayan bir fonksiyon (ikinci özellikte $H(\tfrac1n, \ldots, \tfrac{1}{n})$’nin arttığını varsaymanız yeterli), bir $c>0$ sabiti için $cH(\mathbf{p})$ formunda olmalı. Kanıt Shannon’un aynı makalesinde (Appendix 2). Bu $c$ sabitini logaritmayı hangi tabanda alacağımızı seçiyoruz diye de düşünebilirsiniz.
Son özelliği bir şekille de gösterebiliriz. Bir olasılık iki adıma ayrılmış olsun. Öncelikle bir zar atacağız, bu $\mathbf{p}$. Sonra bunun sonucuna göre tekrar bir zar (ya da her $i$ sonucuna göre olasılıkları $\mathbf{q}^i$ şeklinde farklı dağılmış zarlar) daha atacağız. Tüm bu işlemin sonundaki bir dağılım elde ediyoruz, işte onun etropisi, ilk adımın entropisi artı ikinci olası adımlardaki entropilerin ağırlıklı toplamı.
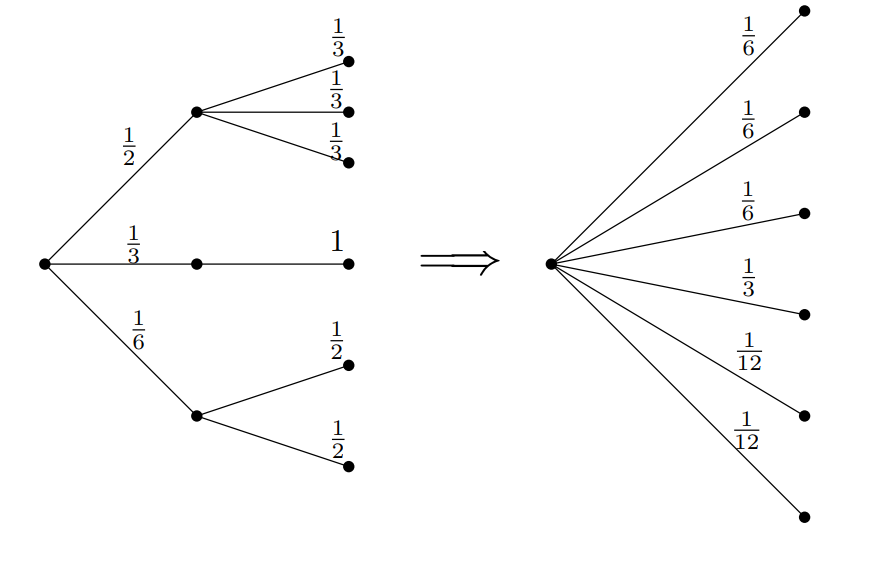
Entropinin bu son özelliğinde kategori teorisi, operadlar, ve bir nevi türev operatörü görüyorsanız… maşallah size. Görmüyorsanız ve bir sebepten görmek istiyorsanız Tai-Danae Bradley’nin yakın zamanda çıkmış makalesine bakabilirsiniz.$^2$
Fareli soruya dönersek, $1000$ kovadan hangisinin zehirli olduğunu bilmediğimiz durumu her $1$’den $1000$’e her birine $1/1000$ ağırlığını veren bir olasılık dağılımı olarak görebilirsiniz. Buradaki belirsizlik $-\sum_{i = 1}^{1000} \tfrac1{1000}\log_2(\tfrac{1}{1000}) = \log_2(1000) \approx 9,965\ldots$. Yani yaklaşık $10$ bit’lik bir belirsizlik var. Buradar farelerle yapılan deneyde çıkabilecek iki sonuç olduğundan logaritmayı $2$ tabanında almak uygun düşüyor. Her bir deney sonucunda yeni bir olasılık dağılımı oluşuyor, yani mesela ilk $500$ sıvıdan almış fare yarı ihtimalle ölecek yarı ihtimalle de yaşayacak. Ölürse demek ki zehir bunlardan birisinde diyoruz, ve yeni ihtimalleri ilk $500$ kovaya $1/500$’den dağıtıyoruz. Yaşarsa yine tekdüze bir olasılık dağılımı var, ama bu sefer son $500$ sıvı arasında. Koşullu olasılık olarak yazarsak, $$\operatorname{P}(n| \times) = \frac{\operatorname{P}(\times |n) \operatorname{P}(n)}{\operatorname{P}(\times)}$$
Bu denklemdeki $n$ sembolü $n$’inci kovanın zehirli olduğu anlamına, $\times$ farenin sizlere ömür olduğunu belirtiyor ($\checkmark$ da yaşadığı anlamına gelsin).
Bu tarz koşullu olasılık denklemlerine Bayes kuralı denir ve yeni öğrenilen bilgiler ışığında olasılık dağılımlarını yenilemede kullanılır. Başlangıçta herhangi bir akıllıca tahminde bulunmak mümkün olmadığı için Laplace’ın izinden gidiyoruz ve tüm kovaları eşit olasılıkla zehirli addediyoruz. Yani her $n$ için $P(n) = 1/1000$. Deneyi yaptık diyelim, ve velev ki fare öldü. Bu bilgiden sonraki yeni $P(n|\times)$ dağılımını bulmak istiyoruz. $n\leq 500$ ise $P(\times | n) = 1$, çünkü zehir ilk beş yüzdeyse, faremiz onu içti, ama bunu bilmeden olasılık $P(\times) = 1/2$’ydi. $n>500$ iken de $P(\times|n) = 0$. Dolayısıyla deney yapılıp da fare öldüğü zaman oluşan yeni olasılık dağılımı $$P(n|\times ) = \begin{cases}\frac{1}{500} & n \leq 500 \text{ ise},\\
0 &n > 500 \text{ ise.} \end{cases}$$
Benzer bir hesapla $$\operatorname{P}(n|\checkmark) = \begin{cases} 0 & n \leq 500 \text{ ise},\\
\frac{1}{500} & n > 500 \text{ ise}.\end{cases}$$
Deney öncesinde ve sonrasındaki entropiye bakalım. Henüz hiçbir şey bilmezken, $H( P(\cdot)) = \log_2 1000$ bit’lik bir belirsizlik içindeyiz. Oysa deneyden sonra hem $H(P(\cdot | \times)) = \log_2 500$ hem de $H(P(\cdot | \checkmark)) = \log_2 500$ bit belirsizliğe düştü, yani deney sonucunda her halükârda tam $$\log_2 1000 – \log_2 500 = \log_2 2 = 1$$
bit kadar bilgi kazanıyoruz. Bu da kazanabileceğimiz en fazla bilgi. Kanıtlayalım.
İki adet rassal değişkenmiz olsun, $X$ ve $Y$. Her iki rassal değişken de sadece sonlu adet çıktı versin. Yukarıdaki fare hesaplarında mesela $X$ zehirli kovanın numarasını veren bir rassal değişken (zehiri hazırlayan kişi için rasgele bir durum olmayabilir, ama siz cahilsiniz, o yüzden size rassal) ve $Y$ de fare deneyi sonucunu veren bir başka değişken.
$X = x_i$ değerlerini alabilir, $Y = y_j$ değerlerini, ve $\operatorname{P}(X = x_i, Y = y_j)$ olasılığını kısaca $p(i,j)$ ile gösterelim ($i = 1.\ldots, N, j = 1, \ldots M$). Aynı mantıkla $p( \cdot| j)$ de $Y = y_j$ gelmesi durumunda $X$’in koşullu olasılık dağılımını veriyor. Tam da bu koşullu olasılığın entropisini hesaplayalım:$$\begin{split} H(X | Y = y_j ) &:= -\sum_{i} p(i | j) \log p(i|j)\\ & \hphantom{:} = -\sum_{i} p(i|j) \log p(i,j) + \sum_{i} p(i|j) \log p(j) \end{split}$$
Bir de ortalamadaki entropiye bakalım. Zira $Y$’nin sonucunun $y_j$ çıkacağı garanti değil, olasılığı $p(j) = \operatorname{P}(Y = y_j) = \sum_i p(i,j)$. $H(X|Y)$ diye gösterilen ve koşullu entropi diye adlandırılan sayı tam da $Y = y_j$’ler üzerinden ortalama alınca çıkan miktar: $$\begin{split} H(X|Y) & := \sum_j p(j) H(X| Y = y_j) \\ & \hphantom{:} = -\sum_{i,j} p(i,j) \log p(i,j) + \sum_{i,j} p(i,j) \log p(j) \end{split}$$
Burada ilk terim tüm olasılıkların masada olduğu bileşik olasılık dağılımının entropisi $H(X,Y)$, ikinci terimdeyse $i$’leri toplayip $\sum_j p(j) \log p(j) = -H(Y)$ elde ediyoruz. Yani özetle,$$ H(X, Y) – H(Y) = H(X|Y).$$
$Y$ rassal değişkeninin farenin yaşayıp öldüğünü vermesi örneğine geri dönecek olursak; $H(Y)$’nin alabileceği maksimum değer $\log_2 2 = 1$ bit, o da $\times$ ve $\checkmark$ ihtimalleri eşit olursa. Demek ki sol tarafta başlangıç entropisinden en fazla $1$ bit düşebiliyormuşuz. Genel olarak $Y$ deneyini, $H(Y)$’nin maksimum değeri $\log_2 M$’ye olabildiğince yakın olacak şekilde dizayn edersek, başlangıç entropisini o kadar azaltabiliriz. Mesela sonucun baştan ne çıkacağını bildiğimiz bir deney bize hiçbir bilgi vermez, zaten $H(Y)$ de sıfır olur. Onun yerine —koşullar elverdiğince— $\operatorname{P}(Y = y_j)$ olasılıklarını $1/m$’ye yakın tutmaya çalışmalıyız.
Sağ tarafta da bir ortalama var, deneyin sonucu ne olursa olsun ortalamadaki terimlerin olabildiğince düşük olmasını istiyoruz. Yani ortalamada değil de deneyin sonucu ne çıkarsa çıksın, ihtimallerin entropisi olabildiğince düşsün, sis perdesi aralansın. Bu da ortalamaya katılan tüm $H( X | Y = y_j)$ entropilerinin eşit, ya da birbirlerine olabildiğince yakın olmasıyla mümkün. Geri kalan tüm durumlarda deneyin öyle bir sonucu çıkar ki, o sonuç altındaki $H(X| Y = y_j)$ entropisi bu ortalamadan yüksek olur. Yani $$\max_j \left\{ H(X | Y = y_j) \right\} \geq H(X,Y) – \log M.$$
Eğer deneyin sonucu ne çıkarsa çıksın belli bir miktarda aydınlanma yaşamayı garantilemek istiyorsak düşüp düşebileceğimiz entropi bu.
Fareli sorunun çözümü. $1$’den $1000$’e kadar olan sayıları ikilik tabanda yazın, toplam 10 basamak gerekli. Her bir fareyi $0$’dan $9$’a kadar numaralandıralım. Her bir fare tek bir basamağı temsil etsin, ve her fare kendi basamağında $1$ değeri olan kovalardan içsin. Mesela iki yüz on yedinci kova iki tabanında $(0011011001)_2 = 2^7 + 2^6 + 2^4 + 2^3 + 2^0$ biçiminde yazıldığı için $0,3,4,6,7$ numaralı deney fareleri bu kovadaki sıvıyı içecek. Her bir kova için bu işlemi tekrarlayacağız. Sonuçta ölen farelerin numaralarından zehirli kovanın sıra numarasını ikilik tabanda okuyabileceğiz.
Şimdi bu bilgi sayan yeni birimimizi kuşanıp, tartı probleminin bir varyasyonunu çözelim. Tartının olası üç çıktısı olduğu için $( \swarrow,\, \searrow,\, \longleftrightarrow )$ logaritmayı $2$ değil $3$ tabanında alalım. Yani bilgiyi bit’le değil, trit’le sayalım. Bu seçimin İstanbul Ankara yolunu kilometreyle mi, santimetreyle mi, mille mi saymışsınız ondan farkı yok. Sayılar değişebilir ama mesafe değişmiyor.
Bu sefer elinizde $12$ adet küre olsun, biri hariç hepsi türdeş, ancak bu sefer farklı olanın ağır mı hafif mi olduğunu bilmiyorsunuz. En az kaç tartımda hangi kürenin farklı ve ağır mı hafif mi olduğunu bulunuz.
Çözüm. İlk önce küreleri $1$’den $12$’ye numaralandıralım, ve ilk dörtlüyle ikinci dörtlüyü ayrı keselere koyalım. Üç ihtimal var:

İlk iki durum simetrik, isimlendirmeyi değiştirerek ilk duruma indirgeyebliiriz. Üçüncü halde farklı olan top son dörtlüden biri, ve ağır mı hafif mi olduğunu bilmiyoruz, yani $\log_3 8$ trit kadar bir belirsizliğimiz var. Neyse ki bu $2$’den küçük ve dolayısıyla problemi çözme ihtimalimiz var. Mesela $9-10-11$ numaralı topları alıp tekdüze ağırlıkta olduğunu bildiğimiz $1-2-3$ toplarına karşı tartarsak; sol kefe ağır çekerse $9-10-11$’den birinin farklı, ve farklı olmanın ağır demek olduğunu bileceğiz, hafif çekerse yine bu üçlüden birinin hafif olduğunu bileceğiz. Her iki durumda da soru ilk soruda sorduğumuz üçlünün birini bulma problemine düşüyor, onu da tek tartımda çözebiliyoruz. Kefeler eşit gelirse de farklı olan $12$ numaralı küre, ama onun da hafif mi ağır mı olduğunu belirlemek için (yani $\log_3 2$ kadar bir belirsizliği gidermek için) temiz bir küreye karşı tartmamız yeter. Şimdi
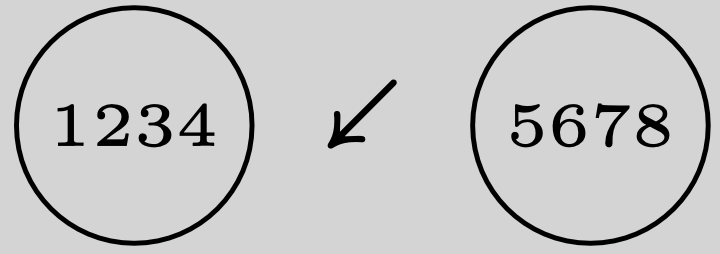
durumunu ele alalım. Bu durumda enteresan bir şey yapmamız gerekiyor. Aklımızın bir köşesinde tartı deneyimizin her sonucunda en fazla $1$ tritlik belirsizlik kalması gerektiğini hatırlayalım. Terazinin bir tarafına $1-2-3-5$ (yani üç adet potansiyel ağır, ve bir adet potansiyel hafif top) diğer tarafına da $4-10-11-12$ toplarını koyalım. Sonuç yine üç türlü çıkabillir. İlk kefe ağır çekerse $1-2-3$’ten biri ağır ve hangisi olduğunu tek tartımda bulmayı biliyoruz. Hafif çekerse, ya $5$ hafif ya da $4$ ağır. Bu durumda belirsizlik $\log_3 2$, yani bir tritten az, ama olsun ucu ucuna başlamamıştık, birazcık hata payımız var. Her tartımın taşını sıkıp bilgisini sonuna kadar çıkartmamıza gerek yok. Bu ikinci durumda $5$ ve $9$ numaralı topları karşılaştırarak (mesela) iki durumdan hangisinde olduğumuzu bulabiliriz. Son olarak çift kollu terazi dengede çıkabilir. Bu durumda tek ihtimal farklı olan topun hafif olması, ve o da $6-7-8$’den biri. Bu hali de tek bir tartımda altedebiliyoruz.
Şimdi size sorular geliyor. Aynı soruyu $13$ topla yapabilir miyiz? Entropi baştan bize $14$ topla yapamayacağımızı söylüyor, çünkü $14$ toptan her biri ağır ya hafif ya ağır $28$ farklı durum var, entropi de $\log_3 28 \approx 3.0331\cdots > 3$ trit. Her bir tartımda belirsizlikten fazla $1$ trit düşebiliyoruz. Yani bu soru $14$ topla $3$ tartımda imkansız.
$13$ top sorusunda böyle kaba hesap entropik mülahazalar bize ket vurmuyor, yapamazsın demiyor. Yapabilirsin de demiyor, bizi sonuca götürecek tartım planı ayrı bir soru.
Dışarıdan ağır ya da hafif olmayan bir top ekleyerek soruyu çözmek mümkün. Yeni topun ne menem bir şey olduğunu tam olarak biliyoruz, yani yeni bir top dahil ederek ekstradan belirsizlik eklemedik, entropi anlamında soruyu zorlaştırmadık. Ama $13$ toplu soru dışarıdan bir top eklemeden de mümkün değil, bunu da olası ilk tartımlar sonucunda entropileri hesaplayarak görebilirsiniz: birer, ikişer, üçer, dörder, beşer, nasıl tartarsanız tartın, tartımın bir sonucunda (her sonucunda değil) eldeki entropi $2$ tritten fazla oluyor.
Bu son ikisini de gerçekten sizlere bırakıyorum. Eğlenin. Çözümü bulduktan sonra ortamlarda soruyu sorarsınız, büyük sükse yapacağınızı garanti ediyorum.$^3$
$^1$ “A Mathematical Theory of Communication”, Bell System Technical Journal, 27(3), 1948.
$^2$ “Entropy as a topological operad derivation”. Entropy, 23(9), 2021.
$^3$ … ya da yanlış ortamlardasınız.


