Yazarlar: Alp Eden ve Ersin Karabudak
Yıl: 2023-1
Sayı: 115
1. Hüseyin Tevfik Paşa’nın Lineer Cebir Kitabı
Hüseyin Tevfik (1832-1901) Bulgaristan’a bağlı olan Vidin şehrinde dünyaya geliyor. Eğitiminin büyük bir bölümünü askeri okullarda tamamladı. Mekteb-i Harbiye’de hocası olan Tahir Beyin de desteğiyle daha okulda öğrenciyken onun matematik derslerine yardımcı oluyor. Paris’e askeri ateşe olarak gönderilene kadar Mekteb-i Harbiye’de matematik dersleri vermeye devam ediyor. Hayatının değişik dönemlerinde askeri görevlerinin yanı sıra değişik okullarda matematik hocalığı da yapıyor. 1872-1878 yılları arasında, kısa aralıklar dışında, Amerika Birleşik Devletleri’nde askeri/diplomatik görevlerde bulunuyor. 1882 yılında İstanbul’da (Constantinople) İngilizce olarak yayımlanan Linear Algebra kitabını Amerika’da (Rhode Island) yazmaya başlıyor. 1883-1886 yılları arasında Washington’da orta elçilik görevini üstleniyor. Amerika’dan döndükten sonra ölümüne kadar Osmanlı İmparatorluğu’nda değişik yüksek düzeyli bürokratik görevlerde bulunuyor (daha detaylı biyografisi için bkz. Çeçen 1988, Polat 2019). 1892 yılında Linear Algebra kitabının ikinci ve genişletilmiş bir baskısını yayınlıyor.
1882 yılında İstanbul’daki Boyajian Matbaası’nda İngilizce olarak yayımlanan Linear Algebra kitabı 69 sayfadan oluşuyor. Kitabın ikinci bölümünde tanımlanan ve özellikleri incelenen “linear multiplication” kanımızca kitaptaki en özgün neticeleri içeriyor. Bu lineer çarpıma yazımızda hem vektör çarpımı hem de Vidinli’nin çarpımını anımsattığ için $v$-çarpımı diyeceğiz. Bu terimin isim babası Şahin Koçak’tır. Linear Algebra kitabının ikinci baskısı genişletilmiş ve düzeltmiş olarak 187 sayfaya çıkıyor. Lineer cebir kitabının ikinci baskısı sekiz bölümden oluşmaktadır. İlk bölümde vektör uzayının cebirsel özellikleri tanıtılıyor. İkinci bölümünde üç boyutlu vektörler için bir çarpım, ilk önce geometrik olarak sonra da cebirsel olarak tanımlanıyor (bkz. Linear Algebra 1892, s. 27). Üçüncü bölümde tanımlanan “özel dikey” vektörü aslında iki vektörün dış çarpımının geometrik tanımıdır (Linear Algebra 1892, s. 47). Aynı bölümde iç çarpım Vidinli’nin tanımladığı vektör çarpımı cinsinden elde edilmiştir (Linear Algebra 1892, s. 46). Kitabın dördüncü bölümü iki boyutta analitik geometriye çeşitli uygulamalar içermektedir. Beşinci bölümde bu uygulamalar üç boyutta yapılmıştır. Altıncı bölümde ikinci dereceden genel denklemler inceleniyor ve bunların iki boyutlu yüzeylerle ilişkisi kuruluyor. Yedinci bölümde türev almakla ilgili bilgiler verildikten sonra bazı uzay eğrileri hakkında uygulamalar sunuluyor. Son bölümde kuaterniyonlar daha genel olan “karmaşık niceliklerin” (complex quantities) özel bir durumu olarak sunuluyor. Kitapta verilen çarpım da karmaşık niceliklerin çarpımının özel bir durumu olarak ele alınıyor ve bu iki çarpım uygulamalar üzerinde kıyaslanıyor.

19. yüzyılın ikinci yarısında lineer cebir ve vektör analizi/cebiri konuları henüz bugünkü olgunluklarına ulaşmamışlardı. 1843 yılında William Rowan Hamilton (1805-1865) uzun seneler boyunca üç boyutta bir vektör çarpımını tanımlamaya çalışıp başaramadıktan sonra, dördüncü boyuta geçerek kuaterniyon çarpımını tanımlar. Bugün, üç boyutta bölme cebiri (division algebra) olmadığını biliyoruz. 19. yüzyılda Hamilton’ın da etkisiyle uzunca bir süre vektör cebirleri konusuyla kuaterniyon cebiri konusunun örtüştüğü tezi savunuluyor (bkz. Crowe 1994). 1867 yılında Hamilton’ın bölümdaşı Peter Guthrie Tait kuaterniyonlara giriş kitabını yayımlıyor. Vidinli kitaplarında Tait’in kitabına hem referans veriyor hem de onunla hesaplaşıyor. Vidinli’nin temel tezi üç boyutta vektör cebiri yapmanın mümkün olduğu ve bunu yapmak için kuaterniyon kavramına ihtiyaç olmadığıdır. Vidinli’nin tanımladığı vektör çarpımı ne değişim ne de birleşim özelliklerini sağlıyor. Çarpımın sağladığı temel özellik toplama üzerine dağılım özelliğidir. Vidinli’nin kitabı üzerinde alıntılanan üç yorum var: Cahit Arf’ın kısa değerlendirmesi birleşim özelliğini sağlamadığı için bu cebirin kullanışlı bir cebir olmadığı yönündedir (Çeçen 1988, s. 47). Schubring (2007) ve Tezer (2015) ise bu cebir ile çalışılabileceğini, yani matematik yapılabileceğini, belirtiyorlar. Yaklaşımımız bu üç “yorumu” da kısmen de olsa haklı çıkartıyor; yani Nasreddin Hoca’nın dediği gibi herkes “haklı”.
Bir süredir Linear Algebra kitabı üzerinde bir çalışma yürütüyoruz. Temel amacımız Vidinli’nin kitabındaki neticeleri günümüz bilgileri ışığında alternatif bir şekilde ifade etmek ve anlamak. Vidinli’nin kitabını yazdığı zamanlarda gerek iç çarpımın (dot product) gerekse dış çarpımın (cross product) üzerinde bilgiler yaygın kullanımda olmasa da biliniyordu (Crowe 1994). Vidinli de kitabında kendi çarpımı ile iç ve dış çarpımlar arasındaki ilişkiler hakkında ipuçları veriyor. Vidinli kitabında dış çarpım yerine “özel dik” (special perpendicular) ifadesini kullanıyor, ama ne yazık ki bu çıkan vektörü kendi çarpımıyla ilişkilendirmiyor.
Her ne kadar yazımızın temel amacı iç ve dış çarpımlarla Vidinli çarpımı ve kuaterniyon çarpımı arasındaki ilişkileri irdelemek olsa da kitapta verilen bazı neticelerle birlikte yeni neticeler de sunmaya çalıştık. Sunduğumuz alternatif ifadelerin kitaptaki çerçeveyi ve uygulamaları büyük ölçüde rahatlatacağını umuyoruz. Çalışmamızın başka çalışmalara ön ayak olması en büyük arzumuzdur.
2. İç ve dış çarpımın tanımları ve bazı özellikleri
Üç boyutlu vektörlerin iç ve dış çarpımlarının yazıda kullandığımız bazı özelliklerini hatırlatarak başlayalım. Bu özellikler vektör analizini işleyen kitaplarda kolaylıkla bulunabilir (örneğin bkz. Marsden ve Tromba 2012). olsun.
$a=\left(a_{1}, a_{2}, a_{3}\right)$ ve $b=\left(b_{1}, b_{2}, b_{3}\right)$ olarak verilmiş olsun.
- İki vektörün iç çarpımı şu şekilde tanımlanır: $$ a \cdot b=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3} $$
- Bir vektörün normu şu şekilde tanımlanır: $$ \|a\|^{2}=a \cdot a=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}$$
- Eğer $a$ ve $b$ arasındaki açı $\phi$ ise $a \cdot b=$ $\cos \phi\|a\| \|b\|$ eşitliği sağlanır.
- Dönme ve yansıma dönüşümleri iç çarpımı korur.
- İki vektörün dış çarpımı şu şekilde tanımlanır: $$ a \times b=\left(a_{2} b_{3}-a_{3} b_{2},\, a_{3} b_{1}-a_{1} b_{3},\, a_{1} b_{2}-a_{2} b_{1}\right) $$
- Dış çarpım ters değişme özelliğini sağlar: $a \times b=$ $-b \times a$.
- $a \times b$ vektörü $a$ ve $b$ vektörlerine diktir. Normlar arasında $\|a \times b\|=|\sin \phi| \|a\| \|b\|$ ilişkisi vardır.
- Dönme dönüşümleri dış çarpımı korur.
- $a \cdot(b \times c)$ ifadesine $a, b, c$ vektörlerinin üçlü çarpımı adı verilir.
- Satırları verilen üç vektörden oluşan matrisin determinantı vektörlerin üçlü çarpımını verir. $$ a \cdot (b \times c) = \left| \begin{array}{ccc} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{array} \right|$$
- Üçlü çarpımın mutlak değeri üç vektörün belirlediği paralelyüzlünün hacmine eşittir.
- Üç vektörün lineer bağımlı olması $a \cdot(b \times c)=0$ koşulu ile eşdeğerdir.
3. Vidinli çarpımının temel özellikleri
Vidinli üç boyutlu vektörler üzerinde $v$-çarpımını başta geometrik olarak tanımlıyor (Linear Algebra 1892, s. 15). Çarpımın bazı temel özelliklerini bu tanımdan yola çıkarak gösteriyor. Çift lineerlik özelliğinin sağlandığı gösterildikten sonra, $v$-çarpımı üç tane baz vektörü üzerinde bir çarpım tablosu verilerek tanımlanabiliyor (Linear Algebra 1892, s. 23):
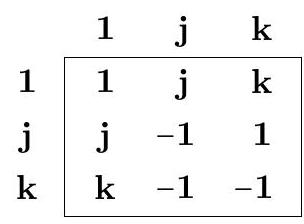
Burada $\mathbf{1}$, $\mathbf{j}$ ve $\mathbf{k}$ vektörleri üç boyutlu uzayda ortonormal bir baz oluşturuyor. Vidinli kitabında bunları $\mathbf{i}$, $\mathbf{j}$ ve $\mathbf{k}$ sembolleriyle göstermiş. $v$-çarpımının birim elemanı olduğu için, biz $\mathbf{i}$ yerine $\mathbf{1}$ sembolünü kullanmayı tercih ettik.
Vidinli $v$-çarpımını göstermek için üç değişik notasyon kullanıyor: $a b$, $a \times b$, $a \cdot b$ (Linear Algebra 1892, s. 16). Bu da kitabının okunmasını oldukça güçleştiriyor. Bu yazıda $v$-çarpımı için $\underline{\vee}$ sembolünü kullanacağız.
Çarpım tablosunu ve dağılma özelliğini kullanarak $a=a_{1} \mathbf{1}+a_{2} \mathbf{j}+a_{3} \mathbf{k}$ ve $b=b_{1} \mathbf{1}+b_{2} \mathbf{j}+b_{3} \mathbf{k}$ vektörlerinin $v$-çarpımını şu şekilde yazabiliyoruz (Linear Algebra 1892, s. 27):
$$ a \underline{\vee} b=( a_{1} b_{1}-a_{2} b_{2}-a_{3} b_{3}+a_{2} b_{3}-a_{3} b_{2}) \mathbf{1} +(a_{1} b_{2}+a_{2} b_{1}) \mathbf{j} +(a_{1} b_{3}+a_{3} b_{1}) \mathbf{k} \tag{1}$$
$v$-çarpımının bazı özellikleri çarpım tablosundan kolaylıkla görülebilir:
- $\mathbf{1}$ vektörü $v$-çarpımının birim elemanıdır.
- $v$-çarpımı değişme özelliğini sağlamaz: örneğin $\mathbf{j} \underline{\vee} \mathbf{k} \neq \mathbf{k} \underline{\vee}\mathbf{j}$.
- $v$-çarpımı birleşme özelliğini sağlamaz: örneğin $\mathbf{j} \underline{\vee}(\mathbf{j} \underline{\vee}\mathbf{k}) \neq(\mathbf{j} \underline{\vee}\mathbf{j}) \underline{\vee} \mathbf{k}$.
- $v$-çarpımı sadeleşme özelliğini sağlamaz: örneğin $\mathbf{j} \neq \mathbf{k}$ olmasına rağmen $\mathbf{k} \underline{\vee} {\mathbf{j}}=\mathbf{k} \underline{\vee} \mathbf{k}$. Buradan $v$-çarpımında sıfır bölenler olduğunu da görüyoruz: $\mathbf{k} \underline{\vee}(\mathbf{j}-\mathbf{k})=0$.
Vidinli $1$ vektörünün katlarını “principal direction” olarak adlandırmış. Biz buna birincil yön veya birincil eksen diyeceğiz.
Bir vektörün eşleniğini şu şekilde tanımlıyoruz (Linear Algebra 1892, s. 30):
$$
\bar{a}=a_{1} \mathbf{1}-a_{2} \mathbf{j}-a_{3} \mathbf{k}
$$
Eşlenik dönüşümü birincil eksen etrafında $180^{\circ}$ dönmeye karşılık geliyor.
$v$-çarpımının yukarıda verilen cebirsel ifadesini $(1)$ kullanarak
$$
\bar{a} \underline{\vee} a=a \underline{\vee}\bar{a}=\left(a_{1}^{2}+a_{2}^{2}+a_{3}^{2}\right) \mathbf{1}=\|a\|^{2} \mathbf{1} \tag{2}
$$
olduğu gösterilebilir (Linear Algebra 1892, s. 30). Eğer $a^{\prime}=\bar{a} /\|a\|^{2}$ dersek, $(2)$ eşitliğinden
$$
a^{\prime} \underline{\vee} a=a \underline{\vee} a^{\prime}=\mathbf{1}
$$
olduğu görülür. Yani sıfırdan farklı her vektörün $v$-çarpımına göre bir tersi vardır. Ancak $v$-çarpımı birleşme özelliğini sağlamadığı için, $a \underline{\vee} x=b$ şeklindeki bir denklemi her iki tarafı $a^{\prime}$ ile çarparak çözmek mümkün değil.
4. $v$-çarpımının iç ve dış çarpımlar kullanılarak gösterimi
Bu bölümde $v$-çarpımının iç ve dış çarpımlar cinsinden ifade edilebildiğini göreceğiz.
İki vektörün iç ve dış çarpımlarını yazalım:
$$
\begin{aligned}
a \cdot b= & a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3} \\
a \times b= & \left(a_{2} b_{3}-a_{3} b_{2}\right) \mathbf{1}+\left(a_{3} b_{1}-a_{1} b_{3}\right) \mathbf{j} +\left(a_{1} b_{2}-a_{2} b_{1}\right) \mathbf{k}
\end{aligned}
$$
Son eşitliği geçici olarak şu şekilde ifade edelim:
$$
a \times b=p \mathbf{1}+q \mathbf{j}+r \mathbf{k}
$$
Şimdi $\bar{a}=a_{1} \mathbf{1}-a_{2} \mathbf{j}-a_{3} \mathbf{k}$ ve $b$ vektörlerinin $v$-çarpımını $(1)$ eşitliğini kullanarak şu şekilde yazabiliriz:
$$
\begin{aligned}
\bar{a} \underline{\vee} b= & \left(a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}-a_{2} b_{3}+a_{3} b_{2}\right) \mathbf{1} +\left(a_{1} b_{2}-a_{2} b_{1}\right) \mathbf{j} +\left(a_{1} b_{3}-a_{3} b_{1}\right) \mathbf{k} \\
= & (a \cdot b) \mathbf{1}-p \mathbf{1}+r \mathbf{j}-q \mathbf{k} \\
= & (a \cdot b) \mathbf{1}-R(a \times b) \hphantom{-a_{2} b_{3}+a_{3} b_{2}) \mathbf{1} +\left(a_{1} b_{2}-a_{2} b_{1}\right) \mathbf{j} +\left(a_{1} b_{3}-a_{3} b_{1}\right) \mathbf{k}} \qquad \qquad (3)
\end{aligned}
$$
Son satırda $R(p \mathbf{1}+q \mathbf{j}+r \mathbf{k})=p \mathbf{1}-r \mathbf{j}+q \mathbf{k}$ olarak tanımlanan bir lineer dönüşüm kullanıyoruz. Bu dönüşüm sürekli olarak karşımıza çıkacak. Dolayısıyla bu noktada özelliklerini listelememiz gerekiyor.
- $R$ birincil eksen etrafında $90$ derecelik bir dönmedir. ($\mathbf{1}$, $\mathbf{j}, \mathbf{k}$ vektörlerinin sağ-elli bir baz oluşturduğunu kabul edersek, bu dönme birincil eksenden başlangıç noktasına doğru bakıldığında saat yönünün tersinedir. Bu yönü pozitif yön olarak kabul edeceğiz.)
- $R$ eşlenik işleminin kareköküdür: yani her $a$ için $R^{2} a=\bar{a}$ eşitliği vardır.
- $R$ dönüşümü $R^{4}=I$, ve $R^{-1}=R^{3}$ eşitliklerini sağlar.
- $R$ bir dönme olduğu için iç ve dış çarpımları korur.
Son olarak, $(3)$ eşitliğinde $\bar{a}$ yerine $a$ yerleştirerek şu sonuca ulaşırız:
Gözlem 1. İki vektörün $v$-çarpımı vektörlerin iç ve dış çarpımlarını kullanarak şu şekilde yazılır:
$$
a \underline{\vee} b=(\bar{a} \cdot b) \mathbf{1}-R(\bar{a} \times b) \tag{4}
$$
5. Birincil dönmeler altında $v$-çarpımı
Üç boyutlu uzayda her dönmenin iç ve dış çarpımları koruduğunu biliyoruz. $v$-çarpımı için böyle genel bir sonuç bekleyemeyiz; çünkü $v$-çarpımını koruyan bir dönüşümün $\mathbf{1}$ vektörünü kendisine götürmesi gerekir. Bu özelliği sağlayan dönmelere birincil dönme diyeceğiz.
$S$ herhangi bir birincil dönme olsun. $R$ ve $S$ aynı dönme eksenini paylaştıkları için sıraları değiştirilebilir: $R S=S R$.
$S$ dönüşümünü $(4)$ eşitliğine uygulayarak
$$
\begin{aligned}
S(a \underline{\vee} b) & =\left(R^{2} a \cdot b\right) S \mathbf{1}-S R\left(R^{2} a \times b\right) \\
& =\left(R^{2} a \cdot b\right) \mathbf{1}-R S\left(R^{2} a \times b\right)
\end{aligned}
$$
elde ederiz. $S$ dönüşümü iç ve dış çarpımları koruduğu için
$$
\begin{aligned}
R^{2} a \cdot b & =R^{2} S a \cdot S b \\
S\left(R^{2} a \times b\right) & =R^{2} S a \times S b
\end{aligned}
$$
eşitlikleri geçerlidir. Bunları kullanarak
$$
\begin{aligned}
S(a \underline{\vee} b) & =\left(R^{2} S a \cdot S b\right) \mathbf{1}-R\left(R^{2} S a \times S b\right) =S a \underline{\vee} S b
\end{aligned}
$$
sonucunu elde ederiz. Yani birincil dönmeler $v$-çarpımını korur.
6. İç çarpımın $v$-çarpımı ile ilişkisi
Gözlem 2. İki vektörün iç çarpımı, $v$-çarpımı cinsinden şu şekilde ifade edilebilir:
$$
(a \cdot b) \mathbf{1}=\frac{1}{2}(\bar{a} \underline{\vee} b+\bar{b} \underline{\vee} a) \tag{5}
$$
Kanıt. $(4)$ eşitliğini kullanarak
$$
\bar{a} \underline{\vee} b=(a \cdot b) \mathbf{1}-R(a \times b) \tag{6}
$$
ve
$$ \bar{b} \underline{\vee} a =(b \cdot a) \mathbf{1}-R(b \times a) =(a \cdot b) \mathbf{1}-R(-a \times b) =(a \cdot b) \mathbf{1}+R(a \times b) \tag{7} $$
yazabiliriz. Bu iki eşitliğin toplamı bize
$$
\bar{a} \underline{\vee} b+\bar{b} \underline{\vee} a=2(a \cdot b) \mathbf{1}
$$
eşitliğini verir. $\qquad \qquad \square$
Bu ilişkiyi Vidinli kitabında göstermiş (Linear Algebra 1892, s. 31) ve daha sonraki bölümlerde, özellikle geometrik uygulamalarda, $v$-çarpımını çoğunlukla $(\bar{a} \underline{\vee} b+\bar{b} \underline{\vee} a)$ şeklindeki ifadeler içinde kullanmış.
7. Dış çarpımın $v$-çarpımı ile ilişkisi
Gözlem 3. İki vektörün dış çarpımı şu şekilde ifade edilebilir:
$$
a \times b=(a \cdot b) \mathbf{1}-R(a \underline{\vee} \bar{b}) \tag{8}
$$
Kanıt. $(6)$ eşitliğini şu şekilde yazalım:
$$
R(a \times b)=(a \cdot b) \mathbf{1}-\bar{a} \underline{\vee} b
$$
Buna $R^{3}=R^{-1}$ dönüşümünü uygulayalım:
$$
a \times b=(a \cdot b) R^{3} \mathbf{1}-R^{3}(\bar{a} \underline{\vee} b)
$$
$R^{2}$ dönüşümü $v$-çarpımını koruduğu için
$$
R^{3}(\bar{a} \underline{\vee} b)=R\left(R^{2} \bar{a}\underline{\vee} R^{2} b\right)=R(a \underline{\vee} \bar{b})
$$
yazabiliriz. Bunu bir önceki eşitliğe yerleştirerek $(8)$ sonucunu elde ederiz. $\qquad \qquad \square$
Gözlem 4. İki vektörün dış çarpımı $v$-çarpımı kullanarak şu şekilde de ifade edilebilir:
$$
a \times b=\frac{1}{2} R(b \underline{\vee} \bar{a} -a\underline{\vee} \bar{b}) \tag{9}
$$
Kanıt. $(6)$ eşitliğini $(7)$ eşitliğinden çıkararak
$$
2 R(a \times b)=\bar{b} \underline{\vee} a-\bar{a} \underline{\vee} b
$$
elde ederiz. Her iki tarafa $\frac{1}{2} R^{3}$ dönüşümü uygulandığında $(9)$ eşitliği çıkar. $\qquad \qquad \square$
8. Sıfır bölenler düzlemi
Bu bölümde $v$-çarpımının tüm sıfır bölenlerinin kümesinin ( $\mathbf{j}, \mathbf{k})$ düzlemi olduğunu göreceğiz.
Gözlem 5. $v$-çarpımının soldan ya da sağdan sıfır bölenleri sadece $(\mathbf{j}, \mathbf{k})$ düzleminde olabilir.
Kanıt. $a \underline{\vee} b=0$ olduğunu varsayalım. $(4)$ eşitliğini kullanarak bunu
$$
(\bar{a} \cdot b) \mathbf{1}-R(\bar{a} \times b)=0
$$
ya da
$$
R(\bar{a} \times b)=(\bar{a} \cdot b) \mathbf{1}
$$
olarak yazabiliriz. $R^{-1}$ dönüşümünü uygulayarak
$$
\bar{a} \times b=(\bar{a} \cdot b) \mathbf{1} \tag{10}
$$
eşitliğini elde ederiz. İki vektörün dış çarpımı her iki vektöre de dik olduğu için, buradan $\bar{a} \cdot \mathbf{1}=a_{1}=0$ ve $b \cdot \mathbf{1}=b_{1}=0$, yani $a$ ve $b$ vektörlerinin $(\mathbf{j}, \mathbf{k})$ düzleminde olduğu sonucu çıkar. $\square$
$\bar{a}$ ile $b$ arasındaki açı $\phi$ olsun. $(10)$ eşitliğinin iki tarafının normlarını yazarak
$$
\begin{aligned}
\|\bar{a} \times b\| & =\|(\bar{a} \cdot b) \mathbf{1}\|=|\bar{a} \cdot b| \\
|\sin \phi|\|a\|\|b\| & =|\cos \phi|\|a\|\|b\| \\
|\sin \phi| & =|\cos \phi|
\end{aligned}
$$
eşitliklerini elde ederiz. Sonuncu eşitlik $n$ tamsayı olmak üzere $\phi=\pi / 4+n \pi / 2$ değerleri için doğrudur. Yani $\bar{a}$ ile $b$ arasındaki açının $45^{\circ}$ veya $135^{\circ}$ olması gerekir. $\bar{a}=-a$ olduğu için aynı sonuç $a$ ve $b$ için de geçerlidir.
Gözlem 6. $(\mathbf{j}, \mathbf{k})$ düzlemindeki her vektör bir sıfır bölendir.
Kanıt. $a=a_{2} \mathbf{j}+a_{3} \mathbf{k}$ olsun. $a$ ile arasında $45^{\circ}$ olan $b=\left(a_{2}-a_{3}\right) \mathbf{j}+\left(a_{2}+a_{3}\right) \mathbf{k}$ vektörünü alalım. $a$ sıfır değilse $b$ de sıfır değildir ve $a \underline{\vee} b=0$ eşitliği sağlanır. $\quad \square$
9. Normlarla $v$-çarpımı arasında bir ilişki
Gözlem 7. İki vektörün $v$-çarpımının normu şu eşitsizliği sağlar:
$$
\|a \underline{\vee} b\| \leq \sqrt{2}\|a\|\|b\|
$$
Kanıt. $(4)$ eşitliğine üçgen eşitsizliğini uygulayarak
$$
\|a \underline{\vee} b\| \leq\|(\bar{a} \cdot b) \mathbf{1}\|+\|R(\bar{a} \times b)\| \tag{11}
$$
yazabiliriz. $\bar{a}$ ile $b$ arasındaki açıya $\phi$ diyelim. Sağ taraftaki ilk terimi
$$
\begin{aligned}
\|(\bar{a} \cdot b) \mathbf{1}\| & =|(\bar{a} \cdot b)|=|\cos \phi|\|\bar{a}\|\|b\| \\
& =|\cos \phi|\|a\|\|b\|
\end{aligned}
$$
olarak, ikinci terimi de
$$
\begin{aligned}
\|R(\bar{a} \times b)\| & =|\bar{a} \times b|=|\sin \phi|\|\bar{a}\|\|b\| \\
& =|\sin \phi|\|a\|\|b\|
\end{aligned}
$$
olarak yazabiliriz. Yukarıdaki eşitsizlikte yerlerine koyarak
$$
\begin{aligned}
\|a \underline{\vee} b\| & \leq(|\cos \phi|+|\sin \phi|)\|a\|\| b\| \\
& \leq \sqrt{2}\|a\|\|b\|
\end{aligned}
$$
sonucunu elde ederiz. $\quad \square$
Eşitsizlikteki $\sqrt{2}$ mümkün olan en küçük çarpandır. Örneğin $a=\mathbf{k}$ ve $b=\mathbf{j}+\mathbf{k}$ alırsak $\|a \underline{\vee} b\|=$ $\sqrt{2}\|a\|\|b\|$ eşitliği sağlanır.
10. Birincil düzlemler
Birincil ekseni içeren düzlemler $v$-çarpımında özel bir yer tutuyor. Bunları birincil düzlemler olarak adlandırıyoruz. $v$-çarpımı bu düzleme kısıtlandığında kompleks sayılarla izomorf bir yapı elde edilir.
Verilen $a$ ve $b$ vektörlerinin aynı birincil düzlemde olması $a, b$ ve $\mathbf{1}$ vektörlerinin lineer bağımlı olmasıyla eşdeğerdir. Bu koşulu da üçlü çarpım kullanarak
$$
\mathbf{1} \cdot(a \times b)=0 \tag{12}
$$
şeklinde ifade edebiliriz. Bu durumda $\bar{a}$ ve $\bar{b}$ de aynı düzlemde olacağı için bu koşul dört değişik şekilde yazllabilir.
Birincil dönmeler “aynı birincil düzlemde olma” özelliğini korur. Bundan yola çıkarak biraz daha genel bir koşul yazılabilir:
Lemma 1. $S$ herhangi bir birincil dönme olsun. $\mathbf{1} \cdot S(a \times b)=0$ eşitliği a ve $b$ vektörlerinin aynı birincil düzlemde olması için gerekli ve yeterlidir.
Kanıt. $S$ iç çarpımları koruduğu ve $S \mathbf{1}=\mathbf{1}$ olduğu için her zaman
$$
\mathbf{1} \cdot(a \times b)=S \mathbf{1} \cdot S(a \times b)=\mathbf{1} \cdot S(a \times b)
$$
eşitliği geçerlidir. $\quad \square$
11. Birincil düzlemlerde $v$-çarpımı
Gözlem 8. Birincil düzlemler $v$-çarpımı altında kapalıdır. (Linear Algebra 1892, s. 19)
Kanıt. Her $a$ için $R a \cdot a=a_{1}^{2}=(\mathbf{1} \cdot a)^{2}$ olduğu tanımlardan kolayca hesaplanır.
$c=a \underline{\vee} b$ olsun. Bunu $(4)$ eşitliğini kullanarak yazalım:
$$
c=(\bar{a} \cdot b) \mathbf{1}-R(\bar{a} \times b)
$$
Her iki tarafın $\bar{a} \times b$ ile iç çarpımını alalım:
$$
\begin{aligned}
c \cdot(\bar{a} \times b) & =(\bar{a} \cdot b) \mathbf{1} \cdot(\bar{a} \times b)-R(\bar{a} \times b) \cdot(\bar{a} \times b) \\
& =(\bar{a} \cdot b) \mathbf{1} \cdot(\bar{a} \times b)-(\mathbf{1} \cdot(\bar{a} \times b))^{2}
\end{aligned}
$$
Eğer $1 \cdot(\bar{a} \times b)=0$ ise $c \cdot(\bar{a} \times b)=0$ olur. Yani $a$ ve $b$ vektörleri aynı birincil düzlemdeyse, $c$ vektörü de aynı düzlemdedir. $\quad \square$
12. Birincil düzlemlerde normun bir özelliği
Gözlem 9. $a$ ve $b$ vektörleri aynı birincil düzlemdeyse
$$
\|a \underline{\vee} b\|=\|a\|\|b\| \tag{13}
$$
eşitliği sağlanır.
Kanıt. Herhangi iki $a$ ve $b$ vektörü için $a \underline{\vee} b$ vektörünün normunu iç çarpım kullanarak yazalım:
$$
\begin{aligned}
\| a \underline{\vee} b \|^{2} & =(a \underline{\vee} b) \cdot(a \underline{\vee} b) \\
& =((\bar{a} \cdot b) \mathbf{1}-R(\bar{a} \times b)) \cdot((\bar{a} \cdot b) \mathbf{1}-R(\bar{a} \times b)) \\
& =(\bar{a} \cdot b)^{2}-2(\bar{a} \cdot b) \mathbf{1} \cdot R(\bar{a} \times b)+\|R(\bar{a} \times b)\|^{2}
\end{aligned}
$$
Eğer $a$ ve $b$ aynı birincil düzlemdeyse Lemma 1 sonucu olarak ortadaki terim sıfır olur ve şu eşitliği elde ederiz:
$$
\begin{aligned}
\|a \underline{\vee} b\|^{2} & =(\bar{a} \cdot b)^{2}+\|\bar{a} \times b\|^{2} \\
& =\cos ^{2} \phi\|\bar{a}\|^{2}\|b\|^{2}+\sin ^{2} \phi\|\bar{a}\|^{2}\|b\|^{2} \\
& =\|\bar{a}\|^{2}\|b\|^{2}\\
& =\|a\|^{2}\|b\|^{2}
\end{aligned}
$$
Dolayısıyla $(13)$ eşitliği sağlanır. $\quad \square$
13. Kuaterniyon çarpımı
Dört boyutta tanımlanan kuaterniyon çarpımı ile iç ve dış çarpım işlemleri arasında da benzer ilişkiler vardır. $x=x_{0}+x_{1} i+x_{2} j+x_{3} k$ olarak yazılan bir kuaterniyon bir reel sayı ile üç boyutlu bir vektörün formel toplamı olarak düşünülebilir: $x=x_{0}+\hat{x}$. Kuaterniyonların çarpımı şu eşitliklerle tanımlanır:
$$
\begin{aligned}
& i^{2}=j^{2}=k^{2}=-1 \\
& i * j=-j * i=k \\
& j * k=-k * j=i \\
& k * i=-i * k=j
\end{aligned}
$$
İki kuaterniyonun çarpımı vektör kısımlarının iç ve dış çarpımı kullanılarak şu şekilde yazılabilir (Gürlebeck ve Sprössig 1997):
$$
x * y=x_{0} y_{0}-\hat{x} \cdot \hat{y}+x_{0} \hat{y}+y_{0} \hat{x}+\hat{x} \times \hat{y}
$$
Reel kısmı sıfır olan kuaterniyonlara saf kuaterniyon adı veriliyor. Saf kuaterniyonlar için yukarıdaki ifade şu şekli alır:
$$
x * y=-x \cdot y+x \times y
$$
Yine saf kuaterniyonların iç ve dış çarpımları kuaterniyon çarpımı cinsinden şu şekilde yazılabilir:
$$
\begin{aligned}
x \cdot y & =-\frac{1}{2}(x * y+y * x) \\
x \times y & =\frac{1}{2}(x * y-y * x)
\end{aligned}
$$
14. Sonuç
Günümüzde üç boyutlu vektör analizinde iç ve dış çarpımların doğal bir yeri vardır. Bu çarpımlara $R$ “birincil” dönmesini de ekleyerek bir “kavramsal çerçeve” oluşturduk. Bu çerçeve sayesinde Linear Algebra kitabındaki bazı neticeleri bu terimler cinsinden daha basit bir şekilde elde ettik. Tüm gözlemlerimizi bu yazıya sığdıramadık. Bir neticenin yanında kitaptan bir sayfa numarasının olmadığı durumlar o neticeyi kitapta bulamadığımız içindir. Bu durumlarda neticemizin yeni olduğunu tahmin ediyoruz. Vidinli çarpımının analitik geometri neticeleri elde etmekte etkin olmasinin en önemli sebebinin iç ve dış çarpımın Vidinli çarpımı cinsinden ifade edilebilmesi olabilir. Benzer bir kuramsal çerçeve kuaterniyonlar için de bilinmektedir. Yani üç boyutta Vidinli çarpımı dört boyutta kuaterniyon çarpımı cinsinden ifade edilebiliyor. İki çarpımla ilgili bu kuvvetli ilişkilerin kitabın teknik değerlendirmelerine katkı sağlamasını temenni ediyoruz.
Teşekkür. Çalışmamız sırasında bizi devamlı olarak yüreklendiren Şahin Koçak’a ne kadar teşekkür etsek azdır. Atilla Polat, Semiha Betül Takıcak Bayam ve Sadık Değer’e de katkılarından dolayı teşekkür ederiz.
Kaynakça:
- Crowe, Michael J. (1994) A History of Vector Analysis: The Evolution of the Idea of a Vectorial System, Dover.
- Çeçen, Kazım (1988) Hüseyin Tevfik Paşa ve “Linear Algebra”, İTÜ Bilim ve Teknik Tarihi Araştırma Merkezi Yayın No. 5, 1988, İstanbul. (İkinci baskı 2019)
- Gürlebeck, Klaus; Sprössig, Wolfgang (1997) Quaternionic and Clifford calculus for physicists and engineers, Mathematical methods in practice, vol. 1, Wiley.
- Husseïn Tevfik Pacha (1882) Linear Algebra, 69 sayfa, Constantinople, Press of A. H. Boyajian. (Çeçen 1988 içinde vardir.)
- Husseïn Tevfik Pacha (1892) Linear Algebra, Second Edition, Revised and Enlarged, 187 sayfa, Constantinople, Press of A. H. Boyajian. (Çeçen 1988 içinde vardır.)
- Marsden, Jerrold; Tromba, Anthony (2012) Vector calculus, 6th ed., New York, W.H. Freeman.
- Polat, Atilla (2019) “Son Dönem Osmanlı MatematikçiBürokratı Vidinli Hüseyin Tevfik Paşa’nın hayatı”, Osmanlı Bilimi Araştırmaları 20, 1, s. 16-46.
- Tait, Peter Guthrie (1867) Quaternions, 320 sayfa, Clarendon Press, London, Macmillan and Co.
- Tezer, Cem (2015) “Vidinli Hüseyin Tevfik Paşa (d. 1832 ö. 1901)”, Tanzimat’tan Günümüze Türk Düşüncesi, C. 3, ed. Süleyman Hayri Bolay, Ankara: Nobel Akademik Yayıncllık içinde, s. 1415-1429.
- Schubring, Gert (2007) “Hüseyin Tevfik Pasha – the Inventor of ‘Linear Algebra'”, Osmanlı Bilimi Araştırmaları 8, s. $43-48$.

