Yazar: Ahmet Feyzioğlu (feyziogl@boun.edu.tr)
Yıl: 2022-4
Sayı: 114
Öklid’in yaklaşık M.Ö. 323–285 yılları arasında yaşadı. İskenderiye’de çalıştı. Elemanlar kitabı, en ünlü ve en önemli eseridir. Bu kitap hemen hemen bütün dünya dillerine çevrilmiş ve yüzyıllar boyunca okullarda okutulagelmiştir. Hüseyin Rıfkı Tamani tarafından 1797 yılında %40’a yakın bir kısmı Usûl-i Hendese adıyla Osmanlıcaya çevrilmiştir. Modern Türkçeye çevrilmiş kısımları da vardır [ÖE, vi–viii].
Elemanlar on üç kitaptan oluşur. Her kitabın başında, o kitapta kullanılacak tanımlar, doğru kabul edilecek belitler (aksiyomlar) açıklanır. Bundan sonra önermelere geçilir, tanım ve belitlerden başka bir şey kullanmaksızın önermeler ispat edilir, daha doğrusu ispat edilmeye çalışılır. Yıllar boyunca didik didik edilen Elemanlar ’da eksiklikler görüldü, bazı tanımların yeterli olmadığı saptandı, kullanılacağı açıkça söylenmemiş belit ve önermelerin kullanıldığı fark edildi. Öklid geometrisinin eksiklilerden arındırılmış hali David Hilbert’in (1862–1943) 1899 yılında yayınladığı Grundlagen der Geometry kitabında bulunur. Eksiklikleri olmakla beraber, Elemanlar temel tanım ve belitler üzerine inşa edilen bir matematik abidesidir ve belitsel yapısıyla bir ideal olmuştur. Birçok bilim dalına örnek olmuştur.
Elemanlar geometri kitabıdır, evet, ama yalnızca geometri kitabı değil. Geometri nedir? Kadim Yunan’da geometri bütün matematiğin temeliydi. Elemanlar da o dönemin bütün matematiğinin sistemleştirilmiş halidir. Bugün bizim temel cebirsel özdeşlikler, sayılar teorisi, gerçek sayıların kuruluşu diye adlandıracağımız konular da Elemanlar’da işlenir.
“Yaklaşık 2300 yıl önce yazılmış bir kitaptan ne öğrenebiliriz ki? O kitapta lise matematiğinden başka ne olabilir ki?” gibi düşünceler aklımıza gelirse, önce şu soruları cevaplandırmamız yerinde olur.
• $\cos 24^\circ$’nin (ondalık açılımını değil) tam değerini kareköklü ifadelerle bulunuz.
• Bir koninin hacminin, tabanı ve yüksekliği aynı olan silindirin hacminin 1/3’ü olduğunu ispat ediniz.
• Köşeleri, yarıçapı $r$ olan bir küre üzerinde bulunan yirmiyüzlünün kenar uzunluğunu hesaplayınız. Onikiyüzlünün de.
Bu sorulara denk konular Elemanlar ’da ele alınmış, cevapları verilmiştir. Görülüyor ki 2300 yıllık Elemanlar, belitsel yöntemin yerleşmesinde ve yaygınlaşmasında oynadığı önemli rolün yanısıra, ilginç matematik olgularla dolu, tazeliğini hâlâ koruyan, çalışılmaya değer bir eserdir. Ama Elemanlar’ı incelemek isteyen insanımızın önünde bir engel vardı: Elemanlar Türkçeye çevrilmemişti. Üzerimize yapışmış bu ayıbı gidermeye çalışan teşebbüsler olmuşsa da, ayıbı üzerimizden kaldıran kişi Elemanlar’ın tamamını Türkçeye kazandıran meslektaşımız Ali Sinan Sertöz olmuştur.
Sertöz, Elemanlar’ın Türkçeye çevirisini Öklid’in Elemanları adıyla yayınladı. Tübitak popüler bilim kitapları dizisi çerçevesinde 2019 yılında ilk basımı yapılan kitap xiii+691 sayfadır. Çevirinin kendisi 684 sayfa tutuyor. Sertöz, Heath’in İngilizce çevirisinin yanısıra başka kaynaklar da kullanmıştır [ÖE, vi–vii]. Her sayfada 25–30 satır vardır.
Sayfaların antetlerinde kitap ve önerme sayılarının olması okuyucunun işini kolaylaştırıyor. Satırların arası ferah, harflerin puntosu büyük, yazıların okuması rahattır. TikZ ile çizilmiş şekilleri gayet kalitelidir. Kısaca tanıttığımız şu dış özelliklerinden bile Öklid’in Elemanları’nın büyük emeklerle vücuda getirildiği belli oluyor. Tercümeye verilen emek hakkında fikir sahibi olmaya çalışalım. Elemanlar ’ın bazı önermeleri uzun mu uzundur. Böyle uzun cümleleri başka bir dile hakkıyla çevirmek kolay iş değildir. Tabi uzun cümleleri parçalara bölmek ve değiştirmek söz konusu olamaz, çünkü böyle yapmak tercüme değil sadeleştirme ve açıklama yapmak olur. Oysa Elemanlar gibi tarihi bir eserin iyi tercümesi, okumaları sırasında nasıl çalışmış, nasıl yorulmuş, nasıl lezzet almışsa, tercümeyi okuyanın zihni de aynı şekilde çalışacak, aynı şekilde yorulacak ve aynı lezzeti alacak. Başka bir deyişle, çeviriyi okuyan, kitabın aslını okuyanın haline bürünecek. Örneğin bugün “$a$ tamsayısı $b$ tamsayısını böler” diye ifade ettiğimiz durumu, Öklid’in diliyle ifade etmek, mesela “$AX$ $BY$’yi ölçer” diye çevirmek gerekir ki $AX$ doğru parçası ölçü birimi olarak alınırsa $BY$ tam tamına $AX$’in bir tamsayı katıdır demektir. “Böler” diye tercüme edilse, Elemanlar‘a tamamiyle hakim olan geometrik atmosfer bozulmuş olur.
Çeviri yapmanın zorluğunu hissedebilmemiz için bir örnek verelim, Elemanlar‘ın dokuzuncu kitabındaki 35 numaralı önermeyi Heath’in eski$^1$ İngilizceyle ifade ettiği şekilde yazalım [Heath, II. 420]:
“If as many numbers as we please be in continued proportion, and there be subtracted from the second and the last numbers equal to the third, then, as the excess of the second is to the first, so will the excess of the last be to all those before it.”
İngilizce bilen okuyucularımızı bu önermeyi Türkçeye çevirmeye davet ediyorum.
Sertöz’ün gayet başarılı olan çevirisini Öklid’in Elemanları‘nın 326. sayfasında bulabilirsiniz. Kendisinin çeviriyi büyük bir özen ile hazırladığı anlaşılıyor. (Bu arada parantez içinde söyleyelim, bu önerme temel bir toplam formülünün Öklidce yazılışıdır. Hangi formülün? Eh, 326. sayfaya bakınız.)
Öklid’in Elemanları‘nı okumaya geçelim, böylece Elemanlar‘ın içeriği hakkında biraz malumat da edinelim.
Öklid’in Elemanlar’ı ve Öklid’in Elemanları
Birinci kitap
Birinci kitap, Elemanlar‘ın en çok tercüme edilen, en çok incelenen, en çok tartışılan kitabıdır. Kitap tanımlar, belitler (postülat) ve ortak kavramlar ile başlar. Postülat ile aksiyom arasındaki farkın ne olduğu tarih boyunca tartışılagelmiştir. Öklid’in ilk üç beliti, birtakım inşaların mümkün olduğunu söyler, örneğin 2. belit Bir doğru istenildiği kadar yine bir doğru olacak şekilde uzatılabilir der. Bu belit geometrik bir inşa da olabilir, düzlemin homojen olduğu şeklinde bir mekan felsefesi iddiası da. Belitlerin en önemlisi ve tartışılanı 5. belittir: Eğer bir doğru iki doğruyu kestiğinde bu doğrunun aynı tarafındaki iç açılar iki dik açıdan küçükse bu iki doğru o yönde uzatıldıklarında kesişir. Matematikçiler tarih boyunca, ifadesi uzun ve karışık olan bu 5. beliti, tanımlar diğer belitler ve ortak kavramları kullanarak ispat etmeye, onu belit olmaktan çıkarıp önerme yapmaya çalıştılar. Başaramadılar. Bu faaliyetler, Öklid dışı geometrinin keşfine yol açtı. Ortak kavram ile belit arasındaki fark da bariz değildir. Ortak kavram, bütün nicelikler için geçerli belitler gibi gözüküyor.
Birinci kitabın içeriğinden daha önemlisi, geometriyi tarihte ilk kez sistemli bir belitsel çerçevede sunmuş olmasıdır.
İçeriğine geçelim. Birinci kitap, klasik düzlem geometrisinin temelini anlatır. İlk 26 önerme, üçgenler ve kongrüans hakkında en temel teoremlerdir, bunların ispatında 5. belitin kullanılmadığı dikkati çeker. Bunları takip eden 27.-32. önermeler, üçgende açılar toplamı ile ilgilidir. Sonraki 33.-46. önermeler, özdeş parçalardan oluşan ama kendileri özdeş olmayan şekillerin kuruluşunu ele alır. Kitap Pisagor teoreminin ve tersinin ispatıyla zirveye çıkar ve orada sona erer.
İkinci kitap
İkinci kitap, cebirin temel özdeşliklerini ele alır, bugünkü notasyonumuzla
$$\begin{split} a(b+c+d+\cdots) & = ab + ac+ ad+\cdots\\
ab+a(a-b) &= a^2 \\
a^2+b^2 &= 2ab +(a-b)^2\end{split}$$
yazacaklarımız gibi birçok özdeşliği ispat eder. Ama ikinci kitabın asıl amacı geometri kılığı altında cebir yapmak değildir. Pisagor teoremi aracılığıyla $\sqrt{a^2 + b^2}$, $\sqrt{a^2\, -\, b^2}$ ifadeleriyle alan hesaplamaları yapılır, kuadratik denklemlerin çözümü bulunur ve ele alınan bir dikdörtgenle aynı alana sahip olan kare inşa edilir. Böylece alanın kareler aracılığıyla ifade edilmesi mümkün olur. Bugün alan için metre kare gibi birimler kullanıyorsak, bunun teorik temeli ikinci kitapta atılmıştır.
Vektör hesabında temel rolü olan bir trigonometri özdeşliği, ikinci kitapta geometri kılığında ifadesini bulur. Bu özdeşliği iki ayrı halde iki ayrı şekilde ifade eden önermeleri okuyalım.
Önerme 1 (II. Kitap, 12. Önerme) Geniş açılı bir üçgende geniş açıyı gören kenar üzerindeki kare, diğer kenarlar üzerindeki karelerin toplamından bu kenarlardan biriyle o kenarın diğer köşeden gelen dikmeyle birleşinceye kadar uzatan doğrunun içerdiği dikdörtgenin iki katı kadar büyüktür.
Önerme 2 (II. Kitap, 13. Önerme) Dar açılı üçgenlerde, dar açıyı gören kenar üzerindeki kare, dar açıyı içine alan kenarlar üzerindeki karelerin toplamından dar açı etrafındaki kenarlardan biriyle yani üzerine dikme indirileni ile dikmenin ayağıyla dar açılı köşe arasındaki doğru tarafından içerilen dikdörtgenin iki kat kadar küçüktür.
Bu önermeler size tanıdık geldi mi? Gelmediyse önermeleri anlatan bir resim çizin. Gene tanıdık gelmiyorlarsa Öklid’in Elemanları‘nda 68.-69. sayfaları okuyun.
Üçüncü kitap
Üçüncü kitap, çemberi ele alır, çember parçalarını, yayları ve açıları inceler.
Dördüncü kitap
Dördüncü kitap, şekillerin iççemberlerinden ve dışçemberlerinden bahseder. Çemberbölüm konusundaki en önemli ciddi adımları bu kitapta buluyoruz. Düzgün beşgenin çizimi yapılır. Kitap düzgün 15genin inşa edilmesiyle son bulur.
Düzgün 15genin çizimi, $\cos 24^\circ$ uzunluğunda doğru parçası çizmeye denktir. Rica ediyorum $\cos 24^\circ$’yi tamsayılarla ve yalnızca toplama, çıkarma, çarpma, bölme ve karekök alma işaretleriyle yazar mısınız?
Dördüncü kitabın son önermesini, 16. önermesini okuyalım.
Önerme 3 (IV. Kitap, 16. Önerme) Verilen bir çemberin içine, hem eşkenar hem de eş açılı olacak on beş açılı bir şekil çizmenin yolu.
Evet, düzgün 15geni inşa etmenin yolu Öklid’in Elemanları‘nın 143. sayfasında meraklılarını bekliyor.
Beşinci kitap
Beşinci kitap, aynı türden niceliklerin oranları hakkındadır. Bu kitabın içeriği Eudoxus’a (M.Ö. 395/390 – 342/337) aittir. Elemanların VI.–XIII. kitaplarında kullanılacak olan temel oran kavramı beşinci kitapta hazırlanır. İşe eşitsizliklerle başlanır. Nicelikler doğru parçalarıyla temsil edilirler. Ancak genelliği bozmamak için doğru parçaları yan yana veya alt alta çizilmişlerdir, bireydirler; bir araya gelip geometrik bir şekil oluşturmazlar, çünkü konu geometrik şekiller değil, soyut ve genel oran kavramıdır.
Beşinci kitabın en önemli tanımlarından birini Sertöz’ün çevirisiyle okuyalım.
Tanım 1 (V. Kitap, 5. Tanım) Nicelikler, eğer birinciyle üçüncünün herhangi eşit katları ikinciyle dördüncünün herhangi eşit katlarından sırasıyla aynı anda büyük, aynı anda eşit ya da aynı anda küçük olursa aynı orandadır denir, yani birinci ikinciye ve üçüncü dördüncüye.
Bence mükemmel bir çeviri. Tanımı olduğu gibi veren, açıklama kısaltma uzatma yapmayan bir çeviri. Bu tanımı ilk okuyuşumuzda hemen anlamayabiliriz. Zaten öyle olması gerekir! Sertöz böyle durumlarda yardımcı olmakta, tercümenin dışına açıklayıcı notlar eklemekte, okuyucunun işini kolaylaştırmaktadır. Yukarıdaki tanımın açıklaması şöyledir:
$\big[$ $a$, $b$, $c$, $d$ nicelikleri verildiğinde eğer her $m$, $n$ tamsayıları için aşağıdaki üç durumdan mutlaka biri gerçekleşiyorsa
$$\begin{split} 1)\, ma &> nb \text{ ve } mc > nd,\\ 2)\, ma &= nb \text{ ve } mc = nd, \\ 3)\, ma &< nb \text{ ve } mc < nd; \end{split}$$ bu durumda $a : b :: c : d$ yani $\dfrac{a}{b} = \dfrac{c}{d}$ deriz. $\dots\big]$
Eudoxus’un yukarıdaki tanımı o kadar genel, o kadar iyi hazırlanmıştır ki, 19. yüzyılın sonlarına doğru gerçek sayıların inşası için Richard Dedekind’in (1831–1916) kurduğu “kesit” kavramına da ilham olmuştur. Hatta kesit teorisi Eudoxus’un oran teorisiyle ilk bakışta neredeyse aynıdır. Nitekim Rudolf Lipschitz (1832–1903) Dedekind’e 6 Haziran 1876 tarihinde yazdığı mektupta “Öklid tarafından verilen (V. 5) tanımını, sizin tanımınız kadar tatmin edici bulduğumu söyleyebilirim” diyor [Dedekind, 469] ve “[Gerçek sayılar kümesinin] tamlığı hakkında bahsettiğiniz ve ana ilkelerinizden çıkarsadığınız şey, esasında çizginin temel niteliği ile örtüşmektedir ki bu temel nitelik olmaksızın kimse çizgiyi tasavvur edemez” diye ekliyordu [Dedekind, 475]. Aslında Lipschitz haksızdı. Önceki yüzyıllarda olduğu gibi matematiğin temellerini sezgisel olarak anlamanın yeterli olduğu kanaatini sürdürmekteydi. Oysa Dedekind yeni bir çağ, yeni bir çığır başlatanlardandı: temeller tasavvurlara değil sarih ve mantıksal ifadeler üzerine oturtulacaktır. Gene de Eudoxus’un oran teorisinin tazeliğinden hiç bir şey yitirmemiş olması dikkate değer ve hayranlığımızı celb eder.
Altıncı kitap
Altıncı kitap, benzerlik teorisini işler. Beşinci kitapta en genel ve en soyut şekilde işlenmiş olan oran teorisi, altıncı kitapta geometrik şekillere uygulanır ve benzer şekiller teorisi kurulur. Bir örnek verelim.
Önerme 4 (VI. Kitap, 28. Önerme) Bir doğru üzerine verilen bir düzkenar şekle eşit ve verilen bir paralelkenara benzer bir paralelkenar kadar tümden eksik bir paralelkenar çizmenin yolu; böylece verilen düzkenar şekil verilen paralelkenara benzer ve doğrunun yarısı üzerine çizilen paralelkenardan büyük olmamalıdır.
Eğer AB doğrusu, C düzkenar şekli, D paralelkenarı verilmişse,
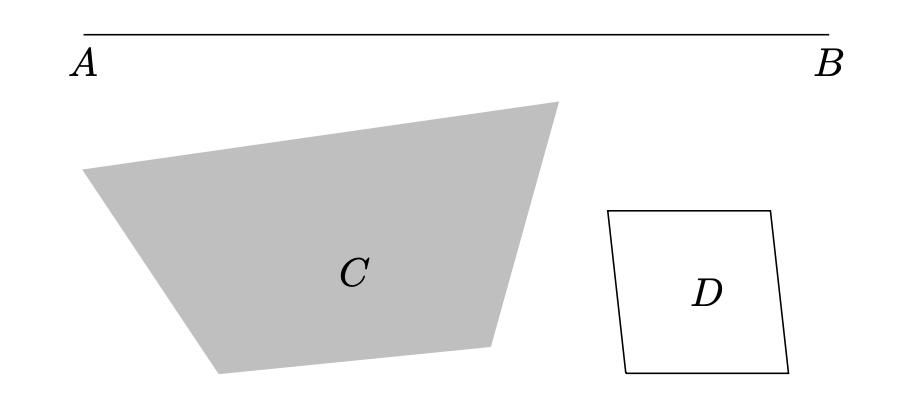
$AB$’nin bir kısmı üzerinde öyle bir $ATQS$ paralelkenarı kuracağız ki, alanı $C$’nin alanına eşit olacak, $AB$ doğrusu üzerinde kalmayan $SQRB$ parçası verilen $D$’ye benzer olacak.

Bu geometrik inşa, cebirsel olarak ifade edilince çok daha kolaylaşıyor (onuncu kitap hakkında yazdıklarımıza bakınız). Yapılacak olan şey, $AB$’nin uzunluğuna $a$, ve $D$’nin tabanı ile yüksekliğine $b$ ile $c$, ve $C$’nin alanına $S$ demek ve $x(a – \frac{b}{c}x) = S$ denklemini çözmektir; denklemin gerçek bir kökünün var olabilmesi için gerekli şart olan $S \leq \frac{a}{2} \cdot (\frac{c}{b} \cdot \frac{a}{2})$ eşitsizliği, önermede belirtilmiştir.
Yedinci kitap
Yedinci kitap, sayılar teorisine giriş mahiyetindedir. En büyük ortak bölen tanımı, Öklid algoritması, Öklid’in yardımcı teoremi bu kitapta yer alır.
İki pozitif tamsayının aralarında asal olup olmadıklarını nasıl bulunur? Bir algoritma ile. Bu algoritma bilgisayara girdi olarak verilecek sembollerden oluşur, mesela şöyle [MSD, 244]:
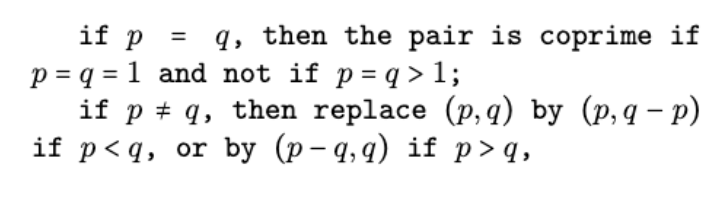
Yani, $p$, $q$ pozitif tamsayıları verildiğinde,

Şimdi burada aklımıza bir soru geliyor. “Bu algoritmayı yani sembollerle yapılan işlem dizisini, matematiğin tamamını geometriye indirgemiş kadim Yunanlılar nasıl uygulayabilirler ki? Algoritma nerede, geometri nerede?” Bu sorunun cevabını yedinci kitabın birinci önermesinde buluyoruz. Okuyalım.
Önerme 5 (VII. Kitap, 1. Önerme) Eşit olmayan iki sayı, sürekli olarak sırasıyla küçük olan büyük olandan çıkarıldığında, eğer birim kalana kadar hiçbir kalan sayı bir öncekini ölçmüyorsa ilk sayılar aralarında asal olacaktır.
Kısacası, bu önerme yukarıdaki algoritmadan başka bir şey değildir! Veyahut, yukarıdaki algoritma Elemanlar‘ın bir önermesidir!
Önermenin geometrik kılıktaki ispatını Öklid’in Elemanları‘nda 223. sayfada bulacaksınız.
Yedinci kitapta çarpma işleminin değişmeli olduğunun ispatı da vardır, ilginizi çekebilir (16. önerme, [ÖE, 238].
Yedinci kitabı okumaya devam edelim ve 30. önermeye gelelim [ÖE, 250].
Önerme 6 (VII. Kitap, 30. Önerme) Eğer iki sayı birbirine çarparak bir sayı oluşturursa ve bir asal sayı bu çarpımı ölçerse baştaki sayılardan birini de ölçer.
Bugünkü matematik diliyle söyleyecek olursak: eğer $p$, $a$, $b$ pozitif tamsayılar ve $p$ asalsa, ve $p \mid ab$ ise, o zaman $p \mid a$ veya $p \mid b$’dir. “Öklid’in yardımcı teoremi” diye bilinen bu önerme, aritmetiğin temel teoreminin ispatında can alıcı bir rol oynar. Öklid’in ispatı, bugün modern sayılar teorisi kitaplarında bulunan (ve $p \nmid a$ ise $ax + py = 1$ olacak şekilde $x$ ve $y$ tamsayılarının varlığını kullanan) ispatlardan farklıdır [ÖE, 250].
Sekizinci kitap
Sekizinci kitap, yine oranlar teorisi üzerine kurulmuştur. Geometrik dizilerin terimleri arasındaki ilişkileri araştırır.
Dokuzuncu kitap
Dokuzuncu kitap, asal sayıları konu edinir. Sonsuz miktarda asal sayı bulunduğu teoremi bu kitapta ispatlanır. Bir tamsayının mükemmel tamsayı olması için yeterli bir şart verilerek kitap kapanır.
Önerme 7 (IX. Kitap, 20. Önerme) Asal sayıların miktarı, seçilen her asal sayı topluluğunun miktarından fazladır.
Öklid’in ispatı, verilen her asal listesinin dışında bir asal sayı kurmaya dayanır. Sertöz bu önemli noktayı vurguluyor:
“Asalların sonsuz olduğunu kanıtı. Öklid, asalların sonlu olduğunu kabul edip bundan bir çelişki çıkararak kanıtlamaz asalların sonsuz olduğunu; sonlu sayıda asal seçersek, bunların dışında bir asal daha olacağını gösterir.”
Onuncu kitap
Onuncu kitap pergel ve cetvel ile çizilebilen irrasyonel sayılar hakkındadır. Ard arda iki kuadratik denklemin çözümüyle elde edilebilecek sayılar incelenir. Elemanlar‘ın kitapları içinde en zor ve en uzun olanıdır. Öklid’in Elemanları‘nın dörtte birinden daha fazla sayfa tutar. Kitabın bir kısmı Theaetetus’un (M.Ö. 417–369) çalışmalarını anlatır.
Kadim Yunan matematikçileri, eşölçeksiz$^2$ niceliklerin yaklaşık değerlerini kullanmak yerine, çalışmalarına onları oldukları gibi dahil ettiler, tıpkı bizim $1.412\dots$, $3.141\dots$ yerine $\sqrt 2$, $\pi$ yazmamız gibi. Biz farklı nicelikleri $\sqrt 2$, $\sqrt 3$, $\sqrt 5$ gibi farklı sembollerle temsil edebiliyoruz, onlar sembollerle değil doğru parçalarıyla temsil ettikleri için ve doğru parçaları da hep birbirine benzediği için, örneğin $\sqrt 2 + \sqrt 3$ ile $\sqrt 5 – \sqrt 3$ arasındaki farkı ancak bu niceliklerin inşasını takip ederek koruyabildiler. Bu yüzden nicelikleri inşalarına göre sınıflandırdılar ve birçok sınıf icat ettiler. Sertöz’ün çevirisi şöyledir.
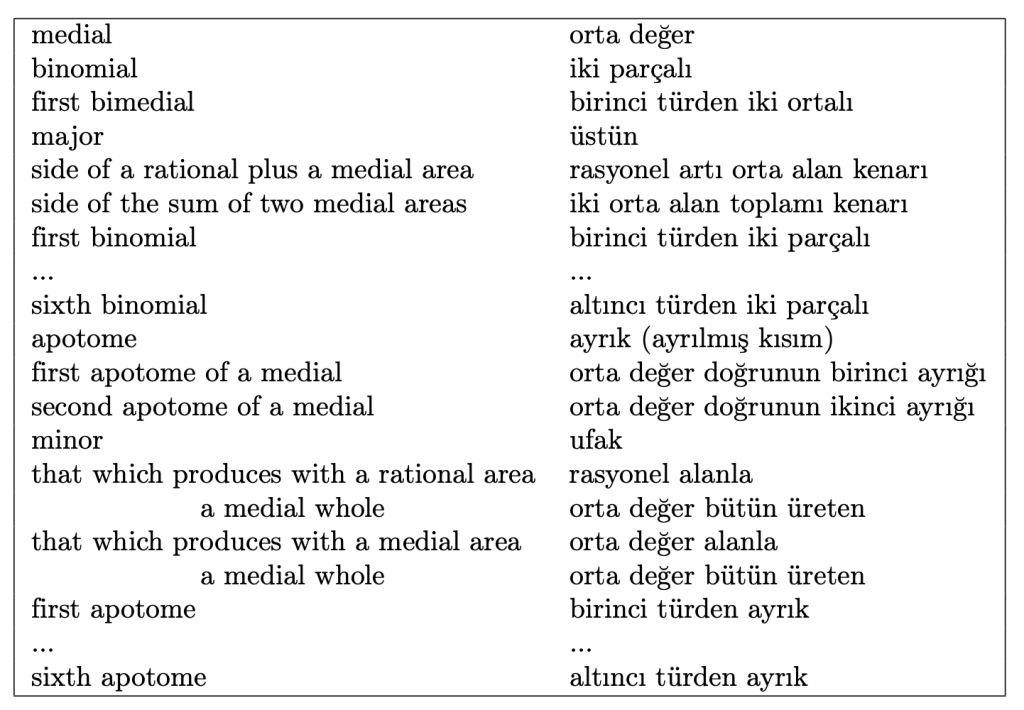
Bu terminoloji kalabalıklığı sonunda hantal bir teoriye yol açtı. Zor anlaşılır bir teoriye. Benedetto Castelli (1578–1643) bile 1 Nisan 1607 tarihini taşıyan bir mektubunda Galileo Galilei’ye (1564–1642) “terimlerin çokluğunda, sınıflamaların derinliğinde, ispatların güçlüğünde boğuldum” deyip onuncu kitabın 40. önermesinde takılıp kaldığından şikayet eder (Cantor’dan naklen) [Cantor, 254]. Bütün bu eşölçeksiz nicelikler, bizim kolaylıkla $\sqrt{a \sqrt{b}}$, $\sqrt{\frac{a^2 + a \sqrt{b}} {2}}$, $\sqrt{\frac{(\sqrt a + \sqrt b) \sqrt{a – b}}{2}}$ gibi sembollerle yazabileceğimiz niceliklerdir.
Peki bu hantal mı hantal teoriye niçin ihtiyaç var? Yanıt: $\sqrt{10(5 – \sqrt{5})}$ gibi büyüklüklerin inşa edilebilmesi için.
Bugün $\sqrt{10(5 – \sqrt{5})}$ gibi ifadelerle nasıl çalışabiliz? Gerçek sayılar kümesinin elemanları olarak ele alabiliriz, ama o zaman önceden gerçek sayıları kurmak gerekir—az iş değil. “Belirsizler” diye düşünebiliriz, ama o zaman cebirsel kapanış gibi kavramlara müracat etmek gerekir—o da az iş değil. Theaetetus ve diğerleri de onuncu kitaptaki teoriyi kurmuşlar—az iş olmaması şaşırtıcı değil.
Kadim matematikçilerde yapacakları iş için uygun aletler yoktu, sadece geometrik aletler vardı, onlarla akıl yürütmek de sakil mi sakildi. Oysa sembol ve harflerle akıl yürütüldüğünde teoremlerin ispatı hayret verici ölçüde basitleşiyor.
Onuncu kitabı okurken kadim Yunan matematikçilerine acımak ile hayran olmak arasında bocalıyoruz. Acıyoruz çünkü kurdukları teorileri geometrik şekillerle ifade etmeleri onları büyük sıkışıklığa itmiş ve labirent gibi teoriler kurmaya zorlanmıştır, hayran oluyoruz çünkü o labirentte yollarını şaşırmayıp hedefledikleri teoremleri ispat etmeyi başarmışlardır. Sembol kullanmamaları onların en büyük handikapıydı.
Matematikte nicelikleri sembollerle göstermek ancak 16. ve 17. yüzyılda kabul görmeye başladı. Bunun basit bir değişiklik olduğu zannedilmesin. Sembollerle işlem yapan kişiler şiddetli tenkitlere maruz kalmışlardır. Bakınız sembollerle yazan John Wallis’e (1616–1703) Pierre de Fermat (1607–1665) neler diyor [Fermat, 475]
“Son olarak, mektuplaştığımız seçkin beyleri, bir süreliğine de olsa, analitik aletleri$^3$ kenara kaldırmaya ve geometri problemlerini Öklid ile Apollonius’un metoduyla ele almayı salık veririz, zira arzu edilir ki ispat ve inşalarda kadim matematikçilerin her şeyden önce hedeflediği zerafetin yavaş yavaş kaybolduğuna tanık olmayalım.”
Matematiksel argümanı geometrik şekiller yerine semboller ve harfler üzerine kurmak “matematiğin aritmetikleş(tiril)mesi” diye bilinir. On yedinci yüzyılda başlayan bu paradigma değişikliği hala da devam etmektedir. Dedekind–Lipschitz mektuplaşması da aritmetikleştirme taraftarı ile karşıtının tartışması olarak karşımıza çıkıyor.
Aritmetikleştirme olmasaydı, $$\int_0^a x^2 \, dx = \frac{1}{3}a^3$$ yerine “Exposito parallelogrammo quocunque in eoque ducta diametro; omnia quadrata parallalogrammi ad omnia quadrata cuiusvis triangulorum per dictam diametrum constitutorum erunt in ratione tripla, uno laterum parallalogrammi communi regula existente” gibi uzun cümleler yazmaya mecbur kalır [Kirsti, 323], — bırakın türevsel denklemleri kurmayı ve çözmeyi — diferansiyel ve integral hesabı kuramaz, 17. yüzyıldan sonraki bilimsel gelişmelerden ve uygulamalarından habersiz ve yoksun yaşardık.
Sembollerin kullanılmasının ne denli rahatlık sağladığını 21. yüzyılda hakkıyla anlayamıyoruz. Öklid’in onuncu kitabını incelemek, farkında olmadığımız bu nimetin kıymeti hakkında biraz fikir sahibi olmamıza yarayacaktır.
Öklid’in Elemanları‘nı okumak ne kadar öğretici ve düşündürücü.
On birinci kitap
On birinci kitap ile Elemanlar, uzay geometrisine geçer. Doğru ve düzlemlerin dikliği ve paralelliği ele alınır. Paralelyüzlüler ve prizmalar bu kitapta incelenir.
On ikinci kitap
On ikinci kitap cisimlerin hacimlerini konu edinir. İntegral hesabın temelinde yatan “tüketme” metodu anlatılır. “Tüketme” metodunun ilk uygulamasını on ikinci kitabın hemen başında buluyoruz [ÖE, 585].
Önerme 8 [XII. Kitap, 2. Önerme]
Dairelerin birbirine oranı çapları üzerindeki karelerin oranına eşittir.
Çemberin içine düzgün çokgenler çizerek ve adım adım çokgenlerin kenar sayısını iki katına çıkararak, daireyi çokgenlerle tüketebiliriz. On ikinci kitap boyunca aynı “tüketme” metodu üçgen tabanlı piramitlere, çokgen tabanlı piramitlere ve konilere de uygulanacak, piramit ve koniler ile prizma ve silindirlerin hacimleri karşılaştırılacaktır. On ikinci kitap, integral hesabın doğuşunu öğrenmek isteyenler için önemli bir kaynaktır.
On üçüncü kitap
On üçüncü kitap platonik cisimlerin yani düzgün çokyüzlülerin inşasını ele alır.
Yarıçapı $r$ olan bir küre için çizilmiş yirmiyüzlünün kenar uzunluğu kaç birimdir? Ya onikiyüzlünün?
Bu sorularla ilgilenmek isteyenler, Öklid’in Elemanları‘nda on üçüncü kitabın sayfalarını bir karıştırsınlar, bilhassa 16. ve 17. önermeleri okusunlar.
Bilim ve Teknik dergisinden
“Başlarken” adını taşıyan önsözün dışında Öklid’in Elemanları‘da yalnızca Elemanlar‘ı buluyor ve okuyoruz. Sertöz, Elemanlar‘ın matematik ve matematik tarihi için taşıdığı önem hakkında önsözde birkaç söz etmişse de Elemanlar‘ı tarihi perspektifine oturtmayı 2018 yılında Bilim ve Teknik dergisinde çıkan üç yazısına bırakmış [Sertöz 1], [Sertöz 3], [Sertöz 4]. Bu yazılar Öklid’in Elemanları kitabının kılavuzları ve ayrılmaz parçalarıdır, yalnızca beraber ciltlenmemişlerdir.
Bu yazılarla Öklid’i ve Elemanlar‘ı daha iyi tanıyacaksınız, matematik tarihinden bilgiler elde edeceksiniz. Sertöz Öklid’in Elemanları‘nın nasıl okunması gerekliğini de anlatır. Ancak bunlardan önemlisi, Sertöz’ün çeviriyi yaparken ve Öklid’i okurken duyduğu heyecanı ve hazzı bizlerle paylaşmasıdır. Diyor ki [Sertöz 1, 23]:
“Binlerce yıl Batı ve Doğu medeniyetlerini eşit derecede etkilemiş olan Elemanlar kitabı sadece bir matematik kitabı değildir. Gerçeği açığa çıkarma çabasının ciddiyetini ve bunda gizli olan mutluluğu yakalayan, okuyucuda da bir an bu mutluluğu yakaladığı hissini uyandıran bir kitaptır. $\dots$ Bu dünyaya ait ama bambaşka dünyaların rüzgârını estiren bir kitaptır Elemanlar.”
Bu satırların yazarı da aynı heyecan ve hazzın okuyuculara bulaşmasını diler.
Öneriler
İnternette Öklid’in Elemanları‘nın dördüncü sürümünün çıktığı haberini alıyor ve memnun oluyoruz. Gönül ister ki Öklid’in Elemanları çok kişi tarafından okunsun ve yeni yeni baskıları olsun. Sertöz, yeni sürümlerin, Hüseyin Rıfkı Tamani’nin Usûl-i Hendese‘sinin tamamlanışının yıldönümü olan 23 Eylül gününde olmasını tercih ve ilan ederek, hasret kaldığımız bir kıymetbilirlik ve vefadarlık örneği de sergilemiştir. İlerideki sürümlerde göz önüne alınmasını arzu ettiğimiz birkaç şey önerelim.
Sayfaların marjlarında ispatları açıklayan şekiller görüyoruz. Ancak bunlar sayfa gövdesindeki şekillerden daha küçük ölçekte, çizgileri silik, harfleri minik. İlerideki baskılarda bunların daha görünür hale gelmesini dileriz. Ölçeklerini değiştirmeyi veya bütün sayfa düzenini değiştirmeyi öneremeyiz, ama hiç değilse çizgilerin daha kalın olması, harflerin koyu yazılması umarım zorluk çıkarmaz. Tikz’de bir “style” tanımı ile bunlar yapılabilir.
Bu marjlara açıklayıcı notlar da konabilir. Mesela 213. sayfada “Şimdi $GB$ paralelkenarı $C$, $KM$’ye eşit olduğundan, $GB$ paralelkenarı $KM$’den büyüktür” cümlesini okuyunca sanki bir hata varmış izleniminde kalıyoruz. Oysa hata yok. Tercümede kusur da yok. Belki burada sayfa kenarına “$GB$ paralelkenarının alanı $C$’nin alanı ile $KM$’nin alanının toplamına eşit olduğundan” gibi bir açıklama düşülebilir.
Bir de Bilim ve Teknik dergisindeki makalelere bir yenisi daha eklense, Öklid’in “ölçer”, “sürekli orantılı” gibi alışık olmadığımız terimlerini günümüzün terimlerine çeviren bir sözlük-makale yazılsa Öklid’in Elemanları‘nı okumak ve anlamak daha kolaylaşır.
Sonuç
Sertöz’ün ortaya çıkarttığı eser önünde saygıyla eğiliyorum. Tarihi önemi olan ve hâlâ tazeliğini koruyan Elemanlar‘ı Türkçeye kazandırmakla Sertöz Türkiye’nin matematiğine, matematik tarihine, bilimine, felsefesine, kültürüne çok büyük hizmette bulunmuştur. Bu çalışmasıyla matematik kitaplarının çevirisine de yeni bir standart getiriyor. Umulur ki piyasada dolaşan kalın ve pahalı ders kitaplarının çevirilerini “Google translate” düzeyinde yapanlar, Sertöz’ün tercümesine bakıp kendilerine çeki düzen verirler.
Sertöz, işini düzgün ve titizlikle yapan, azmini bozmayan, ustalara vefayı unutmayan kişilerin var olduğunu göstermekle de tarif edilmez bir hizmet yapmıştır. Kendisinden alıntı yaparak bu yazımızı sona erdirelim [ÖE, viii]:
“Tamani Usta’dan 200 yıl sonra ona yarım bıraktırılan işi tamamlama isteğinin bu topraklarda yeniden canlandığını görmek sevindirici.”
Kaynaklar
[Cantor]: Moritz Cantor, Vorlesungen über Geschichte der Mathematik (ikinci baskı), Teubner, Leipzig, 1894.
[Dedekind]: Richard Dedekind Gesammelte Werke III (Yayınlayanlar: Robert Fricke, Emmy Noether, Öystein Ore), Vieweg & Sohn, Braunschweig, 1932.
[Fermat]: Pierre de Fermat, Oeuvres de Pierre de Fermat I (Paul Tannery’nin çevirileriyle; sunan ve açıklayanlar: R.Rashed, Ch.Houzel, G.Christol), Albert Blanchard, Paris, 1999.
[Heath]: Sir Thomas L.Heath, Euclid’s Elements (ikinci baskı), Dover Publications, Inc., New York, N. Y., 1956.
[Kirsti]: Kirsti Andersen, Cavalieri’s method of indivisibles, Archive for History of Exact Sciences, 31, No. 4, 1985, 291-367.
[MSD]: Aimeric Malter, Dierk Schleicher, Don Zagier, New Looks at Old Number Theory, The American Mathematical Monthly, 120, No. 3, 2013, 243-264.
[ÖE]: Ali Sinan Sertöz, Öklid’in Elemanları, Tübitak, Ankara, 2019.
[Sertöz 1]: Ali Sinan Sertöz, Öklid ve Elemanlar’ı, Bilim ve Teknik, No. 602, Ocak 2018, 14-23. https://services.tubitak.gov. tr/edergi/yazi.pdf?dergiKodu= 4\&cilt=51\&sayi=602\&sayfa=14\& yil=2018\&ay=1\&yaziid=41350
[Sertöz 3]: Ali Sinan Sertöz, Öklid’i Okurken, Bilim ve Teknik, No. 604, Mart 2018, 74-83. https://services.tubitak.gov. tr/edergi/yazi.pdf?dergiKodu= 4\&cilt=51\&sayi=604\&sayfa=74\& yil=2018\&ay=3\&yaziid=41569
[Sertöz 4]: Ali Sinan Sertöz, Öklid ve Türkçesi, Bilim ve Teknik, No. 605, Nisan 2018, 74-83. https://services.tubitak.gov. tr/edergi/yazi.pdf?dergiKodu= 4\&cilt=51\&sayi=605\&sayfa=74\& yil=2018\&ay=4\&yaziid=41671
Öklid’in Elemanları hakkında bir yazı yazmamı öneren İlhan İkeda ve Olcay Coşkun’a teşekkür ederim.
$^1$: Heath burada “if $\dots$ be”, “there be $\dots$” yazmış, bu yapılar modern İngilizcede kullanımdan düşmüştür. Taklit edilmesin.
$^2$: Tanımı için Öklid’in Elemanları‘nda 333. sayfaya bakınız.
$^3$: İşaret ve sembolleri!

