Yazar: Serkan Özel (ozels@boun.edu.tr)
Yıl: 2022-4
Sayı: 114
Matematik bağlamında örüntü farklı araştırmacılar tarafından tanımlanmıştır. Örüntüyü, Rittle-Johnson, Fyfe, McLean ve McEldoon [1] tahmin edilebilir bir sıralama; Papic, Mulligan ve Mitchelmore [2] tekrarlanan düzenlilik ve Montague-Smith, Cotton, Hansen ve Price [3] belirli bir kuralı takip eden sayı ve şekillerin sistematik düzenlemesi olarak tanımlamıştır. Bazı matematikçiler matematiği örüntülerin bilimi, matematikçileriyse örüntülerin arayıcıları [4, 5, 6] olarak tanımlamıştır. Örüntüler matematik eğitimcileri tarafından matematiksel sorgulamanın yapı taşlarından kabul edilmiştir [7, 8]. Örüntü tanımları ele alındığında bir düzenin keşfedilmesi, içerisinde tekrar eden yapıların varlığının incelenmesi, sistematik bir yapının kurulması örüntülerin neden matematiksel sorgulama için bu denli önemli olduğuna anlatmaktadır.
Doğumdan sekiz yaşa kadar tanımlanan erken çocukluk dönemi, çocuğun sosyal, fiziksel, duygusal ve entelektüel gelişimi açısından oldukça önemlidir. UNESCO [9], erken çocukluk dönemindeki eğitimin ilkokula hazırlığın çok daha ötesinde önemine vurguda bulunmaktadır. Erken çocukluk dönemi beynin en hızlı gelişim gerçekleştirdiği dönemdir. Çalışmalar, beş yaşına kadar çocuklar için sağlanacak kaliteli bir eğitimin, onlara orta ve uzun vadeli önemli faydalar sağladığını göstermektedir [10]. Kaliteli erken çocukluk eğitimi almış çocukların, sınıf tekrarı ve özel eğitime ihtiyaç olma ihtimalinin daha düşük, ileri sınıflara daha hazırlıklı, liseden mezun olma ihtimalinin daha yüksek olduğu ve iş hayatında daha yüksek gelir elde ettikleri görülmektedir. Etkili bir eğitime erişim, çocukların önündeki yapısal engelleri kaldırmada önemli bir rol üstlendiği için erken çocukluk eğitimine vurgu daha da önem kazanmaktadır.
Matematik eğitimi araştırmacıları çocukların erken yaşlardan itibaren örüntü etkinlikleriyle tanışması ve çalışmasını desteklemektedir [11]. Dolayısıyla örüntüler birçok okul öncesi öğretim programının temel parçası haline gelmiştir [12]. Ülkemizde de okul öncesinden sekizinci sınıfa kadar olan matematik öğretim programında örüntülerin önemli bir rolü vardır [13]. Okul öncesi öğretim programları incelendiğinde örüntülerin, erken çocukluk matematiğinde oynadığı rol ortaya çıkmaktadır. Milli Eğitim Bakanlığı Okul Öncesi Eğitim Programı [13], 36-72 aylık çocukların bilişsel gelişimini 3 temel yaş kategorisinde ele alır: $(a)$ 36-48 ay, $(b)$ 48-60 ay ve $(c)$ 60-72 ay. Örüntüler her üç dönemde de bilişsel gelişim göstermesi gereken özellik olarak sunulmuştur. Ülkemizde okul öncesi kazanımları arasında çocukların bir örüntüyü kopyalayabilmesi, örüntünün kuralını belirtmesi, örüntünün eksik olan parçasını bulabilmesi ve özgün örüntüler oluşturabilmesi yer almaktadır [13]. Sarama ve Clements [14] tarafından erken çocukluk dönemi için hazırlanan araştırma temelli öğretim programı Building Blocks’ta örüntü ve geometrinin matematik öğrenimi için temel olduğu belirtilmektedir. Benzer şekilde, Smith [43] örüntüyü erken matematik eğitiminin temel konularından biri olarak sunar. Her ne kadar çalışmalar örüntünün önemine vurguda bulunsa ve öğretim programlarına dahil edilse uygulamada nasıl yer aldığını incelemek gerekmektedir.

Erken çocukluk dönemi eğitim ortamlarında da örüntüler yaygın olarak görülmektedir. Küçük çocuklar ve onların anne ve babaları, öğretmenleri, dinledikleri kitaplar, oynadıkları oyunlar ve izledikleri eğitici TV programları hep örüntülere vurgu yapmaktadır. Amerika Birleşik Devletleri’ndeki okul öncesi eğitim kurumlarında yapılan gözlemlerde 4 ve 5 yaşlarındaki çocukların oyunlarındaki en yaygın matematiksel etkinliğin örüntüleri ve şekilleri keşfetmek olduğu görülmüştür. Çocuklar gözlem süresinin % 20 ila % 40 arasında değişen bir kısmında örüntü ve şekilleri incelemişlerdir [15]. Araştırmalar okul öncesi öğretmenlerinin de örüntü etkinliklerine önem verdiğini göstermektedir [12, 16]. Tekrarlayan örüntüler yaygın olarak kullanılırken, genişleyen örüntüler nadiren kullanılmaktadır. Görsel 2’de tekrarlayan ve genişleyen örüntü türlerine örnekler sunulmuştur.
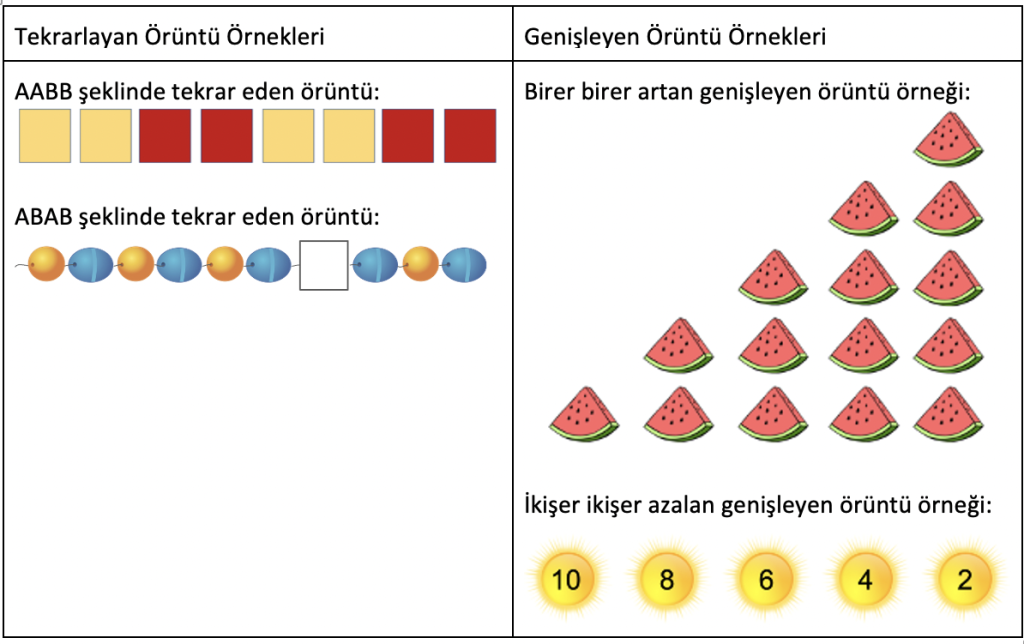
Örüntüler sadece erken çocukluk döneminde önemli bir konu değildir. Genel olarak matematik öğretiminde merkezi bir kavram olarak yer almaktadır [6, 14, 17]. Amerikan Ulusal Matematik Öğretmenleri Konseyi’nin [8] Okul Matematiği için Prensipler, Standartlar ve Beklentiler kitabında örüntüleri, ilişkileri ve fonksiyonları anlamayı cebir kazanımlarından biri olarak belirtmektedir. Bununla birlikte, matematik eğitimcileri örüntüleri cebirin temel konusu olarak ele almaktadır [2, 18, 19, 20]. Clements ve Sarama da [21] “Cebir, örüntüleri aramakla başlar. Örüntüleri belirlemek görünürde karmaşık olan durumlara düzen, bütünlük ve tahmin edilebilirlik getirir ve ilişkileri fark edip genellemeler yapmaya olanak sağlar” (s. 507) görüşünü dile getirmiştir.
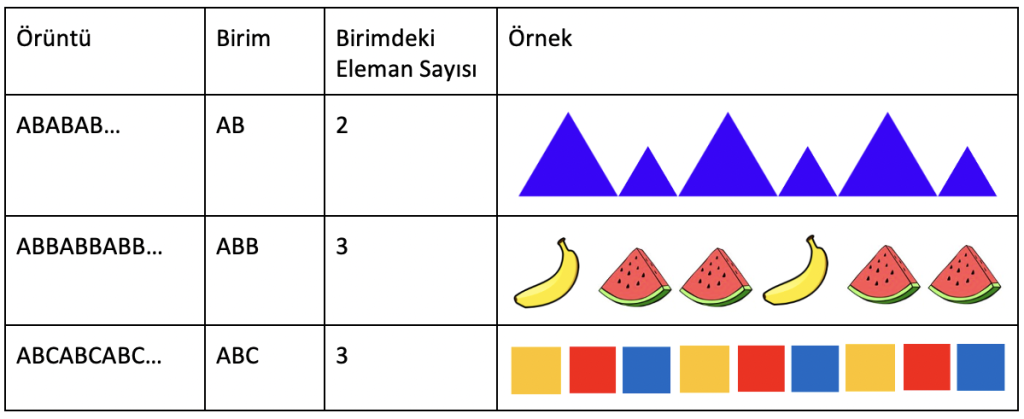
Örüntülerle ilgili yapılan yeni araştırmalar, örüntü bilgisinin matematik başarısının merkezinde yer aldığına dair güçlü kanıtlar sağlamaktadır [22]. Erken çocukluk döneminde çocukların karşılaştığı ilk örüntü türlerinden biri tekrarlayan örüntülerdir [23, 24]. Tekrarlayan örüntüler, döngüsel tekrarı olan ve tanımlanabilir bir “tekrar eden birimi” olan örüntülerdir [25]. Örneğin, ABBABBABB… örüntüsü, üçlü bir tekrar birimine sahiptir. Birim genellikle renk (örn. kırmızı-mavi-kırmızı-mavi-kırmızı-mavi…), şekil (örn. kare-daire-kare-daire-kare-daire…) veya büyüklük (örn. büyük-küçük-büyük-küçük-büyük-küçük,…) gibi temel boyutlarda değişiklik gösteren iki veya üç eleman (örn. AB, ABB, ABC) içerir (Tablo 1’e bakınız).
Araştırmalar tekrar eden örüntü bilgisi ile matematik başarısı arasında ilişkisel ve nedensel kanıtlar sağlamıştır [22, 26]. Boylamsal bir çalışma, okul öncesi, anaokulu ve birinci sınıfın sonunda sahip olunan örüntü becerisinin, diğer matematik, okuma, bilişsel ve demografik değişkenleri kontrol ettikten sonra bile, beşinci sınıfta matematik başarısını oldukça iyi tahmin ettiğini göstermiştir [27]. Altı aylık bir kontrollü deney çalışmasında, öğrenme zorluğu olan birinci sınıf öğrencileri tekrarlayan örüntü, sayısal beceriler, okuma veya sosyal bilgiler hakkında öğrenim gördükleri dört gruba rasgele atanmışlardır. Tekrarlayan örüntü eğitimi alan çocuklar, çeşitli standartlaştırılmış matematik değerlendirmelerinde, sayısal beceri eğitimi almış çocuklara benzer ya da daha iyi bir performans sergilemişler; okuma ya da sosyal bilgiler eğitimi alan çocuklardan sistematik olarak daha iyi başarı elde etmişlerdir [28, 29].
Eğitimciler, tekrarlayan örüntüleri keşfeden çocukların kavramların nedenlerine daha fazla değer verebileceğini belirtmiştir [30]. Tekrarlayan örüntülerdeki tekrar eden birime odaklanan özelleştirilmiş bir okul öncesi örüntü etkinliği, anaokulu çocuklarının hem tekrarlayan hem de genişleyen örüntüler hakkında daha fazla bilgi edinmelerine destek olmuştur [2]. Warren ve Cooper [20] öğrencilere tekrarlayan örüntüler hakkında eğitim verdikleri çalışmalarında örüntülerin orantıyı anlamada etkili bir köprü olduğunu görmüşlerdir. Ayrıca, ilkokuldaki örüntü bilgisi bir yıl sonraki cebirsel yeterliliği yordamaktadır [31]. Ortaya çıkan araştırma sonuçları çocukların örüntü anlayışının matematik performanslarında önemli bir rol oynayabileceğini göstermektedir. Belli başlı becerileri desteklemenin ötesinde, örüntü keşfi çocuklara genellemeleri gözlemleme ve sözlü olarak ifade edebilme ve onları sembolik olarak yazabilme olanağı sağladığı için, çocukların entelektüel gelişiminin önemli bir bileşenidir [32].
Erken Çocukluk Döneminde Örüntü Etkinlikleri
Çocuklar çevrelerindeki materyallerle doğal bir şekilde örüntüler oluştururlar. Örneğin, Waters [33] küçük bir kız çocuğunun oyuncaklarından kolye yapıp kolyeyi “kare, komik şekil, kare, komik şekil” olarak tarif ettiğini gözlemlemiştir. Okul öncesi kurumlarındaysa çocukların en sık karşılaştığı örüntü etkinlikleri örüntü oluşturma, var olan örüntüyü kopyalama ve tekrarlayan örüntüleri genişletme etkinlikleridir [12]. Örneğin, çocuklara ABBABB… örüntüsü gösterilip bunun aynısını yapmaları istenir (örüntüyü kopyalama) ya da örüntüyü devam ettirmesi (örüntüyü genişletme) beklenir. Çoğu 4-yaş çocuğun tekrarlayan örüntüleri kopyalayabildiği ya da genişletebildiği görülmüştür [30, 34]. Fakat örüntüleri kopyalama ya da genişletme matematiksel düşünmeye başvurmadan nesne eşleştirme stratejileri kullanarak da yapılabilir [35]. Görsel 3’te verilen örnek soruda çocuktan Fil, Elma, Ağaç, Ağaç örüntüsünü (ABCC) keşfedip, cevap şıklarından uygun olanı seçmesi beklenmektedir.

Ancak, nesne eşleştirme stratejisi kullanan çocuklar örüntünün yapısını keşfetmeden, fil, elma ve ağaç ile eşleşen şekilleri bulup (sırasıyla yıldız, kare, daire) doğru cevabı söyleyebilmektedir. Papic, Mulligan ve Mitchelmore [2] çocukların bu etkinlikleri tekrar eden birimi fark etmeden de yaptıklarını göstermiştir. Matematiksel örüntüler nesne eşleştirmenin ötesinde ilişkileri genelleme ve soyutlamaya dayanmaktadır. “Genelleme yapmak ve tahmin edebilmek için çocukların örüntüye ‘bundan sonra ne gelecek?’ diye bakmanın ötesine geçip örüntünün yapısını incelemeleri gerekmektedir. Bu da örüntünün tekrarlayan birimlerden meydana geldiğini görmeleri demektir” [12]. Dolayısıyla çocukların örüntü birimini (yani, örüntünün tekrar eden kısmını) belirlemeyi öğrenmeleri gerekmektedir [2].
Örüntüyü soyutlama becerisi, çocukların örüntü birimine odaklanmasına imkan tanır. Böylece örüntüyü kopyalama ve genişletme etkinliklerinden daha fazla matematiğe odaklanır [36]. Örüntüyü soyutlama aynı tür örüntüyü farklı nesneler kullanarak yapmayı gerektirir. Örneğin, çocuklara beyaz-yeşil-yeşil-beyaz-yeşil-yeşil örüntüsünü gösterip onlardan bu tür bir örüntüyü mavi ve kırmızı daireler kullanarak oluşturmaları istendiğinde çocukların örüntüyü soyutlamaları gerekecektir. Soyutlama örüntünün yüzeysel özelliklerinden ziyade genel yapısına odaklanmalarını gerektirir. Örüntüyü soyutlama nesne eşleştirme stratejisi kullanarak gerçekleştirilemez ve nesnelerin ötesinde ilişkilerin soyutlanmasını gerektirir [20, 36, 37].
Çocuklar örüntüyü soyutlamanın ötesinde örüntünün birimini, yani tekrar eden eleman kümesini, açık bir biçimde fark etmeyi de öğrenirler. Farklı çalışmalarda çocuklardan örüntünün tekrar eden kısmını söylemeleri veya işaretlemeleri [2, 20] ya da en az nesneyi kullanarak gösterilen örüntünün aynısını oluşturmaları istenmiştir. Yakın zamanda yapılan bir çalışmada 4 yaşındaki çocukların çoğunun örüntüleri kopyalayabildikleri, yarısına yakınının örüntüleri genişletebildiği ve çok az bir kısmının örüntüleri soyutlayabildiği görülmüştür [1]. Örüntüleri soyutlamanın, örüntüleri kopyalama ve genişletmeden daha zor olmasına rağmen bazı okul öncesi çocukları için yapılabilir olduğu görülmüştür. Örüntü birimini fark eden 4 yaşındaki çocuk sayısı ise oldukça azdır.

Bu çalışmanın sonunda Rittle-Johnson ve diğerleri [27], Clements ve Sarama’nın [37] tekrarlayan örüntü bilgisi için oluşturdukları kavram haritasını genişleterek dört basamaklı bir kavram haritası oluşturmuşlardır. Örüntü kavram haritasının birinci basamağında çocuklar örüntüleri kopyalarlar, ikinci basamakta örüntüleri genişletirler, üçüncü basamakta örüntüyü farklı materyaller kullanarak oluşturacak kadar soyutlayabilirler ve dördüncü basamakta çocuklar örüntünün en küçük birimini açık seçik bir biçimde fark edebilirler. Kavram haritası ve örnek görevler Tablo 2’de sunulmuştur.
Çocukların örüntü becerilerinin ölçülmesi ve etkinliklerin örüntü seviyelerine göre tasarlanması oldukça önemlidir. Tablo 3’te örüntü becerilerinin ölçülmesi için her seviyeye uygun örüntü maddeleri sunulmaktadır. Öğretmenler ve araştırmacılar için kısa ve uygulaması kolay bir ölçek geliştirilmiştir [39]. Bu ölçek aynı zamanda çevrimiçi uygulanabilecek şekilde yeniden hazırlanmış ve geçerlik güvenirlik çalışmaları yapılmıştır [40, 41].


Bu önemli konunun öğretmenler ve ebeveynler tarafından sistematik bir şekilde ele alınması için çalışmalarımız devam etmektedir [40, 41, 42]. Bu çalışmamızda, 48-84 aylık çocukların örüntüleme becerileri ve yürütücü işlev becerileri arasındaki ilişkiyi araştırıyoruz. Mevcut çalışmanın ara sonuçlarına göre hazırlamış olduğumuz önerilerle örüntü becerilerinin erken yaşta nasıl ele alınabileceği konusunda bir kılavuz [42] hazırladık. Örüntü ve örüntüyle ilgili bazı terimler, çocukların kelime hazinesinde olmadığı için özellikle daha küçük yaşlarda iletişim kurarken bir engel olarak karşımıza çıkabilmektedir. Bu açıdan çocuk ile örüntü çalışmalarında dikkatlerini günlük hayattaki örüntülere çekerek kavramsal olarak öğrenmeleri ön plana alınmalıdır (Görsel 4). Benzer şekilde hareketlerle veya müzikle de örüntüleri keşfetmelerine imkân verilebilir. Hem farklı seviyelere hitap eden hem de kolaydan zora ilerleyen bir öğrenme patikası oluşturmak örüntü kavramının sağlam bir şekilde içselleştirilmesi için de önemlidir.

Kaynaklar
[1] Rittle-Johnson, B., Fyfe, E. R., McLean, L. E., & McEldoon, K. L. (2013). Emerging understanding of patterning in 4-year-olds. Journal of Cognition and Development, 14, 376–396. http://dx.doi.org/10.1080/15248372.2012.689897
[2] Papic, M. M., Mulligan, J. T., & Mitchelmore, M. C. (2011). Assessing the development of preschoolers’ mathematical patterning. Journal for Research in Mathematics Education, 42(3), 237-268.
[3] Montague-Smith, A., Cotton, T., Hansen, A., & Price, A. J. (2017). Mathematics in Early Years Education. Routledge.
[4] Devlin, K. (1994). Mathematics: The science of patterns. New York: Henry Holt.
[5] Sawyer, W. W. (1955). Prelude to mathematics. London: Penguin.
[6] Steen, L. A. (1988). The science of patterns. Science, 240, 611-616.
[7] Clemson, D., & Clemson, W. (2001). Mathematics in the early years. New York: Routledge.
[8] National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
[9] UNESCO (ty). Early childhood care and education [Erken çocuklukta bakım ve eğitim]. https://www.unesco.org/en/education/early-childhood adresinden alınmıştır.
[10] National Education Association (ty). Early childhood education [Erken çocukluk eğitim]. https://www.nea.org/advocating-for-change/action-center/our-issues/early-childhood-education adresinden alınmıştır.
[11] Sarama, J., & Clements, D. (2009). Early childhood mathematics education research: Learning trajectories for young children. London: Routledge.
[12] Economopoulos, K. (1998). What comes next? The mathematics of pattern in kindergarten. Teaching Children Mathematics, 5(4), 230–233.
[13] Milli Eğitim Bakanlığı Temel Eğitim Genel Müdürlüğü. (2013). Okul öncesi eğitim programı. https://tegm.meb.gov.tr/dosya/okuloncesi/ooproram.pdf adresinden erişildi.
[14] Sarama, J., & Clements, D. H. (2004). Building Blocks for early childhood mathematics. Early Childhood Research Quarterly, 19, 181–189. http://dx.doi.org/10.1016/j.ecresq.2004.01.014
[15] Ginsburg, H. Lin, C. Ness, D. & Seo, K. (2003). Young American and Chinese children’s everyday mathematical activity. Mathematical Thinking and Learning, 5(4), 235–258.
[16] Clarke, B., Clarke, D., & Cheeseman, J. (2006). The mathematical knowledge and understanding young children bring to school. Mathematics Education Research Journal, 18(1), 78–103.
[17] Charles, R. (2005). Big ideas and understandings as the foundation for elementary and middle school mathematics. Journal of Mathematics Educationa Leadership, 73, 9–24.
[18] Burton, G. M. (1982). Patterning: Powerful play. School Science and Mathematics, 82, 39–44. http://dx.doi.org/10.1111/j.1949-8594.1982.tb17161.x
[19] Lee, L., & Freiman, V. (2006). Developing algebraic thinking through pattern exploration. Mathematics Teaching in the Middle School, 11, 428–433.
[20] Warren, E., & Cooper, T. (2006). Using repeating patterns to explore functional thinking. Australian Primary Mathematics Classroom, 11, 9–14.
[21] Clements, D. H., & Sarama, J. (2007). Mathematics. In R. S. New & M. Cochran (Eds.), Early childhood education: An international encyclopedia (Vol. 2, pp. 502-509). Westport, CT: Praeger.
[22] Zippert, E. L., Douglas, A.-A., Tian, F., & Rittle-Johnson, B. (2021). Helping preschoolers learn math: The impact of emphasizing the patterns in objects and numbers. Journal of Educational Psychology, 113(7), 1370–1386. https://doi.org/10.1037/edu0000656
[23] National Association for the Education of Young Children. (2014). NAEYC early childhood program standards and accreditation criteria. Washington, DC: Authors.
[24] National Council of Teachers of Mathematics (2006). Curriculum focal points for prekindergarten through grade 8 mathematics. Reston, VA: Author.
[25] Zazkis, R., & Liljedahl, P. (2002). Generalization of patterns: The tension between algebraic thinking and algebraic notation. Educational Studies in Mathematics, 49(3), 379–402.
[26] Nguyen, T., Watts, T. W., Duncan, G. J., Clements, D. H., Sarama, J. S., Wolfe, C., & Spitler, M. E. (2016). Which preschool mathematics competencies are most predictive of fifth grade achievement? In Early Childhood Research Quarterly (Vol. 36, pp. 550–560). Elsevier BV. https://doi.org/10.1016/j.ecresq.2016.02.003
[27] Rittle-Johnson, B., Fyfe, E. R., Hofer, K., & Farran, D. (2017). Early math trajectories: Low-income children’s mathematics knowledge from age 4 to 11. Child Development, 88(5), 1727-1742. https://doi.org/10.1111/cdev.12662
[28] Kidd, J. K., Carlson, A. G., Gadzichowski, K. M., Boyer, C. E., Gallington, D. A., & Pasnak, R. (2013). Effects of patterning instruction on the academic achievement of 1st-grade children. Journal of Research in Childhood Education, 27(2), 224-238. 10.1080/02568543.2013.766664
[29] Kidd, J. K., Pasnak, R., Gadzichowski, K. M., Gallington, D. A., McKnight, P., Boyer, C. E., & Carlson, A. (2014). Instructing first-grade children on patterning improves reading and mathematics. Early Education and Development, 25(1), 134-151. 10.1080/10409289.2013.794448
[30] Starkey, P., Klein, A., & Wakeley, A. (2004). Enhancing young children’s mathematical knowledge through a pre-kindergarten mathematics intervention. Early Child Research Quarterly, 19(1), 99–120.
[31] Lee, K., Ng, S. F., Bull, R., Lee Pe, M., & Ho, R. H. M. (2011). Are patterns important? an investigation of the relationships between proficiencies in patterns, computation, executive functioning, and algebraic word problems. Journal of Educational Psychology, 103(2), 269-281. 10.1037/a0023068
[32] English, L. D., & Warren, E. A. (1998). Introducing the variable through pattern exploration. Mathematics Teacher, 91(2), 166–170.
[33] Waters, J. (2004). Mathematical patterning in early childhood settings. In I. Putt & M. McLean (Eds.), Mathematics education for the third millennium (pp. 565–572). Townsville: Mathematics Education Research Group of Australia.
[34] Clements, D. H., Sarama, J. H., & Liu, X. H. (2008). Development of a measure of early mathematics achievement using the rasch model: The research-based early maths assessment. Educational Psychology, 28, 457– 482. doi:10.1080/01443410701777272
[35] Threlfall, J. (1999). Repeating patterns in the early primary years. In A. Orton (Ed.), Pattern in the Teaching and Learning of Mathematics. London: Cassell.
[36] Rittle-Johnson, B., Fyfe, E. R., Loehr, A. M., & Miller, M. R. (2015). Beyond numeracy in preschool: Adding patterns to the equation. Early Childhood Research Quarterly, 31, 101–112. http://dx.doi.org/10.1016/j.ecresq.2015.01.005.
[37] Clements, D. H., & Sarama, J. (2009). Other content domains. Learning and Teaching Early Math: The Learning Trajectories Approach, 189–202.
[38] Rittle-Johnson, B., Douglas, A., Zippert, E., Özel, S. & Tang, J. (2020) Test of Early Patterning Ability. Available from B. Rittle-Johnson, Vanderbilt University, Nashville, TN 37203
[39] Kaufman, J., Douglas, A., Camille, M., Özel, S., & Rittle-Johnson, B. (2021, September). Measuring Preschoolers’ and Kindergarteners’ Understanding of Different Types of Patterns. Paper presented online at the annual meeting of Society for Research on Educational Effectiveness 2021 Conference: The Fierce Urgency of Knowledge: Education Evidence for Reimagining and Reckoning. https://sree.confex.com/sree/2021/meetingapp.cgi/Paper/2875
[40] Kaufman, J., Douglas, A., Camille, M., Özel, S., & Rittle-Johnson, B. (2022, April). Measuring Preschoolers’ and Kindergarteners’ Understanding of Different Types of Patterns. Paper presented online at the bi-ennial conference of Cognitive Development Society. https://cogdevsoc.org/wp-content/uploads/2022/04/CDS2022AbstractBook.pdf
[41] Özel, S., Alvan, G., Özgünlü, M., Pesen, M., Şanlı, B., & Şeker, V. (2022). Ebeveynler için pratik örüntü etkinlik örnekleri kılavuzu. http://col.boun.edu.tr/index.php/publications/9-pattern-activities adresinden alınmıştır.
[42] Smith, S. S. (2006). Early childhood mathematics. Boston: Pearson.

