Yazar: Ali Nesin (anesin@nesinvakfi.org)
Yıl: 2022-3
Sayı: 113
Soru. Bir dikdörtgen, şekildeki gibi sonlu sayıda küçük dikdörtgene parçalanıyor. Küçük dikdörtgenlerin her birinin her iki kenarından en az biri bir doğal sayıysa, büyük dikdörtgenin kenarlarından en az birinin de bir doğal sayı olduğunu kanıtlayın.
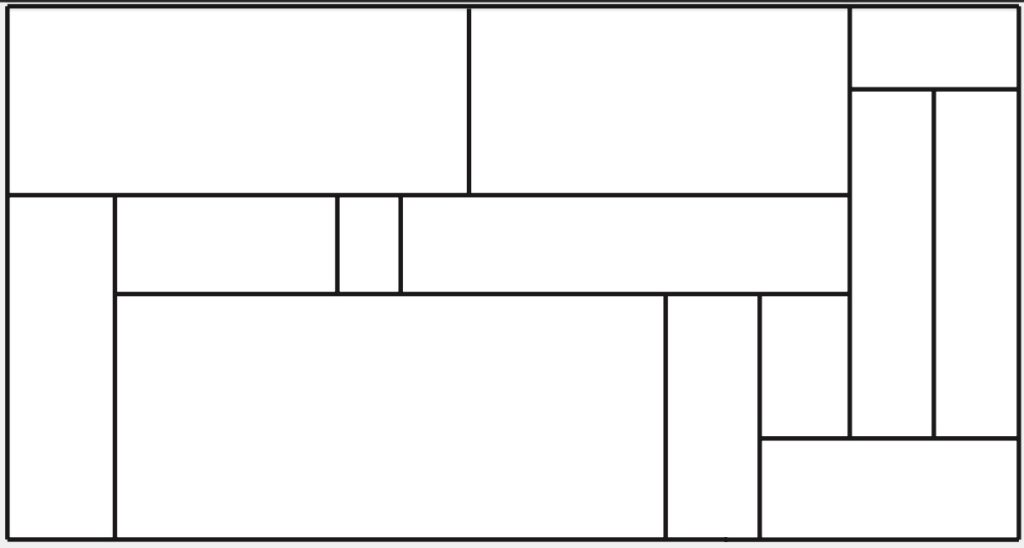
Sorunun Hikâyesi. Bu soruyu Matematik Köyü’nün gedikli hocalarından Fransız matematikçi Adrien Deloro sordu. Ecole Normale Supérieure’e yeni giren öğrencilere hocalardan biri sormuş. Amaç, matematikte her teoremin alışılmış genel yöntemlerle kanıtlanamayabileceğini göstermekmiş. Belki de aynı zamanda Ecole Normale Supérieure’e girmeyi başararak (aslında haklı ve kaçınılmaz olarak) şişen egolarını biraz söndürmek.
Kanıt: Herhangi bir dikdörtgeni, küçük karelerinin kenarları 1/2 olan bir satranç tahtasının üzerine (yatay ya da dikey olarak) yerleştirelim ve dikdörtgenimizin içindeki siyah ve beyaz alan miktarlarını karşılaştıralım.
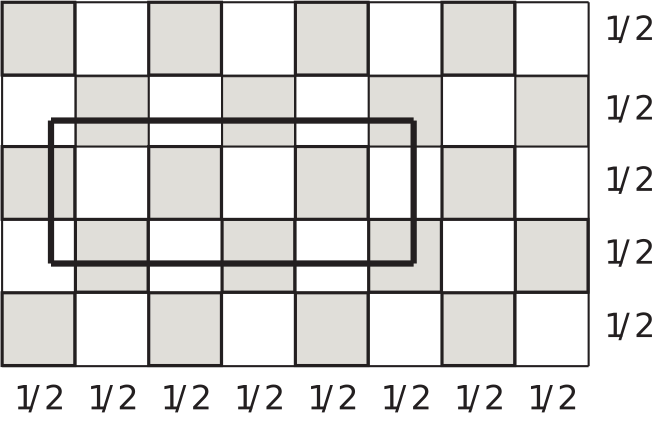
Tabii, siyah ve beyaz alan miktarları, dikdörtgenin satranç tahtasında yerleştirildiği konuma göre değişir. Ama eğer kenarlarından biri bir tamsayıysa, o zaman dikdörtgen (yatay ya da dikey olarak) nereye yerleştirilirse yerleştirilsin siyah ve beyaz alanlar hep eşit olur. Bunun, aşağıdaki şekillerden biraz açıklamayla, kolayca anlaşılacağını sanıyoruz.

En az bir kenarı bir tamsayı olan bir dikdörtgeni, yukarıdaki gibi, köşelerinden biri satranç tahtasının bir köşesinin üstüne gelecek biçimde yerleştirelim. (Örneğimizde yatay kenarın uzunluğu 3, bir tamsayı.) O zaman (satranç tahtasının kenarları 1/2 olduğundan) tamsayı uzunlukta olan kenar, çift sayıda satranç tahtası kenarı üzerine oturur (örneğimizde 6). Kolayca görüleceği üzere bu durumda dikdörtgenin içindeki siyah kareyle beyaz kare alanı eşittir.

Şimdi dikdörtgenimizi, yukarıdaki gibi, biraz yukarıya kaydıralım. Beyaz ve siyah alanlar alttan biraz kaybolur, ama bu kayıp üst taraftaki kazançla telafi edilir; sonuçta beyaz ve siyah alanlar değişmez.

Son olarak dikdörtgenimizi, yukarıdaki gibi, biraz sağa kaydıralım. Beyaz ve siyah alanlar soldan biraz kaybolur, ama bu kayıp sağ taraftaki kazançla telafi edilir; sonuçta beyaz ve siyah alanlar değişmez.
Demek ki en az bir kenarı tamsayı olan bir dikdörtgende beyaz ve siyah alanlar eşit olur.
Şimdi hiçbir kenarı tamsayı olmayan bir dikdörtgen alalım. Bu dikdörtgeni, aşağıdaki gibi, bir köşesi satranç tahtasının bir köşesinin üstüne gelecek biçimde yerleştirelim.
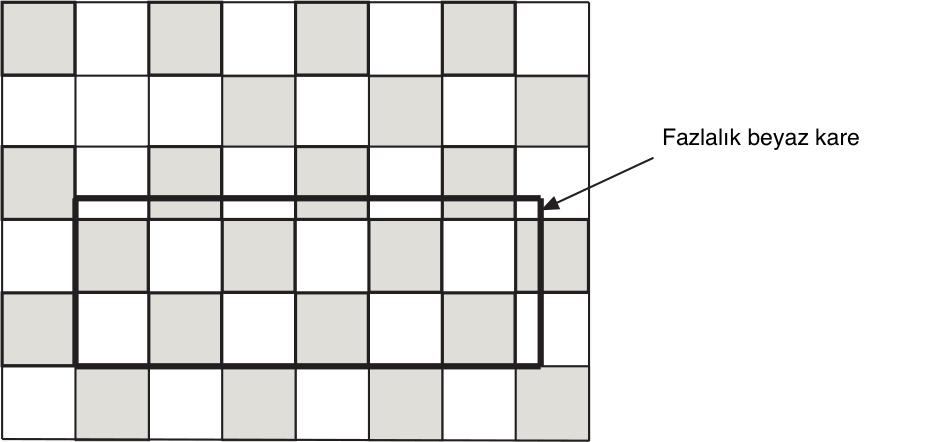
Küsuratlı kısım siyah ve beyaz kare arasındaki eşitliği kıracaktır (örnekte beyaz alan fazla çıkacaktır), yani bu pozisyonda dikdörtgenin beyaz ve siyah alanları eşit olmaz.
Demek ki bir dikdörtgenin en az bir kenarının uzunluğunun bir tamsayı olması için, dikdörtgenin, satranç tahtasına nasıl yerleştirilirse yerleştirilsin, içindeki siyah ve beyaz alanların eşit olması gerek ve yeter koşuldur.
Şimdi kanıtımıza gelelim. Bir dikdörtgen, en az bir kenarı tamsayı olan küçük dikdörtgenlerle kaplanmış olsun. Her bir küçük dikdörtgen satranç tahtasına nasıl yerleştirilirse yerleştirilsin, içindeki siyah ve beyaz alanlar eşittir. Demek ki aynı şey büyük dikdörtgen için de doğrudur, dolayısıyla büyük dikdörtgenin de en az bir kenarı bir tamsayıdır.

