Sayı Saymalı Kombinatorik

Yazar: Kağan Kurşungöz

Yıl: 2022-3

Sayı: 113

En genel anlamda kombinatorik sonlu yapılar üzerinde çalışır. Doğal sayılar, tamsayılar veya kesirler ilgi alanına girdiğindeyse, bir parametreye bağlı olarak bunları sınırlar ve yine sonlu alt kümelerle ilgilenir. Örneğin pay ve payda kısmı $N$’den büyük olmayan rasyonel sayılar böyledir.

Sayı saymalı kombinatorik, tanımında anlaşabildiğimiz bir yığının, topluluğun, listenin veya kümenin eleman sayısını belirlemekle ilgilenir. Elemanları birer birer parmakla göstererek, amiyane tabirle, armut gibi saymak olmaz. Bu metot bazı sınav sorularını çözmeye yarasa da teoride yeri yoktur.

Küme teorisinin etrafından dolaşabilmek için iyi tanımlı demedik de tanımında (karşılıklı) anlaşabildiğimiz dedik. Sonsuzluk kavramını hiç tartışmadık, çünkü sonsuzluk kombinatoriğin ilgi alanına girmez. Tecrübeli büyüklerimize ve akranlarımıza saygıda kusur etmeyelim, fakat matematiğin sayı saymayla başladığını okura hatırlatarak devam edelim. Bu yazıda çoğunlukla Brualdi [4] ve Stanley’den [9] esinleneceğiz.

Peki, birer birer saymayacaksak ne yapmamız bekleniyor? Örneklerle açıklamaya çalışalım. Bazı örneklerden yola çıkarak ilerideki yazılarda daha derin inceleyeceğimiz konular olacak. İyi bilinen örneklerin kanıtlarını biraz erteleyerek sunacağız.

Seçip sabitlediğimiz bir $n$ pozitif tamsayısı için $\{ 1, 2, \ldots, n \}$ kümesinin $2^n$ tane alt kümesi vardır. Sonlu bir kümenin alt küme sayısını eleman sayısına bağlı kapalı bir formülle ifade edebiliyoruz. Kapalı formülden kastımız girdinin büyüklüğünden bağımsız olarak, sabit sayıda işlemle
sonucu bulabildiğimiz formüldür. $2^n$’yi hesaplamak için $(n-1)$ tane çarpma yapmak gerekli diyenlere hak veriyoruz, fakat sayma problemlerinde sıkça karşımıza çıkan bazı ifadeleri de
kapalı formül kabul edeceğiz. Üs alma işlemi bunlardan birisi.

Biraz daha özelleştirilmiş bir örnek, yine $\{ 1, 2, \ldots, n \}$ kümesinin $k$ elemanlı alt kümelerinin sayısı olan binom katsayısı,
\[
\binom{n}{k} = \frac{n!}{ k! (n-k)! }.
\]
Burada $k$ sıfır veya pozitif bir tamsayı. $0!=1$ ve $n! = (n-1)! n$ olarak tanımladığımız faktöriyeli de kapalı formül sayacağız, çünkü o da sayı saymalı kombinatoriğin olmazsa olmazlarından.

Terim sayısı $n$’ye göre değişen genel toplamlar veya çarpımlar kapalı formül kabul edilmez. Örneğin,
\begin{align}
\nonumber
f(n) = a_1 + a_2 + \cdots + a_n = \sum_{j = 1}^n a_j
\end{align}
kapalı formül değildir, meğer ki toplamı,
\begin{align}
\nonumber
1 + 2 + \cdots + n = \frac{n(n+1)}{2}
\end{align}
örneğindeki gibi kapatabiliyor olalım.

İlk iki örneğimiz sayı saymalı kombinatorikte en istenen sonuçlardandır, çünkü sözkonusu objelerin sayısını kapalı bir formülle belirledik. Ne yazık ki böyle kapalı formüller bulmak, üzerinde çalıştığımız problemlerin tümü için mümkün değildir. Örneğin, bir pozitif tamsayının tamsayı parçalanışlarını saymak istediğimizi düşünelim. Bir tamsayı parçalanışının, terimleri büyükten küçüğe dizilmiş bir pozitif tamsayı toplamı olduğunu hatırlayalım. $$1 = 1, 2 = 2 = 1+1, 3 = 3 = 2+1 = 1+1+1$$ ve
\begin{align}
\nonumber
4 & = 4 \\ \nonumber
& = 3+1 \\ \nonumber
& = 2+2 \\ \nonumber
& = 2+1+1 \\ \nonumber
& = 1+1+1+1
\end{align}
olduğunu dikkate alarak 1’in bir, 2’nin iki, 3’ün üç, 4’ün ise 5 tamsayı parçalanışı olduğunu görürüz.

Bunları $p(1) = 1$, $p(2) = 2$, $p(3) = 3$ ve $p(4) = 5$ ile gösterirsek sorumuz $p(n)$’nin $n$’ye göre kapalı bir formülü olup olmadığına dönüşür. Böyle bir formül yakın zamana kadar bilinmemekteydi [3, 8], fakat yüz yıldan daha eski bir sonuç,
\begin{align}
\nonumber
p(n) \sim \frac{ \mathrm{e}^{ \pi \sqrt{\frac{2n}{3}} } }{ 4 n \sqrt{3} }
\end{align}
olduğunu söyler [6], yani
\begin{align}
\nonumber
\lim_{n \to \infty} \frac{p(n) 4 n \sqrt{3} }
{ \mathrm{e}^{ \pi \sqrt{\frac{2n}{3}} } } = 1.
\end{align}

Bu türden formüllere asimptotik formüller veya yaklaşık formüller denir. Kesin sonuçların bulunamadığı veya bunları bulmanın pratikte kullanılmayacak kadar uzun süreceği durumlarda yaklaşık formüller kullanılır. Bu formüller $p(n)$ gibi sayma fonksiyonlarının uzun vadede, yani $n$ sınırsız artarken, davranışını göz önüne serer.

Sayma problemlerinin çözümünde doğrudan sayma prensiplerini kullanabilir veya ampirik hesaplarla bir örüntü yakalayıp tümevarımla kanıtlayarak, dolaylı metotlardan da faydalanabiliriz. Dolaylı metotların en öne çıkanlarını örneklemeye çalışalım.

Ekleme-çıkarma prensibini veya bazı kaynaklarda geçtiği haliyle içerme-dışarma prensibini (İng. inclusion-exclusion) saymak istediğimiz yığından daha büyük bir yığının elemanlarından istenmeyenlerin ayıklanması olarak tarif edebiliriz. İstenen yığını doğrudan saymanın zor, fakat daha büyük yığının ve istenmeyenlerin sayılmasının daha kolay olduğu durumlarda ekleme-çıkarma prensibi tercih edilir. Saymak istediğimiz yığına istenmeyenleri ilave etmenin pratikte sınırsız sayıda yolu olduğundan ekleme-çıkarma prensibi doğrudan sayma metotlarına göre daha kuvvetli, buna karşılık yerine göre biraz hayal gücü isteyen bir metottur.

$A=\{ 1, 2, \ldots, n \}$ kümesinden $B=\{ 1, 2 \}$ kümesine bütün fonksiyonların sayısı $2^n$’dir. Bu fonksiyonlardan tam olarak iki tanesi sabit fonksiyonlar, yani birinin tüm görüntüleri 1, diğerinin tüm görüntüleri 2 olan fonksiyonlardır. Dolayısıyla $f:A \to B$ fonksiyonlarından örten olanların sayısı $2^n – 2$’dir. Tabii ki burada $B$ kümesinde 3 veya daha fazla eleman olsaydı işimiz çok daha zorlaşacaktı.
Bu problemin genel haldeki bir çözümünü başka bir yazıda göreceğiz.

Doğrudan sayma metotlarını kullanabilmemizden bağımsız olarak sayma problemlerine diğer bir yaklaşım üreteç fonksiyonlardır. Üreteç fonksiyonları vasıtasıyla kalkülüs veya analiz gibi matematiğin diğer dallarından da yardım alabildiğimiz için, sayma problemlerinin çözümünde bilinen en kuvvetli yöntem üreteç fonksiyonlardır. Sıfır veya pozitif tamsayı bir $n$ parametresine bağlı olarak cevabını $a_n$ olarak bulduğumuz bir sayma problemini düşünelim, mesela yukarıda bahsettiğimiz parçalanış sayıları $p(n)$. Sözkonusu $\{ a_n \}_{n \geq 0}$ dizisinin (adi) üreteç fonksiyonu,
\begin{align}
\nonumber
a_0 + a_1 x + a_2 x^2 + \cdots
= \sum_{n \geq 0} a_n x^n,
\end{align}
üstel üreteç fonksiyonuysa,
\begin{align}
\nonumber
a_0 + a_1 \frac{x}{1!} + a_2 \frac{x^2}{2!} + \cdots
= \sum_{n \geq 0} a_n \frac{x^n}{n!}
\end{align}
olarak tanımlanır. $a_n$ için kapalı bir formül bulamasak bile üreteç fonksiyonunun kapalı formülünü biliyorsak diziyi bildiğimizi kabul ederiz. Üreteç fonksiyonun analitik incelenmesi de bize sayma probleminin çözümü hakkında bilgi vermektedir. Üreteç fonksiyonları ayrı bir yazıda daha inceleyeceğiz, fakat burada da standart örneklerden birini verelim.

Diyelim ki elimizde yeterince 1 TL, 5 TL, 10 TL ve 20 TL var. $n$ TL’yi bunları kullanarak kaç farklı şekilde denkleştirebiliriz? Yeterinceden kastımız $n$ liranın tümünü istersek 1 TL’liklerden toplayabilmek. Örneğin $n = 6$ lirayı $6 \times 1$ TL veya $1 \times 5$ TL ve $1 \times 1$ TL olarak denkleştirebiliriz. Tamsayı parçalanışlarında olduğu gibi $1 + 5$ ve $5+1$ toplamlarını aynı kabul ediyoruz. Önce 1 TL vermişiz, sonra 5 TL vermişiz dert değil. Bu iki çözümün aslında,
\begin{align}
\nonumber
6 \cdot 1 + 0 \cdot 5 + 0 \cdot 10 + 0 \cdot 20 & = 6 \\ \nonumber
1 \cdot 1 + 1 \cdot 5 + 0 \cdot 10 + 0 \cdot 20 & = 6
\end{align}
toplamları olduğuna dikkat ettiğimizde çözümün $j_1$, $j_5$, $j_{10}$ ve $j_{20}$ sıfır veya pozitif tamsayılar olmak üzere,
\begin{align}
j_1 + 5 j_5 + 10 j_{10} + 20 j_{20} = 6 \quad\quad\quad (1)
\end{align}
denkleminin çözüm sayısı olduğuna dikkat edelim. [$(j_1, j_5, j_{10}, j_{20})= (6,0,0,0)$ veya $ =(1,1,0,0)$]. $(1)$ denklemini,
\begin{align}
\nonumber
x^{j_1 + 5 j_5 + 10 j_{10} + 20 j_{20}} = x^6
\end{align}
ve üstel ifadelerin özelliklerini kullanarak
\begin{align}
\nonumber
x^{j_1} (x^5)^{j_5} (x^{10})^{j_{10}} (x^{20})^{j_{20}} = x^6
\end{align}
olarak yazarsak, aslında sorunun çözümünün,
\begin{align}
& \left( 1 + x + x^2 + x^3 + \cdots \right)
\nonumber
\times \left( 1 + x^5 + x^{10} + x^{15} + \cdots \right) \\ \nonumber
& \times \left( 1 + x^{10} + x^{20} + x^{30} + \cdots \right) \\ \nonumber
& \times \left( 1 + x^{20} + x^{40} + x^{60} + \cdots \right) \quad \quad \quad (2)
\end{align}
çarpımının seri açılımında $x^6$’nın katsayısı olduğunu görmek zor değil. Seri açılımından kastımız polinomları çarpar gibi her parantezden bir terim seçip çarparak elde ettiğimiz bu çarpımları aynı üslerin katsayılarını birleştirerek toplamak. Aynı örnekten devamla, $x^6$ terimini elde etmek için ya birinci parantezden $x^6$ diğerlerinden 1 ya da ilk parantezden $x$, ikinci parantezden $x^5$, diğer ikisinden 1 seçeriz. Diğer seçimlerle $x^6$ elde etmemiz imkânsız. Böylece $(2)$ çarpımının seri açılımında $x^6$’nın katsayısı 2 olur. Yani 6 lirayı 1 TL, 5 TL, 10 TL ve 20 TL’likleri kullanarak iki farklı şekilde denkleştirebiliriz. $(2)$ çarpımındaki parantezleri yorumlamak zor değil. Örneğin ikinci parantezdeki 1 terimi hiç 5 TL’lik kullanmadığımızı, $x^5$ terimi yalnızca bir tane 5 TL’lik kullandığımızı, $x^{10}$ terimi tam olarak iki tane 5 TL’lik kullandığımız durumu $\ldots$ ifade ediyor.

Teorik detayları üreteç fonksiyonlardaki işlemleri incelediğimiz yazıya veya bir kalkülüs kitabına havale ederek,
\begin{align}
\nonumber
1 + x^5 + x^{10} + x^{15} + \cdots
= \frac{1}{1 – x^5}
\end{align}
gibi geometrik serileri kullanırsak, $(2)$ çarpımının aslında,
\begin{align}
\frac{1}{ (1 – x) (1 – x^5) (1 – x^{10}) (1 – x^{20}) } \quad\quad\quad (3)
\end{align}
kapalı formülüyle ifade edildiğini buluruz. Üreteç fonksiyonunu kapalı bir formülle ifade edebildiğimizden dolayı para denkleştirme problemini (veya para bozma problemini) çözdüğümüzü söyleriz. Çünkü $(3)$ rasyonel fonksiyonunun kuvvet serisinde $x^n$’nin katsayısı $a_n$, $n$ lirayı 1, 5, 10 ve 20 TL’liklerden istediğimiz kadarını kullanarak kaç farklı şekilde denkleştirebileceğimizi verir. Aslında $a_n$ için $n$’ye bağlı bir kapalı formül de bulmak mümkündür, fakat bunu inat edecek okura bırakalım. Bunu burada yapmamamızın bir sebebi işlemlerin çok uzun olması, ikinci ve daha önemli sebebiyse bahsettiğimiz kapalı formülü bulurken de $(3)$ üreteç fonksiyonundan faydalanıyor olmamızdır. Birçok sayma probleminde olduğu gibi burada da üreteç fonksiyonları çözümün bildiğimiz en doğal yöntemi.

Dolaylı sayma yollarından sıklıkla kullanılan biri de reküranslardır (fonksiyonel denklemler, özyinelemeler veya kendi kendini inşa eden diziler). Bu bağlamda ilk aklımıza gelen örnek Fibonacci sayıları olsa da biz farklı bir örnek vereceğiz. Diyelim ki ${ 0, 1, 2 }$ sembollerini kullanarak $n$ uzunluğunda kelimeler yazıyoruz. Barizdir ki $n$ uzunluğunda toplam $3^n$ tane kelime vardır. Fakat soruyu biraz değiştireceğiz ve bu $n$ uzunluğundaki kelimelerden kaç tanesinin ardışık iki tane 0 içermediğini soracağız. Bu sayıya $a_n$ diyelim. Ardışık iki sıfır içermeyen kelime 1 veya 2 ile bitiyorsa bu 1 veya 2’yi sildiğimizde elimizde kalan $(n-1)$ uzunluğundaki kelime de ardışık iki sıfır içermez. Öte yandan, ardışık iki sıfır içermeyen $(n-1)$ uzunluğundaki bir kelimenin sonuna 1 veya 2 yazarsak yine aynı şartı sağlayan $n$ uzunluğunda bir kelime elde ederiz. Yok, eğer bu kelime 0 ile bitiyorsa, son iki sembol 10 veya 20 olmak zorundadır, çünkü 00’a müsaade etmedik. Benzer bir eşlemeyi böylece $n$ uzunluğundaki 0 ile biten kelimeler ve $(n-2)$ uzunluğunda ardışık iki sıfır içermeyen kelimeler arasında yapabiliriz. Bu şekilde,
\begin{align}
a_n = 2 a_{n-1} + 2 a_{n-2} \quad\quad\quad (4)
\end{align}
buluruz. Ayrıca $a_0 = 1$ (boş kelime) ve $a_1 = 3$ (0, 1, 2 kelimelerinin üçü de istediğimiz şartı sağlamakta) olduğunu gözününe alırsak $a_n$ sayılarını iki başlangıç değeri ve bir rekürans ile
biricik belirlemiş oluruz. İlk birkaç değer:
\[
a_0 = 1, a_1 = 3, a_2 = 8, a_3 = 22, a_4 = 60, a_5 = 162, a_6 = 444, \ldots
\]

Aslında bu sayma problemine doyurucu bir çözüm bulmuş değiliz. Örneğin elimizde $a_n$ için kapalı bir formül yok. Fakat $(4)$ reküransının doğrusal (lineer) ve homojen olması, ayrıca katsayılarının da sabit olması bizi $a_n$’nin üreteç fonksiyonuna bakmaya sevkeder. Reküransın doğrusal olmasından kastımız paydada bir terim olmaması, terimlerin kareleri/küpleri vs alınmadan, sinüs/logaritma/üstel fonksiyon kullanılmadan, birbirleriyle çarpılmadan ($a_{n-1} a_{n-2}$ gibi) tek başlarına bulunması. Homojenden kastımız tüm terimlerin dizinin bir elemanını içermesi.
\begin{align}
\nonumber
A(x) = a_0 + a_1 x + a_2 x^2 + \cdots
= \sum_{n \geq 0} a_n x^n
\end{align}
diyelim.
\begin{align}
\nonumber
& x A(x) = \cdots = \sum_{n \geq 1} a_{n-1} x^n
\textrm{ ve } \
\nonumber
& x^2 A(x) = \cdots = \sum_{n \geq 2} a_{n-2} x^n
\end{align}
olacak. $n \geq 2$ için $(4)$ denklemini kullanırsak,
\begin{align}
\nonumber
& A(x) – 2x A(x) – 2x^2 A(x) &= a_0 + a_1 x – 2 a_0 x \\
\nonumber
& & = 1 + x,
\end{align}
çünkü $n \geq 2$ için $x^n$ terimlerinin tümünün katsayıları sıfır oldu. Son denklemin uçlarını $A(x)$ için çözersek de
\begin{align}
\nonumber
A(x) = \frac{1 + x}{ 1 – 2x – 2x^2}.
\end{align}
Artık üreteç fonksiyonunun kapalı formülünü elde ettiğimiz için $a_n$ dizisini tatmin edici bir biçimde belirlediğimizi söyleyebiliriz. Hatta kalkülüs ile biraz haşır neşir olmuş okur basit kesirlere ayrışımı kullanarak $a_n$ için kapalı bir formül de bulabilir. Görüldüğü üzere $a_n$ için bir kapalı formül elde etmek mümkün, fakat bunu elde etmek için reküranslar ve üreteç fonksiyonlar gibi dolaylı metotları kullanmak gerekti.

Son incelediğimiz örnekten hareketle doğrusal, homojen ve derecesi sabit reküranslarla belirlenen her dizinin rasyonel bir üreteç fonksiyonu olduğunu ve her rasyonel fonksiyonun bu tarzda bir diziyi belirlediği sonucunu çıkarabiliriz. Reküransın derecesi, gözüken en büyük ve en küçük indislerin farkıdır; örneğin $(4)$ reküransının derecesi 2’dir. Burada rasyonel fonksiyonun pay kısmının derecesinin paydanın derecesinden küçük olması gibi gözardı ettiğimiz detaylar olsa da anafikrin belli olduğunu düşünüyoruz. İlerideki yazılardan birinde üreteç fonksiyonlar üzerinde bazı işlemlerle daha sistematik eğileceğiz. Rasyonel üreteç fonksiyonlar üzerine daha derin bilgiler için okuru
Stanley [9] 4. bölüme yönlendiriyoruz.

Permütasyonlar ve Kombinasyonlar

Çok fazla sayma probleminin çözümünde karşımıza çıkmalarından dolayı permütasyonlar ve kombinasyonlar (özellikle binom katsayıları) kendi başlarına da ilgi çeken konular olagelmiştir. Aslında permütasyonun tanımı sonlu bir kümeden kendisine birebir ve örten fonksiyon olsa da sayma problemlerinde permütasyon elemanları seçip sıraya dizmeyi, kombinasyonsa sıradan bağımsız olarak seçim yapmayı ifade eder. En basit permütasyon ve kombinasyon formüllerini hesaplamadan önce saymanın temel prensiplerini hatırlayalım.

Toplama prensibi: $A$, $a$ elemanlı, $B$ de $b$ elemanlı ayrık kümeler olsun, yani $A \cap B = \varnothing$. $ \left\vert A \cup B \right\vert = a+b$, diğer bir deyişle $A \cup B$ birleşiminin eleman sayısı $a+b$’dir. Sayma problemlerine biraz daha yaklaşmaya çalışırsak, ya $A$’dan ya da $B$’den bir eleman seçmenin $a+b$ yolu vardır. Daha da somut bir örnek istersek Ankara’dan İstanbul’a üç farklı havayolu şirketinin uçuşlarıyla veya 10 farklı otobüs firmasının seferleriyle gidebiliyorsak, bu yolculuğu yapmanın $3+10 = 13$ farklı yolu vardır. Dikkat edelim ki kümelerin ayrık olması burada aynı anda hem uçağa hem otobüse binemememize denk geliyor.

Çarpma prensibi: $A$ $a$ elemanlı, $B$ de $b$ elemanlı kümeler olsun. O halde $\left\vert A \times B\right\vert = ab$, yani $A \times B$ kartezyen çarpımında $ab$ eleman vardır. Veya $A$ kümesinden bir tane, aynı anda $B$ kümesinden de bir tane eleman seçmenin $ab$ farklı yolu vardır. Buradaki önemli nokta seçimlerin ikisini de aynı anda yapmamız. Sayma problemlerinden çok beylik bir örnek verecek olursak beş gömlekten birini ve üç pantolondan birini seçerek giyinmenin $5 \cdot 3 = 15$ farklı yolu vardır.

Çıkarma prensibi: $A$, $a$ elemanlı, $B$ de $A$’nın $b$ elemanlı bir alt kümesi olsun. O halde $\left\vert A – B \right\vert = a-b$’dir veya $A$’nın $B$’den farkında $a-b$ tane eleman vardır. Yukarıda ekleme-çıkarma prensibine verdiğimiz örneği bu şablonda incelemek mümkündür.

Bölme prensibi: $A$, $a$ elemanlı bir küme olsun.Eğer $A$’yı her biri $k$ elemanlı $n$ tane ayrık alt kümenin birleşimi olarak yazabilirsek $n = \frac{a}{k}$ olur. Diğer bir deyişle, $A = A_1 \cup A_2 \cup \cdots \cup A_n$, öyle ki $\vert A_1 \vert$ $ = \vert A_2 \vert$ $= \cdots$ $= \vert A_n \vert$ $= k$ ve $1 \leq i < j \leq n$ için $A_i \cap A_j = \varnothing$ ise $n = \frac{a}{k}$ olur. Bu prensibin belki de en standart örneğini biraz ileride inceleyeceğiz.

$n$ elemanlı bir kümenin $k$ elemanlı permütasyonlarının sayısı $P(n, k)$ ile gösterilir ve $n$ elemanın içinden $k$ tanesini sırayı gözeterek kaç farklı biçimde seçebileceğimizin sayısıdır. Çarpma prensibi yardımıyla ilk elemanı $n$ farklı biçimde, ikinci elemanı $(n-1)$ farklı biçimde (çünkü birini zaten kullandık), $\ldots$, $k$. elemanı $(n-k+1)$ farklı biçimde seçebileceğimizden ve bu seçimleri aynı anda yapacağımız için
\begin{align}
\nonumber
& P(n, k) = n (n-1) (n-2) \cdots (n – k +1) \\ \nonumber
& = \frac{ n (n-1) \cdots 2 \cdot 1 }{ (n-k)(n-k-1) \cdots 2 \cdot 1 }
= \frac{n!}{(n-k)!}
\end{align}
hesaplarız. Aslında çarpma prensibini ifade ettiğimiz haliyle kullanmak istersek birkaç teorik detay daha serpiştirmemiz gerekir, fakat bunu yapmayacağız. Dileyen okur Brualdi’ye [4] bakabilir. $k = n$ seçtiğimizde $P(n,n) = n!$ hesaplarız, buna da kısaca $n$ tane elemanın permütasyon sayısı denir.

Bir önceki paragraftaki seçimleri sıra gözetmeksizin yaparsak elde edeceğimiz sayıya $n$ elemanın $k$’li kombinasyonu denir ve $\binom{n}{k}$ ile gösterilir. Diyelim ki $n$ elemandan $k$ tanesini sıra gözetmeksizin seçtik ki bunu yapmanın $\binom{n}{k}$ yolu vardır dedik. Bu $k$ elemanı şimdi $k!$ farklı biçimden biriyle sıralarsak bir permütasyon elde ederiz, hatta herhangi bir permütasyonu böyle elde edebiliriz. Demek ki $\binom{n}{k} k! = P(n, k)$, yani
\begin{align}
\nonumber
\binom{n}{k} = \frac{n!}{ k! (n-k)! }
\end{align}
Eğer $n$ elemanlı bir kümenin $k$ elemanlı permütasyonlarının kümesini, eleman sayıları aynı olan ayrık alt kümelere ayırabilirsek bölme prensibine bir örnek vermiş oluruz. Fakat bunu zaten yaptık sayılır. Aynı kombinasyondan türeyen $k!$ permütasyon istediğimiz bir alt kümeyi oluşturacak, bu ayrık alt kümelerin birleşimi de $n$ elemanlı bir kümenin $k$ elemanlı bütün permütasyonlarını verecek.
Belirtmeden geçmeyelim ki $\binom{n}{k}$ aynı zamanda, dikkatli okurun hatırlamış veya fark etmiş olacağı gibi, $n$ elemanlı bir kümenin $k$ elemanlı alt kümelerinin sayısını verir. Zira kümeyi oluştururken elemanların yazıldığı sırayı dikkate almayız.

Permütasyonlar

Bu alt bölümde $[n] = \{ 1, 2 \ldots, n\}$ kümesinin bütün permütasyonlarını ele alacağız. Permütasyonlar kendi başlarına ilginç olan kombinatorik nesnelerdir demiştik. Burada, permütasyonları istatistikler yardımıyla nasıl tasnif ettiğimize örnekler vereceğiz. Bir grup kombinatorik nesne üzerinde tanımlı bir istatistikten kastımız, her nesneyi bir tamsayıya götüren bir fonksiyondur. Permütasyonlar üzerinde tanımlı en bilinen iki istatistiği inceleyeceğiz: tersinme (İng: inversion) ve düşme (İng: descent) istatistikleri veya tersinme ve düşme sayıları.

$p(1) = p_1$, $p(2) = p_2, \ldots p(n)=p_n$ ile tanımlı $p = p_1 p_2 \cdots p_n$ permütasyonunu ele alalım. Bu gösterime tek satır gösterimi diyoruz. $i = 1, 2, \ldots (n-1)$ için $p_i > p_{i+1}$ eşitsizliğini sağlayan indislerin sayısına $p$’nin düşme sayısı denir. Örneğin $p = 25413$ permütasyonunun düşme sayısı 2’dir ($5>4$, $4>1$). Birim olmayan ($12 \cdots n$’den farklı olan) her permütasyonda en az bir düşme mevcuttur ve düşme sayısı $p$’nin birim permütasyondan ne kadar uzak olduğunu ölçer. Bu ölçeğe göre birim permütasyondan en uzak olan permütasyon $p = n(n-1) \cdots 21$’dir ve düşme sayısı olabilecek en yüksek değer olan $(n-1)$’dir. $\{ 1, 2, \ldots, n\}$’nin permütasyonlarından kaç tanesinin tam olarak $k$ düşme sayısına sahip olduğunu hesaplamayı orta zorlukta bir alıştırma olarak hevesli okura bırakıyoruz. Doğrudan sayma metotlarının çalışmadığını, dolaylı metotların kullanılması gerektiği ipucunu da verelim.

Birim permütasyondan ne kadar uzaklaştığımızın diğer bir ölçüsü de tersinme sayısıdır. Yine $p = p_1 p_2 \cdots p_n$ permütasyonunu düşündüğümüzde tersinme sayısı $i <j$ iken $p_i > p_j$ eşitsizliğini sağlayan indis ikililerinin sayısıdır. Diğer bir deyişle, permütasyonda bağıl sırası ters olan sayı çiftlerinin adedidir. Aynı örnekten devamla, $p = 25413$’ün tersinme sayısı 6’dır, çünkü ters sırada duran 6 tane çift vardır (2 ve 1, 5 ve 4, 5 ve 1, 5 ve 3, 4 ve 1, 4 ve 3). Yine bu ölçeğe göre birim permütasyondan en uzak olan permütasyon $p = n(n-1) \cdots 2 1$’dir, ve olabilecek en büyük tersinme sayısına sahiptir ( $\binom{n}{2}$ $=\frac{n(n-1)}{2}$, seçeceğimiz herhangi bir çift ters sırada duruyor). Yine, yalnızca birim permütasyonun tersinme sayısı sıfırdır. ${ 1, 2, \ldots, n }$’nin permütasyonları arasında tersinme sayısı $k$ olanları doğrudan sayamıyoruz, fakat bu sayıya $t(n, k)$ dersek bunların üreteç fonksiyonunun,
\begin{align}
\nonumber
& T_n(x) = \sum_{k = 0}^{\binom{n}{2}} t(n, k) x^k \
& = 1 (1 + x) \cdots
(1 + x + \cdots + x^{n-1}) \quad\quad\quad (5)
\end{align}
olduğunu tümevarımla gösterebiliriz. Aslında $(5)$ özdeşliğinin sağ tarafını kapalı formül kabul etmememiz gerekir, fakat cebirsel özdeşlikler yardımıyla,
\begin{align}
\nonumber
= \frac{(1 – x)(1 – x^2) \cdots (1 – x^n)}{(1-x)^n}
\end{align}
yazıp pay kısmındaki ifadeyi Pochhammer sem-bo-lü olarak tanıyıp $(x; x)_n$ notasyonuyla kısaltabiliriz [5]. Bu türden çarpımlar o kadar çok karşımıza çıkmaktadır ki artık aynı $n!$ gibi kapalı formül olarak kabul edilmektedir.

$n = 1$ için iddia aşikâr. $n \geq 2$ diyelim ve $(n-1)$ için iddianın doğruluğunu kabul edelim.
Diğer bir deyişle ${ 1, 2, \ldots, n-1 }$ kümesinin permütasyonlarını tersinme sayılarına göre tasnif ettiğimizde $T_{n-1}(x)$ üreteç fonksiyonunu elde ediyoruz. ${1, 2, \ldots, n}$ kümesinin bir permütasyonunu elde etmek için tek yapmamız gereken öncekilerden bir $p = p_1 p_2 \cdots p_{n-1}$ permütasyonu seçip $n$’yi yerleştirmek. Bunu yapabileceğimiz $n$ tane yol var: $n p_1 p_2 \cdots p_{n-1}$, $p_1 n p_2 \cdots p_{n-1}, \ldots, p_1 p_2 \cdots p_{n-1} n$. Bu permütasyonların her birinde $n$’yi saymazsak diğer sayıların oluşturduğu çiftlerden gelen tersinmeler korunuyor. İşin içine $n$’yi kattığımızdaysa $n p_1 p_2 \cdots p_{n-1}$’de yeni $(n-1)$ tane, $p_1 n p_2 \cdots p_{n-1}$’de yeni $(n-2)$ tane, $\ldots$ tersinme bulunuyor; $p_1 p_2 \cdots p_{n-1} n$’deyse yeni bir tersinme yok. Üreteç fonksiyonda $x$’in üssü tersinmeleri saydığından ve bu inşa herhangi bir permütasyondan başlayarak çalıştığından,
\begin{align}
\nonumber
T_n(x) = (x^{n-1} + x^{n-2} + \cdots + 1) T_{n-1}(x)
\end{align}
bularak tümevarım adımını, dolayısıyla kanıtımızı sonlandırıyoruz.

Permütasyon istatistiklerine yalnızca iki örnek vermekle yetineceğiz. Fakat belirtelim ki başka birçok permütasyon istatistiği vardır, hatta istatistiklerden daha genel şartları sağlayan permütasyonlar üzerinde de araştırmalar aktif olarak devam etmektedir. İlerideki yazılardan birinde permütasyonlarda örüntüden kaçınma konusundan bahsedeceğiz. Permütasyonlar hakkında daha geniş bilgi için okuru B’ona’ya [2] yönlendirelim.

Binom katsayıları

$n$ elemanlı bir kümenin $k$ elemanlı alt kümelerinin sayısını bir binom katsayısı olan $\binom{n}{k}$ olarak tespit etmiştik. Binom katsayıları çeşitli sayma problemlerinin çözümünde belki permütasyon sayılarından da fazla karşımıza çıkmaktadır. Binom katsayıları içeren özdeşliklerin bulunması ve kanıtlanması halen aktif bir araştırma alanıdır. Biz burada çözümü binom katsayısı olan çok genel bir problem ailesinden ve bir inşadan bahsedeceğiz, sonrasındaysa binom katsayısı özdeşliklerine örnekler vereceğiz.

Diyelim ki 13 özdeş şekeri 3 çocuğa paylaştıracağız. Bunu kaç farklı biçimde yapabiliriz? Problemi, hikâyesinden bağımsız olarak, $k_1 + k_2 + k_3 = 13$ denkleminin sıfır veya pozitif tamsayılarda kaç farklı çözümü olduğunun belirlenmesi olarak da sorabiliriz. Burada $k_j$, $j$. çocuğun aldığı şeker sayısı, $j= 1, 2, 3$. Birçok sayma problemini bu şablona oturtmak mümkündür. Şimdi bu denklemin belirli bir çözümünü, diyelim ki $2+3+8 = 13$’ü şöyle şematize edelim:
\begin{align}
\ast \ast \big\vert \ast \ast \ast \big\vert
\ast \ast \ast \ast \ast \ast \ast \ast .
\end{align}
13 yıldız ve 2 çubuk kullandık. İki çubuk yıldızları üç gruba ayırdı. Bu şekilde, $6+0+7 = 13$ çözümü de
\begin{align}
\nonumber
\ast \ast \ast \ast \ast \ast \big\vert \big\vert
\ast \ast \ast \ast \ast \ast \ast
\end{align}
olacak. Böylece, her bir çözümün 13 yıldız ve 2 çubuğun 15 boşluğa yerleşimine denk geldiğini, öte yandan 13 yıldız ve 2 çubuğun 15 boşluğa her yerleşiminin de $k_1 + k_2 + k_3 = 13$ denkleminin doğal sayılarda bir çözümüne denk geldiğini görmek kolay. Bu yerleşimi yapmanın $\binom{15}{2} = \binom{15}{13}$ yolu var.

Aynı soru çoklu kümelerin kombinasyon sayıları olarak da karşımıza çıkmaktadır. Çoklu küme elemanları yalnızca bir defa değil, istediğimiz kadar tekrarla yazabildiğimiz kümedir. Örneğin ${ a, a, b, b, b, c }$ $={ 2 \cdot a, 3 \cdot b, 1 \cdot c}$ bir çoklu kümedir. Elemanlardan bazılarını veya her birini sınırsız da tekrar edebilirdik. Örneğin $$M = { a, a, \ldots, b, b, \ldots, c, c, \ldots }$$ $$ = { \infty \cdot a, \infty \cdot b, \infty \cdot c }$$ üç çeşit elemanı olan ve her elemanın sınırsız defa tekrar ettiği bir çoklu kümedir. Bunu görmek için $M$’nin 13 elemanlı herhangi bir çoklu alt kümesinde yukarıda çözdüğümüz soru aynı zamanda bu $M$ kümesinin 13 elemanlı çoklu alt kümeleri sayısıdır. $a$’ların sayısının 1. çocuğun aldığı şeker sayısı, $\ldots$ olduğuna dikkat etmek yeterli. Bu bağlamda $M$’nin 13 elemanlı çoklu alt küme sayısına tekrarlı kombinasyon adı verilmektedir. Bazı kaynaklarda [9] bu $ \Big( \Big( \begin{array}{c} 13 \ 3 \end{array} \Big) \Big)$ ile gösterilmektedir. Bu noktada hevesli okuru yıldız ve çubukları kullanarak $ \Big( \Big( \begin{array}{c} m \ n \end{array} \Big) \Big) = \binom{m+n-1}{n}$ olduğunu kanıtlamaya davet ediyoruz.

Dikkatli okur neden tekrarlı kombinasyonlardan bahsedip tekrarlı permütasyonlardan bahsetmediğimizi soracaktır. Kendisini [4]’e yönlendireceğiz ve tekrarlı permütasyon problemlerinin aslında kombinasyon problemlerine dönüştürülebildiği ve cevaplarının binom katsayılarının çarpımıyla ifade edilebildiği notunu düşeceğiz.

Binom katsayısı özdeşliklerine vereceğimiz örnek yine iyi bilinen örneklerden olan Vandermonde özdeşliği:
\begin{align}
\nonumber
\sum_{j = 0}^r \binom{m}{j} \binom{n}{r-j} = \binom{m+n}{r}
\end{align}

Gözüken bütün parametreler sıfır veya pozitif tamsayıdır ve üst indisin alt indisten küçük olduğu binom katsayılarıysa sıfırdır. Bu özdeşliğin cebirsel, analitik, bilgisayar destekli, birçok kanıtı mevcuttur,
fakat biz onu sayarak kanıtlayacağız. Diyelim ki bir lisede 10. sınıflardan $m$ kişi, 11. sınıflardan $n$ kişi satranç kulübünde ve bu oyunculardan $r$ tanesi seçilerek bir turnuvaya gönderilecek.
Bu seçimi yapmanın $\binom{m+n}{r}$ yolu var. Öte yandan öğrencilerin sınıflarını dikkate aldığımızda 10. sınıflardan $j$ kişi seçersek 11 sınıflardan $(r-j)$ kişi seçmemiz gerekir. $j = 0, 1, 2, \ldots, r$ olabilir. Herhangi bir $j$ için bu seçimleri yaptığımızda $\binom{m}{j} \binom{n}{r-j}$ farklı takım oluşturabiliriz. Binom katsayılarını çarptık, çünkü bu seçimi aynı anda yapmamız gerekiyor. Son olarak, $j$ aynı anda iki farklı değer alamayacağından ve $0, 1, 2, \ldots r$ değerlerinden birini alması gerektiğinden bulduğumuz binom katsayısı çarpımlarını $j$’nin alabileceği değerler üzerinden toplar ve farklı takımları sol taraftaki toplamla saymış oluruz.

Dediğimiz gibi artık binom katsayısı özdeşliklerini göstermenin yolu Petkovsek, Wilf ve Zeilberger’in $A=B$’de detaylı anlattığı gibi [7] bilgisayar destekli tam otomatik kanıtlardır. Sayarak kanıtların değeri bize özdeşlikle ilgili daha derin bilgi vermeleri ve yeni özdeşlikler keşfetmek için ilham olmalarıdır.

Ekleme-Çıkarma Prensibi

Ekleme-çıkarma prensibi (kimi kaynaklarda içerme-dışarma prensibi) $n$ tane kümenin (diyelim $A_1$, $A_2$, $\ldots$, $A_n$) birleşimindeki eleman sayısını kümelerin ve kesişimlerinin eleman sayılarının bir bileşimi olarak hesaplamaya yarar. Örneğin iki kümemiz olsaydı,

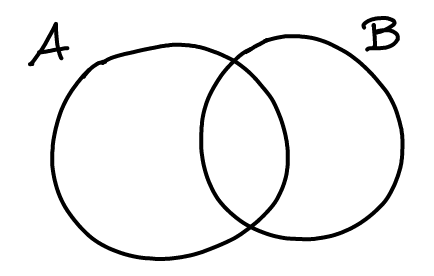
$\vert A \cup B \vert$ $= \vert A \vert$ $+ \vert B \vert$ $- \vert A \cap B \vert$ olacaktı. Bunun kanıtı basittir. Yalnızca $A$’ya ait elemanlar ($A-B$’nin elemanları) $\vert A \vert$ ile bir defa; yalnızca $B$’ye ait elemanlar ($B-A$’nın elemanları) $\vert B \vert$ ile bir defa; hem $A$’ya hem $B$’ye ait elemanlar $\vert A \vert$, $\vert B \vert$ ve $\vert A \cap B \vert$ ile birer defa, fakat $\vert A \cap B \vert$’nin önünde eksi işareti olduğundan $2 – 1 = $ 1 defa sayılmaktadır.

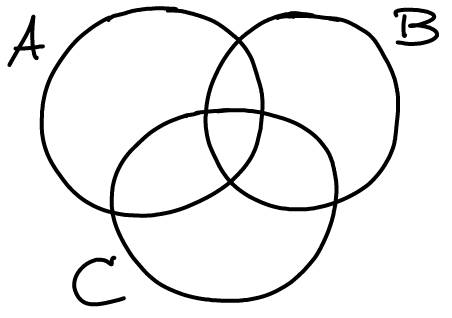
Üç kümemiz olursa bu sefer,
\begin{align}
\vert A \cup B \cup C \vert
= \vert A \vert + \vert B \vert + \vert C \vert – \vert A \cap B \vert – \vert A \cap C \vert – \vert B \cap C \vert \vert A \cap B \cap C \vert
\end{align}
yazacaktık. Bunun kanıtı da önceki paragraftakine benzer biçimde $A – (B \cup C)$, $(A \cap B) – C, \ldots$ gibi yedi farklı bölgedeki elemanların her birinin iddia ettiğimiz toplamda bir ve yalnız bir defa sayıldığını göstermektir.

Prensibin $n$ küme için olan halini yazmadan önce beylik örneklerden birini verelim. $1 \leq k \leq 1000$ aralığındaki tamsayılardan kaç tanesi 7, 11 veya 13 sayılarından en az biriyle bölünmektedir? Açıktır ki $A$ kümesini 7’nin, $B$ kümesini 11’in, $C$ kümesini de 13’ün katları olarak tanımlarsak, mesela $A \cap B$ kümesi 7 ve 11’in ortak katlarının en küçüğü olan 77’nin katları olacak. Fark edileceği üzere $A \cup B \cup C$ birleşiminin eleman sayısını hesaplamak kolay değil, ama tek tek kümelerin ve kesişimlerinin eleman sayılarını hesaplamak kolay. 1 ile 1000 arasında 7’ye bölünen $\lfloor \frac{1000}{7} \rfloor$ $=142$ sayı var. Kullandığımız tamdeğer fonksiyonu $\lfloor x \rfloor$ herhangi bir $x$ gerçel sayısı için $\lfloor x \rfloor \leq x < \lfloor x \rfloor + 1$ eşitsizliklerini sağlayan biricik tamsayı. $\frac{1000}{7}$ $=142,857142\ldots$ hesapladığımızda 7’nin 142 katının (994) 1000’den küçük olduğunu, fakat 143 katının (1001) 1000’den büyük olduğunu görüyoruz. Bu sebeple tamdeğer fonksiyonunu kullandık.
\begin{align}
\nonumber
& \left\lfloor \frac{ 1000 }{ 11 } \right\rfloor = 90,
\left\lfloor \frac{ 1000 }{ 13 } \right\rfloor = 76,
\left\lfloor \frac{ 1000 }{ 77 } \right\rfloor = 12, \
\nonumber
& \left\lfloor \frac{ 1000 }{ 91 } \right\rfloor = 10,
\left\lfloor \frac{ 1000 }{ 143 } \right\rfloor = 6,
\left\lfloor \frac{ 1000 }{ 1001 } \right\rfloor = 0
\end{align}
ve yukarıdaki üç kümenin birleşiminin eleman sayısı formülü yardımıyla sorumuzun cevabını $142+90+76-12-10-6+0 = 280$ buluruz. Burada 77, 91, 142 ve 1001 sırasıyla 7 ve 11’in, 7 ve 13’ün, 11 ve 13’ün ve 7, 11 ve 13’ün en küçük ortak katları. Aslında bu örnekte yalnızca çarpımları. Üçlü kesişimin boş küme çıkması gözümüzden kaçmaması gereken bir detay.

Küme sayısını $n$ parametresiyle belirlediğimizde,
\begin{align}
\nonumber
& \vert A_1 \cup A_2 \cup \cdots \cup A_n \vert \\
\nonumber
& = \vert A_1 \vert + \vert A_2 \vert + \cdots + \vert A_n \vert \\
\nonumber
& – \sum_{1 \leq i_1 < i_2 \leq n} \vert A_{i_1} \cap A_{i_2} \vert \\
\nonumber
& + \sum_{1 \leq i_1 < i_2 < i_3 \leq n} \vert A_{i_1} \cap A_{i_2} \cap A_{i_3} \vert \\
\nonumber
& \vdots \\
& + (-1)^{n-1} \vert A_1 \cap A_2 \cap \cdots \cap A_n \vert \quad\quad\quad (6)
\end{align}
olur. Sözlü olarak ifade etmeye çalışırsak, birleşimdeki eleman sayısını hesaplamak için önce bütün kümelerin ayrı ayrı eleman sayılarını topluyoruz, sonra bütün ikili kesişimlerdeki eleman sayılarını ayrı ayrı çıkarıyoruz, sonra bütün üçlü kesişimlerdeki eleman sayılarını ayrı ayrı topluyoruz $\ldots$

Kanıtın anafikrini bir örnekle açıklayalım. Aslında öğrencilere de sürekli hatırlattığımız üzere örnekle kanıt olmaz. Fakat yazıyı, dolayısıyla okuru, indislerde boğmak istemiyoruz. Diyelim ki $x \in$ $A_1 \cup A_2 \cup \cdots \cup A_n$, $x \in A_2$, $x \in A_4$, $x \in A_7$, $x \in A_{20}$ ve diğer kümeler için $x \not\in A_j$. Böylece $x$’in $(6)$da sayılacağı terimler $\vert A_{2} \vert$, $\vert A_{4} \vert$, $\vert A_{7} \vert$, $\vert A_{20} \vert$, bu dört kümenin ikili kesişimleri, yine bu dört kümenin üçlü kesişimleri ve nihayet bu dört kümenin dörtlü kesişimi. Kümelerin ayrı ayrı eleman sayıları $+$ ile, ikili kesişimleri $-$ ile, üçlü kesişimleri yine $+$ ile ve nihayet dörtlü kesişimleri $-$ ile sayılıyor. Tekli kümeler dört adet, ikili kesişimleri $\binom{4}{2} = 6$ adet, üçlü kesişimleri $\binom{4}{3} = 4$ adet ve nihayet dörtlü kesişimleri $\binom{4}{4} = 1$ adet. Sonuç olarak, ele aldığımız $x$ elemanı $(6)$ ifadesinde $4 – \binom{4}{2} + \binom{4}{3} – \binom{4}{4}$ $ = 4-6+4-1$ $= 1$ defa sayılıyor.

Kanıtın genel argümanı da $A_1$, $A_2$, $\ldots$, $A_n$ kümelerinden tam olarak $r$ tanesinde bulunup (diyelim ki $A_{i_1}$, $A_{i_2}$, $\ldots$, $A_{i_r}$) diğer $(n-r)$ kümede bulunmayan elemanlardan her birinin $(6)$ ifadesi ile kaç defa sayıldığı ($r = $ 1, 2, $\ldots$, $n$). Benzer bir mantıkla böyle her eleman,
\begin{align}
& \binom{r}{1} – \binom{r}{2}+\binom{r}{3} – \cdots +(-1)^{r-1} \binom{r}{r} \\
\nonumber
& 1 – \left( 1 – 1 \right)^r = 1
\end{align}
defa sayılıyor. Sondan bir önceki adımda kanıtlamadığımız binom teoremini kullandık. Atladığımız bu detay için okuru herhangi bir ayrık matematik (İng. discrete mathematics) ders kitabına veya internet arama motorlarına yönlendireceğiz.

Yukarıda $n = 2$ için yaptığımız kanıtta genel durumdaki iki kümenin birleşiminde üç bölgeden, $n = 3$ için işaret ettiğimiz kanıtta da yedi bölgeden bahsetmiştik. Bu bölgelerin sayısını her $n$ için bulalım. $x \in$ $A_1 \cup A_2 \cup \cdots A_n$ ise $x$ en az bir $A_j$’nin elemanıdır, fakat tümünün de elemanı olması gerekmez. $x \in A_1$ veya $x \not\in A_1$ olabilir, $x \in A_2$ veya $x \not\in A_2$ olabilir, $x \in A_n$ veya $x \not\in A_n$ olabilir dersek her küme için iki farklı durum olduğundan ve iki farklı küme için bu seçenekler bağımsız olduğundan toplam $2^n$ seçenek olur. Fakat $x \not\in A_1$, $x \not\in A_2$, \ldots, $x \not\in A_n$ durumunu elememiz gerekir, çünkü böyle bir eleman birleşimde yer alamaz. Dolayısıyla $n$ kümenin genel durumunda $n = 2$ ve $n = 3$ durumlarında çizildiğine benzer $2^n – 1$ bölgesi vardır. Bu bölgeleri kümelerin Venn şemalarını çizerek belirtmek ayrı bir uğraştır. Hatta Venn şemalarını belirli geometrik koşulları sağlarken çizmek bir araştırma konusudur!
Fakat sayı saymadan sapmamak adına bu bahsi burada kapatacağız.

Hevesli okura $n$ elemanlı bir kümeden $m$ elemanlı bir kümeye örten fonksiyonların sayısını ekleme-çıkarma prensibine benzer biçimde hesaplama problemini önerelim. Ekleme-çıkarma bahsini kapatmadan önce 1 ile 1000 arasındaki sayılardan, kaçının 7, 11 ve 13’ten en az birine bölündüğünü hesaplarken aslında bu sayılardan hiçbirinin bu asalların üçüne birden bölünmediğini, dolayısıyla 7’nin katları, 11’in katları ve 13’ün katlarından oluşan kümelerin bu sınırlar içinde kesişmediğini görmüştük. Kümelerin genel halde olmadığı, yani her kesişimin boş kümeden farklı olmadığı durumlarda
ekleme-çıkarma formülü $(6)$ çok daha sade bir hale gelebilir. Hatta bazı kesişimlerin eşit olduğu durumlarda katsayılar $+1$ veya $-1$’den farklı tamsayılar da olabilir. Bu konuya giriş yapmak için bile birkaç sayfa daha yazmamız gerektiğinden okuru Stanley’de kısmi sıralı kümelerden bahseden 3. bölümü [9] okumaya davet ediyoruz.

Sayma Problemlerine Genel Bir Bakış

Eğer yeteri kadar zorlarsak hemen hemen her sayma problemini kutulara top yerleştirme problemlerinden biri olarak modelleyebiliriz. Tabii ki bu yerleştirmeyi yaparken koymamız gerek kurallar
problemi doğallıktan çok uzaklaştırabilir. Bir bu bölümde bahsettiğimiz türden problemleri
kutuların işaretli veya özdeş olması ve topların işaretli veya özdeş olmasının ima ettiği dört durumda inceleyeceğiz.

Stanley [9] birinci bölümde de bu yaklaşım biraz daha soyut ve biraz daha özelleştirilmiş haliyle ele alınmıştır. Stanley, önce sonlu bir kümeden başka bir sonlu kümeye fonksiyonları düşünmüştür. Sonuçta kutulara top yerleştirmek de topların kümesinden kutuların kümesine bir fonksiyondur. Sonra, bu fonksiyonların kısıtsız hallerini ele aldığı gibi birebir veya örten olduğu durumları da ele almıştır.
Kutulara top yerleştirme modeline geri dönersek, bunlar sırasıyla her kutuda en fazla bir top olması veya her kutuda en az bir top olmasıdır. Kutuların işaretli veya işaretsiz, topların da işaretli veya işaretsiz olması fonksiyonları birer birer değil de uygun denklik bağıntılarının denklik sınıflarının sayılması problemine dönüştürmektedir. Okuru, Stanley [9] birinci bölümdeki “12’li yol” (İng. the twelvefold way) başlığını da okumaya davet ediyoruz.

Kutular da toplar da işaretli

Kutulara topları kaç farklı biçimde yer-leş-ti-re-bi-le-ce-ği-mi-zi saydığımız durumlardan en kolayı budur. Önce somut bir örnek üzerinde çalışalım, sonra bunu genelleyelim.

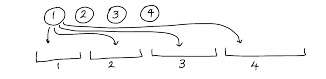
Diyelim ki 1, 2, 3, 4 numaralarını verdiğimiz dört top ve 1, 2, 3, 4 numaralarını verdiğimiz dört de kutu var. Her bir topu yerleştirebileceğimiz dört adet seçenek var. Bu seçeneklerin her biri farklı yerleşimlere tekabül eder, çünkü hem kutuları hem de topları birbirinden ayırabiliyoruz. Her bir top için yaptığımız seçim diğerlerinden bağımsız, dolayısıyla bu somut örnekte sorumuzun yanıtı $4^4$. Biraz geriden bakan okur perdenin arkasında aslında 4 elemanlı bir kümeden 4 elemanlı bir kümeye fonksiyonları saydığımızı fark etmiştir. Yani, genel halde, $n$ tane top, $m$ tane kutu varken sorunun cevabı $m^n$’dir.

Burada Stanley’nin ele aldığı durumlardan birini de hemen incelemek mümkün. Eğer her kutuda en fazla bir top olacaksa cevap,
\begin{align}
\nonumber
m (m-1) \cdots (m-n+1)
\end{align}
olur.
Nihayet birebir fonksiyonları sayıyoruz. Toplar kutulardan fazla olsa da sorun yok, neden?

Her kutuya en az bir top istersek, yani örten fonksiyonları saymaya çalışırsak, işimiz biraz daha zor. Okura bu problemi ekleme-çıkarma başlığında zaten sormuştuk. İlerideki yazılardan birinde bu problemin bir çözümünü de takdim edeceğiz.

Kutular işaretli, toplar özdeş

Bir önceki başlıktaki problemin bir permütasyon problemi olduğunu fark eden okur, bu durumda da problemin aslında bir kombinasyon problemi olduğunu fark edecektir. Yine önce somut bir örnek verelim. Dört özdeş top, dört de işaretli kutu olsun. Bu topların kutulara yerleşimlerinden biri şekilde gösterilmiştir.

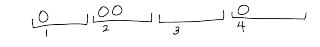
Bu dizilişte birinci kutudaki topla ikinci kutudaki toplardan birinin yerini değiştirirsek hiçbir şey fark etmiyor, çünkü toplar özdeş. Ama dördüncü kutudaki topu alıp üçüncü kutuya koyarsak farklı bir diziliş elde ediyoruz, çünkü kutuları birbirinden ayırabiliyoruz. Demek ki bütün dikkat etmemiz gereken, her bir kutudaki topların sayısı. Aslında bu, yukarıda binom katsayılarının uygulamalarını örneklerken bahsettiğimiz dört çocuğa dört özdeş şekeri dağıtma problemi. Haliyle cevabı da $\binom{4+3}{4}$. Şekilde gösterdiğimiz dağılımın, yıldız ve çubukları kullanarak,
\begin{align}
\nonumber
\ast \big\vert \ast \ast \big\vert \big\vert \ast
\end{align}
olduğuna dikkat edersek cevabı hemen yazabiliyoruz.

Genel halde, yani $m$ tane özdeş topu $n$ tane işaretli kutuya dağıtmanın tam olarak $\binom{m+n-1}{m}$ farklı yolu olduğu sonucunu çıkarırız. Bu başlıkta da her kutuda en az bir top olduğu durumun
veya her kutuda en fazla bir top olduğu durumun incelenmesi kolaydır. Bu durumlarda sorunun cevabını yazmayı da okura bırakıyoruz. İki halde de cevap birer binom katsayısı olacak.

Kutular özdeş, toplar işaretli

Bu durum yazıda şu noktaya kadar bahsetmediğimiz, bir eşdeğerinden de bahsetmediğimiz, bir sayma problemi. Önce somut bir örnek üzerinde sezgi geliştirmeye çalışalım. Dört adet işaretli topun dört özdeş kutuya bir yerleşimi şekilde gösterilmiştir.

Bu yerleşimde dört numaralı topu alıp öteki boş kutuya koysak hiçbir şey değişmeyecek, çünkü sonrasında o kutuyu içindeki topla birlikte boş olan kutuyla yer değiştirip şekilde gösterilen dizilişi elde edebiliriz. Özetle, kutuların yerlerini içlerindeki topları muhafaza ederek değiştirdiğimizde
yeni bir diziliş olmuyor. Buna karşılık, şekilde 3 numaralı topu bulunduğu kutudan alıp 4 numaralı topun olduğu kutuya koyarsak yeni bir diziliş elde ediyoruz. Çünkü eski duruma dönmek için kutuların yerlerini
içlerindeki topları muhafaza ederek değiştirmek beyhude. Topların işaretli olduğunu unutmayalım.
Boş olan kutuyu gözardı edersek şekildeki dağılımı,
\begin{align}
\nonumber
{ 1, 3 } \cup { 2 } \cup { 4 }
\end{align}
olarak yazabiliriz. Bu ayrık birleşim bize ${ 1, 2, 3, 4 }$ kümesini veriyor. Öte yandan, bu kümenin her ayrışımı, yani kesişimleri boş küme olan, ama kendileri boş küme olmayan alt kümelerin birleşimi biçiminde yazılması yukarıdaki şekildeki gibi bir dağılıma karşılık geliyor. Birleşimdeki alt kümelerin sırasını istediğimiz gibi değiştirebiliriz, bu bize yeni bir ayrışım vermez. Bu özellik, problemin ilk halinde kutuların özdeş olmasına tekabül eder. Boş olmayan alt kümelerin ayrık olması ve birleşimlerinin ${ 1, 2, 3, 4 }$ olması her topun bir ve yalnız bir kutuda olmasına karşılık gelir. Hasılı, problemin ${ 1, 2, 3, 4 }$ kümesinin farklı küme ayrışımları sayısı olduğunu görürüz.

Soruyu reküranslardan yararlanarak dolaylı yoldan çözeceğiz. Öncelikle probleme bir parametre daha ilave edelim: boş kalmayan kutu sayısı $k$. Küme ayrışımları bağlamında bu, boş olmayan ve ayrık olan alt küme sayısını $k$ olarak sabitlemek oluyor. Örneğin, ${ 1, 2, 3, 4 }$ kümesini üç alt kümeye arıştırmanın altı yolu var:
\begin{align}
\nonumber
& { 1, 2 } \cup { 3 } \cup { 4 }, \qquad { 1, 3 } \cup { 2 } \cup { 4 }, \
\nonumber
& { 1, 4 } \cup { 2 } \cup { 3 }, \qquad { 1 } \cup { 2, 3 } \cup { 4 }, \
\nonumber
& { 1 } \cup { 2, 4 } \cup { 3 } \qquad \textrm{ve } { 1 } \cup { 2 } \cup { 3, 4 }.
\end{align}

Aslında $6 = \binom{4}{2}$, bunu sayarak yorumlamak da zor değil. Fakat genel haldeki çözümde bu tatlı tesadüfü gözlemleyemeyeceğiz. Şimdi $n$ elemanlı bir kümenin, diyelim ${1, 2, \ldots, n}$, tam olarak $k$ adet boş olmayan alt kümeye ayrışımlarının sayısına $S(n, k)$ diyelim. Öncelikle $1 \leq k \leq n$ için,
\begin{align}
S(n, k) = k S(n-1, k) + S(n-1, k-1) \quad\quad\quad (7)
\end{align}
olduğunu kanıtlayacağız. Herhangi bir ayrışımda $n$ sayısının hangi alt kümede olduğuna bakalım. $n$ sayısı tek başına ${n}$ alt kümesinde de olabilir, diğer bazı sayılarla birlikte bir ${ i_1, \ldots, i_s, n }$ alt kümesinde de olabilir. İki durumda da $n$’yi sildiğimizde ${1, 2, \ldots, n-1}$ kümesinin bir ayrışımını elde ediyoruz. İlk durumda bir alt kümeyi tümden sildiğimiz için $(k-1)$ alt küme kalıyor;
ikinci durumdaysa halen $k$ adet alt kümemiz var. İlk durumdaki alt kümelerin sayısı $S(n-1, k-1)$.
İkinci durumda da $S(n-1, k)$ diyeceğiz, ama bir sorun var. İkinci durumda $n$’yi sildiğimiz anda hangi alt kümeden sildiğimizin bilgisini kaybediyoruz, kalan $k$ alt kümeden herhangi birinde olabilirdi. Tersten düşünürsek ${1, 2, \ldots, n-1}$ kümesinin bir alt küme ayrışımından ${1, 2, \ldots, n}$ kümesinin bir alt küme ayrışımına ulaşmak için ya $S(n-1, k-1)$ ile sayılan ayrışımlardan herhangi birinin yanına ${n}$ alt kümesini ilave edeceğiz, dolayısıyla alt küme sayısı $k$ olacak ya da $S(n-1, k)$ ile sayılan ayrışımların herhangi birisinde $n$’yi $k$ alt kümeden birine katacağız ki bunu yapmanın da tam olarak $k$ yolu var. Sonuç olarak $(7)$ bağıntısını birebir ve bire $k$ eşlemeler yardımıyla
göstermiş oluyoruz. Bütün $S(n, k)$’leri $(7)$ bağıntısıyla belirleyebilmek için bir de sınır değerlerine ihtiyacımız var. Bu sınır değerleri $n \geq 1$ için $S(n, 1) = 1$ (kümenin kendisini kullanmaktan başka yolumuz yok); $n \geq 0$ için $S(n, n) = 1$ (her tekli eleman bir alt kümede, boş kümenin tek ayrışımını da kendisi kabul edebiliriz) ve $S(n, n+1)$ $=S(n, n+2)$ $=\cdots$ $= 0$ ($n$ adet elemandan $n+1$ veya daha fazla boş olmayan ayrık alt küme çıkaramayız) olduğunu gözlemlemek yeterli. $S(n, 0)$ ise $n = 0$ için 1, diğer durumlarda sıfır olacak. Bu sınır değerleri ve $(7)$ ile $S(n, k)$ sayıları biricik belirlenir. $S(n, k)$ sayıları ikinci tip Stirling sayılarının işaretsiz hali olarak bilinir. Birinci ve ikinci tip Stirling sayıları için daha detaylı bilgi isteyen okuru Brualdi’deki 8. bölüme [4] yönlendireceğiz. İlerideki yazılardan birinde bu ikinci tip Stirling sayılarını başka bir bağlamda tekrar elde edip bir uygulamalarını da göstereceğiz.

Özdeş kutulara işaretli topların yerleştirilmesi problemine geri dönersek, $m$ adet işaretli topu $n$ adet özdeş kutuya yerleştirmenin,
\begin{align}
\nonumber
S(m, 1) + S(m, 2) + \cdots + S(m, n)
\end{align}
farklı yolu olduğunu buluruz. Dikkat edelim ki, cevabı yazarken boş kalmayan kutu sayısına göre tasnif ederek yazdık. Bu bağlamda her kutuya en fazla bir top yerleştirirsek cevap 1 (ne zaman?) veya 0 (ne zaman?); her kutuya en az bir top yer-leş-ti-rir-sek cevap $S(m, n)$’dir.

Kutular da toplar da özdeş

Bu son durumu da incelemeye somut bir örnekle başlayacağız. Diyelim ki dört özdeş topu dört özdeş kutuya yerleştireceğiz. Bir diziliş,

olarak verilir. Burada herhangi iki topun veya herhangi iki kutunun içindeki topları muhafaza ederek
yerlerini değiştirmekle yeni bir diziliş elde edemiyoruz, yani

dizilişi de aslında bir öncekiyle aynı. Dolayısıyla, kutuların işaretli topların özdeş olduğu durumdaki gibi her bir kutuda kaç top olduğu bizim için önemli. Bunun üzerine bir de kutuların yerlerini içindeki topları muhafaza ederek değiştirebildiğimizden içinde en çok top olan kutuyu en başa, kalanların arasında içinde en çok top olan kutuyu onun yanına, $\ldots$ alarak her yerleşimi daha standart bir hale getirebiliriz. Böylece yukarıdaki iki şekilde de diziliş $2+1+1+0$ tamsayı parçalanışına denk gelir.

Tamsayı parçalanışlarından yazının ilk bölümünde bahsetmiştik. Aslında burada kutu sayısı da belirli olduğu için bir kısıtlı parçalanış var. Genel halde, yani $n$ adet özdeş topu $m$ adet özdeş kutuya yerleştirmek için $p(n, m)$ farklı yol, yani $n$ sayısını en fazla $m$ kısım kullanarak parçalamanın farklı yolu kadar yol var.

Kısıtlı parçalanışlar için de ikinci tip Stirling sayılarının işaretsiz halleri için yaptığımız gibi bir rekürans bulup kanıtlayabiliriz. Hatta, parçalanış sayısı $p(n)$’den farklı olarak $m$’yi sabitlediğimizde $p(n,m)$ sayılarının üreteç fonksiyonunun,
\begin{align}
\nonumber
\sum_{n \geq 0} p(n, m) q^n
= \frac{1}{ (1 – q) (1 – q^2) \cdots (1 – q^n) }
\end{align}
olduğunu gösterebiliriz. Rasyonel üreteç fonksiyonlar hakkındaki gözlemlerimize binaen, $p(m, n)$’nin kapalı bir formülü olduğunu çıkarsayabiliriz. Bu bahsi daha çok uzatmayacağız, fakat ilgili okuru Andrews-Eriksson’un [1] 6. bölümünü okumaya davet ediyoruz. Şu kadarını söyleyelim ki $m$ arttıkça bu formüller korkunçlaşmaktadır ve her $m$ için çalışan kapalı bir formül halen bulunamamıştır.

Kaynakça:
[1] Andrews, G.E. and Eriksson, K., 2004. Integer partitions. Cambridge University Press.
[2] B´ona, M., 2022. Combinatorics of permutations. CRC Press.
[3] Bringmann, K. and Ono, K., 2007. An arithmetic formula for the partition function. Proceedings of the American Mathematical Society, 135(11), pp.3507–3514.
[4] Brualdi Richard, A., 2010. Introductory Combinatorics.
[5] Gasper, G., Rahman, M. and George, G., 2004. Basic hypergeometric series (Vol. 96). Cambridge university press.
[6] Hardy, G.H. and Ramanujan, S., 2000. Asymptotic formulæ for the distribution of integers of various types [Proc. London Math. Soc.(2) 16 (1917), 112–132]. Collected papers of Srinivasa Ramanujan, pp.245–261.
[7] Petkovsek, M., Wilf, H.S. and Zeilberger, D., A = B, CRC Press.
[8] Rademacher, H., 1937. A convergent series for the partition function p(n). Proceedings of the National Academy of Sciences, 23(2), pp.78–84.
[9] Stanley, R.P., 2011. Enumerative Combinatorics Volume 1 second edition. Cambridge studies in advanced mathematics.