Yazar: Sibel Kazak
Yıl: 2022-3
Sayı:113
Olasılık kuramı, belirsizlik durumlarında öngörüde bulunmamıza ve rastlantısallıkları değerlendirirken akılcı düşünmemize yardımcı olur [1]. Çeşitli bilim alanlarından günlük yaşantımıza belirsizliğin ve rastlantısallığın olduğu her yerde (sağlık, çevre, ekonomi, genetik, meteoroloji, spor, şans oyunları, sigorta gibi) olasılık kavramı karşımıza çıkar. Örneğin, günümüzde hastalıklara erken teşhis konulmasından, sürücüsüz araçların çalışmasına kadar çeşitli alanlarda uygulamaları olan makine öğrenmesindeki karar verme süreçlerinin temelinde koşullu olasılık kuramı vardır. Ya da internet işlemleriniz için güçlü bir şifreye ihtiyacınız olduğunda, doğum yılınız yerine rastlantısallığı kullanarak şifrenizi belirleyip, daha güvenli bir şekilde kişisel işlemlerinizi gerçekleştirebilirsiniz. Dolayısıyla olasılık bilgisi hayatın değişik alanlarında önemli bir role sahiptir.
Olasılık ve şansla ilgili ilk fikirler antik çağlardan beri var olsa da matematiğin bir dalı olarak olasılık kuramının gelişmesi 17. yüzyılın ortalarında Pascal ve Fermat’nın şu kumar sorusu hakkında aralarında başlayan karşılıklı mektuplaşmalar üzerine başlamıştır (daha detaylı bilgi için Matematik Dünyası’nın 2014-II sayısındaki “Olasılık Kuramının Gelişimi-I” yazısı incelenebilir): Bir çift hilesiz zarı 24 kere attığımızda en az bir 6-6 geleceğine dair bahse girmek kârlı mıdır? Bir başka deyişle, 24 atışta en az bir 6-6 atma olasılığı nedir? Bugün temel olasılık bilgisiyle kolayca hesaplayabileceğimiz bu problemin çözümü okuyucuya bırakılmıştır.
Olasılık kuramının tarihsel gelişim sürecindeki uygulamalarına bakıldığında olasılık kavramına dair çeşitli yorumlarının olduğu görülmektedir. Matematik öğretim programlarında teorik olasılık olarak adlandırılan klasik olasılık yorumuna göre bir olayın olasılığı, rassal bir deney sonucunda istenen olaydaki çıktıların sayısının tüm eş olası çıktıların sayısına oranıdır. Örneğin, iyi karılmış bir iskambil destesinden rasgele çekilen bir kartın kupa olma olasılığı 13/52’dir, çünkü bir destedeki 52 kartın on üçü karo grubundandır. Klasik olasılık rassal deneyin tüm olası sonuçlarının eş olasılıklı olduğu sonlu bir örnek uzayın olması esasına dayanır. Öte yandan olasılık kavramının 1660’larda ortaya çıkışında çifte anlam taşıdığı görülmektedir [2]. Buna göre olasılık, bir taraftan kişisel bilgi veya kanıta göre bir önermeye ne derece inanıldığıyla ilgiliyken diğer taraftan bir olayın bazı çıktılarının uzun vadede belirli bir değer etrafında sabitlenmesi fikrine dayanmaktadır. Bir başka deyişle, ilkindeki inanç anlamında olasılık ne bildiğimize dayalı olarak belirsiz bir önerme hakkında ne dereceye kadar emin olabileceğimizi düşünmeyi sağlamaktadır [3] ve kişisel (öznel) olasılık yorumuyla ilişkilidir. Örneğin, “Dinozorların sonunun devasa bir meteroitin dünyaya çarpmasından sonra tükendiğine çok eminim” ifadesinde bunu söyleyen kişinin kendi kişisel inanç derecesi ortaya konulmuştur ve “Bu olasılık yaklaşık 0,9’dur” ifadesi kişisel olasılık fikrini yansıtır [3]. Burada bahsedilen kişisel olasılığın tamamen öznel olduğu düşünülmemelidir, zira tutarlı olmak için kişisel olasılıkların olasılığın temel kurallarına uyması gerekmektedir [3]. Sonraki frekans anlamına göre de olasılık aynı koşullarda tekrarlanan deneylerde belirli çıktılarının hangi göreli sıklıkla gözlemlendiğini düşünmemizi sağlamakta [3] ve bağıl sıklık olasılık yorumu ile ilgilidir. Örneğin, bir fabrikada üretilen bataryaların %98’inin testte hatasız çıktığı verilmiş olsun. Eğer ürünlerden rasgele bir batarya seçilip test edilirse frekans yaklaşımından bakıldığında hatalı olma olasılığı %2’dir.
Okul çağında öğrencilerin olasılık kavramına ilişkin anlayışlarını geliştirmek önemlidir. Avustralya, İrlanda ve Yeni Zelanda gibi ülkelerde olasılık ve şansla ilgili temel fikirlerin öğretimine ilkokuldan başlayarak yer verilirken, ülkemizde mevcut matematik öğretim programlarında [4, 5] olasılık ilk olarak eş olası çıktılara sahip basit olaylarla sınırlandırılarak 8. sınıfta ele alınmaktadır. Bir başka deyişle, ortaokuldaki olasılık hesaplamaları bir deneyin farklı her bir sonucunun eş ölçüde olabilir (eşit şanslı) olduğu ve daha fazla parçalara ayrılamayacak bir olayın olasılığı hakkındadır. Ortaöğretim düzeyindeyse 10. sınıfta eş olasılıklı olan ve olmayan ile ayrık olan ve olmayan durumlar için basit olayların olasılıkları üzerinde durulurken 11. sınıfta koşullu olasılık, bileşik olayların gerçekleşme olasılığı ile deneysel ve teorik olasılıkların ilişkilendirilmesi yer almaktadır. Buradaki bileşik olaylar iki veya daha fazla basit olayı gerektiren deneyler sonucunda gerçekleşir.
11. sınıfta öğrencilerin ilişkilendirmeleri beklenen teorik olasılık ve deneysel olasılık, olasılık kavramının tarihsel süreçte ortaya çıkan klasik olasılık ve bağıl sıklık olasılık yorumlarına dayanmaktadır. Kişisel olasılık yorumu (öznel olasılık) ise bir olasılık çeşidi olarak ülkemizde 2005 yılından 2013 yılına kadar kullanılan ilköğretim matematik öğretim programlarında [6, 7] yer almıştır. İlkokuldan itibaren öğrencilerin olasılıkla ilgili sezgilerinden yola çıkarak kişisel olasılık kavramını geliştirmeleri için fırsatlar olmasına rağmen öğretim programlarında öğrencilerin olasılıkla ilgili bu tür kişisel yargılarda bulunurken hangi bilgileri kullanmaları üzerine odaklanılmadığı için matematik öğretim programlarında henüz gereken ilgiyi görmemektedir. Ancak 8–11 yaş arası çocuklarla yapılan araştırmalar deneysel veriler ışığında olasılıkların güncellenmesi yaklaşımıyla kişisel olasılık fikrinin gelişiminin desteklenebileceğini göstermektedir [8, 9]. Ayrıca gelişen bilgi işleme teknolojileri sayesinde üniversite düzeyinde Bayesçi istatistik yaklaşımına artan ilgiyle [10] beraber kişisel olasılık yorumunun matematik öğretim programlarında da yer alması fikri [11] giderek güçlenmektedir.
Bu yazıda olasılığın inanç ve frekans anlamlarının ilişkilendirilerek teknoloji yardımıyla öğrencilerin kişisel olasılıkla ilgili akıl yürütmelerini destekleyecek bir öğretim yöntemi sunulacaktır. Bileşik olayların olasılığına yönelik bir problemin çeşitli varyasyonları üzerinden açıklanacak olan bu yöntem, öğrencilerin sınıf düzeyine ve sahip oldukları ön bilgilere göre farklı problem durumları için uyarlanabilir. Aşağıda tanıtılan problem, bahsedilecek olan yöntemle daha önce sadece basit olayların olasılığını teorik ve deneysel olarak hesaplama bilgisine sahip olan üç farklı öğrenci (10–12 yaş) grubuyla denenmiştir [8]. Öğrencilerin genel olarak sezgilerine dayalı ilk tahminlerinin ve gerekçelerinin hatalı olduğu görülmüş, ancak yeni veriler ışığında öğrencilerin mevcut varsayımlarına ilişkin kişisel inanış değerlendirmeleri sonucunda kişisel olasılıklarını geliştirme eğiliminde oldukları gözlemlenmiştir. Şimdi bu öğrencilerin yanıtlarından örneklerin de sunulacağı problemi inceleyelim.
Problem: “Eşleştir, kazan oyunu” – İçinde kırmızı ve mavi renkli pulların olduğu 2 torba var. Oyunu oynamak için her bir torbadan rasgele bir pul çekeceksiniz. Eğer iki pul aynı renkse oyunu siz, farklı renklerdeyse rakibiniz kazanacak. Aşağıdaki durumlar için oyun adil midir?
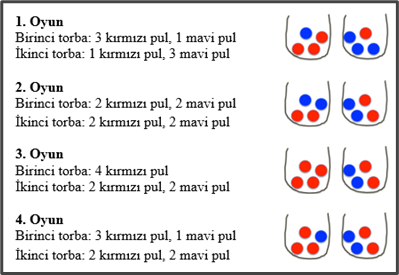
Derse girişte problemin sunuş şekli farklı sorularla zenginleştirilebilir. Örneğin, oyunun kuralı verildikten sonra öğrencilere “Kazanmak için bu oyunlardan hangisini oynamayı tercih edersiniz?”, “Kazanma şansı en düşük olan oyun hangisidir?” gibi sorular yöneltilerek gerekçeleriyle birlikte sınıfta tartışmaları istenebilir. Ayrıca bu tahminleri yaparken Görsel 1’de verilen oyunları dijital platformda oynayarak gözlemler yapmalarına olanak sağlanabilir.
Öğrenciler 2-3 kişilik gruplara ayrılarak oyunun kuralları tanıtıldıktan sonra yukarıda verilen sıraya göre her bir oyunu öğrencilerin “Tahmin”, “Somut Materyallerle Oyun Verileri Toplama” ve “Simülasyonla Oyun Verileri Toplama” olarak üç aşamada yöneltilen sorularla incelemeleri istenir. Bu üç aşamalı yaklaşım ve her aşamada sorulan sorular inanç anlamında olasılıkları özel olarak kullanan Bayesçi düşüncedeki deneyimden öğrenme modeline, yani yeni veriler ışığında kişisel olasılıkların kalibre edilmesine, göre tasarlanmıştır [12].
Dikkat ederseniz problemde oyunun adil olup olmadığı, yani her iki tarafın oyunu kazanma şansının eşit olup olmadığı sorulmaktadır. Böylelikle öğrencilerin bir varsayım hakkındaki kişisel inanç derecelerini ifade ederek olasılıksal akıl yürütmeleri beklenmektedir. Genelde matematik derslerinde bir olayın meydana gelme olasılığıyla ilgili sorularla uğraşılır. Bununla birlikte bir önermenin (varsayımın) doğru olma ihtimali de olasılık hakkında soru sormanın bir yoludur [4]. Bunun, olasılığın inanç anlamıyla ilişkilendirilerek öğrencilerin kişisel olasılıkla ilgili akıl yürütmelerinin nasıl desteklenebileceği aşağıdaki öğretim aşamalarında açıklanacaktır.
1. Tahmin Aşaması:
Öğrencilerden gruplarında sırayla her bir oyunu tartışıp, adil olup olmadığı hakkında bir tahmin yapmaları ve bunun gerekçesini açıklamaları istenir (Görsel 2). Henüz bileşik olayların olasılığını hesaplama deneyimi olmayan öğrenciler için bu tahmini yaparken olasılıkla ilgili ön bilgilerini veya sezgilerini kullanmaları beklenir. Sizce öğrenciler birinci oyunun adil olduğunu mu, olmadığını mı düşünürler? Her iki torbanın da içeriğine bakarak toplamda eşit miktarda kırmızı ve mavi pul olduğunu gören öğrenciler toplamsal akıl yürütmeyle iki tarafın da kazanma şansının eşit olduğunu, yani oyunun adil olduğunu düşünme eğiliminde olacaklardır. Peki üçüncü oyun için hangi varsayımda bulunurlar? Benzer toplamsal akıl yürütmeyle bu sefer üçüncü oyunun adil olmadığını düşüneceklerdir; çünkü toplamda kırmızı pul sayısı mavi pul sayısına göre oldukça fazla görülmektedir. Bu örneklerden sonra Görsel 1’deki diğer oyunlar için öğrencilerin ilk varsayımları hakkında tahminler yürütebilirsiniz sanırım.

Öğrencilerin tahminlerinin ardından, grupça tartışarak bu varsayımları hakkında ne derece emin olduklarını ifade edebilmeleri için kendilerinden tahminlerindeki güvenirlik düzeyini %0–%100 ölçeğinde (bak. Görsel 2) işaretlemeleri istenir. Bu yolla öğrencilerin ilk varsayımlarının (ör. oyun adildir) doğruluğuna ne kadar inandıkları görülebilir. Yukarıda bahsedilen gerekçeyle birinci oyunun adil olduğunu düşünen öğrencilerin bu varsayımın doğruluğundan oldukça emin olduğu (%80-%95) gözlemlenmiştir, fakat gerekçelerine duydukları güvene bağlı olarak kişisel inanış dereceleri belirli bir aralıkta farklılık göstermiştir. Üçüncü oyun için de oyunun adil olmadığı varsayımına dair öğrencilerin güvenirlik düzeyleri %70-%100 gibi daha geniş bir aralıkta değişim göstermiştir.
2. Somut Materyallerle Oyun Verileri Toplama Aşaması:
Öğrencilerden, her bir oyun için hazırlanmış kese kâğıdından torbalarla, oyunları istedikleri kadar oynayarak ilk tahminlerini test etmeleri istenir. Görsel 3’teki gibi oyunu kaç kez oynayacakları öğrencilere bırakılarak, kaç denemede oyunun adil olup olmadığı varsayımına ilişkin görüşlerinde bir değişim olup olmadığı ve buna bağlı olarak kişisel inanış derecelerinin nasıl değiştiği görülebilir. Bu aşamada öğrencilerin 5 ile 30 arasında deneme yaptıkları görülmüştür. Fiziksel olarak oyunun oynanışı göz önününde bulundurulursa 20–30 deneme makul denilebilir. Ama bazı öğrencilerin çok az sayıda denemeyle de yetineceklerine dikkat edilmelidir. Bu noktada olasılığın frekans anlamı da devreye girmektedir. Ancak burada verilerin rolü, öğrencilerin varsayımlarına ilişkin inanç derecesiyle ifade ettikleri, kişisel olasılıklarını mevcut kanıta (oyun verilerine) bağlı olarak değerlendirmelerini sağlamaktır.
Bu aşamada öğrenciler yeni veriler ışığında ilk varsayımlarını tekrar gözden geçirirler. Deneme sayısı az olsa da çıkan sonuçlara göre öğrencilerin tahminlerini değiştirdikleri gözlemlenmiştir. Örneğin, birinci oyunda aynı renkte kazanma (11) ve farklı renkte kazanma (19) ve üçüncü oyunda aynı renkte kazanma (3) ve farklı renkte kazanma (5) sonuçlarına göre bir grup ilkinde oyunun adil olduğu diğerindeyse olmadığı varsayımlarını değiştirmiştir. Tekrar öğrencilerin güvenirlik düzeyini %0–%100 ölçeğinde işaretlemeleri istendiğinde oyun sonuçlarından ne kadar ikna olduklarına göre kişisel inanç derecelerinde değişimler olduğu gözlemlenmiştir.

Özellikle üçüncü ve dördüncü oyun için öğrencilerin değişen varsayımlarıyla ilgili güvenirlik düzeylerinin düşme eğiliminde olduğu görülmüştür. Birinci oyundaysa varsayımlar değişse bile öğrencilerin kişisel inanç dereceleri öncekiyle aynı olarak kalmıştır.
3. Simülasyonla Oyun Verileri Toplama:
Öğrencilerin ikinci aşamadaki mevcut varsayımlarını kolay yoldan biraz daha test edebilmeleri için bilgisayar simülasyonu kullanılır. Bu yolla hızlı bir şekilde çok daha fazla denemeyle oyun sonuçlarına ulaşılabilir. Bunun için eğitici bir dinamik veri analizi yazılımı olan ve rassal deneyleri modelleme özelliğine sahip Tinker-Plots kullanılabilir. Tinker-Plots, özellikle ortaokul öğrencileri için geliştirilmiş ve öğrencilerin düşünme biçimlerine göre tasarlanmış olup, aşamalı veri organizasyonu (ayrıştırma [seperate], sıralama [order], istifleme [stack]) ile öğrencilere kendi grafiklerini oluşturmalarını ve çeşitli olasılık durumlarını modelleyerek simülasyon yoluyla verilere dayalı olasılık tahminleri yapabilmelerini sağlayan bir yazılımdır.
Görsel 4’teki TinkerPlots ile üçüncü oyundaki torbaların modellemesi solda görülen Örnekleyici’de (Sampler) iki karmaç (Mixer) aracı kullanılarak yapılmıştır. Bir torbada iki kırmızı (K) ve iki mavi (M) top, diğerindeyse dört kırmızı (K) top vardır. Sampler’daki ‘‘Repeat’’ yani simülasyonu tekrar etme sayısı 10000 olarak belirlenmiştir. Sampler’ın sağındaki tablo her tekrar sonucunu hem ayrı ayrı (Torba 1 ve Torba 2) hem de bileşik (Join) olarak (“K,K”, “M,K” gibi) göstermektedir. En sağdaki grafikse 10000 denemeli simülasyondan elde edilen bileşik çıktıların yüzdelerini (aynı renkte %49 ve farklı renkte %51) göstermektedir. Soldaki sütun “K,K” ve “M,M” çıktılarının birleştirilmesiyle (aynı renkte olanlar), sağdaki sütunsa “K,M” ve “M,K” çıktılarının bir araya (farklı renkte olanlar) getirilmesiyle oluşturulmuştur.
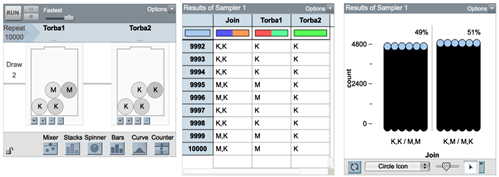
Görsel 5’teki simülasyonla oyun verileri toplama aşamasına geçildiğinde TinkerPlots kullanım deneyimi olan öğrenciler problemde verilen oyunları kendileri modelleyebilir. İkinci aşamada bahsedilen gerekçeyle burada da kaç deneme yapacakları öğrencilere bırakılmıştır. Öğrencilerin simülasyon denemeleri 100 ile 100.000 arasında değişse de çoğunlukla 100 deneme varsayımlarını desteklemek için öğrencilerce yeterli olarak görülmüştür.

Bu aşamada, beklenildiği üzere daha çok denemeden elde edilen yeni sonuçlar ışığında öğrencilerin mevcut hatalı varsayımlarını değiştirdikleri gözlenmiştir. Özellikle az sayıdaki verilere dayalı olarak ikinci aşamada üçüncü oyunun adil olduğu sonucuna varamayan öğrenciler TinkerPlots simülasyon sonuçlarından sonra varsayımlarını değiştirebilmiştir. Burada sadece çok sayıda deneme sonuçlarının değil, aynı simülasyonu birden fazla kez yaparak bağıl sıklıklardaki değişimin/sabitlenmenin gözlemlenmesi de öğrencilerin hem bağıl sıklık olasılık yorumunu anlamalarını hem de eldeki kanıtlara göre kişisel inanç derecelerini uygun şekilde revize edebilmelerini sağlayacaktır. Öğrencilerin kişisel güvenirlik düzeylerindeki pozitif değişime bakıldığında, mevcut varsayımları doğruyken simülasyon verilerinin kanıt olarak kişisel inanç derecelerine etkisinin mevcut varsayımlarını hatalıdan doğruya değiştirdikleri durumlara göre biraz daha yüksek olduğu görülmüştür. Bunun, mevcut varsayımı destekleyen yeni kanıtlar ışığında o varsayıma ilişkin kişisel olasılıkların geliştirilmesine katkı sağladığı söylenebilir.
Bu yazıda üç aşamalı (“Tahmin”, “Somut Materyallerle Oyun Verileri Toplama” ve “Simülasyonla Oyun Verileri Toplama”) öğretim yöntemiyle şansa dayalı oyunların adil olup olmama bağlamında öğrencilerin bir varsayım hakkındaki kişisel olasılıklarını yeni veriler ışığında değerlendirerek olasılıksal akıl yürütmelerinin nasıl desteklenebileceği ele alınmıştır. Bu yolla öğrencilerin erken yaşlardan itibaren olasılıkla ilgili sezgilerinden yola çıkarak kişisel olasılık kavramını geliştirmelerine olanak tanıyıp, yaşamın her alanında karşılaşılan olasılık kavramına dair daha zengin ve güçlü fikirlere sahip olmaları sağlanabilir. Bu süreçte kullanılan simülasyon araçlarının, öğrencilerin olasılıkla ilgili fikirlerini kolayca test etmeleri ve bunlar üzerinde tartışarak olasılığın farklı anlamlarını birbiriyle ilişkilendirmelerindeki rolü oldukça önemlidir. Siz de bu yöntemle sınıfınızda olasılık öğretimine yeni bir açıdan yaklaşarak öğrencilerin hem kavramsal hem de aktif olarak öğrenmelerini destekleyebilirsiniz.
Kaynaklar
[1] Rosenthal, J. S. (2016). Başıma yıldırım düştü! Olasılıkların ilginç dünyası. Çev. Kerem Keskiner. Ankara: TÜBİTAK Popüler Bilim Kitapları.
[2] Hacking, I. (1975). The emergence of probability. London, UK: Cambridge University Press.
[3] Hacking, I. (2015). Olasılık ve tümevarım mantığına giriş (1. Basım). Çev. İrfan Özdabak. İstanbul: Alfa yayınları.
[4] T.C. Milli Eğitim Bakanlığı (2018). Matematik öğretim programı (ilkokul ve ortaokul 1, 2, 3, 4, 5, 6, 7 ve 8. sınıflar).
[5] T.C. Milli Eğitim Bakanlığı (2018). Ortaöğretim matematik dersi (9, 10, 11 ve 12. sınıflar) öğretim programı.
[6] T.C. Milli Eğitim Bakanlığı (2005). İlköğretim matematik dersi 6–8. sınıflar öğretim programı.
[7] T.C. Milli Eğitim Bakanlığı (2009). İlköğretim matematik dersi 6–8. sınıflar öğretim programı ve kılavuzu.
[8] Kazak, S. (2015). A Bayesian inspired approach to reasoning about uncertainty: ‘How confident are you?’ In K. Krainer & N. Vondrová (Eds.) Proceedings of the Ninth Congress of the
European Society for Research in Mathematics Education (CERME9). Prague, Czech
Republic: Charles University in Prague, Faculty of Education and ERME.
[9] Kazak, S. & Leavy, A. (2018). Emergent reasoning about uncertainty in primary school children with a focus on subjective probability. In A. Leavy, M. Meletiou-Mavrotheris, & E. Paparistodemou (Eds.), Statistics in early childhood and primary education. Early mathematics learning and development (37–54). Singapore: Springer.
[10] Dogucu, M., & Hu, J. (2021). The current state of undergraduate Bayesian education and recommendations for the future. arXiv preprint arXiv:2109.00848.
[11] Chernoff, E. J. (2014). Will the real Bayesian probability please stand up!? In K. Makar, B. de Sausa, \& R. Gould (Eds.), Proceedings of the 9th International Conference on Teaching Statistics. Flagstaff, AZ, USA. Voorburg: International Statistical Institute.
[12] Kazak, S. (2017). Akran konuşması ve teknoloji kullanımı aracılığıyla öğrencilerin olasılıksal akıl yürütmelerinin desteklenmesi. 3. Türk Bilgisayar ve Matematik Eğitimi (TÜRKBİLMAT-3) Sempozyumu Bildiri Kitabı (s.47-58). Afyon, 17-19 Mayıs 2017.

