Galois Grupları

Yazar: Olcay Coşkun (olcaycoskun@gmail.com)

Yıl: 2022-2

Sayı: 112

Galois teorisi matematiğin en temel ve en estetik teorilerinden birisidir. Galois’nın yaklaşımı problemlere bakış açımızda köklü bir değişiklik önererek cebirin (ve matematiğin) yönünü değiştirmiştir.

Her ne kadar günümüzde ileri matematik sayılsa da Galois’nın teorisi aslında çok temel bir gözlemi ifade etmektedir. Hepimiz polinomların karmaşık köklerinin ikililer hâlinde geldiğini biliriz: Eğer $a + ib$ kökse $a-ib$ de köktür. Peki neden? Burada $i$ ile sanal birim elemanı yani, $x^2 + 1$ denkleminin bir kökünü gösteriyoruz. Gerçel sayılarda pozitif sayılar kare sayılardır, ama karmaşık sayılarda her sayı bir karedir; bu nedenden dolayı karmaşık sayılarda $i$ ile $-i$ arasında (sadece toplama ve çarpmayı kullanarak) bir ayrım yapılamaz. Dolayısıyla (gerçel sayı katsayılı) polinomlar bu değişimi göremez. Bu sebepten de $i\leftrightarrow -i$ simetrisi altında birbirine gönderilen sayılardan sadece birini kök olarak kabul edemezler.

İşte Galois’nın teorisi bu gözlemi genelleştirip, verilen bir polinom için, bir anlamda yerel olarak, o polinomun fark edemeyeceği değişimleri belirlemeyi hedeflemektedir. Örneğin, $a^2 – 2$’nin kökleri olan $\sqrt{2}$ ve $-\sqrt{2}$ ya da $a^2 + a + 1$’in kökleri $e^{2\pi i /3}$ ve $e^{4\pi i/3}$ de yukarıdakine benzer birer simetriye sahiptirler.

Bu yazının amacı Galois’nın teorisinin tam bir sunumunu yapmak değil, bu köklü değişimin ana aracı sayılabilecek Galois gruplarını tanımlamaktır. Böylece teknik ayrıntılardan uzak durmayı ve daha geniş bir okuyucu kitlesine ulaşabilmeyi hedefliyoruz. Tam bir incelemeyi ilerleyen sayılarda bir kapak konusu olarak sunmayı planlıyoruz.

Biraz tarih

Polinomların köklerinin bulunması antik bir problemdir. Binlerce yıl öncesinden ikinci derece denklemlerin çözümlerini içeren kalıntılar bulunmaktadır. Kökleri bulma probleminin yanı sıra kökleri belli bir kurala göre bulma yöntemi de ayrı bir problem olarak karşımıza çıkar. Bu yazının konusu, kökleri polinomun katsayılarıyla ifade eden formüller bulma problemi hakkında. Ancak formülleri bulurken katsayılarla birlikte sadece $+, -, \times, /$ işlemlerini ve kök almayı kullanabiliriz. Bu tür formüllerle verilen çözümlere radikal çözümler diyeceğiz. Dolayısıyla ilgilendiğimiz problemi aşağıdaki gibi ifade edebiliriz:

İkinci derece denklem içeren problemleri M.Ö. 1700’ler-den kalma Babil tabletlerinde bulunmaktadır. Babilliler $x+ y = b,\, x\cdot y = c$ formundaki denk-lem sistemlerini çözmüşlerdir. Bu denklem sistem-leri, geometrik anlamda, çevresi ve alanı verilen bir dikdörtgenin kenar uzunluklarını belirleme problemi olarak yorumlanabilir. Çözüm bugün kullandığımız formülle değil, değişken değiştirmeyle denklemi $x^2 = r$ formuna dönüştürerek yapılıyordu.

Daha yeni olan üçüncü ve dördüncü derece denklemler için olan çözümler 16’ncı yüzyılda bulunmuştur. Aşağıda bu çözümlerden birine kısaca göz atacağız.

Beşinci ve daha üst dereceli polinomlar için benzer formül arayışı uzun yıllar devam etmiştir. Birçok matematikçinin ilgisini çeken bu problemin yanıtının olumsuz olması beklenirken, hemen hemen eksiksiz ve olumsuz ilk yanıtı 1799’da Ruffini vermiştir. Ruffini’nin yanıtındaki boşlukları 1824 yılındaki yayınında Abel doldurmuş ve beşinci dereceden polinomların radikallerle çözülemeyeceğini kanıtlamıştır.

Diğer taraftan, Gauss’un hesaplarıyla gösterdiği ve Lagrange’ın genişlettiği sonuçlar bazı tür polinomların radikal çözümlerinin mümkün olduğunu göstermektedir. Dolayısıyla Abel’in teoremi yeni bir problem ortaya atmıştır:

Abel’in bu problem üzerinde çalıştığı bilinmektedir ancak çalışmasını tamamlayamadan, genç yaşta (27) tüberküloz hastalığından hayatını kaybetmiştir.

Galois bu yeni problemi, yine çok genç bir yaşta (18) çözmüş, ama ne yazık ki çözümünün kabul edilmesini göremeden bir düelloda, 21 yaşında, hayatını kaybetmiştir. Başlangıçta çeşitli gerekçelerle kabul edilmeyen Galois’nın çalışması 15 yıl sonra Liouville tarafından gözden geçirilip matematik dünyasına (MD’ye değil!) sunulmuştur. Böylece, radikallerle çözümlerin varlığını polinomlara ilişkilendirilmiş grupların (şimdi Galois grupları diyoruz) özellikleriyle belirleyen bu muhteşem fikir aydınlığa kavuşmuştur.

11 yaşına kadar evde eğitim gören Galois sonradan Paris’teki Collége Louis-le-Grad’a devam etti. 1828 ve 1829’da École Polytechnique’e girme çabaları sonuçsuz kalınca 1829’un Ekim ayında École Préparatoire’e (sonradan École Normale Supérieure adını alacak) kabul edildi. Ancak siyasi nedenlerle Aralık 1830’da okuldan atıldı. 1831-1832 yılları arasına sekiz ay hapis de yatan Galois 31 Mayıs 1832’de bir düelloda hayatını kaybetti. [1]

Galois grupları, köklerin bir takım permütasyonlarının ürettiği gruplardır. Bu fikir, yani köklerin permütasyonlarını düşünmek, ilk Galois tarafından keşfedilmemiştir. Öncesinde Ruffini ve Abel aynı fikri kullanmış olsalar da fikrin olgunluğa ulaşması Galois’yla birlikte olmuştur.

Kısa bir kronoloji

1545: Cardano, “Ars Magna”; üçüncü (Cardano) ve dördüncü (Ferrari) derece denklem çözüm yöntemi.

16. yy: Vieta’nın çalışmalarıyla formüllerin ortaya çıkışı.

1771: Lagrange, simetriler yardımıyla bilinen formülleri bir araya getirir, benzer yöntemlerin beşinci derece için çalışmayacağını gözler.

1799: Ruffini, beşinci derece denklemler için radikal çözüm olmadığı yönünde kanıt sunar, eksik olduğundan kabul görmez.

1801: Gauss, çember (ing. cyclotomic) polinomların radikallerle çözülebileceğini gösterir.

1813: Ruffini, o zaman değilse de bugün kabul gören bir kanıt sunar.

1824: Abel, beşinci derece denklemler için radikal çözüm olmadığının (kabul edilen) ilk kanıtını yapar. Simetrileri kullanmaktadır.

1830: Galois, grup tanımını da içeren ve Abel-Ruffini teoremini genelleyen kanıtını sunar, ama kabul görmeyen bu kanıt, Galois’nın ölümüyle bir süre kaybolma tehlikesine yaşar, taa ki

1847: Liouville Galois’nın çalışmasını herkesin kabul edeceği bir formda sunana kadar. 

1930: Artin, (aradaki gelişmeleri haddimiz olmadan atlayarak) Galois’nın teorisinin modern versiyonunu ortaya koyar.

Düşük derecelerde ne oluyor?

Hepimiz ikinci derece denklemleri çözmeyi biliyoruz: $a, b$ karmaşık sayılar olmak üzere,
$$x^2 + ax + b = 0$$ denkleminin kökleri,
$$x_1 = \frac{-a + \sqrt{a^2 -4b}}{2},\quad x_2 = \frac{-a – \sqrt{a^2 -4b}}{2}$$
formülleriyle verilir. Bu çözüm binlerce yıldır bilinmektedir! Kökler,
$$x_1 + x_2 = -a,\quad x_1x_2 = b$$
eşitliklerini de sağlar.

Üçüncü ve dördüncü dereceler için de kökleri benzer şekilde veren formüller vardır. Her iki formül de 16’ncı yüzyılda ortaya çıkmıştır. İlk olarak, Cardano üçüncü derece (kübik) denklemler için, sonrasında Ferrari dördüncü dereceler için yöntemler ortaya atmıştır. Daha sonra, Lagrange bilinen formülleri birleştiren bir sonuç kanıtlamıştır. Aşağıda sadece kübik denklemlerin çözümünü anlatacağız.

Öncelikle, herhangi bir kübik denklemi standart adı verceğimiz bir biçime dönüştürelim. Bir kübik denklemin en genel formu $a_0, a_1, a_2, a_3$ karmaşık sayılar olmak üzere şöyledir:
$$a_3x^3 + a_2x^2 + a_1x + a_0 = 0$$

İlk olarak, eğer gerekliyse, $a_3$ ile bölerek
$$x^3 + a_2x^2 + a_1x + a_0 = 0$$
elde edebiliriz. Kökleri $r_1, r_2, r_3$ ile gösterirsek, Vieta Teoremi’nden $r_1 + r_2 + r_3 = -a_2$ buluruz. Eğer $y = x + a_2/3$ dönüşümü yaparsak yeni denklemin kökleri toplamı $0$ olacaktır. Dolayısıyla denklemi her zaman $a_2 = 0$ olacak şekilde düzenleyebiliriz:
$$x^3 + a_1x + a_0 = 0$$
denklemine standart kübik denklem diyeceğiz.

Elde ettiğimiz denklemi çözelim. Öncelikle $x = A + B \;$ yazarsak $x^3 = A^3 + 3A^2B + 3AB^2 + B^3$ olduğundan $x^3 – 3ABx – (A^3 + B^3) = 0$ denklemini buluruz. Yukarıdaki standart denklemle karşılaştırırsak $3AB = -a_1$ ve $A^3 + B^3 = -a_0$ buluruz. Buradan da
$$t^2 + a_0t \; – \; (a_1^3/27) = 0$$
denkleminin çözümlerinin $A^3$ ve $B^3$ olacağı ortaya çıkar. Son elde ettiğimiz denklem ikinci derece olduğundan çözebiliriz:
$$t_{1, 2} = -\frac{a_0}{2} \pm \sqrt{\frac{a_0^2}{4} + \frac{a_1^3}{27}}$$
Böylece standart kübik denklemimizin köklerini bulmuş olduk:
$$
A + B = \sqrt[3]{-\frac{a_0}{2} + \sqrt{\frac{a_0^2}{4} + \frac{a_1^3}{27}}} +
\sqrt[3]{-\frac{a_0}{2} – \sqrt{\frac{a_0^2}{4} + \frac{a_1^3}{27}}}
$$

Aslında bu son eşitlik toplamda 9 sayı tarif etmektedir (her bir küp kökün 3 değeri olacak). Ancak $3AB = -a_1$ eşitliği de sağlanmak zorunda olduğundan bu 9 değer üçe indirgenmektedir. Dikkatli bir incelemeyle, $x_1 = A + B$ iken diğer iki kökün $x_2 = \omega A + \bar\omega B$ ve $x_3 = \bar\omega A+ \omega B$ olacağı görülebilir. Burada $\omega = e^{2\pi i/3}$ birimin kübik köklerinden gerçel olmayan birini gösteriyor.

Vieta’nın Teoremi’nin kübik versiyonu, katsayıları köklerin fonksiyonu olarak belirler:

1. $x_1 + x_2 + x_3 = a_2 (= 0),$
2. $x_1x_2 + x_1x_3 + x_2x_3 = a_1,$
3. $x_1x_2x_3 = -a_0$

Verdiğimiz iki örneğin önemli iki ortak özelliğine dikkat çekelim:

Tabii ikinci gözlem temel olarak Vieta’nın Teoremi’nin bir sonucudur ve tüm derecelerden polinom denklemleri için geçerlidir. Konuyu bilenler için, bu katsayı formülleri aslında köklerin temel simetrik polinomlarından başka bir şey değil! Asıl problem ilk gözlemin ne kadar genel olduğu!

Biraz tanım

Galois’nın içgüdüsü, belki de problemin çözümünün katsayıları değil kökleri düşünerek bulunacağıydı. Galois’nın makalesinde katsayıların hiç görünmüyor olması bu içgüdüye işaret olarak düşünülebilir. Biz de bu fikri takip edeceğiz. Dolayısıyla, yazımızın geri kalan bölümü için, $r_1, r_2,\ldots, r_n$ karmaşık sayıları, rasyonel sayı katsayılı $p(x)$  polinomunun kökleri olsun. Bu kökleri ve dört işlemi kullanarak elde edebileceğimiz sayıları tarif edeceğiz. Bunun için, $P$ ve  $Q$ rasyonel katsayılı ve $n$ değişkenli polinomlar olduğunda $f = P/Q$ oranına bir rasyonel fonksiyon denildiğini hatırlayalım.  

Tanım 1.

$$\mathbb{Q}\left(r_1, r_2, \ldots, r_n\right)=\{ f(r_1, r_2, \ldots, r_n) | f=P / Q \text { rasyonel } Q(r_1, r_2, \ldots, r_n) \neq 0 \}$$

Örnek 1.

$r_1 = \sqrt{2}$ olsun. O zaman,
$$\mathbb{Q}(\sqrt{2}) = \{a + b\sqrt{2} \mid a, b\in \mathbb{Q}\}$$
olur. Gerçekten de $(\sqrt{2})^2=2$ olduğundan herhangi bir polinomun $\sqrt{2}$’de hesaplanması $a_1 + \sqrt{2}a_2$ biçiminde yazılabilir. Ayrıca $(\sqrt{2} +1)^{-1} = \sqrt{2} – 1$ eşitliği sağlanır.

Örnek 2.

$r_1 = \sqrt{2}, r_2 =\sqrt{5}$ olsun. Bu durumda,
$$\mathbb{Q}(\sqrt{2}, \sqrt{5}) = \{a + b\sqrt{2} + c\sqrt{5} + d\sqrt{10} \mid a, b, c, d\in \mathbb{Q}\}$$
olur. Bu örneğe daha sonra döneceğiz. Alıştırma olarak,
$$
\mathbb{Q}(\sqrt{2}, \sqrt{5}) = \mathbb{Q}(\sqrt{2} + \sqrt{5})
$$
eşitliğinin sağlandığını göstermeye çalışın.

Galois cisim teorisini kullanmamıştır. Modern dilde $\mathbb{Q}(\sqrt{2})$’ye $\mathbb{Q}$’nun $\sqrt{2}$ genişlemesi diyoruz. (Cisim tanımı için 70’inci sayfa sonuna bakınız.) Yukarıdaki rasyonel fonksiyon gösterimiyle ilgili dikkat edilmesi gereken iki nokta var:

• $P$ ve $Q$ polinomları seçildiğinde $P/Q$ düzgün tanımlı bir fonksiyondur. Diğer taraftan, $r_1, r_2, \ldots, r_n$’de hesapladığımızda ortaya bir karmaşık sayı çıkar ve bu sayının $(P/Q) (r_1, r_2, \ldots, r_n)$ gösterimi biricik değildir.
• Başlangıçta kökleri sıralarken ilk seçimimizden farklı bir sıralamayla başlarsak, sonuçta aynı kümeyi elde ederiz, ancak elemanları elde etme yöntemimiz değişir. Örneğin $\sqrt{5}, \sqrt{2}$ sıralamasıyla başladığımızda $P(x_1, x_2) = x_1$ polinomu $\sqrt{2}$ yerine $\sqrt{5}$ üretir.

Bu uyarılar kümenin tanımını etkilememektedir. Ancak az sonra göreceğimiz gibi köklerin permütasyonlarını tanımlarken etkili olacaklar.

Polinom kökü mü değil mi?

Bir polinomun kökü olma katsayılara bağlıdır. Eğer karmaşık sayı katsayılara izin verilirse her karmaşık sayı bir polinom kökü olur ($z$ sayısı $x – z$’nin köküdür). Katsayıların geldiği cisim büyüdükçe eski köklere yenileri eklenerek kök olabilenler arttığından ilginç olan katsayıları olabildiğince kısıtlamaktır. Örneğin, katsayıları tamsayı olan bir polinomun köklerinin her birine cebirsel sayı denir. Polinom kökleri için radikal çözüm arayışımızda tamsayı katsayılı polinomlarla, dolayısıyla cebirsel sayı olan köklerle meşgul oluyoruz. Ancak Galois’nın da not ettiği üzere, katsayıları daha büyük cisimlerden aldığımız durumda da aynı fikirler geçerliliğini korur.

Cebirsel sayılar tüm rasyonel sayıları kapsar. Ayrıca bazı irrasyonel sayılar da cebirseldir, örneğin $x^2 – 2$’nin kökü olan $\sqrt{2}$. Cebirsel olmayan (aşkın) sayıların en bilinen örnekleri $\pi$ ve $e$ sayılarıdır. Bir sayının aşkın olduğunu göstermek çoğu zaman zor bir iş olsa da gerçel sayıların hemen hemen hepsinin aşkın olduğunu biliyoruz.

Galois gruplarını tanımlamak için üç temel sonuca ihtiyacımız var. Bu sonuçların kanıtları cisim genişlemelerine ve polinom halkalarının bazı özelliklerine dayanır. Böylesine teknik bir inceleme uzun ve yoğun bir çalışma gerektirir. Bu sebepten, ihtiyaç duyduğumuz temel sonuçları kanıtsız sadece örnek üzerinde göstererek vereceğiz. Amacımız Galois’nın köklerin permütasyonu fikrini göstermek olduğundan kanıtsız ilerlemekte sorun görmüyoruz.

İlk iddiamız yukarıdaki örnekte alıştırma olarak verdiğimiz eşitliğin her zaman doğru olduğunu söylüyor. Daha açık olarak,

$\mathbb{Q}(r_1, r_2, \ldots, r_n)$ cismi içinde
$$
\mathbb{Q}(r_1, r_2, \ldots, r_n) = \mathbb{Q}(u)
$$
eşitliğini sağlayan bir $u$ bulunur,

yani, $n$ tane kök ekleyerek elde ettiğimiz tüm sayıları aslında sadece bir tane elemanla (dolayısıyla sadece bir değişkenli polinomları kullanarak) elde edebiliriz. Bu eşitliğin aynı zamanda her $i = 1, 2, \ldots, n$ için $r_i \in \mathbb{Q}(u)$ sonucunu verdiğini fark edelim. İleride kullanmak üzere, her $r_i$ için $r_i = f_i(u)$ eşitliğini sağlayan bir rasyonel fonksiyon $f_i(x)$ seçelim. Dikkat edilirse bu fonksiyonların varlığı aynı zamanda yukarıdaki eşitliğin sağlandığını da kanıtlamaktadır.

İndirgeyebildiklerimizden misiniz yoksa indirgeyemediklerimizden misiniz?

Polinomları incelerken katsayıların seçimi önemlidir. Örneğin, en rahat halimizle, katsayıların karmaşık sayılar olmasına izin verirsek, o zaman her polinomu birinci dereceden polinomların çarpımı olarak yazabiliriz. Gerçekten de $p(x)$ polinomunun kökleri $r_1, r_2, \ldots, r_n$ ise
$$
p(x) = \prod_{i=1}^n (x – r_i)
$$
olur. $r_i$’ler karmaşık sayı olduğundan $(x – r_i)$ polinomu da karmaşık katsayılıdır. Dolayısıyla başladığımız katsayılar türünden bir çarpanlara ayırma elde etmiş oluruz. Bir diğer deyişle, $p(x)$’i birinci dereceden polinomların çarpımına indirgemiş oluruz. Birinci derece polinomları sabit olmayan iki polinomun çarpımı olarak yazamayacağımız için bu polinomlara indirgenemez diyelim.

Eğer katsayıları kısıtlarsak, örneğin sadece gerçel katsayılı polinomları düşünürsek, bu durumda yukarıdaki çarpanlara ayırmaya her zaman izin vermemiş oluruz. Çünkü $r_i$ gerçel olmayan bir karmaşık sayıysa, $(x – r_i)$ gerçel katsayılı olmaz. Diğer taraftan, polinom kökleri bilgilerinizi yoklarsanız, bu tür gerçel olmayan köklerin ikililer halinde geldiğini hatırlarsınız, yani, eğer $p(z) = 0$ ise $p(\bar z) = 0$ olur. O zaman kökleri gerçel
kökler $r_1, r_2, \ldots, r_k$ ve gerçel olmayan kökler $r_{k+1}, \ldots, r_n$ olarak ikiye ayırırsak,
$$
p(x) = \prod_{i=1}^k (x – r_i)\prod_{j=1}^l(x^2 – a_j x + b_j)
$$
olarak yazabiliriz. Burada $l, a_j, b_j$’leri açık olarak belirlemek mümkün ama ihtiyacımız yok.

Bu kez indirgeyemediklerimiz birinci ya da ikinci dereceden polinomlar oldu. Bu yönde devam edip, katsayıları rasyonel sayılara kadar kısıtlarsak, artık herhangi bir dereceden indirgenemez polinomlar ortaya çıkmaya başlayacaktır. Örneğin $x^3 + x + 1$ polinomunu rasyonel katsayılı ve sabit olmayan iki polinomun çarpımı olarak yazamayız.

Örnek 3.

Yukarıdaki örneğe döneceğiz, yani $r_1 = \sqrt{2}, r_2 = \sqrt{5}$. Polinom kökleriyle başlamak istediğimizi hatırlatalım. Dolayısıyla, bundan sonraki hesapların düzgün işlemesi için listemizi $r_1 = \sqrt{2}, r_2 = – \sqrt{2}, r_3 = \sqrt{5}, r_4 = -\sqrt{5}$ alalım. Tabii ki bu yeni elemanlar kümemize yeni sayılar eklemeyecektir. Amacımız $\mathbb{Q}(\sqrt{2}, – \sqrt{2}, \sqrt{5}, -\sqrt{5}) = \mathbb{Q}(\sqrt{2} + \sqrt{5})$ olduğunu göstermek.

Biraz hesap yapalım: $u = \sqrt{2} + \sqrt{5}$ olmasını istiyoruz. Öyleyse $\sqrt{5} = u – \sqrt{2}$ olacak. İki tarafın karesini alırsak,
$$(u – \sqrt{2})^2 = 5$$ $$ u^2 – 2\sqrt{2}u + 2 = 5$$ $$ \sqrt{2} = \frac{u^2 – 3}{2u}$$
buluruz. Dolayısıyla $f_1 (x) = \frac{x^2 – 3}{2x}$ yazdığımızda $\sqrt{2} = f_1(u)$ eşitliği sağlanır. Şimdi kolayca $f_2 (x) = -f_1(x)$ tanımlayabiliriz. Diğer iki kök için de $\sqrt{2} = u – \sqrt{5}$ eşitliğini kullanıp benzer işlemler yaparsak $f_3 (x) = – f_4(x) =
\frac{x^2+3}{2x}$ rasyonel fonksiyonlarını buluruz.

Kanıtı zor ikinci iddiamızsa

$\mathbb{Q}(r_1, r_2, \ldots, r_n)$’nin her elemanı $v$ için $v$’yi kök kabul eden indirgenemez rasyonel katsayılı bir polinom bulunduğunu

söylüyor. (İndirgenemezlik için yazı içindeki ilgili kutuyu bulun!) Bir diğer deyişle, polinom kökleri $r_1, r_2, \ldots, r_n$ ile üretilmiş tüm sayılar da polinom köküdür. Özel olarak, bir önceki iddiamızın sonucu olan $u$ elemanı da indirgenemez bir polinomun kökü olmalı.

Örnek 4.

Bu iddiamızı da hemen bir önceki örnek üzerinde deneyelim. $u = \sqrt{2} + \sqrt{5}$ almıştık. Köklerinden biri $u$ olan bir polinom bulmak için $u$’nun kuvvetlerini hesaplayalım. Detayları okuyucuya bırakıyoruz.
$$
u^2 = 7 + 2\sqrt{10}$$ $$u^3 = 17\sqrt{2} + 11\sqrt{5}$$ $$ u^4 = 89 + 28\sqrt{10}
$$
Dikkat edilirse $u^4$ ile $u^2$ arasında rasyonel katsayılı bir ilişki kurulabilir. Şöyle ki
$$
u^4 – 14 u^2 = 89 + 28\sqrt{10} – 14(7 + 2\sqrt{10}) = -9
$$
eşitliği $u$’nun $g(x) = x^4 – 14x^2 + 9$ polinomunun bir kökü olduğunu vermektedir. Aslında yukarıdaki iddiamız $u$’nun indirgenemez bir polinomum kökü olacağını söylüyordu. Dolayısıyla $g(x)$’in indirgenemez olup olmadığını da kontrol etmeliyiz. Bu amaçla diğer kökleri belirleyelim.

Öncelikle $u_1 = u$ olsun. $g(x)$ çift polinom olduğundan $u_2 = – u_1$’de $g(x)$’in kökü olacak. Diğer iki kökün $u_3 = \sqrt{2} – \sqrt{5}$ ve $u_4 = -u_3$ olacağını okuyucu gösterebilir. Tabii $u_3$’ün kök olduğunu göstermek yeterli. Sonuç olarak,
$$
g(x) = (x – u_1)(x – u_2)(x – u_3)(x – u_4)
$$
elde etmiş olduk. Kökler rasyonel olmadığından yukarıdaki çarpanlara ayırma rasyonel katsayılı olmadı. Polinomun indirgenemez olduğunu göstermek için ikili çarpımların da rasyonel katsayılı olmadığını göstermek yeterlidir. Bunu da okuyucuya alıştırma olarak bırakıyoruz.

Şimdi örneği takip ederek, genel durumda da $u$’nun kök olduğu indirgenemez polinomu $g(x)$ ile gösterelim ve $g(x)$’in köklerini $u_1 = u, u_2, \ldots, u_m$ olarak yazalım. Böylece üçüncü ve belki de kabullenmesi en zor iddiamıza ulaştık. Yukarıda her $r_i$ için bir $f_i(x)$ rasyonel fonksiyonu seçtiğimizi hatırlayın.

Her $j = 1, 2, \ldots, m$ için,
$$
\{r_1, r_2,\ldots, r_n\} = \{ f_1(u_j), f_2(u_j), \ldots, f_n(u_j)\}
$$
eşitliği sağlanır.

Dikkat edilirse, $f_i$’lerin seçiminden dolayı, yukarıdaki eşitlik $j=1$ için aşikâr olarak sağlanmaktadır. İddiamız $f_i(x)$’lerin $u$’nun kökü olduğu polinomun diğer köklerindeki değerlerinin de $r_j$’leri (belki başka bir sırada) vereceğidir.

Örnek 5.

Yukarıda yaptığımız hazırlıkların meyvelerini toplama zamanı geldi. Bulduğumuz $f_i(x)$’leri her bir $u_j$’de hesaplayalım. Yine işlemleri okuyucuya bırakıp sonucu aşağıya not edelim:

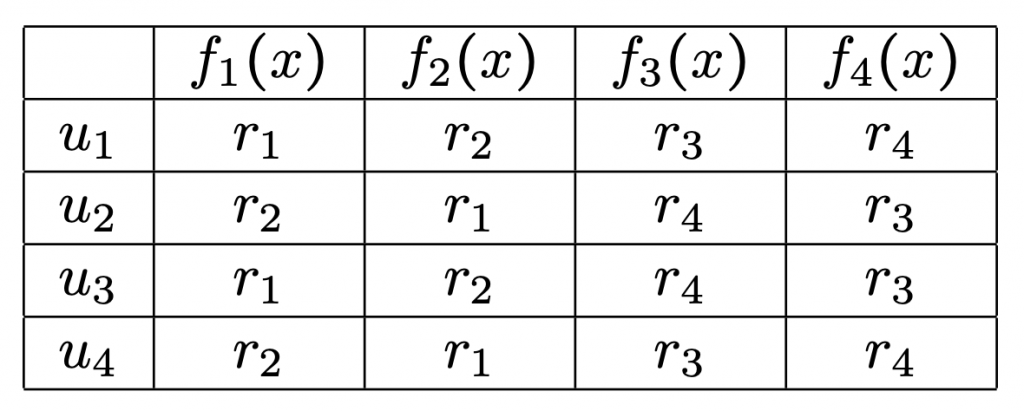
Bu noktada imkânsızı başarıp üçüncü iddianın doğruluğunu da kabul eden okuyucu Galois grubunun tanımını görebilir. Amacımız köklerin permütasyonlarını tarif etmekti. Yukarıdaki örnekte de görüleceği gibi her bir $u_j$ köklerin bir permütasyonunu veriyor. Daha açık olarak her $j = 1, 2, \ldots, m$ için
$
\pi_j \in {\text{Sym}}({r_1, r_2, \ldots, r_n})
$ permütasyonunu, $$\pi_j(r_i) = f_i(u_{j})$$ eşitliğiyle tanımlayalım ve son olarak,

kökleri $r_1, r_2, \ldots, r_n$ olan $p(x)$ polinomunun $\mathbb{Q}$ üzerindeki Galois grubu,
$$\mathcal{G}\mathcal{A}\mathcal{L}(p(x)/\mathbb{Q}) = \{\pi_j \mid j = 1, 2, \ldots, m\}$$

olarak tanımlanır.

Örnek 6.

Yukarıdaki tablodan köklerin permütasyonlarını okur ve bunları standart olarak $S_n$ içinde yazarsak,
$$
\pi_1 = \text{id}, \pi_2 = (1\,\, 2)(3\,\, 4), \pi_3 = (3\,\,4), \pi_4 = (1\,\, 2)
$$
olduğunu görürüz. Temel grup teori bilgisiyle,
$$\mathcal{G}\mathcal{A}\mathcal{L}(p(x)/\mathbb{Q})\cong V_4 (= \mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z})
$$
sonucuna ulaşabiliriz.

Şimdi durup, verdiğimiz isimlerden bağımsız olarak sonucu anlamaya çalışalım. Polinomumuzun kökleri $\sqrt{2}, -\sqrt{2}, \sqrt{5}$ ve $-\sqrt{5}$ idi. Bu köklerin sahibi $$p(x) = x^4 – 7x^2 + 10$$ polinomudur.

Permütasyonlara bakarsak, aslında sadece ilk iki kökü ve son iki kökü kendi aralarında karıştırmaya izin veriyoruz. Yani, köklerin simetrileri aslında bir dikdörtgenin simetrileriyle eşleşiyor. Bu beklentimizi karşılayan bir sonuç, çünkü
$$p(x) = (x^2 – 2)(x^2 -5)$$
olarak yazılabilir ve bu yazımdaki çarpanlar indirgenemezdirler. Dolayısıyla, parçaların köklerinin birbirinden bağımsız olmasını bekliyoruz. Çok daha ilginç iki polinom örneğini aşağıda bulabilirsiniz.

Peki ya sonra?

Kritik kanıtları yapmadan hızlıca Galois gruplarını tanımladık. Dikkat ederseniz, yukarıdaki örneğimizde, dört kökün toplam 24 permütasyonundan 4 adedini belli bir şekilde seçtik ve ortaya çıkan gruba (grup ortaya çıkması da ilginç!) Galois grubu dedik. Her şeyden önce bu grubun radikallerle çözümün mümkünatı ile ilgisinin kurulması gerekli.

Galois’nın temel sonucu da işte bu ilişkiyi kuruyor: $p(x)$ polinomunun radikallerle çözümünün olması, bu polinomun Galois grubunun belli bir özelliğe (çözülebilirlik*) sahip olmasına denktir. (MD-2013-IV sayımızda çözülebilir gruplarla ilgili temel sonuçlar bulunuyor.)

Galois teorisini kullanarak derecesi dört ve daha küçük her polinomun radikallerle çözülebileceğini formülleri bulmadan kanıtlayabiliriz. Tek yapmamız gereken bu tür polinomların Galois gruplarının çözülebilir olduğunu göstermek. Ancak en çok dört kök olacağından, köklerin bütün permütasyonlarını düşünsek bile, elde edeceğimiz grubun mertebesi en çok 24 olacaktır. Grup teori kullanarak, çözülebilir olmayan gruplardan en düşük mertebelisinin mertebesinin 60 olduğu gösterilebilir. Dolayısıyla mertebesi $\le 24$ olan tüm gruplar çözülebilirdir. Dolayısıyla, derecesi 4 ve daha düşük polinomlar için radikallerle çözüm mümkündür. Dikkat ederseniz bu kanıtı kullanıp ilk bölümde hatırlattığımız formüllere ulaşmamız mümkün değildir!

Diğer taraftan derecesi 5 veya daha büyük olan polinomlardan bir çoğunun Galois grubu çözülebilir değildir. Örneğin $x^5 -10x + 2$ polinomunun Galois grubu $S_5$’e eşittir ve dolayısıyla radikallerle çözülemez. Oysa $x^5 – x + 15$ polinomunun Galois grubu $V_4$ olduğundan radikallerle çözüm mümkündür.

Galois’nın simetrileri bildiğimiz gibi değil!

Galois’nın seçtiği kök simetrileri, köklerin geometrik yerlerine bakarak gözle karar verilebilmenin ötesindedir. Aşağıdaki iki örneğe bakalım. Sizce hangisi daha simetrik? Hangi polinom radikallerle çözülebilir?

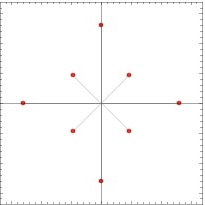
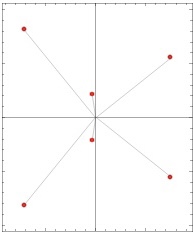
(Grafikler wolframalpha.com sayfasından alınmıştır.)

Görsel olarak incelediğimizde sağdaki resim daha simetrik görünüyor. Hem koodrinat eksenlerinde hem de $y = x$ ve $y = -x$ doğrularında yansıtabiliriz, $90^\circ$ ve katlarında döndürebiliriz, sadece içteki ya da sadece dıştaki kökleri döndürebilir ya da yansıtabiliriz vs. Diğer taraftan soldaki görsel daha az simetrik görünüyor. Örneğin $y$ ekseninde yansıma yapamayız, düzlemi döndüremeyiz vs.

Beklenen sürpriz, Galois teori yönünden, soldaki şeklin daha simetrik olduğu yönünde. Gerçekten de soldaki kökler, $$x^6 + 3x^4 – 2x^3 + 6x^2 + 1$$ polinomuna ait ve bu polinomun Galois grubu $S_5$, yani kökler oldukça simetrik! Bir diğer ilginç nokta da şekilde gözle görülebilir beşli döngü olmaması!

Diğer yandan sağdaki şekil Galois teorisi açısından simetri fakiridir. Bu görseldeki sekiz kök, $$27x^8 -72 x^4 – 16$$ polinomuna ait ve olası $8!$ permütasyona karşın Galois grubunun mertebesi sadece 16 (Galois grubu $D_{16}$, yani düzgün sekizgenin simetri grubu).

Galois teorisini, dolayısıyla cisim genişlemelerini ve polinom halkalarını, daha derinlemesine öğrenmeden bu sonucun kanıtını anlamak pek mümkün değil. Yine de Galois’nın ulaştığı sonucun yüceliğini takdir edebiliriz. Köklerin permütasyonlarından kritik bir seçim yaparak, yüzyıllar boyunca çözülemeyen bir problemi, tamamen soyut bir kavram (grup) ortaya atıp, bu soyut kavramın bir özelliğine indirgemiş ve çözmüştür.

Galois’nın ortaya attığı bakış açısı biz cebirciler için bir rol modeldir. Yaptığımız işlerde Galois’yı örnek alır, onun yarattığı teorinin benzerini bulmak isteriz. Lisans cebir derslerinden başlayarak öğrencilerimize bu yaklaşımı öğretir, cebirsel yaklaşımlarının Galois’nın teorisiyle şekillenmesini isteriz. Birçok matematikçinin de kabul edeceği üzere, Galois’dan bu yana soyut matematikte daha büyük bir keşif olmamıştır!

Yazımızı, Galois’nın düello gecesi, 29 Mayıs 1832’de arkadaşı Auguste Chevalier’e yazdığı mektubun son cümlesiyle bitirelim. Galois’nın radikallerin çözümü de dahil önemli çalışmalarını bu mektupla arkadaşına gönderdiği inancı olsa da yukarıda belirttiğimiz tarihlerden de anlaşılacağı üzere bu doğru değildir. Bu mektup Galois’nın bazı yeni keşiflerini içerse de en önemlilerini içermemektedir. Çok genç yaşta hayatını kaybeden Galois’nın yazılarının titiz ve detaylı bir incelemesi [3]’te bulunabilir. İlgilenen okurlara içtenlikle tavsiye ederiz.

Après celà il se trouvera, j’espère, des gens qui trouveront leur profit à déchiffrer tout ce gachis. Je t’embrasse avec effusion.

$E \; \underline{GALOIS}$

Bundan sonra, umarım, tüm bu karmaşayı deşifre etmekten faydalanacak insanlar olacaktır. Seni coşkuyla kucaklıyorum.

$E \; \underline{GALOIS}$

Galois’nın çalışmaları

Sur la théorie des nombres Nisan 1830.

Galois bu makalesinde sonlu cisimleri tanımlar ve bu cisimlerin temel özelliklerini inceler.

Bu makalenin dışında, Galois’nın yukarıda bahsettiğimiz mektubunda sözü geçen 3 çalışması bulunmaktadır:

Sur les conditions de résolubilité des equations par radicaux:

Bugün Premier Mémoire olarak biliniyor. Paris Academy’nin üç kere reddettiği bu çalışma Galois gruplarının tanımını ve çözülebilirlik kriterini içeriyor. Galois Theori’nin ortaya çıktığı çalışmadır. 1847’de Liouville tarafından gün ışığına çıkarıldı. Taslağın başlığını (yukarıda) ve kanıtlarından bir parçayı (aşağıda) kendi el yazısından fotoğraflarla paylaşıyoruz. Tüm notlara [4]’ten ulaşılabilir.

Second Mémoire: Galois’nın bu çalışması taslak olarak kalmıştır. Grup teorinin temellerini incelemeye gayret sarfettiği bu taslakta çözülebilir grupları da belirlemeye çalışmıştır.

Troisième Mémoire: İntegraller ve elliptik fonksiyonlar hakkında olduğunu belirttiği bu çalışma kaybolmuştur.

*: Çözülebilir gruplar ilerleyen yıllarda başka özellikleriyle de öne çıkmıştır. 1900’lerin başında Burnside çözülebilir olmayan grupların mertebesinin çift olması gerektiğini iddia etmiştir. Bu sanı 60 yıl sonra Feit-Thompson tarafından çözülmüş ve elde edilen sonuç basit sonlu grupların sınıflandırılması probleminin temel taşlarından biri olmuştur.

1. Gowers, T. et al, The Princeton Companion to Mathematics, Princeton University Press, 2008.
2. Tignol, J. P., Galois’ Theory of Algebraic Equations, World Scientific, 2001.
3. Neumann P. M., Mathematical Writings of Évariste Galois, European Mathematical Society, 2011.
4. Galois É., Manuscripts, digital images by F. Xavier Labrador at 

https://www.bibliotheque-institutdefrance.fr/sites/default/files/memoire-equations-radicaux-galois-evariste.pdf