Ahmet Feyzioğlu
Asal sayılar, $1$’den farklı ve kendisiyle $1$’den başka böleni bulunmayan pozitif tamsayılardır. Her pozitif tamsayı, asal sayıların çarpımı olarak yazılabilir, üstelik tek bir şekilde yazılabilir. Bu önermeye ”Aritmetiğin Temel Teoremi” denir.
Asal sayıların bir listesini yaparsak, tamsayılar içinde gittikçe seyreldiklerini görürüz. Acaba asal sayılar bir yerde biter mi? Yani asal sayılar sonlu mudur yoksa sonsuz mudur?
Öklid
Asal sayıların sonsuz sayıda olduğunu (M.~Ö.~300 yıllarında) Öklid’in Elemanlar‘ında okuyoruz. [IX.~kitap, 20.~Önerme.] Öklid’in ispatı, olmayana ergi yöntemine dayanır. Bu ispatın üstünden bir geçelim.
Asal sayıların $n$ tanesini ele alalım ve bunlara $p_1$, $p_2$, $\dots$, $p_n$ diyelim. $A = p_1p_2\dots p_n+1$ sayısı bu asal sayıların hiçbire bölünmeyecektir, dolayısıyla $A$ sayısının herhangi bir asal böleni, ${p_1, p_2, \dots, p_n}$ kümesindekilerden farklı bir asal sayı olacaktır. Böylece asal sayıların $n$ tane olamayacağı sonucu çıkar.
Dikkat edilirse Öklid, bugün bizim yaptığımız gibi, “sonsuz sayıda asal sayı vardır” demiyor. Sonsuz bir çokluktan bahsetmek kadim Yunan matematiğinde ve felsefesinde mümkün değildi. Öklid’in önermesi, verilen herhangi bir asal sayı listesinin dışında yeni bir asal sayı bulunabileceğini söyler.
Gene dikkat edilirse, Öklid $A$ sayısının bir asal sayıyla bölünmesini kullanıyor. [VIII.~kitap, 31.~Önerme], ama Aritmetiğin Temel Teoremi’nin bütün kuvvetini, $A$ nın asal sayılara ayrılışının tek türlü olmasını kullanmıyor.
Öklid’in ispatındaki fikir, ufak tefek değişikliklerle $4k – 1$ şeklindeki asal sayıların da sonsuz adette olduğunu ispat etmeye yarar. Benzer şekilde $3n – 1$ şeklindeki asal sayıların da sonsuz adette olduğunu ispatlayabiliriz. Ancak Öklid’den sonraki 2000 yılda ciddi bir gelişme olmadığını söylesek yeridir, ta ki Euler’e gelinceye kadar.
Euler
Leonard Euler (1707–1783), asal sayıların sonsuzluğu için Öklid’inkinden tamamen farklı bir ispat verdi. Dahiyane bir ispat… Aritmetiğin Temel Teoremi’nin tüm kuvvetini kullanan bir ispat… Bu teoremi matematiksel olarak ifade eden bir ispat…
Euler’in ispatının ana fikrini anlamak için ilk aşamada yakınsaklık meselesini göz ardı edelim. Asal sayılar üzerinden alınan $\prod \big(1 + \frac{1}{p} + \frac{1}{p^2} + \frac{1}{p^3} + \cdots\big)$ sonsuz çarpımı, $a(n)$ ile $n$’nin asal çarpanlara ayrılış sayısını gösterirsek, $\sum_{n = 1}^{+\infty} \frac{a(n)}{n}$ toplamına eşittir. Fakat Aritmetiğin Temel Teoremi, $1$’den büyük her tamsayının bir ve yalnız bir şekilde asal çarpanlara ayrıldığını söyler; başka bir ifadeyle her $n$ için $a(n) = 1$’dir, yani yukarıdaki sonsuz çarpım $\sum_{n = 1}^{+\infty} \frac{1}{n}$’dir.
Yakınsaklık ve ıraksaklığı da işin içine katarsak, harmonik seri diye bilinen $\sum_{n = 1}^{+\infty} \frac{1}{n}$ serisi ıraksak olduğundan,
$\prod \big(1 + \frac{1}{p} + \frac{1}{p^2} + \frac{1}{p^3} + \cdots\big) = \prod \big(1 – \frac{1}{p}\big)^{-1}$ ve $\prod \big(1 – \frac{1}{p}\big)$ çarpımlarının ıraksadığı ve $\sum \frac{1}{p}$’nin ıraksadığı sonucu çıkar. Dolayısıyla asal sayılar sonsuzdur.
Euler bu ispatı 1737 yılında tamamladı. Bu ispatın basıldığı 1744 tarihli makalesinde,
$$
\frac{1}{2}+ \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \cdots
= \log \log \infty
$$
eşitliğini de görüyoruz. (Yazımızda “log” doğal logaritmayı, yani $e$ tabanına göre alınan logaritmayı göstermektedir.) Euler bu eşitliğe varmak için,
$$\frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \cdots
\\
= \log\big( 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \cdots \big)
\\
= \log \log \infty$$
diye özetleyebileceğimiz bir muhakeme kullandı. Kullandığı seriler ıraksaktır. Yakınsak olmayan bütün serileri aforoz etmiş olan 19.~yüzyıl matematiği, Euler’in muhakemesini doğru bulmadı. Oysa Euler’in fikrinin yüceliği yanında yakınsaklık-ıraksaklık tartışması çok sığ kalır, zaten $p$ yerine $p^s$ ($s > 1$) yazmak her şeyi yakınsak kılıp tartışma sebebini ortadan kaldırır. Euler’in kendisi de “\, toplam” kelimesine daha geniş bir anlam vermek gerektiğini söylüyor.
Euler, fikrini daha da ileriye götürüp,
$$1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \cdots
\ =
\frac{2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot 17 \cdot 19 \cdot 23 \cdots}{1 \cdot 2 \cdot 4 \cdot 6 \cdot 10 \cdot 12 \cdot 16 \cdot 17 \cdot 18 \cdot 22 \cdots}$$
eşitliğinden, yani,
$$\sum_{n = 1}^{+\infty} \frac{1}{n} = \frac{2}{2 – 1} \cdot \frac{3}{3 – 1} \cdot \frac{5}{5 – 1} \cdots
= \prod_p \frac{p}{p-1}
= \prod_p \frac{1}{1 – \frac{1}{p}}$$
eşitliğinden başka,
$$\frac
{1 – 2^{n-1} + 3^{n-1} – 4^{n-1} + 5^{n-1} – 6^{n-1} + \cdots}
{1 – \frac{1}{2^n} + \frac{1}{3^n} – \frac{1}{4^n} + \frac{1}{5^n} + \frac{1}{6^n} + \cdots }
\
= \frac{-(n-1)! (2^n – 1)}{(2^{n-1} – 1)\pi^n} \cos \frac{n \pi}{2}$$
eşitliğine erişir ki yaklaşık 100 yıl sonra Riemann’ın keşfedeceği zeta fonksiyonunun (daha doğrusu $\eta(s) = (1 – 2^{1 – s})\zeta(s)$ fonksiyonunun) fonksiyonel denkleminin özel halleridir.
Böylece Euler’in $\prod_p \frac{1}{1 – \frac{1}{p^s}} = \sum_n \frac{1}{n^s}$ özdeşliğiyle Aritmetiğin Temel Teoremi’ni analitik olarak ifade ettiğini ve ($s > 1$ için) $s \mapsto \sum_n \frac{1}{n^s}$ şeklinde tanımlanan zeta fonksiyonunu –adını koymaksızın– incelediğini ve fonksiyonel denklemini matematiğe kattığını görüyoruz. Asal sayılarla ilgili çalışmalarda yeni bir çağ açmıştır.
İki ayrı ispat
Biri kolay biri daha zor iki ispat gördük. Biri Öklid’in verdiği son derece temel kavramlara dayanan ispat, biri Euler’in verdiği zeta fonksiyonuna dayanan diğer ispat.
Euler’in ispatı her ne kadar Öklid’inkinden daha ileri düzeydeyse de, daha çok meyve veren ispattır, çünkü asal sayıları incelemek için kullanılan zeta fonksiyonuna dayanmaktadır. Zeta fonksiyonu asal sayılarla ilgili pek çok sırrı kendi içinde barındırmaktadır. Yeter ki biz o sırları okuyabilecek ve çözebilecek şifrelere sahip olalım. Euler, asal sayılarla zeta fonksiyonu arasındaki ilişkiyi ilk gören kişi olma şerefini taşır.
Herhangi bir pozitif $x \in \mathbb{R}$ sayısı için, $x$’ten büyük olmayan asal sayıların adedini $\pi(x)$ ile gösterelim. Örneğin sayarak $\pi(10) = |{2, 3, 5, 7}| = 4$ ve benzer şekilde $\pi(100) = 25$ olduğunu bulabiliriz. Böylece $\pi : \mathbb{R}^{> 0} \rightarrow \mathbb{R}$ diye bir fonksiyon tanımladık. Asal sayıların sonsuz miktarda olduğunu $\lim_{x \to } \pi(x) = +\infty$ şeklinde ifade edebiliriz.
Şimdi $\pi$ fonksiyonunun grafiğine bakalım. Bir merdiven fonksiyonu olan $\pi$’nin $[0, 200]$ aralığındaki grafiğini aşağıda görebilirsiniz.
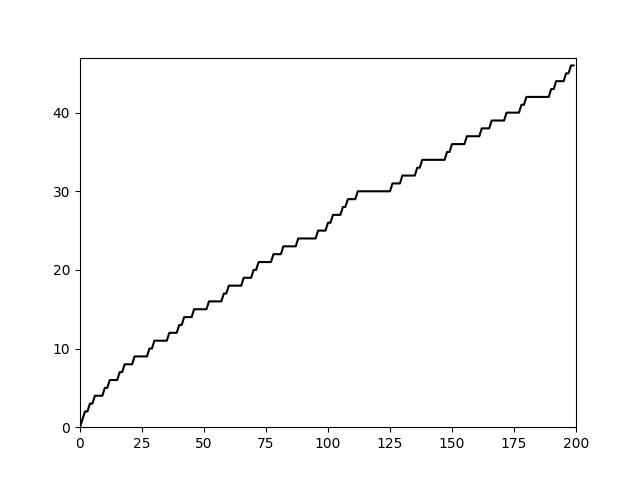
Devamlı olarak artan, fakat ne zaman artacağı pek belli olmayan bir fonksiyon. Son derece kaprisli diyebileceğimiz bu grafik bazen yatay gitmekte bazen arka arkaya yükselmekte ve ne zaman uzun bir yatay çizgi olarak gideceğini, ne zaman yükseleceğini kestiremeyeceğimiz bir davranış sergilemektedir. Bu $\pi$ fonksiyonunun grafiği mesela aşağıdaki grafikten ne kadar da farklı! Aşağıdaki grafik, hiçbir kaprisi olmayan, gayet düzgün, gayet öngörülebilir bir davranış sergilemektedir. “Eğer $\pi$ fonksiyonunun grafiği de buna benzeseydi, belki $\pi$ fonksiyonunu incelemek daha kolay olurdu” diye düşünme eğiliminde olabiliriz.
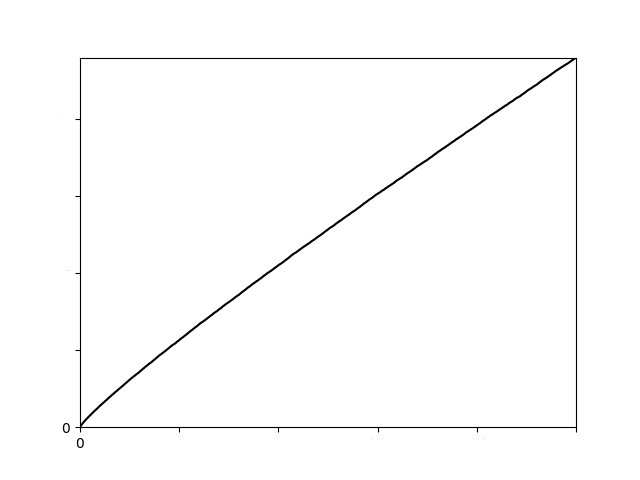
Ancak bu eğilime kapılmayalım. Yukarıdaki grafik de $\pi$ fonksiyonunun grafiğidir! Evet, $[0, 100000]$ aralığındaki grafiği.
İşte asal sayıların dağılımında karşılaştığımız esrarengiz durum budur: bir yanda yakından baktığımızda son derece karışık olan, diğer yandan uzaktan baktığımızda son derece düzgün olan bir fonksiyon. Asal sayıların dağılımının çekiciliği ve esrarı biraz da burada yatmaktadır.
Asal sayı teoremi
İnce davranışına bakınca $\pi$ fonksiyonu çok düzensizdir. Onu basit ve tanıdık fonksiyonlar aracılığıyla ifade etmek mümkün değildir. Matematikçiler bu yüzden $\pi(x)$’e yaklaşık” değerler veren bilindik fonksiyonlar arayışına girdi. Buradayaklaşık” kelimesine açıklık vermek için, $\lim_{x \to +\infty} \frac{\pi(x)}{f(x)} = 1$
bağıntısını sağlayan $f$ fonksiyonlarını kastettiğimizi söyleyelim. Böyle bir $f$ fonksiyonu için “$\pi(x)$, $f(x)$ e asimptotiktir” denir ve $\pi(x) \sim f(x)$ yazılır.
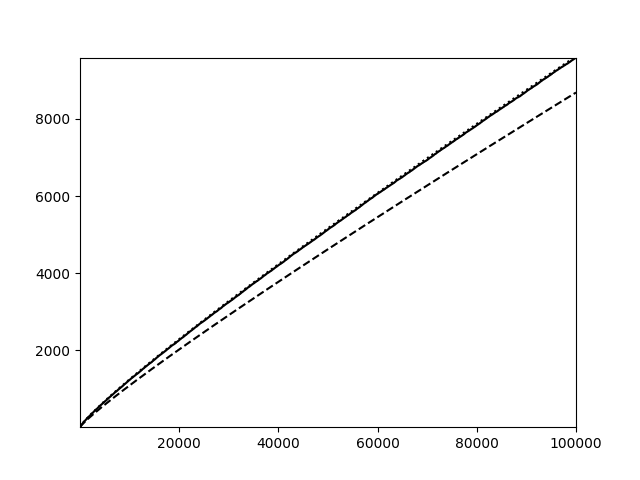
Carl Friedrich Gauss (1777–1855), 1849’da astronom Johann Franz Encke’ye (1791–1865) yazdığı bir mektupta, 1792–93 yıllarında asal sayıların sıklığıyla ilgilendiğini, sıklık tabloları yaptığını, ve bütün salınımına ve düzensizliğe rağmen asal sayıların miktarının ortalamada logaritmayla ters orantılı olduğunu farkettiğini yazar. Yani $\frac{\pi(x)}{x}$ ile $\frac{1}{\log x}$ orantılıdır. Başka türlü söyleyelim: $x$ sınırsız büyüdükçe $\lim_{x \to +\infty} \dfrac{\frac{\pi(x)}{x}}{\frac{1}{\log x}}$ bir sayıya yaklaşır ve asal sayı cetvellerinden görüldüğü gibi bu sayı $1$’dir.
Gauss’un fark ettiği ama ispatlamadığı
$$\lim_{x \to +\infty} \frac{\pi(x)}{\frac{x}{\log x}} = 1$$
eşitliği, tarihe “asal sayı teoremi” diye geçti. Tabii $\frac{x}{\log x}$ yerine $f(x) \sim \frac{x}{\log x}$ şartını sağlayan bir $f$ fonksiyonu da alınabilir. Gauss $Li(x) = \int_2^x \frac{1}{\log t} \, dt$ fonksiyonunu kullanır.
Asal sayı teoremi, $n$’inci asal sayının büyüklüğü hakkında malumat verir. Eğer asal sayı teoremi doğruysa,
$$\lim_{x \to +\infty} \frac{\pi(x) \log x} {x} = 1$$
$$\lim_{x \to +\infty} \log \pi(x) + \log \log x – \log x = 0$$
$$\lim_{x \to +\infty} \log x \bigg( \frac{\log \pi(x)}{\log x} + \frac{\log \log x}{\log x} – 1 \bigg) = 0$$
$$\lim_{x \to +\infty} \bigg( \frac{\log \pi(x)}{\log x} + \frac{\log \log x}{\log x} – 1 \bigg) = 0$$
$$\lim_{x \to +\infty} \frac{\log \pi(x)}{\log x} = 1$$
$$\lim_{x \to +\infty} \frac{\log \pi(x)}{\log x} \frac{\pi(x) \log x} {x} = 1$$
$$\lim_{x \to +\infty} \frac{\pi(x) \log \pi(x)}{x} = 1$$
ve $x$ olarak $n$’inci asal sayı $p_n$’yi seçersek
$\lim_{n \to +\infty} \frac{n \log n}{p_n} = 1$
çıkar, yani $p_n \sim n \log n$’dir.
Tersine $p_n \sim n \log n$ bağıntısından asal sayı teoremi elde edilebilir. Şimdi $\lim_{n \to +\infty}\frac{p_n}{n \log n} = 1$’in doğru olduğunu kabul edelim. Logaritma alarak,
$$\log p_n – \log n – \log \log n \to 0$$
$$\frac{\log p_n}{\log n} – 1 – \frac{\log \log n}{\log n} \to 0$$
$$\frac{\log p_n}{\log n} \to 1, \tag{1}$$
$$\frac{\log p_{n+1}}{\log n} = \frac{\log p_{n+1}}{\log (n+1)} \cdot \frac{\log (n+1)}{\log n} \to 1 \tag{2}$$
elde edilir. Herhangi bir $x > 2$ için $n = \pi(x)$ yazarsak,
$$p_n \leq x < p_{n+1}$$
$$\frac{p_n}{n} \leq \frac{x}{\pi(x)} < \frac{p_{n+1}}{n}$$
$$\frac{\log n}{\log p_{n+1}} \cdot \frac{p_n}{n \log n}
\leq \frac{x}{\pi(x) \log x}$$
$$ < \frac{p_{n+1}}{(n + 1) \log (n + 1)}
\cdot
\frac{n+1}{n}
\cdot
\frac{\log(n+1)}{\log n}
\cdot
\frac{\log n}{\log p_n}$$
bulur, $x$ sınırsız artarken limit alarak,
$$\lim_{x \to +\infty }\frac{x}{\pi(x) \log x} = 1$$
eşitliğinin ispatını tamamlarız.
Böylece $\pi(x) \sim \frac{x}{\log x}$ ile $p_n \sim n \log n$’nin birbirine denk olduğunu öğrendik.
Asal sayı teoreminin aşağıda göreceğimiz ilerletilmelerinden,
$$p_n \leq n \log n + n(\log \log n – 0.9385\dots)$$
gibi sonuçlar da elde edilebilir.
Legendre
Adrien-Marie Legendre (1752–1833), $$\pi(x) = \frac{x}{\log(x) – A(x)}$$
eşitliğiyle tanımlanan $A$ fonksiyonu için $\lim_{x \to +\infty} A(x) = 1,08366\dots$ olduğunu iddia etti. Eğer bu iddiayı ispatlayabilseydi asal sayı teoremini de ispatlamış olurdu. Ancak iddiasını ispat etmekten uzak olduğunun kendisi de farkındaydı.
Legendre’ın, asal sayıların dağılımıyla ilgili bir çalışması da aritmetik dizilerdeki asal sayıların da sonsuzluğu konusundadır. Aralarında asal iki pozitif tamsayı alalım, $a$ ve $b$. Legendre 1808’de $ak + b$ şeklinde sonsuz adet asal sayı olduğunu iddia etti. 1830’da iddiasını daha hassaslaştırarak, $x$’ten küçük böyle asal sayıların adedine $\pi_b(x)$ denilirse, $a$ ile aralarında asal herhangi $b$, $b’$ sayıları için
$\lim_{x \to +\infty} \frac{\pi_b(x)}{\pi_{b’}(x)} = 1$
olduğunu ileri sürdü. Bu iddia, asal sayıların, modülo $a$ kalan sınıflarına eşit dağıtıldığı anlamına gelir. Ancak Legendre’ın verdiği ispat hatalıdır.
Legendre’ın ilk iddiası, $\lim_{x \to +\infty} \pi_b(x) = +\infty$ olduğu, Dirichlet tarafından ispatlanmıştır.
Dirichlet
Adı Fransız ismine benzeyen Alman matematikçi Lejeune Dirichet (1805–1859), Fourier serileri üzerine araştırmalar yapmış ve bir fonksiyonun Fourier serisinin hangi hipotezler altında o fonksiyona yakınsadığına sağlam bir cevap veren ilk kişi olmuştur (1829).
Dirichlet, 1837 yılında çok önemli bir makale sundu. Bu makalede, ilk terimi ve farkı, aralarında asal tamsayılar olan bir aritmetik dizide sonlu sayıda asal sayı bulunduğunun ispatını verdi. İspatı Euler’in fikrine dayanmaktadır. Dizimiz, $a$ ile $b$ aralarında asal ve $k$ pozitif tamsayı olmak üzere, $ak + b$ şeklindeki sayılardan oluşmaktadır. Euler’in $\sum_{p} \frac{1}{p}$ toplamının ıraksadığını elde etmesi gibi, Dirichlet de $\sum_{p \equiv b \pmod a} \frac{1}{p}$ toplamının ıraksak olduğunu göstermeye çalıştı. Başka şekilde söylersek,
$$ \delta_b(m) = \begin{cases}
1 & \textrm{eğer $m \equiv b \pmod a$ ise,} \\
0 & \textrm{eğer $m \not\equiv b \pmod a$ ise}
\end{cases}$$
formülüyle tanımlanan $\delta_b$ fonksiyonunu kullanarak, $\sum_{p} \frac{ \delta_b(p)}{p}$ toplamının ıraksadığını göstermeye çalıştı.
Dirichlet’in muazzam fikri şudur: $ \delta_b$, periyotu $a$ olan periyodik bir fonksiyondur, o halde $ \delta_b$’yi, üzerinde çalışmanın daha kolay olduğu başka periyodik fonksiyonlar cinsinden yazalım. O dönemde adı konmamış olsa da Dirichlet’in yaptığı, $\delta_b$’yi bir Fourier toplamı olarak yazmak ve sonlu gruplarda Fourier analizi yapmaktır.
Böylece $a$ ile aralarında asal olan her $b$ tamsayısı için $\delta_b$ fonksiyonu ele alınabilir. Bunu sağlayan $\varphi(a)$ kadar fonksiyon vardır, $a$ ile aralarında asal olan tamsayılar kümesinde tanımlanmış $a$ periyotlu her fonksiyon bu delta fonksiyonlarının uygun sayılarla çarpımlarının toplamı olarak gösterilebilir. Daha teknik bir dille ifade edersek, ${\delta_b : 0 \leq b < a, (a, b) = 1}$ fonksiyon ailesi, yukarıdaki $a$ periyotlu fonksiyonlar uzayının bir tabanıdır. Dirichlet, daha doğal bir taban keşfetti. Bunlar bugün Dirichlet karakterleri” adını verdiğimiz, periyotu $a$ olan ve (başka şartların yanı sıra) her $m$, $n$ tamsayısı için $\chi(mn) = \chi(m) \chi(n)$ çarpım özelliği olan $\chi$ fonksiyonlarıdır. Böyle Dirichlet karakterlerinin sayısı $\varphi(a)$’dır. Bunlardan birisi: $m$ eğer $a$ ile aralarında asalsa $\chi_0(m) = 1$, asal değilse $\chi_0(m) = 0$ şeklinde tanımlanan $\chi_0$ fonksiyonudur veesas karakter” adını taşır. Karakterlerin “dikgenlik” denilen şu özellikleri vardır:
$$\frac{1}{\varphi(a)}\sum_\chi \chi (b) = \delta_1(b).$$
Dirichlet, her bir $\chi$ karakteri için zeta fonksiyonuna benzeyen ve
$$L(\chi, s) = \prod_p \frac{1}{1 – \frac{\chi(p)}{p^s}} = \sum_n \frac{\chi(n)}{n^s}$$
formülüyle tanımlanan $L$-fonksiyonlarını matematiğe ithal etti. Bunlardan $L(s, \chi_0) = \prod_p \frac{1}{1 – \frac{\chi_0(p)}{p^s}}
= \prod_{p | a} \frac{1}{1 – \frac{1}{p^s}}
= \prod_{p | a} \big(1 – \frac{1}{p^s}\big) \prod_{p} \frac{1}{1 – \frac{1}{p^s}} = \prod_{p | a} \big(1 – \frac{1}{p^s}\big) \zeta(s)$
zeta fonksiyonuna çok benzer ve $s$ $1$’e giderken sınırsız olarak artar. Diğer karakterler için $L(\chi, s)$ fonksiyonu $s = 1$ noktasında tanımlı ve süreklidir. İspatın can alıcı noktası ve en zor kısmı, $\chi \neq \chi_0$ için $L(\chi, 1) \neq 0$ eşitsizliğini göstermektir.
Dirichlet’in ispatını anlatmaya çalışalım ve $L(\chi, 1) \neq 0$ eşitsizliklerinin ispat edilmiş olduklarını farzedelim. O zaman $s$ $1$’e yaklaşırken $\sum_{\chi \neq \chi_0} \log L(s, \chi)$ sınırlı kalır. Diğer taraftan $\lim_{s \to 1} L(s, \chi_0) = \prod_{p | a} \big(1 – \frac{1}{p^1}\big) \lim_{s \to 1} \zeta(s) = +\infty$’dur. Bu yüzden,
$$
A(s) = \log L(s, \chi_0) + \sum_{\chi \neq \chi_0} \log L(s, \chi)
$$
eşitliğinin limiti $+\infty$’dur. Ama
$$A(s) = \sum_{\chi} \log L(s, \chi)$$
$$ = \sum_{\chi} \log \prod_{p} \bigg(1 – \frac{\chi(p)}{p^s}\bigg)^{-1}$$
$$ = – \sum_{\chi} \sum_{p} \log \bigg(1 – \frac{\chi(p)}{p^s}\bigg)$$
$$ = \sum_{\chi} \sum_{p} \sum_m \frac{\chi(p^m)}{p^{ms}}$$
$$ =\sum_{\chi} \sum_{p} \bigg(\frac{\chi(p)}{p^{s}} + \sum_{m=2} \frac{\chi(p^m)}{p^{ms}} \bigg)$$
$$ = \sum_{\chi} \sum_{p} \frac{\chi(p)}{p^{s}} + B(s)$$
eşitliğiyle tanımlanan $B(s)$ fonksiyonu, kolaylıkla gösterilebilir ki, $s = 1$ civarında sınırlıdır. O halde $A(s) – B(s)$ sınırsızdır.
Şimdi $a$ ile aralarında asal bir $b$ sayısı alalım ve $bb’ \equiv 1 \pmod{a}$ şartını bağlayan $b’$ sayısını seçelim. O zaman $s \to 1$ iken limit alırsak,
$$\chi(b’)[A(s) – B(s)] =$$
$$\chi(b’) \sum_{\chi} \sum_{p} \frac{\chi(p)}{p^{s}}$$
$$ = \sum_{p} \sum_{\chi} \frac{\chi(b’)\chi(p)}{p^{s}}$$
$$ =\sum_{p} \frac{\sum_{\chi}\chi(b’p)}{p^{s}}$$
$$ =\sum_{p} \frac{1}{\varphi(a)} \frac{\delta_1(b’p)}{p^{s}}$$
$$ =\frac{1}{\varphi(a)} \sum_{p \equiv b (\mathrm{mod\,}a) } \frac{1}{p^{s}}$$
sınırsız artar, dolayısıyla $p \equiv b (\mathrm{mod\,}a)$ koşulunu sağlayan $p$ asal sayıları sonlu sayıda olamaz. Hatta limitlerin sırasını değiştirme teoremlerinin en kolayını kullanarak
$\sum_{p \equiv b (\mathrm{mod\,}a) } \frac{1}{p}$ serisinin ıraksadığı görebiliriz.
Böylece Euler’in asal sayıların sonsuzluğu için verdiği ispatı Dirichlet’in bir aritmetik dizideki asal sayılara genelleştirdiğini görüyoruz. Ancak Dirichlet asal sayı teoremi üzerinde çalışmamıştır.
Chebychef
Asal sayı teoreminin ispatına doğru ilk ciddi yaklaşımı Pafnuty Chebychef’in (1821–1894) yaptığını görüyoruz. 1851 ve 1852 yıllarında yayımlanan iki makalesinde Chebychef –asal sayı teoremini ispat etmese de– o zaman için önemli sonuçlar elde etmiştir.
Chebychef’in başarılarından biri, Bertrand sanısını ispat etmiş olmasıdır. Bertrand sanısı, her $n$ tamsayısı için $n$ ile $2n$ arasında en az bir asal sayı olduğu önermesidir.
Önce şunu söyleyelim ki Chebychef $\frac{x}{\log x}$ fonksiyonu yerine $\pi(x)$’e ondan daha iyi yaklaşan $Li(x) = \int_2^x \frac{1}{\log t} \, dt$ fonksiyonuyla çalıştı. Yukarıdaki $\pi(x)$ ve $\frac{x}{\log x}$ fonksiyonlarının grafiklerine tekrar bakınız. Bu grafikte $ Li(x)$’in de (nokta nokta çizilmiş) grafiği vardır, ama $\pi(x)$’e o kadar yakındır ki $\pi(x)$’ten zorlukla ayırt edilmektedir!
Chebychef asal sayılarda $1$ artan $\pi$ fonksiyonu yerine, $p$ asal sayısında $\log p$ kadar artan, ve $p^m$ asal sayı kuvvetlerinde $\log p$ kadar artan fonksiyonlarla, yani
$\vartheta(x) = \sum\limits_{p \leq x} \log p$ ve
$\psi(x) = \sum\limits_{m \in \mathbb{N}, p^m \leq x} \log p$
şeklinde tanımlanan $\vartheta$ ve $\psi$ fonksiyonlarıyla çalıştı.
Bu fonksiyonlar $\pi$’den daha kullanışlı ve –görünüşün aksine– daha doğaldır. $\psi$ fonksiyonu, $1$ den $n$’ye kadar olan tamsayıların en küçük ortak katının logaritmasıdır: $\mathrm{ekok}[1, 2 ,\dots, n] = e^{{\psi (n)}}$.
Chebychef,
$$
\pi(x) \sim \frac{x}{\log x}, \quad
\vartheta(x) \sim x, \quad
\psi(x) \sim x
$$
önermelerinin birbirlerine denk olduğunu gösterdi.
İstenildiği kadar büyük bir $M$ sayısı, istenildiği kadar küçük pozitif bir $\epsilon$ sayısı, istenildiği kadar büyük bir $N$ sayısı verilsin; Chebychef,
$$x > N, \pi(x) > \int_2^x \frac{1}{\log t} \, dt – \epsilon \frac{x}{(\log x)^M}$$
$$y > N, \pi(y) < \int_2^y \frac{1}{\log t} \, dt + \epsilon \frac{y}{(\log y)^M}$$
şartlarını sağlayan $x$ ve $y$ sayılarının bulu-nabileceğini ispat etti. Buradan $\lim_{x \to +\infty} \frac{(\log x)^M}{x} \left(\pi(x) – \int_2^x \frac{1}{\log t} \, dt \right) = 0$ elde edilebilir, yani parantez içindeki fark, çok büyük olamaz. Eğer $M = 1$ alınırsa görürüz ki
$$\lim_{x \to +\infty}\frac{\pi(x)}{\frac{x}{\log x}}$$
ya yoktur, ya da vardır ve $1$’e eşittir. Daha teknik bir dille ifade edersek, $$ \liminf_n \frac{\pi(x)}{\frac{x}{\log x}} \leq 1 \leq \limsup_n \frac{\pi(x)}{\frac{x}{\log x}}$$
denilebilir. (Chebychef’in zamanında $\liminf$ ve $\limsup$ kavramları tanımlanmamıştı.)
Chebychef büyük $x$ sayıları için $0,89 \leq \frac{\pi{x}}{\frac{x}{\log x}} \leq 1,11$ olacağını göstermeyi başardı. Bu eşitsizlikler, Legendre’ın $A$ fonksiyonunun limitinin de $1,08366\dots$ olamayacağı sonucunu verir: $A$’nın limiti ya yoktur, ya da vardır ve $1$’e eşittir. Chebychef’in elde ettiği eşitsizlikler daha sonra başka matematikçiler tarafından çok karışık hesaplarla daha da daraltıldı. Ancak böyle daraltmalarla asal sayı teoremini ispat etmenin mümkün olmadığı da bariz olarak anlaşıldı.
Chebychef’in kullandığı aletlerden birisi $\sum_{n = 1}^{+\infty} \psi(\frac{x}{n}) = \log \lfloor x \rfloor !$ eşitliğidir. Bu bağıntı, Selberg ve Erdős’ün ispatlarının da altında yatar.
Mertens
Chebychef’in yöntemlerini hassaslaştıran ve keskinleştiren matematikçilerin belki de en önemlisi Franz Mertens’dir (1840–1927).
Legendre ve Chebychef, $\sum_{p \leq x} \frac{1}{p} – \log \log (x)$ ifadesinin limiti olduğunu ispat etmek için uğraştılar ama ispatlayamadılar.
Mertens, Chebychef’in yöntemlerini incelterek
$\sum_{p \leq x} \frac{1}{p} = \log \log (x) + M + O\big(\frac{1}{\log x}\big)$
bağıntısını ispat etti. Kullandığı önemli yardımcı teorem
$\sum_{p \leq x} \frac{\log p}{p} = \log (x) + O(1)$
eşitliğidir. Buradaki $M$, Mertens sabiti olarak adlandırılan bir sayıdır ve yaklaşık değeri de $0,26149721\ldots$’dır. (Açıklayalım: $f(x) = g(x) + O(h(x))$ gibi bir ifade, $x$ sınırsız büyürken $\frac{f(x) – g(x)}{h(x)}$’in sınırlı kaldığını göstermektedir. Eğer $\frac{f(x) – g(x)}{h(x)}$’nin limiti varsa ve 0’a eşitse, $f(x) = g(x) + o(h(x))$ yazacağız.)
Mertens aritmetik dizilerdeki asal sayıları da incelemiş ve
$$\sum\limits_{\substack{p \leq x \ p \equiv b (\mathrm{mod} a)} } \frac{1}{p} = \frac{1}{\varphi(a)} \log \log (x) + M’ + O\bigg(\frac{1}{\log x}\bigg)$$
eşitliğini elde etmiştir.
Chebychef’in ve Mertens’in yoluyla asal sayı teoremini yahut $\frac{\pi_b(x)}{\frac{x}{\log x}} \sim \frac{1}{\varphi(a)}$ eşitliğini ispatlamak mümkün değildir. Bunlar için yepyeni yöntemlere, taptaze fikirlere ihtiyaç vardır.
Riemann
Bernhard Riemann (1826–1866) 1859 yılında asal sayıların dağılımına dair sadece 8~sayfalık bir makale yayımladı ve yepyeni yöntemler vücuda getirdi. Makalesi, taptaze fikirlerle doludur ve matematik tarihinin en önemli buluşlarındandır.
Euler’in ve Dirichlet’in yalnızca gerçek sayılar için ele aldığı zeta fonksiyonunu, Riemann cüretkâr bir biçimde karmaşık sayılar için tanımlar. İlk bakışta “zeta fonksiyonunu karmaşık bir değişken için tanımlamanın ne faydası olabilir ki?” diye düşünebilecek zihinler, Riemann’ın makalesinden sonra ufukları açılmış, onun ufkunun genişliği karşısında afallamış olarak Riemann’a hayranlık duymadan edemezler.
Riemann $\Re s > 1$ olan değerler için $\sum_{n = 1}^{+\infty} \frac{1}{n^s}$ ifadesiyle tanımlanan zeta fonksiyonunu, bütün karmaşık düzlem üzerinde tanımlıyor. Ancak o herhangi bir fonksiyonu değişik bölgelerde, değişik formüllerle parçalı purçalı tanımlayanlardan değildi; onun hiç ödün vermeyeceği usül, fonksiyonu tek bir formülle bütün tanım bölgesinde tanımlamak ve onu tekil noktalarındaki davranışıyla anlamaktı. Ve zeta fonksiyonunu,
$$\zeta(s) = \frac{(-s)!}{2\pi i} \int_{+\infty}^{+\infty} \frac{(-x)^s}{e^x – 1} \, \frac{dx}{x}$$
şeklinde tanımladı. Burada $s!$ ile \hbox{$s \mapsto \int_{0}^{+\infty} ! e^{-x} x^s dx$} veya $s \mapsto \lim\limits_{m \to +\infty} \frac{1 \cdot 2 \cdot \cdots \cdot m}{(s + 1)(s + 2) \cdots (s + m) } (m + 1)^s$ şeklinde tanımlanan ve pozitif tamsayılar için $1$, $2$, $6$, $24$, $\dots$ tamsayılarını veren faktoriyel fonksiyonunun $s$ karmaşık sayısındaki değerini gösteriyoruz. İntegral bir yol integralidir, alındığı yol: $x$-ekseni boyunca $+\infty$’dan $0$’a uzanan, başnokta etrafında saatin aksi yönünde bir tur atıp, $x$-ekseni boyunca $+\infty$’a geri dönen yoldur.
Zeta fonksiyonunun $\Re s > 1$ için $\prod_p \big(\frac{1}{1 – \frac{1}{p^s}} \big)$ çarpım şeklinde yazılışı ve çarpanların hiçbirinin $0$’a eşit olmayışı, $\Re s > 1$ bölgesinde $0$ değerini almadığını gösterir.
Aynı bölgede $\sum_n \frac{1}{n^s}$ yazılışı, bu bölgede analitik olduğu sonucunu verir. Fonksiyonel denklemden, $\Re(1 – s) > 1$ yani $ Re s < 0$ bölgesinde de analitiktir. Fakat bu $\Re s < 0$ bölgesinde $\big(\frac{s}{2} – 1\big)!$’in sonsuz olduğu noktalar vardır. Bu noktalarda $\zeta(s) = 0$ olur ve $\big(\frac{s}{2} – 1\big)!$’in sonsuz oluşunu dengeler. Böyle noktalara zeta fonksiyonunun “triviyal kökleri” diyoruz. Bunlar $-2$, $-4$, $-6$, \dots sayılarıdır. Zeta fonksiyonun diğer kökleri varsa, onlar $0 \leq \Re s \leq 1$ şeridindedirler ve bunlar da $\xi$ fonksiyonunun kökleridir.
Bu $\xi$ fonksiyonunun kendisine göre simetrik olduğu $\Re s = \frac{1}{2}$ doğrusuna \emph{kritik doğru}, $- 1 < \Re s < 1$ bölgesine de kritik şerit denir.
Riemann’ın baş döndürücü başarılarından biri, $\pi$ fonksiyonu için apaçık bir formül bulmuş olmasıdır. Şöyle ki $\log(1 – u)$’un açılımını ve zeta fonksiyonunun çarpım ifadesini kullanarak $\Re s > 1$ için, $\log\zeta(s) = \sum_p \sum_n \frac{1}{m}\frac{1}{p^{ms}}$ elde edilir.
Eğer $n$ asal sayı kuvveti değilse $a(n) = 0$,
eğer $n = p^m$ asal sayı kuvvetiyse $a(n) = 1/m$ olarak
tanımlanan $a(n)$ sayılarıyla
$\log\zeta(s) = \sum_{n =1}^{+\infty} \frac{a(n)}{n^s}$ yazılabilir. Riemann $\Pi(x) = \sum_{n \leq x} a(n)$ şeklinde tanımlanan $\Pi(x) = \pi(x) + \pi(x^{1/2}) + \pi(x^{1/3}) + \cdots$ fonksiyonu için, $\log \zeta(s)$’nin ince özelliklerini ve henüz tam olarak ispat edilmemiş olan $\xi(s) = \xi(0) \prod_\rho \big(1 – \frac{s}{\rho}\big)e^{\tfrac{s}{\rho}}$ çarpımını kullanarak,
$$\Pi(x) = Li(x) – \sum_{\rho} Li(x^\rho)$$
$$+ \int_{x}^{+\infty} \frac{dt}{t(t^2 – 1) \log t} + \log \xi(0)$$
eşitliğini elde etti. Böylece asal sayılarla zeta fonksiyonunun kritik şeritteki kökleri arasındaki yakın ilişki apaçık bir şekilde ortaya çıktı. Möbius tersine çevirme yöntemiyle $\pi(x)$ için, $x^{\frac{1}{N+1}} < 2$ olacak kadar büyük bir $N$ ile
$$\pi(x) = \sum_{n=1}^{N} \frac{\mu(n)}{n} Li(x^{1/n}) \sum_{n = 1}^{N} \sum_{\rho} Li(x^{\rho/n}) +$$ daha küçük terimler
bağıntısını elde etti. Burada $Li(x^{\rho/n}) = Li(e^{(\log x)\rho/n})$ terimlerinin altında trigonometrik fonksiyonlar vardır. Yukarıdaki formülde $Li(x^{1/n})$ terimlerinden daha ağır basıp basmadıkları belli değildir. Riemann bu hususun araştırılması gerektiğini söyleyerek makalesine son verir. (Hesaplar $\pi(x) < Li(x)$ eşitsizliğini ima ediyordu ve bu eşitsizliğin $x \leq 10^7$ için doğru olduğu biliniyordu ama 1914 yılında John Edensor Littlewood (1885–1977), $\pi(x) – Li(x)$’in işaretinin sonsuz kere değiştiğini ispat etmiştir. İşaretin değiştiği ilk yerin $1,3971 \times 10^{316}$’dan küçük olduğunu biliyoruz. İşte asal sayılarla çalışırken sayısal delillere hiç güvenilemeyeceğinin kanıtı!)
Riemann asal sayı teoremini ispat etmedi. Onun katkısı, meydana getirdiği yepyeni yöntemlerdir. Zeta fonksiyonunu karmaşık değişkenli fonksiyon olarak görmek, karmaşık köklerini araştırmak, $\pi(x)$ için apaçık formül sunmak, çarpım grubunda Fourier dönüşümleri yapmak \ldots Bunların hepsi baş döndürücü katkılardır. Riemann’dan sonra asal sayıların dağılımı üzerine çalışmak, zeta fonksiyonu üzerine çalışmak demek olmuştur.
Riemann’ın yaptıkları ve buldukları, yalnızca makalesinde yazdıklarından ibaret değil. Onun yayımlanmamış çalışmaları ve çalışmalarının müsveddeleri Göttingen Üniversitesi arşivinde korunmaktadır. Bu müsveddeleri inceleyen ve deşifre eden Carl Ludwig Siegel’den (1896–1981) öğreniyoruz ki Riemann fonksiyonel denklemin üçüncü bir ispatını da bulmuştu, hesaplamaların zorluğunu çok azaltan ve bugün adını taşıyan bağıntıyı keşfetmişti. Kendisi zamanından çok ileride bir matematikçiydi, von Mangoldt’un da dediği gibi, fikirlerini anlayacak ve kullanabilecek kişiler, makalesinin yayınlanmasından ancak 34 yıl sonra ortaya çıkmaya başladı.
von Mangoldt
Riemann’dan sonra onun fikirlerinden yola çıkıp yeni katkılar yapan ilk matematikçiler arasında Hans Carl Friedrich von Mangoldt’u (1854–1925) görüyoruz. von Mangoldt önce Riemann formülünün tam bir ispatını verdi. Bu ispat karmaşık ve uzundur, çünkü Riemann’ın ele aldığı $\log \zeta(s)$ çok karmaşık bir fonksiyondur.
Daha sonraki bir çalışmasında von Mangoldt $\log \zeta(s)$ yerine daha uysal olan $- \frac{\zeta'(s)}{\zeta(s)}$ fonksiyonunu ele aldı. $a(n)$ sayıları ve $\Pi(x) = \sum_{n \leq x} a(n)$ fonksiyonu yerine
$- \frac{\zeta'(s)}{\zeta(s)} = \sum_{n =1}^{+\infty} \frac{\Lambda(n)}{n^s}$ açılımında karşımıza çıkan $\Lambda(n)$ sayılarını ve $\psi(x) = \sum_{n \leq x} \Lambda(n)$ fonksiyonunu kullandı.
Riemann’ın,
$$\Pi(x) = \pi(x) + \pi(x^{1/2}) + \pi(x^{1/3}) + \cdots$$
\
$$= Li(x) – \sum_{\rho} Li(x^\rho) + \int_{x}^{+\infty} \frac{dt}{t(t^2 – 1) \log t} + \log \xi(0)$$
formülü yerine çok daha basit olan,
$$\psi(x) = \vartheta(x) + \vartheta(x^{1/2}) + \vartheta(x^{1/3}) + \cdots$$
$$x – \sum_{\rho} \frac{x^\rho}{\rho} + \sum_n \frac{1}{n}\frac{1}{x^{2n}} – \frac{\zeta'(0)}{\zeta(0)}% \qquad (x > 1)$$
formülünü elde etti. Şimdi Chebychef’in $\psi$ fonksiyonunun niçin $\pi$’den daha doğal ve daha kolay olduğu da anlaşılıyor.
Riemann formülünün ispatında en zor kısım, $\sum_\rho Li(x^{\rho})$’nun yakınsadığını göstermektir. Bu seri mutlak yakınsak değildir; o yüzden $\rho$’ların sıralamasının dikkatle yapılması gerekir. Ayrıca sanal kısmı $T$’den küçük olan köklerin sayısı $N(T)$ için Riemann’ın kısaca bahsettiği,
$$N(T) = \frac{T}{2\pi} \log \frac{T}{2\pi} – \frac{T}{2\pi} + O(\log T)$$
bağıntısına ihtiyaç vardır; von Mangoldt bu bağıntıyı ($O(\log T)$ yerine $O((\log T)^2)$ ile) ispat etmiş ve $\sum_\rho Li(x^{\rho})$ nun yakınsadığının ispatını böylece tamamlamıştır.
von Mangoldt’un 1895 tarihli bu çalışması, Hadamard tarafından 1893’te ispatlanan $\xi(s) = \xi(0) \prod_\rho \big(1 – \frac{s}{\rho}\big)e^{\tfrac{s}{\rho}}$ eşitliğine dayanır.
Hadamard
Jacques Hadamard (1865–1963), Riemann’ın $\xi(s) = \sum_{n = 0}^{+\infty} a_{2n} (s – \frac{1}{2})^{2n}$ serisinde geçen katsayıların hakikaten sıfıra çok çabuk yakınsadığını ispat etmeyi başarmıştır.
Zeta fonksiyonunun kritik şeritteki köklerini $\rho$ ile gösterelim. Riemann $\sum_\rho \frac{1}{|\rho|}$’nun ıraksadığını, $\sum_\rho \frac{1}{|\rho|^2}$’nin yakınsadığını tahmin etmişti. Hadamard bu tahminleri doğrulamayı da başarmıştır.
Karmaşık analizde tamfonksiyonların (entire) cins (genus) teorisini geliştiren Hadamard, teorisini zeta fonksiyonuna uygulayıp yukarıdaki serilerin davranışını kullanarak,
$$\xi(s) = \xi(0) \prod_\rho \bigg(1 – \frac{s}{\rho}\bigg)e^{\tfrac{s}{\rho}}$$
eşitliğini göstermiştir.
Şimdi Hadamard’ın ispatı hakkında biraz daha ayrıntı verelim. Hadamard’ın ispatı üç adımdan oluşur. Birinci adımda Hadamard zeta fonksiyonunun, gerçek kısmı 1’e eşit olan köklerinin var olmadığını gösteriyor. İkinci adımda $\int_{0}^{x} \frac{\psi(t)}{t} \, dt$ için Riemann’ın ve von Mangoldt’un formüllerine benzeyen bir formül buluyor $\int_{0}^{x} \frac{\psi(t)}{t} \, dt \sim \frac{1}{2}x^2$ bağıntısını ispatlıyor. Üçüncü adımda bu bağıntıdan $\psi(x) \sim x$ sonucunu çıkarıyor.
Hadamard’ın ispatı karmaşık değerli fonksiyonlar teorisinde –Hadamard’ın da büyük katkılarıyla– yapılan gelişmelerin ürünüdür.
de la Vallée Poussin
Asal sayı teoremini Hadamard’la hemen hemen aynı zamanda, 1896’da, ama ondan bağımsız olarak ispatlayan bir başka sima, Belçikalı matematikçi Charles-Jean de~la~Vallée Poussin’dir (1866–1962). Oldukça uzun olan makalesi üç ayrı kısımdan oluşmaktadır. Üçüncü kısım ve bunların devamı olan dördüncü ve beşinci kısımlar, kuadratik formlarca yazılabilen asal sayılar üzerinedir ve bunlara bu yazımızda değinemeyeceğiz.
Birinci kısımda de~la~Vallée Poussin, asal sayı teoremini ispatlar. Bu ispat üç adımdan oluşur.
Hadamard gibi o da birinci adımda zeta fonksiyonunun, gerçek kısmı 1’e eşit olan köklerinin var olmadığını gösteriyor. İzlediği yol Hadamard’ınkinden daha zor ve daha uzundur, 19 sayfa tutmuştur. İkinci adımda $\sum_{n \leq y} \frac{\Lambda(n)}{n} – \frac{\psi(y)}{y}$ farkının asimptotik davranışını inceliyor. Üçüncü adımda $\theta(x) \sim x$ sonucunu çıkardı.
De la Vallée Poussin, makalesinin ikinci kısmında aritmetik dizilerdeki asal sayıların dağılımını inceliyor ve $\lim_{x \to +\infty }\frac{\pi_b(x)}{\frac{x}{\log x}} = \frac{1}{\varphi(a)}$ eşitliğini ispatlıyor. Limitin var olduğu bilindiğinde limitin $\frac{1}{\varphi(a)}$’ya eşit olduğunu çıkarmak kolaydır, de~la~Vallée Poussin’in başarısı limitin var olduğunu ispatlamakta yatar. Böylece Legendre’ın $\lim_{x \to +\infty }\frac{\pi_b(x)}{\pi_{b’}(x)} = 1$ tahmini doğrulanmıştır: bu limit vardır, ve $1$’e eşittir.
Asal sayı teoremi ispatlandıktan sonra, $\pi(x) -\frac{x}{\log x}$ veya $\pi(x) – Li(x)$ farklarını anlama ve ölçme problemi gündeme gelecekti. Buna en açık cevabı ilk kez veren kişi, de~la~Vallée Poussin olmuştur.
1899 yılında de~la~Vallée Poussin, $\zeta(1 + ti) \neq 0$ teoreminin kendi ispatının fikrini geliştirerek, zeta fonksiyonunun yalnızca $Re s = 1$ doğrusu üzerinde değil, o doğruyu içeren bir bölgede de $0$’a eşit olamayacağını gösterdi. Öyle $a$ ve $t_0$ sayıları vardır ki $B = {\sigma + ti : \sigma > 1 – \frac{1}{a \log |t|} , |t| > t_0}$ bölgesinde zeta fonksiyonunun kökü bulunmaz.
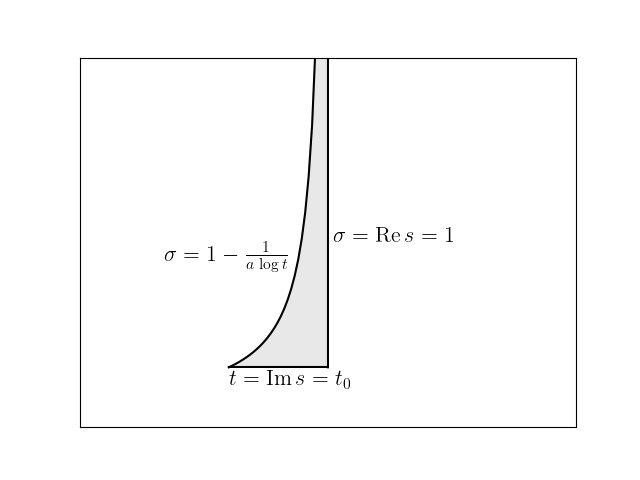
Zeta fonksiyonunun bu bölgede $0$ değerini almaması, $\pi$ ile $x/\log x$ veya $ Li(x)$ arasındaki fark hakkında da bilgi veriyor. de~la~Vallée Poussin, bu bölgenin sıfırsız olmasından, uygun bir $c$ sabitiyle $\psi(x) = x + O(x e^{-c \sqrt{\,\log x}})$ olduğunu ispat etti.
Bu sonucun iki yankısını görelim. İlk olarak, Legendre’ın
$\pi(x) \sim \frac{x}{\log x – A}$ yakınlaştırmasındaki hata terimini, de~la~Vallée Poussin’in sonucuyla birleştirirsek, en iyi hata teriminin $A = 1$ olduğu zaman elde edildiği görülür. İkincisi, $n$ ne olursa olsun,
$\pi(x) \sim \frac{x}{\log x} + \frac{x}{(\log x)^2} \cdots + (n-1)!\frac{x}{(\log x)^n}$
yaklaşımı, $\pi(x) \sim Li(x)$’ten daha az bir hata veremez. Böylece $ Li(x)$’in gerçekten $\frac{x}{\log x}$’ten daha uygun olduğu anlaşılıyor.
Asal sayılar ve kökler
Gerek Hadamard’ın gerek de~la~Vallée Poussin’in ispatlarında, zeta fonksiyonunun $\Re s = 1$ doğrusu üzerinde kökünün olmaması, can alıcı bir rol oynamıştır, böyle bir rol oynaması kaçınılmazdır.
Niçin kaçınılmaz olduğu üzerinde biraz duralım. Asal sayı teoremiyle zeta fonksiyonunun kökleri arasındaki yakın ilişkiyi –yalnızca sezgisel de olsa– açık bir şekilde meydana çıkaran bir akıl yürütmeyi takip etmek faydalı olacaktır. Bu amaçla von~Mangoldt’un,
$$\psi(x) = x – \sum_{\rho} \frac{x^\rho}{\rho} + \sum_n \frac{1}{n}\frac{1}{x^{2n}} – \frac{\zeta'(0)}{\zeta(0)}$$
formülünden hemen,
$$\frac{\psi(x)}{x} \sim 1 + \sum_{\rho}\frac{x^{\rho-1}}{\rho}$$
elde edelim. O halde asal sayı teoremi $\lim_{x \to +\infty} \sum_{\rho}\frac{x^{\rho-1}}{\rho} = 0$ eşitliğine denktir ve eğer terim terim limit almak geçerliyse –ki bu adım hiç mi hiç bariz değildir– her $\rho$ için $x^{\rho-1}$’in, yani $|x^{\rho-1}| = x^{\Re(\rho-1)}$’in limitinin $0$ olmasına, yani her $\rho$ için $\Re \rho < 1$ eşitsizliğine denk olur. Asal sayı teoreminin ispatlarında, $\Re s = 1$ doğrusun üzerinde zeta fonksiyonunun hiç kökünün bulunmadığı önermesinin niçin gerektiğini sezebiliyoruz.
Asal sayı teoremiyle “$\Re s > 0 \text{ ve } \zeta(s) = 0 \implies \Re s \neq 1$” önermesi denk gibidir. Gerçekten de Albert Edward Ingham (1900–1967) asal sayı teoremi doğruysa zeta fonksiyonunun $\Re s = 1$ doğrusu üzerinde kökünün olamayacağını ispat etmiştir.
Tekrar von Mangoldt formülüne dönelim ve geçerli olup olmadığına bakmaksızın her iki tarafın türevini alıp $x$ olarak pozitif bir $n$ sayısı seçelim.
$$\Lambda(n) \sim 1 – \sum_\rho n^{\rho-1}$$ olacaktır;
$$\Re \rho = \sigma$ ve $\Im \rho = \gamma$$ yazarsak,
$$\Lambda(n) \sim 1 – \sum_\rho \frac{1}{n^{1-\sigma}} (\cos(\gamma \log n) + i\sin(\gamma \log n))$$
bulunur. Bu ne demektir? $\Lambda(n)$’ye her bir kökün katkısı vardır; bu katkı: genliği $\frac{1}{n^{1-\sigma}}$ olan bir salınımdır. Salınımın “frekansı” ise $\gamma$ tarafından belirlenir ve $\gamma \log n$ kadardır. Bu yoruma “asal sayıların müziği” deniliyor.
Asal sayıların dağılımı ve sıfırsız bölgeler
Asal sayıların sonsuzluğu yani $\lim_{x \to +\infty} \pi(x) = 0$ eşitliği için Euler’in verdiği ispatın özü (karmaşık analizde anlamlı olan) $\zeta(1) = \infty$ eşitliğidir. Zeta fonksiyonunun $s = 1$ noktasında $0$ olmaktan bir hayli uzak oluşu, sonsuz sayıda asal sayı olduğu sonucunu verir.
Gördük ki zeta fonksiyonunun $\mathrm{Re\,} s = 1$ doğrusunda $0$ değerini almayışı, $\lim_{x \to +\infty} \dfrac{\pi(x)}{\frac{x}{\log x}} = 1$ sonucunu, yani asal sayı teoremini veriyor.
Zeta fonksiyonunun $B = {\sigma + ti : \sigma > 1 – \frac{1}{a \log |t|} , |t| > t_0}$ bölgesinde $0$ değerini almayışından, de la Vallée Poussin
$\psi(x) = x + O(x e^{-c \sqrt{\,\log x}})$
asimptotik bağıntısını elde etmişti.
Benzer şekilde zeta fonksiyonunun $B$’den daha büyük \mbox{$C = {\sigma + ti : \sigma > 1 – \frac{\log \log |t|}{a_1 \log |t|} , |t| > t_1}$} bölgesinde $0$ değerini almayışı, de~la~Vallée Poussin’inkinden daha hassas olan
$\psi(x) = x + O(x e^{-c_1 \sqrt{\,\log x \log \log x}})$
sonucunu verir.
Bu sonuçlar genelleştirilebilir. Ingham, zeta fonksiyonunun sıfırı bulunmayan (uygun tipte) büyük bir bölgensiin bilinmesi durumunda, asal sayı teoremindeki hata teriminin küçültülebileceğini gösterdi. Pál Turán da (1910–1976) bunun tersini ispatladı: hata terimini bilirsek, zeta fonksiyonunun sıfırının bulunmadığı bir bölge bulabiliriz. Böylece hata terimini mümkün olan en küçük hale getirebilmek için zeta fonksiyonunun sıfırsız olduğu en büyük bölgeyi bulma problemine yöneliyoruz.
Riemann sanısı
Fonksiyonel denklem, kritik şeritte zeta fonksiyonunun $(\frac{1}{2} + x) + yi$ gibi bir kökü olması halinde, $(\frac{1}{2} – x) – yi$ sayısının da kökü olması gerektiğini söyler. Yani kritik şerit içinde ve kritik $\Re s = \frac{1}{2}$ doğrusunun sağında bir kök varsa, solunda da bir kök vardır. Bu yüzden $- 1 < \Re s < 1$ şeridinde zeta fonksiyonunun sıfırsız olabileceği en büyük bölge, $\frac{1}{2} <\Re s < 1$ şeridiyle onun simetriği olan $0 <\Re s < \frac{1}{2}$ şerididir. Olabilecek en büyük sıfırsız bölgenin hakikaten sıfırsız olması demek, bütün köklerin gerçek kısmının $\frac{1}{2}$’ye eşit olması, yani bütün köklerin $\Re s = \frac{1}{2}$ doğrusu üzerinde yer alması demektir.
Kritik doğru dışında zeta fonksiyonunun (aşikâr olmayan) kökünün olmadığı önermesi, “Riemann sanısı” olarak bilinir ve ispatı hâlâ bulunamamıştır. Bu, matematiğin en önemli problemlerinden birisidir.
Riemann sanısının doğru olması halinde, hata terimi mümkün olan en küçük halini bulur. Şöyle de diyebiliriz: Riemann sanısı, asal sayıların mümkün olduğu kadar düzenli dağıldığını söyler. Riemann sanısı, $\pi(x) = Li(x) + O(\sqrt{x}\log x)$ veya $\psi(x) = x + O(\sqrt{x} (\log x)^2)$ önermelerine denktir.
Riemann sanısının önemi yalnızca hata terimini küçük kılmasında yatmaz. Onu önemli yapan ve matematikçilerin üzerinde çalışmasına sebep olan pek çok neden vardır ama bunlar konumuzun dışında olduğu için değinmiyoruz. Yalnız şunu ekleyelim: popüler yazılarda rastlanan “Riemann sanısı ispatlanırsa RSA şifreleme sisteminin güvenliği tehlikeye girecektir” gibi ifadeler yanlıştır ve öğretici değil aldatıcıdır.
Riemann sanısının doğruluğuna dair ilk önemli delil, Godfrey Harold Hardy’nin (1877-1947) 1914 yılında, kritik doğru üzerindeki köklerin sonsuz sayıda olduğunu ispatlamasıyla bulundu. Atle Selberg (1917–2007) bu sonucu daha da iyileştirdi ve kritik doğru üzerindeki köklerin sayısının, bütün köklerin sayısına oranının pozitif olduğunu gösterdi. Bu oranın en az $2/5$ olduğunu da John Brian Conrey sayesinde (1955–\;) biliyoruz. \cite{conrey1989} Bilgisayarla yapılan hesaplamalarla da ilk 1,2 trilyon kökün kritik doğru üzerinde bulunduğu anlaşılmıştır.
Ancak sayısal delillere hiç güvenilemeyeceğini de görmüştük. Bunlardan çok daha ikna edici delil, George Pólya’nın (1887–1985) bir fikrinin Andrew Odlyzko’nun (1949–) geniş ve derin araştırmalarında doğru gibi gözükmesidir. Pólya, Edmund Landau’nun (1877-1938) sorusu üzerine, köklerin bir Hermit operatörünün öz değerleri olduğunu göstererek Riemann- sanısının ispat edilebileceği fikrini ortaya atmıştı.Odlyzko’nun hesapları, köklerin bir rasgele Hermit matrisinin öz değerleri gibi davrandığı sonucunu vermektedir.
İspatların yapıları ve Tauber tipi teoremler
Asal sayı teoreminin ilk ispatları karmaşık analizin ileri bahislerine, zeta fonksiyonunun derin teorisine dayanıyordu. Zaman içinde daha az önbilgi gerektiren ispatlar bulundu; bunlar sadeleştirildi, basitleştirildi, daha az teknik hale getirildi.
Bu çalışmalar Tauber tipi teoremlerin bulunmasına ve geliştirilmesine yol açmıştır. Tauber tipi teoremler, ağırlıklı bir ortalama hakkında bilinenlerden başka ağırlıklarla kurulan ortalama hakkında bilgi üreten önermelerdir. Asal sayı teoremi bağlamında kullanılan Tauber tipi teoremler, bir $A$ fonksiyonu için, “eğer $T(x) = \sum_{n = 1}^{\lfloor x \rfloor} A(x/n)$ hakkında birşeyler biliyorsak, bildiklerimizden $A$ hakkında bir bilgi elde edebilir miyiz?” gibi sorulara cevap ararlar. Örneğin, $\int_0^x\psi(x) \sim \frac{x^2}{2}$’den $\psi(x) \sim x$ elde edilebilir mi? Bu sorunun cevabını verecek olan alet, Tauber tipi bir teoremdir. Tauber tipi teoremler bütün ispatlarda az çok yer alırlar.
İlk ispatların sadeleştirilmesi iki yönlü olmuştur: (1) karmaşık analizden tamfonksiyonların cins teorisini ve zeta fonksiyonunun ince özelliklerini
kullanmamaya çalışmak, (2) hipotezleri kolaylıkla kontrol edilebilecek Tauber tipi teoremleri bulmaya ve uygulamaya çalışmak.
Örneğin, Landau, $a_n$’ler pozitif sayılar olmak üzere, $\Re s > 1$ için $f(s) = \sum_{n x= 1}^{+\infty} \frac{a_n}{n^s}$ şeklinde tanımlanan $f$ fonksiyonu ele alındığında, $g(s) = f(s) – \frac{b}{s – 1}$
eşitliğini sağlayan ve
$\Re(z) > 1$ bölgesinde sürekli olan bir $g$ fonksiyonuyla bir $b$ sayısı varsa ve uygun bir $\kappa$ sayısı için,
$$g(s) = O(|\Im t|^\kappa)$$
sağlanıyorsa, o zaman $\lim_{x \to +\infty} \frac{\sum_{n \leq x} a_n}{x} = b$ olacağını ispat etmiştir.
Hardy ile Littlewood, şartını $g(s) = O(e^{c|\Im s|})$’ye zayıflattılar. Bu çalışmalar asal sayı teoreminin ispatını oldukça kolaylaştırdı.
Ancak ispatı kolaylaştırma konusundaki en önemli ilerleme Shikao Ikehara’dan (1904–1984) geldi. Ikehara, doktora hocası Norbert Wiener’in (1894–1964) çalışmalarından yola çıkarak, $g(s)$ üzerinde gibi herhangi bir büyüme hızı şartına gerek olmadığını gösterdi. Wiener-Ikehara teoremi şudur: her $n \in \mathbb{N}$ için $a_n > 0$ ise, $\Re s > 1$ için $\sum_{n = 1}^{+\infty} \frac{a_n}{n^s}$ yakınsaksa, uygun bir $b$ sayısıyla kurulan $g(z) = \sum_n \frac{a_n}{n^s} – \frac{b}{s – 1}$ fonksiyonu sürekli olacak şekilde $\Re s > 1$ bölgesine uzatılabiliyorsa, o zaman $\lim_{x \to +\infty} \frac{\sum_{n \leq x} a_n}{x} = b$’dir.–
Wiener-Ikehara teoremi $a_n = \Lambda(n)$ ve $g(s) = – \frac{\zeta'(s)}{\zeta(s)}$ alınarak uygulandığında, zeta fonksiyonunun $\Re s = 1$ doğrusu üzerinde kökü bulunmadığından, başka bir şey kullanılmaksızın $\psi(s) \sim x$ bağıntısı elde edilir ki bu da asal sayı teoremine denktir. Böylece asal sayı teoreminin epeyce basit bir ispatı elde edilmiş olur.
Ancak kimi Tauber tipi teoremlerin ispatı asal sayı teoreminin ispatından daha zor teknikler kullanır. Bu yüzden zor Tauber tipi teoremler, asal sayı teoreminin ispatını aslında basitleştirmez.
Genel olarak şöyle diyebiliriz: karmaşık analizin ileri kısımlarını kullanacak olursak, kolay Tauber teoremleri yeterli olur; karmaşık analizden kullanacağımız aletleri temel düzeyde tutmak istersek, bu sefer de zor ve ispatı karışık Tauber teoremlerine ihtiyaç duyulur. Karmaşık analizle Tauber tipi teoremler arasında böyle bir denge vardır.
Selberg ve Erdős
Selberg ve Paul Erdős (1913–1996), 1949 yılında karmaşık analiz kullanmaksızın asal sayı teoremini ispat ettiler. Bu ispatlar matematik dünyasında büyük bir heyecan yaratmıştı. Her ikisinin de ispatı yüksek matematik içermese de, basit veya kolayca anlaşılabilir değildir. Her iki ispat da Chebychef’in kullandığı $\sum_{n = 1}^{+\infty} \psi(\frac{x}{n}) = \log \lfloor x \rfloor !$
özdeşliğine dayanır.
Selberg ve Erdős’ün ispatları, başta zeta fonksiyonunu kullamayan ve Tauber tipi bir teoreme de dayanmayan ispatlarmış gibi algılandılar. Ancak Basil Gordon (1931–2012) 1956 yılında her iki ispatın da aslında tamamen Tauber tipi ispat olduğunu gösterdikten sonra onları daha da sadeleştirdi. Chebychef’in özdeşliğini, “Stirling formülü” adını taşıyan,
$$
\log n! = \bigg(n + \frac{1}{2}\bigg) \log n – n + \log \sqrt{2\pi} + O\bigg(\frac{1}{n}\bigg)
$$
eşitliği ve basit bir Tauber tipi teorem kullanarak asal sayı teoreminin yeni bir ispatını vermiştir. Gordon’un kullandığı Tauber tipi teorem şudur: \textsl{Eğer $A$ artan bir fonksiyonsa ve $\sum_{n \leq x} A(x/n) = x \log x + b x + o(x/\log x)$ ise $A(x) \sim bx$’tir}. Stirling formülü, Gordon’un teoreminin hipotezinin sağlandığını gösteriyor.
Selberg ve Erdős’ün ispatları, şeffaflıktan uzaktır. Yalnızca temel yöntemlerin kullanılması bir bedel olarak ispatın tadını kaçırmış gibidir.
Newman
1980 yılında Donald J. Newman (1930–2007), şeffaf bir ispat yayımladı. İşin özü, Ingham’ın bir Tauber tipi teoreminin yeni ve basit bir ispatını vermekte yatıyor. Bu ispat karmaşık analizi içerir, ama karmaşık analizin temeli olan Cauchy kalıntı (residue) teoreminden daha fazlasını kullanmaz. Newman’ın ispatı gerçekten basittir, bugün üniversitelerde lisans düzeyindeki karmaşık analiz derslerinde gösterilebilir.
Makalemizin konusu hakkında daha ayrıntılı bilgi edinmek isteyenler, numaralı kaynağa bakabilirler.
Kaynaklar
[1] Bak, Joseph ve Newman, Donald J. Complex Analysis (düzeltilmiş ikinci baskı), Springer, New\,York Dordrecht, Heidelberg, Londra, 2017.
[2] Chebychef, P. Sur la fonction qui determine la totalité de nombres premiers inférieurs à une limite donnée, Oeuvres I, 27–48, Saint Petersburg, 1899
[3] Chebychef, P. Memoire sur les nombres premiers, Oeuvres I, 49–70, Saint Petersburg, 1899.
[4] Conrey, J.~B. More than two fifths of the zeros of the Riemann zeta function are on the critical line, Journal für die reine und angewandte Mathematik, 399 (1989) 1–26.
[5] Dirichlet, L. Sur la convergence de séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, Journal für reine und angewandte Mathematik (Crelle) 4 (1829) 157–169. Mathematische Abhandlungen I (üçüncü yeniden baskı), 117–131, Chelsea Publishing company, NewYork, 1969.
[6] Dirichlet, L. Über die Darstellung ganz willkürlicher Functionen durch Sinus- und Cosinusreihen, Repertorium der Physik (1837), 152–174. Mathematische Abhandlungen I (üçüncü yeniden baskı), 133–161, Chelsea Publishing company, New\,York, 1969.
[7] Dirichlet, L. Über den Satz das jede unbegrenzte arithmetische Progression, deren erstes Glied und Differenz keinen gemeinschaftliche Factoren sind, unendliche viele Primzahlen enthalt (Berlin Bilimler Akademisi’nde 27 Haziran 1837’de okunmuştur). Mathematische Abhandlungen I (üçüncü yeniden baskı), 313–342, Chelsea Publishing company, New\,York, 1969.
[8] Edwards, H.~M. Riemann’s zeta function, Academic Press, New York, 1974.
[9] Euler, L. Variae observationes circa series infinitas, Commentarii academiae scientiarum Petropolitanae, 9 (1744) 160–188.
[10] Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques}, Mémoires de l’académie des sciences de Berlin, 17 (1768) 83–106.
[11] Gauss, C. F. Tafel der Frequenz der Primzahlen,Werke II, 435–443, 1872.
[12] Gauss, C. F. Encke’ye mektup, Werke II, 444–447, 1872.
[13] Goldstein, C. J. A history of the prime number theorem, American Mathematical Monthly, 80 (1973) 599–615.
[14] Hadamard, J. Essai sur l’étude des fonctions données per leur devéloppement de Taylor, Journal de Mathématiques pures et appliquées, 8 (1892) 101–186.
[15] Hadamard, J. Études sur les propriétés des fonctions entiers et en particulier d’une fonction considérée par Riemann, Journal de Mathématiques pures et appliquées, 9 (1893) 171–215.
[16] Hadamard, J. Sur la distributiones de zéros de la fonction $\zeta(s)$ et ses consequences arithmétiques, Bull. Soc. Math. de France, 24 (1896) 199–220.
[17] Hardy, G. H. Sur les zéros de la fonction $\zeta(s)$ de Riemann, Comptes-rendus, 58 (1914) 1012.
[18] Hardy, G. H. ve Littlewood, J. The Riemann-zeta function and the distribution of primes, Acta mathematica, 41 (1918) 119–196.
[19] Ikehara, S. An extension of Landau’s theorem in the analytical theory of numbers, J. of Math. Phys., 10 (1931) 1–12.
[20] Jaroma, J.H. An Upper Bound on the $n$th Prime, The College Mathematics Journal, 36 (2005) 158–159.
[21] Korevaar, J. A century of complex tauberian theory, Bulletin of the Americal Mathematical Society, 39 (2002) 475–531. % (4)
[22] Landau, E. \textit{Handbuch der Lehre von der Verteilung der Primzahlen} (üçüncü baskı), Chelsea Publishing company, New\,York, 1974.
[23] Landau, E \textit{Zahlentheorie} (üçüncü yeniden baskı), Chelsea Publishing company, New\,York, 1969.
[24] Legendre, A.~M~. Essai sur la théorie de nombres (birinci baskı), 1798, Paris.
[25] Legendre, A.~M~. Essai sur la théorie de nombres (ikinci baskı), 1808, Paris.
[26] Littlewood, J. E. Sur la distribution des nombres premiers, Comptes Rendus, 158 (1914) 1869–1872.
[27] von Mangoldt, H.Zu Riemanns Abhandlung „Über die Anzahl der Primzahlen unter einer gegebenen Grösse“, Journal für reine und angewandte Mathematik (Crelle) 114 (1895) 255–305.
[28] Narkiewicz, W. The Development of Prime Number Theory, Springer, Berlin, Heidelberg, 2010.
[29] Newman, D. J. Simple analytic proof of the prime number theorem, American Mathematical Monthly 87 (1980) 693–696.
[30] Odlyzko, A.~M.Correspondence about the origins of the Hilbert-Polya Conjecture.
[31] Odlyzko, A.~M. The $10^{20}$-th zero of the Riemann zeta function and 175 million of its neighbors, 1989 ve 1992.
[32] Öklid, Öklid’in elemanları (Türkçeye çeviren: Ali Sinan Sertöz), Tübitak popüler bilim kitapları 1011, 2019.
[33] Patterson, S.J. An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics 14, Cambridge University Press, Cambridge, 1988.
[34] Platt, D. ve Trudgian, T. The Riemann hypothesis is true up to $3\cdot 10^{12}$, 2020.
[35] Riemann, B. Über die Anzahl der Primzahlen unter einer gegebenen Grösse, Monatsberichte der Primzahlen unter einer gegebenen Grösse aus dem Jahre 1859, 1860 671–680. Gesammelte Werke I, 145–153, Sandig Reprint Verlag, Lichtenstein, 1978.
[36] Saouter, Y., Trudgian T.S. ve Demichel, P. A still sharper region where $\pi(x) − \li(x)$ is positive, Mathematics of Computation, 84 (2015) 2433–2446.
[37] elberg, A. On the zeros of Riemann’s zeta function, Skr. Norske Vid. Akad., 10 (1942) 1–59.
[38] elberg, A. 1996 Lecture on the History of the Prime Number Theorem.
[39] Siegel, K.~L. Über Riemanns Nachlaß zur analytischen Zahlentheorie, Quellen Studien zur Geschichte der Math. Astron. und Physik B, (1932) 45–80. (Gesammelte Abhandlungen I, 275–310, Springer Verlag, Berlin ve New York, 1966.)
[40] Tao, T. The Riemann zeta function and the prime number theorem.
[41] de la Vallée Poussin, C. Recherches analytiques sur la théorie des nombres premiers. Première partie: La fonction $\zeta(s)$ de Riemann et les nombres premiers en general, Ann. Soc. Sci. Bruxelles 20 (1896) 183–256.
[42] de la Vallée Poussin, C. Recherches analytiques sur la théorie des nombres premiers. Deuxième partie: Les fonctions de Dirichlet et les nombres premiers de la forme linéaire $Mx + N$, Ann. Soc. Sci. Bruxelles 20 (1896) 281–362.
[43] de la Vallée Poussin, C. Sur la fonction $\zeta$ de Riemann et le nombres des nombres premiers inférieurs à une limite donnée, Mémoires couronnés et autres mémoires publiés par l’Académie royale de Belgique, 59 (1899–1890) 1–74.
[44] Wiener, N. Tauberian theorems, Annals of mathematics, 33 (1932) 1–100.
[45] Zagier, D. Die ersten 50 Millionen Primzahlen, Lebendige Zahlen, Mathematische Miniaturen, 39–73, Birkhäuser, Basel, 1981.

