Yıl: 2014-1
Sayı: 98
Lineer cebir konulu bu yazı dizisinde ilkokul öğrencilerine sorulabileceğiniz bir soru ile başlayalım: Sadece koyun ve tavukların bulunduğu bir çiftlik olsun. Çiftlikteki hayvanların kafalarını sayınca $30$, ayaklarını sayınca $80$ buluyorsak çiftlikte kaç koyun, kaç tavuk vardır?
Denklem kurmayı bilmediğimiz yaşlarda bu soruyu nasıl çözdüğümüzü hatırlayalım. Çiftlikteki hayvanların tamamı tavuk olsa, $30$ tavuk için $60$ ayak olması gerekirdi. Bu durumda $80-60=20$ ayak eksik kalıyor. Bu $20$ ayağı tamamlamak için $10$ koyuna ihtiyaç var. Demek ki $80$ ayağın $40$ tanesi $10$ koyuna, $40$ tanesi de $20$ tavuğa aitmiş. Elbette çiftlikteki hayvanların hepsi koyun olsa diye başlayabilirdik.
Bu soruyu Pólya daha eğlenceli şekilde çözüyor: Tavuklara tek ayak üstünde durmalarını, koyunlara da arka ayakları üzerine dikilmelerini söyleyelim ve ayakları tekrar sayalım. Ayak sayısı yarıya ineceğinden $40$ bulacağız. Ayaklarla kafalar arasındaki fark bize koyun sayısının $10$ olduğunu söyler.
Şimdi aynı soruyu denklem kurarak çözelim. Koyun sayısına $K$, tavuk sayısına da $T$ dediğimizde elimizdeki bilgiyi şu şekilde ifade ederiz:
$$\begin{split}
K+T & = 30 \\
4K+2T & = 80.
\end{split}$$
İlk denklemin iki katını ikincisinden çıkartırsak $$2K=20$$
elde ederiz. Yani $10$ tane koyun ve $20$ tane de tavuk vardır.
Bu çözümdeki ilk denklemin iki katını almak, her hayvanın iki ayağı olsa, yani hepsi tavuk olsa demek olarak yorumlanabilir. Bu yoruma göre ilk denklemin iki katını ikincisinden çıkartarak hepsi tavuk olsaydı $20$ ayak eksik kalacaktı ve bu koyun sayısının iki katına eşittir demiş oluyoruz. Öte yandan Pólya’nın çözümündeki adımlar da bize, ikinci denklemi ikiye bölüp, ilk denklemi bundan çıkartarak yukarıdaki denklem sistemini başka bir şekilde çözebileceğimizi söylüyor. Böylece bu denklem sistemini iki farklı şekilde çözmüş olduk.
Yaptığımız işi tekrar düşünelim. Bize bir problem verildi. İlk iş olarak bu probleme karşılık gelen bir denklem sistemi oluşturduk. İkinci olarak da bu denklem sistemini (farklı şekillerde) çözdük. Bu ikisini problemin çözümünün iki ayrı aşaması olarak görebiliriz. Peki, birinci aşamayı tersten yapabilir miyiz? Yani, bize bir denklem sistemi verilse, bu denklem sisteminin karşılık geldiği bir problem bulabilir miyiz? İkinci aşamayla ilgili de şunu soralım: Bize verilen her denklem sisteminin bir çözümü var mıdır, varsa bulabilir miyiz?
Önce ilk soruyu inceleyelim. Bize
$$\begin{split}
K+T &=10\\
6K+8T &=66
\end{split}$$
denklem sistemi verilmiş olsun. Bu denklem sisteminin karşılık geldiği bir problem bulmak istiyoruz. İlk denklemi yine kafa sayısı olarak düşünebiliriz. Fakat ikinci denklemi ayak sayısı olarak görmek için tavuk ve koyunların yerine $6$ ve $8$ ayaklı canlılara ihtiyacımız var. Neyse ki karıncalar ve örümcekler bu ihtiyacımızı karşılıyor. İstersek $T$ yerine $Ö$ yazabiliriz. (Denklem sisteminin sağlanması için $7$ karınca ve $3$ örümcek olmalı.)
Gerekirse $17$ ayaklı uzaylıları, tek gözlü masal karakterlerini kullanarak pek çok denklem sistemine karşılık gelen problemler üretebiliriz. Ama eğer
$$\begin{split}
K+T &=1\\
4K+2T &=3
\end{split}$$
sistemine bakarsak hayal gücümüzü biraz daha zorlamamız gerektiğini görürüz. Çünkü bu denklem sistemini çözdüğümüzde $K=\frac{1}{2}$ ve $T=\frac{1}{2}$ olması gerektiğini buluyoruz. Şimdi şöyle başlayan bir problem yazabiliriz: Sadece tavuk ve koyunların bulunduğu bir çiftlikteki tavukların sayısının yarısıyla koyunların sayısının yarısı $\ldots$ Ama bu problemi kuralları bozmak olarak görenler, hile yaptığımızı iddia edenler olabilir. Böyle tartışmaları önlemek için baştan problemin çözümü olarak ne tür sayıları kullanmaya izin verildiğini söylememiz gerekirdi. Elbette verilen denklem sisteminde hangi sayıların kullanılabileceği ve değişkenleri kendileriyle veya diğer değişkenlerle çarpmaya izin verilip verilmediği de önceden belirtilmeli.
Biz burada değişkenleri kendileriyle veya diğer değişkenlerle çarpmaya izin vermiyoruz. Ancak denklemlerde istediğimiz sayıda değişken kullanmaya izin vereceğiz. Denklemleri yazarken herhangi bir gerçel sayıyı kullanma hakkımız da olacak. Aynı şekilde denklem sistemlerinin çözümlerinin de gerçel sayılar olmasına izin vereceğiz.
Öte yandan gerektiğinde iki sayının toplamı $\ldots$ birincinin üç katıyla ikincinin beş katının toplamı $\ldots$ biçiminde problemler yazabiliriz. Bunun birinci aşamayla ilgili sorumuza cevap verdiğini düşünsek bile burada ikinci aşamayla ilgili yeni bir sorun ortaya çıkıyor. Örneğin, eğer $$ \begin{split} K+T& =1 \\ K+T& =2 \end{split}$$ sistemiyle başlarsak bu sistemin çözümü olacak iki sayının toplamının hem $1$ hem de $2$ olması gerekiyor. Böylece ilk aşamayla ilgili sorunun cevabının da aslında, ikinci aşamayla ilgili sorunun cevabına bağlı olduğunu görüyoruz. Hangi denklem sistemlerinin çözümü vardır? Bir denklem sisteminin çözümü varsa çözümü bulabilir miyiz?
Lineer cebir, bu ilk başladığımız soru gibi soruları çözmek için yukarıda attığımız adımları sistematik bir hale getirme çabası olarak doğmuştur. Tabii ki matematiğin her dalı gibi çalışıldıkça dallanıp budaklanmış, matematiğin standart araçlarından biri haline gelmiştir. Aşağıda öncelikle “ilk başladığımız gibi sorular” ile ne kastettiğimizi netleştirip, takip ettiğimiz adımlar nasıl sistematik hale getirilir sorusuna cevap arayacağız.
Şimdiden belirtmekte fayda var: Burada gerçel sayılar kümesiyle çalışacağız; yani katsayılar, çözümler, ileride tanımlayacağımız vektörler ve matrislerin girdileri vs. gerçel sayılar olacak. Matematiksel ifadelerde geçen $x$, $y$, $z$, $w$ gibi alfabenin sonunda yer alan harfler (bazen $x_1$, $x_2$, $x_3$ gibi indislenmiş olarak) değişkenleri gösterecekler. Ayrıca $a$, $b$, $c$, $d$, $\ldots$ gibi alfabenin başlangıç harfleri de (yine bazen $a_1$, $a_2$, $a_3$ gibi indislenmiş olarak) gerçel sayıları gösterecek.
İlk başladığımız soru gibi sorular lineer denklem sistemleriyle ifade edilebilen sorulardır. En basit ifadeyle, lineer denklemler, içinde geçen değişkenlerin sadece kendilerinin gözüktüğü denklemlerdir: mesela $x^2$, $\sin x$ gibi terimler gözükmez. Daha hassas olmak gerekirse, $a_1x_1+…+a_nx_n=d$ şeklindeki birkaç denklemi göz önüne alacağız ve bu denklemleri bir arada sağlamaya çalışacağız. Böyle bir sistemi sağlayan $(s_1,,…,s_n)$ gerçel sayı $n$-lilerine o sistemin bir çözümü diyeceğiz.
En güzeli bir örnek üzerinde çalışmak.
Örnek 1. Şu lineer sisteme bakalım:
$$\begin{split}
7x_3 &=14 \\
4x_1+\frac{1}{2}x_2-x_3 &=7 \\
x_1-x_2+3x_3 &=5.
\end{split}$$
Bu lineer sistemin çözümü olan $(s_1,s_2,s_3)$ üçlülerini bulmak istiyoruz.
İlk olarak 1. ve 3. satırların yerlerini değiştirip şu yeni sistemi elde edelim:
$$\begin{split}
x_1-x_2+3x_3 &=5 \\
4x_1+\frac{1}{2}x_2-x_3 &=7 \\
7x_3 &=14.
\end{split}$$
Şimdi de bu yeni sistemin 3.satırını $\frac{1}{7}$ ile çarpalım:
$$\begin{split}
x_1-x_2+3x_3 &=5 \\
4x_1+\frac{1}{2}x_2-x_3 &=7 \\
x_3 &=2.
\end{split}$$
Son olarak da 1.satırının $-4$ katını 2.satıra ekleyelim:
$$\begin{split}
x_1-x_2+3x_3 &=5 \\
\frac{9}{2}x_2-13x_3 &=-13 \\
x_3 &=2.
\end{split}$$
Bu son denklem sisteminde $x_3=2$ olduğunu biliyoruz; bunu ikinci satırda yerine koyarsak $x_2=\frac{26}{9}$ buluruz ve bunları da ilk satırda yerine koyduğumuzda $x_1=\frac{17}{9}$ çıkar. Yani $(\frac{17}{9},\frac{26}{9},2)$ en son denklem sisteminin bir çözümüdür. Biraz aşağıda aslında bunun ilk başladığımız denklem sisteminin de bir çözümü olduğunu göreceğiz.
Gauss İndirgemesi ve Eşelon Form
Yukarıdaki örnekte yaptığımız iş, çeşitli yasal hamleleri kullanarak, denklem sistemini basamaklı hale getirip daha rahat çözmek şeklinde özetlenebilir.
Verilen bir lineer sisteme uygulanabilecek aşağıdaki işlemleri yasal sayacağız ve bunlara Gauss hamleleri diyeceğiz:
- İki denklemin yerini değiştirmek.
- Bir denklemin her iki kısmını $0$ olmayan bir sayıyla çarpmak.
- Bir denkleme bir başka denklemin bir gerçel sayı katını eklemek.
Bu hamlelerle biri diğerinden elde edilebilen lineer denklem sistemlerine denk sistemler denir. (Bunun bir denklik bağıntısı olduğunu okuyucu kontrol etmeli. Mesela simetri özelliği için bu hamlelerin hepsinin tersinir olduğuna dikkat etmek gerekli.)
Denk lineer sistemlerin çözümlerini düşünelim. Birinci ve ikinci tür hamlelerin çözümleri değiştirmediği oldukça açık. Sadece üçüncü hamle biraz karmaşıkça. Mesela
$$ \begin{array}{cccccc}
a_{11}x_1 &+& a_{12}x_2 &+& \cdots &+& a_{1n}x_n &=& d_1 \\
a_{21}x_1 &+& a_{22}x_2 &+& \cdots &+& a_{2n}x_n &=& d_n \\
\vdots & & \vdots & & \vdots & & &=&\vdots \\
a_{m1}x_1 &+& a_{m2}x_2 &+& \cdots &+& a_{mn}x_n &=& d_m
\end{array} $$
sistemini ve bu sistemin bir $(s_1,…,s_n)$ çözümünü alalım. Sadece bir satırın yapısını değiştirelim: Eğer $i$’inci satıra $j$’inci satırın $k$ katını eklersek elde ettiğimiz yeni $i$’inci satır şöyle olacak:
$$(a_{i1}+ka_{j1})x_1+…+(a_{in}+ka_{jn})x_n=d_i+kd_j \ .$$
Burada $(s_1,…,s_n)$’nin yeni satırın da bir çözümü olduğu yerine yazılarak görülebilir.
Ayrıca yukarıda bahsettiğimiz tersinirlikten dolayı, sadece ilk sistemin çözümlerinin aynı zamanda ikinci sistemin çözümü de olduğunu göstermek yeterli. Bu gözlemleri kullanarak aşağıdaki teoremin ispatını okuyucuya alıştırma olarak bırakıyoruz.
Teorem 1. Denk lineer sistemlerin çözümleri aynıdır.
Lineer denklem sistemlerini çalışırken matris gösterimini kullanmak çok faydalıdır. Bir matris, kısaca dikdörtgen şeklinde yazılan bir dizilimdir. Şimdilik fazla detaya girmeden Örnek 1’i bir matrisle ifade edelim:
$$\left(
\begin{array}{rrr|r}
0& 0& 7& 14 \\
4& \frac{1}{2}& -1& 7 \\
1& -1& 3& 5 \\
\end{array}
\right) \ .$$
Yaptığımız Gauss hamlelerinin matrisle gösterimi de şöyle:
$$\begin{split}
& \left(
\begin{array}{rrr|r}
\, 0& 0& 7& 14 \,\\
4& \frac{1}{2}& -1& 7\, \\
1& -1& 3& 5\, \\
\end{array}
\right) \\
& \\
\underrightarrow{\rho_1\leftrightarrow \rho_3} \; & \left(
\begin{array}{rrr|r}
\, 1& -1& 3& 5\,\\
4& \frac{1}{2}& -1& 7\,\\
0& 0& 7& 14\,
\end{array} \right)\\
&\\
\underrightarrow{\frac{1}{7} \rho_3} \; & \left(
\begin{array}{rrr|r}
\,1& -1& 3& \hphantom{1}5\,\\
4& \frac{1}{2}& -1& 7\,\\
0& 0& 1& 2\,
\end{array} \right) \\
& \\
\underrightarrow{-4\rho_1+\rho_2} \; & \left(
\begin{array}{rrr|r}
\, 1& -1& 3& 5\,\\
0& \frac{9}{2}& -13& -13\,\\
0& 0& 1& 2\,
\end{array}
\right) \ .\end{split}$$
Gauss hamlelerini hangi notasyonla gösterdiğimize dikkat edin.
Matrisleri $A$, $B$, $C$ gibi büyük harflerle göstereceğiz. Bir matrisin $i$’inci satır ve $j$’inci sütundaki girdisi $a_{ij}$ ise o matrisi $(a_{ij})_{i,j}$ şeklinde veya bir karışıklık yaratmadığı durumlarda $(a_{ij})$ şeklinde ifade edeceğiz. Şimdi $m \times n$’lik bir matrisin her satırına bir sayı atayacağız. Matrisin $i$’inci satırına atayacağımız sayıyı $b(i)$ ile göstereceğiz. Eğer $i$’inci satırda $0$ olmayan ilk girdi $a_{ij}$ ise $b(i)=j$ ve eğer $i$’inci satırın tümü $0$ ise $b(i)=n+i$ olarak tanımlayacağız.
Eğer bir $A=(a_{ij})_{i,j}$ matrisinde $i=2,3,…$ için $b(i)>b(i-1)$ ise, $A$ eşelon formdadır diyeceğiz. Bu yukarıda bahsi geçen, bir denklem sisteminin “basamaklı” olmasının formel tanımı.
Örnek 1’e tekrar baktığımızda, sistemin bulduğumuzdan başka çözümü olmadığını görüyoruz. Peki durum her zaman böyle mi? Tabii ki hayır! Öyle olsa işler çok kolay (ve de sıkıcı) olurdu. En azından $0\,x=1$ gibi denklemin hiç çözümü olmadığı açık, ama -aşağıda göreceğimiz gibi- daha karmaşık sistemlerin de çözümsüz olması ihtimali var. Bunlardan başka durum var mı? Evet var! Bazı sistemlerin de sonsuz tane çözümü olabilir. Daha da yok! Yani çözüm kümesi ya boş, ya tek elemanlı ya da sonsuz. Bunu daha sonra kanıtlayacağız, ama ilk önce, bahsettiğimiz son iki duruma birer örnek verelim:
Denklem sistemimiz şu matrisle verilsin:
$$\left(
\begin{array}{rr|r}
1& 3& 1\\
2& 1& -3\\
2& 2& 0
\end{array}
\right)\ .$$
(İlk sütuna denk gelen değişkene $x$, ikincisine denk gelene de $y$ diyelim.)
Burada ilk satırın $-2$ katını ikinci ve üçüncü satırlara eklediğimizde
$$\left(
\begin{array}{rr|r}
1& 3& 1\\
0& -5& -5\\
0& -4& -2
\end{array}
\right)$$
matrisini elde ederiz. Son olarak da ikinci satırın $-\frac{4}{5}$ katını üçüncüye eklediğimizde eşelon formdaki
$$\left(
\begin{array}{rr|r}
1& 3& 1\\
0& -5& -5\\
0& 0& 2
\end{array}
\right)$$
matrisi çıkar. Bu matrisin verdiği sistemi yazalım: $$\begin{split}x+3y&=1 \\ 0x-5y& =-5\\ 0x+0y&=2.\end{split}$$
Bu sistemin en son satırında $x$, $y$ yerine hangi gerçel sayıları koyarsak koyalım $0=2$ elde ederiz. Yani bu son satırın bir çözümü olamayacağından, sistemin de bir çözümü yoktur.
Son olarak da
$$\left(
\begin{array}{rr|r}
1& 3& -2\\
2& 6& -4
\end{array}
\right)$$
matrisine bakalım. (Yine ilk sütuna denk gelen değişken $x$, ikincisine denk gelen $y$ olsun.)
İlk satırın $-2$ katını ikincisine eklediğimizde
$$\left(
\begin{array}{rr|r}
1& 3& -2\\
0& 0& 0
\end{array}
\right)$$
matrisini elde ederiz. Bu durumda da ilgilendiğimiz sistem
$$\begin{split}
x+3y &=-2\\
0x+0y &=0
\end{split}$$
olur. Bu son satırın anlamı nedir? Her şey ve hiçbir şey! Çünkü $x$ ve $y$ yerine konulan her gerçel sayı değeri için $0=0$ eşitliği elde ederiz. Bu da aslında bu son satırın çözüm kümesi hakkında hiçbir bilgi vermemesi demek. Yani başladığımız sistemin çözümleri $s_1+3s_2=-2$ eşitliğini sağlayan $(s_1,s_2)$ ikilileri olur. Buradan $s_1$’in $-3s_2-2$’ye eşit olduğunu görüyoruz. Demek ki başladığımız sistemin çözümleri $s$ bir gerçel sayı olmak üzere, $(-3s-2,s)$ formundaki ikililer. Bunlardan sonsuz tane olduğu açık; çünkü her $s$ gerçel sayısı için bir çözüm var. Burada detayıyla incelemekte fayda olan bir durum var: İkinci değişkenin yerine ne koyduğumuzun bir önemi yok. Bir başka deyişle, verilen her gerçel sayı için ikinci koordinatı o sayı olacak şekilde bir çözüm ikilisi bulabiliyoruz. İleride bu tür değişkenlere serbest diyeceğiz.
Homojen Sistemler
Lineer sistemlerin çözümlerini anlamak için önce sadece belirli bir tipte sistemleri inceleyeceğiz. Sonra bunları kullanarak genel lineer sistemlerin çözüm kümesini kolayca bulacağız. İlk bakacağımız sistemler $a_1 x_1+…+a_n x_n=0$ türünde denklemlerden oluşuyor. Bu sistemlere homojen sistemler denir. Homojen sistemleri temsil eden matrisler
$$\left(
\begin{array}{cccc|c}
a_{11}& a_{12}& \ldots& a_{1n}& 0\, \\
a_{21}& a_{22}& \ldots& a_{2n}& 0\, \\
\vdots& \vdots& \ddots& \vdots& \vdots\,\\
a_{m1}& a_{m2}& \ldots& a_{mn}& 0\,
\end{array}
\right)$$
şeklinde olur. Yani aslında son sütuna gerek yok ve biz bunun yerine
$$\left(
\begin{array}{cccc}
a_{11}& a_{12}& \ldots & a_{1n}\\
a_{21}& a_{22}& \ldots& a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1}& a_{m2}& \ldots & a_{mn}
\end{array}
\right)$$ yazalım.
Her homojen sistemin en az bir çözümü vardır. Bu çözüm $(0,\ldots,0)$, yani sıfır $n$-lisidir. Bunun dışında bir çözüm daha olduğunda, sonsuz tane çözüm olduğunu göstereceğiz. Bunu yapmak için ilk olarak serbest değişken kavramını tanımlayalım:
- Eşelon formdaki homojen bir lineer sistemin matrisle ifadesinde, her satırda $0$ olmayan ilk girdinin tekabül ettiği değişkene, o satırın baş değişkeni diyeceğiz.
- Eşelon formdaki homojen bir lineer sistemde hiçbir satırın baş değişkeni olarak gözükmeyen değişkenlere serbest değişken diyeceğiz.
Bu kavramları örneklerle pekiştirelim.
İlk olarak şu matrisle verilen homojen sisteme bakalım:
$$\left(
\begin{array}{rrr}
1& 0& 3\\
0& 1& -2\\
0& 0& 2
\end{array}
\right) \ .$$
Eşelon formdaki bu sistemde $x$, $y$, $z$ sırasıyla sütunlara tekabül eden değişkenler olsun. Bu durumda $x$ ilk satırın baş değişkeni, $y$ ikincinin, $z$ de üçüncünün. Yani bütün değişkenler baş değişken olarak gözüktüğü için serbest değişken yok. Son satırdan dolayı $z$ yerine sadece $0$ koyabiliyoruz; benzer biçimde üst satırlara çıkarak, öteki değişkenlerin yerine de $0$’dan başka gerçel sayı koyamayacağımızı görürüz. Kısacası yerine serbestçe gerçel sayılar koyabileceğimiz bir değişken yok.
Bir de şu sisteme bakalım:
$$\left(
\begin{array}{rrr}
1& 0& 3\\
0& 1& -2\\
1& 2& -1
\end{array}
\right) \ .$$
Eşelon forma dönüştürmek amacıyla üçüncü satıra ilk satırın $-1$, ikinci satırın da $-2$ katını ekleyelim:
$$\left(
\begin{array}{rrr}
1& 0& 3\\
0& 1& -2\\
0& 0& 0
\end{array}
\right)\ .$$
Şimdi denklem sistemimiz eşelon forma geldi. İlk satırın baş değişkeni $x$, ikincisininki $y$ oldu; ama $z$ hiçbir satırda baş değişken olarak gözükmediği için serbest oldu. Bu koşullarda da $z$’ye keyfi değerler verebiliriz ve bu değerlere göre $x$ ve $y$ değişkenlerine hangi gerçel sayı değerleri verebileceğimize bakarız. Diyelim ki $z$ yerine $s$ gerçel sayı değerini koyduk; o zaman $x$ yerine $-3s$ ve $y$ yerine de $2s$ değerini koymak gerekir. Yani sistemimizin çözümleri $(-3s,2s,s)$ şeklindeki gerçel sayı üçlüleri olur.
Bu örneklerin serbest değişkenlerin varlığının nasıl sonsuz tane çözümü gerektirdiği hakkında ipucu vermiş olması lazım. Bunu daha titizce açıklamak için bir takım yeni kavramlar geliştirmek gerekiyor.
Vektörler ve Vektörler Üzerindeki İşlemler
Yukarıda dikdörtgen biçimindeki dizilimlere matris dediğimizden bahsetmiştik. Bu dikdörtgen $m$ satır ve $n$ sütundan oluşuyorsa bu dizilime $m \times n$’lik bir matris denir. Tek sütunlu matrislere de vektör denir. Aslında vektörler, gerçel sayı $m$-lilerinin yan çevrilmiş hali:
$$\left(
\begin{array}{c}
s_1 \\
s_2 \\
\vdots \\
s_m
\end{array}
\right)\ .$$
Tek satırlı matrislere de satır vektörü denir.
İleride karşımıza çıkacak çeşitli teknik sebeplerden dolayı, lineer denklem sistemlerinin çözümlerini yukarıda yaptığımız gibi satır vektörleriyle değil, vektörlerle göstereceğiz.
Bir $n>0$ doğal sayısı için, $n$ bileşenli vektörlerin kümesini $\mathbb{R}^n$ ile göstereceğiz. Bu küme üzerinde iki temel cebirsel işlem tanımlanır:
$$ \begin{split} & \text{Toplama: } \; \left(
\begin{array}{c}
s_1 \\
s_2 \\
\vdots \\
s_n
\end{array}
\right) +
\left(
\begin{array}{c}
t_1 \\
t_2 \\
\vdots \\
t_n
\end{array}
\right) =
\left(
\begin{array}{c}
s_1+t_1 \\
s_2+t_2 \\
\vdots \\
s_n+t_n
\end{array}
\right) \\ & \\ & \text{Skaler Çarpma: } \; r \left(
\begin{array}{c}
s_1 \\
s_2 \\
\vdots \\
s_n
\end{array}
\right) =
\left(
\begin{array}{c}
rs_1 \\
rs_2 \\
\vdots \\
rs_n
\end{array}
\right) \ . \end{split}$$
Bu işlemlerin şu anda üzerinde çok durmayacağımız, birleşme, değişme, dağılma gibi özellikleri var. Vektörleri her seferinde uzun uzun sayı dizilimleri yerine $\vec{v}$ şeklinde göstereceğiz ve çok gerekmediği sürece de girdi sayısından bahsetmeyeceğiz. Mesela $\vec{v}+ \vec{w}$ vektöründen bahsediyorsak, $\vec{v}$ ve $\vec{w}$ vektörlerin girdi sayılarının aynı olması gerekli.
Şimdi elimizdeki bu yeni kavramlarla, en son örneğe bir daha bakalım. Oradaki sistemin çözümleri
$$\left(
\begin{array}{c}
-3s\\
2s\\
s
\end{array}
\right)$$
şeklindeydi. Skaler çarpımı kullanarak bu vektörü
$$ s \left(
\begin{array}{r}
-3\\
2\\
1
\end{array}
\right)
$$
olarak yazabiliriz. Bu durumda sistemin çözümlerini
$$\vec{v}=
\left(
\begin{array}{r}
-3\\
2\\
1
\end{array}
\right)$$
olmak üzere $s \vec{v}$ şeklinde son derece derli toplu halde ifade edebiliriz.
İçinde birden fazla serbest değişken gözüken homojen bir sisteme bakalım:
$$\left(
\begin{array}{rrrr}
-1& 2& 0& 7\\
0& 1& -3& -2
\end{array}
\right) \ .$$
Değişkenlere $x_1$, $x_2$, $x_3$, $x_4$ diyelim. Bunlardan son ikisi serbest değişkendir. Bunlar sırasıyla $s$ ve $t$ gerçel sayılarını koyalım. İkinci satırdan dolayı $x_2$ yerine $3s+2t$ koymak gerekli. Bu durumda $x_1$ yerine de
$$2(3s+2t)+7t=6s+11t$$
koymak lazım. Yani çözüm kümesinin elemanları
$$\left( \begin{array}{c} 6s+11t \\ 3s+2t \\ s \\ t \end{array}\right)$$ formunda olur. Bu tür vektörleri de
$$s\left(
\begin{array}{c}
6\\
3\\
1\\
0
\end{array}
\right) +
t\left(
\begin{array}{c}
11\\
2\\
0\\
1
\end{array}
\right)$$
şeklinde ifade edebiliriz.
Buradan bir genellemeye varılabilir mi? Yani sistemin $m$ tane serbest değişkeni varken, sistemin çözümü olan sabitlenmiş $\vec{v}_1,\ldots,\vec{v}_m$ vektörleri için her çözüm
$$s_1 \vec{v}_1+\cdots+s_m \vec{v}_m$$
formunda mıdır?
Verilen $\vec{v}_1,\ldots,\vec{v}_m$ vektörleri için $s_1,\ldots,s_m \in \mathbb{R}$ olmak üzere
$$s_1 \vec{v}_1+\cdots +s_m\vec{v}_m$$
formundaki vektörlere $\vec{v}_1, \ldots ,\vec{v}_m$’nin bir lineer kombinasyonu denir ve bu tür vektörlerin kümesi $\left<\vec{v}_1,\ldots,\vec{v}_m\right>$ olarak gösterilir.
Şuna dikkat edelim: Eğer $\vec{v}_1,\ldots,\vec{v}_m$ vektörleri bir homojen sistemin çözümleriyse, bu vektörlerin her lineer kombinasyonu da aynı homojen sistemin çözümüdür.
Teorem 2. Homojen lineer denklem sistemlerinin çözüm kümeleri $\left<\vec{v}_1,\ldots,\vec{v}_m\right>$ formundadır.
Kanıt. İlk olarak, Gauss hamlelerini kullanarak sistemi eşelon formuna getirelim. Bunu yapınca sistemi temsil eden matris şöyle gözükecek:
$$\left(
\begin{array}{ccccc|c}
a_{11}& a_{12}& a_{13}& \ldots& a_{1n}& 0\\
0& a_{22}& a_{23}& \ldots& a_{2n}& 0\\
0& 0& a_{33}& \ldots& a_{3n}& 0\\
\vdots& \vdots& \vdots& \ddots& \vdots & \vdots\\
0& 0& 0& 0& a_{nn}& 0\\
0& 0& 0& 0& 0& 0\\
0& 0& 0& 0& 0& 0
\end{array}
\right) \ .$$
Burada dikkat edilmesi gereken birkaç şey var. Öncelikle $0$ olarak yazmadığımız bazı $a_{ij}$’ler $0$ olabilir. Ayrıca satırların burada göründüğünden daha önce bitme ihtimali var. Yani yukarıda $n.$ satır gözükmeyebilir ya da onun altındaki sadece $0$ olan satırlar gözükmeyebilir. Yani bu matris tam olarak içinde bulunduğumuz durumu ifade etmiyor, ama dikkatli olduğumuz sürece sorun yok.
Eğer $a_{nn}$ gözüküyorsa ve $0$ değilse, $x_n$ yerine sadece $0$ koyabileceğimiz açık. Sonrasında bir üst satıra geçebiliriz ve oradaki $a_{n-1\,n}$’yi yok varsayabiliriz (niçin?) ve baş değişkenini o satırdaki serbest değişkenler cinsinden yazabiliriz. Bu şekilde devam ederek, her satırın baş değişkenini serbest değişkenler cinsinden yazabiliriz.
Diyelim ki
$$i_1<i_2< \cdots<i_k \quad \text{ ve } \quad j_1<j_2<\cdots<j_m$$
olmak üzere $x_{i_1},x_{i_2},\ldots,x_{i_k}$ baş değişkenler, $x_{j_1},x_{j_2},\ldots,x_{j_m}$ de serbest değişkenler olsun. Ayrıca $x_{i_1},x_{i_2},\ldots,x_{i_k}$ değişkenlerinin $x_{j_1},x_{j_2},\ldots,x_{j_m}$ cinsinden ifadeleri şöyle olsun:
$$\begin{split}
x_{i_1}& =b_{i_1,j_1}x_{j_1} &+b_{i_1,j_2}x_{j_2} &+\cdots +b_{i_1,j_m}x_{j_m}\\
x_{i_2}& =b_{i_2,j_1}x_{j_1} &+b_{i_2,j_2}x_{j_2} &+\cdots +b_{i_2,j_m}x_{j_m}\\
& & \vdots \;\; & \\
x_{i_k}& =b_{i_k,j_1}x_{j_1} &+b_{i_k,j_2}x_{j_2} &+\cdots +b_{i_k,j_m}x_{j_m}.
\end{split}$$
Şimdi $s=1,\ldots,m$ için $\vec{v}_s$ vektörü şöyle tanımlanır:
- Eğer $t=i_p$ ise $\vec{v}_s$’in $t.$ koordinatı $b_{i_p, j_s}$ olur.
- Eğer $t=j_s$ ise $\vec{v}_s$’in $t.$ koordinatı $1$ olur.
- Eğer $t=j_p$ $(p\neq s)$ ise $\vec{v}_s$’in $t.$ koordinatı $0$ olur.
Bu vektörlerin her birinin sistemimizin bir çözümü ve her çözümünün de $\left<\vec{v}_1,\ldots,\vec{v}_m\right>$ kümesinde olduğunu görmek kolay. Bu kümedeki her vektörün çözüm kümesinde olduğu da teoremden önceki cümleden dolayı doğru. $\quad \square$
Bir de homojen olmayan sisteme, mesela
$$\left(
\begin{array}{rrrr|r}
7& 0& -7& 0& 1\\
0& 1& 3& -2& -1\\
0& 0& -6& 2& -2
\end{array}
\right)$$
matrisiyle verilen sisteme bakalım. Çözümler $s$ bir gerçel sayı olmak üzere
$$\left(
\begin{array}{cc}
\frac{1}{3} s+\frac{1}{3}\\
s-1\\
\frac{1}{3} s+\frac{1}{3}\\
s
\end{array}
\right) = s\left(
\begin{array}{c}
\frac{1}{3}\\
1\\
\frac{1}{3}\\
1
\end{array}
\right) +
\left(
\begin{array}{c}
\frac{1}{3}\\
-1\\
\frac{1}{3}\\
0
\end{array}
\right)$$
şeklinde.
Şimdi de bu sisteme benzeyen homojen sisteme bakalım:
$$\left(
\begin{array}{rrrr|r}
7& 0& -7& 0& 0\\
0& 1& 3& -2& 0\\
0& 0& -6& 2& 0
\end{array}
\right) \ .$$
Bu sisteme yukarıdaki sisteme iliştirilen homojen sistem diyelim.
Bu sistemin çözümleri
$$s\left(
\begin{array}{c}
\frac{1}{3}\\
1\\
\frac{1}{3}\\
1
\end{array}
\right)$$
formundadır. Burada da bir düzen varmış gibi. Bunu kanıtlamadan şöyle özetleyelim:
Teorem 3. Bir lineer sistemin bir $\vec{v}_0$ çözümü verilsin. O zaman bu lineer sistemin çözümleri, $\vec{v}$ iliştirilen homojen sistemin bir çözümü olmak üzere, $\vec{v}_0+\vec{v}$ şeklindeki vektörlerdir.
Özetle: Lineer sistemleri çözmek için homojen lineer sistemleri çözmek ve her sistem için -eğer varsa- tek bir çözüm bulmak yeterli. Bir homojen lineer sistemin çözümünü de sistemin bir eşelon formundaki serbest değişkenlerinden okumak oldukça kolay.
İndirgenmiş Eşelon Form
Bir denklem sistemini eşelon forma getirmenin çözüm kümesini bulma işinde ne kadar faydalı olduğunu yukarıda gördük, fakat eşelon formla ilgili ufak birkaç sorun var. Mesela bir sisteme farklı Gauss hamlelerini uygulayarak eşelon formda iki farklı sistem elde edebiliriz. Hatta bu iki sistemdeki serbest değişkenlerin farklı olması ihtimali de var (Ama bu ihtimal gerçekleşmiyor). Bu sorunları aşmak için şu yeni kavramı tanıtalım: Eşelon formdaki bir denklem sisteminde her baş değişkenin başındaki katsayı $1$ ise ve o değişkenin bulunduğu sütundaki diğer bütün katsayılar $0$’sa, o denklem sistemine indirgenmiş eşelon formda denir.
Örneğin aşağıdaki matrisle verilen lineer sisteme bakalım:
$$\left(
\begin{array}{rrrr|r}
2& 6& 1& 2& 5\\
0& 3& 1& 4& 1\\
0& 3& 1& 2& 5
\end{array}
\right) \ .$$
İkinci satırın $-1$ katını üçüncüye ekleyelim:
$$\left(
\begin{array}{rrrr|r}
2& 6& 1& 2& 5\\
0& 3& 1& 4& 1\\
0& 0& 0& -2& 4
\end{array}
\right) \ .$$
Bu matris eşelon formda ama indirgenmiş eşelon formda değil. Şimdi ilk amacımız baş değişkenlerin katsayılarını $1$ yapmak. Bunun için de satırları sırasıyla $\frac{1}{2}$, $\frac{1}{3}$ ve $-\frac{1}{2}$ ile çarpmak yeterli. Elde ettiğimiz yeni matris şu:
$$\left(
\begin{array}{rrrr|r}
1& 3& \frac{1}{2}& 1& \frac{5}{2}\\
0& 1& \frac{1}{3}& \frac{4}{3}& \frac{1}{3}\\
0& 0& 0& 1& -2
\end{array}
\right) \ .$$
Son olarak da ikinci ve dördüncü sütunları sıfırlamak için üçüncü satırın $-\frac{4}{3}$ katını ikinci satıra ekleyelim:
$$\left(
\begin{array}{rrrr|r}
1& 3& \frac{1}{2}& 1& \frac{5}{2}\\
0& 1& \frac{1}{3}& 0& 3\\
0& 0& 0& 1& -2
\end{array}
\right) \ .$$
Birinci satıra ilk önce üçüncü satırın $-1$ katını, sonra da ikinci satırın $-3$ katını ekleyelim:
$$\left(
\begin{array}{rrrr|r}
1& 0& -\frac{1}{2}& 0& -\frac{9}{2}\\
0& 1& \frac{1}{3}& 0& 3\\
0& 0& 0& 1& -2
\end{array}
\right) \ .$$
Sütunlara karşılı gelen değişkenlere $x_1,x_2,x_3,x_4$ dersek, $x_3$’ün serbest olduğunu görürüz ve çözüm kümesini de şu şekilde yazabiliriz:
$$\left\{ \left(
\begin{array}{r}
-\frac{9}{2}\\
3\\
0\\
-2
\end{array}
\right) +
s\left(
\begin{array}{r}
\frac{1}{2}\\
-\frac{1}{3}\\
1\\
0
\end{array}
\right)\, :\, s\in \mathbb{R} \right\} \ .$$
Bazen matrislerin satırlarını, satır vektörü olarak yazarız; mesela $m\times n$’lik bir $A$ matrisini $\vec{v}_1,\ldots,\vec{v}_m$, $n$ girdili satır vektörler olmak üzere
$$\left(
\begin{array}{c}
\vec{v}_1\\
\vec{v}_2\\
\vdots\\
\vec{v}_m
\end{array}
\right)$$
olarak yazacağız. Bu yazımı kullanarak matrislerin (ya da denklem sistemlerinin) denkliğini daha cebirsel bir biçimde ifade edebiliriz. Şu matrisler verilsin:
$$A=\left(
\begin{array}{c}
\vec{v}_1\\
\vec{v}_2\\
\vdots\\
\vec{v}_m
\end{array}
\right), \quad
B=\left(
\begin{array}{c}
\vec{w}_1\\
\vec{w}_2\\
\vdots\\
\vec{w}_m
\end{array}
\right) \ .$$
Bu durumda $A$ ve $B$ matrisleri denktir (yani birbirlerinden sonlu tane Gauss hamlesiyle elde edilebilirler) ancak ve ancak her $i$ için
$$\vec{w}_i=c_{i1}\vec{v}_1+\cdots+c_{im}\vec{v}_m \quad \text{ ve } \quad \vec{v}_i=d_{i1}\vec{w}_1+ \cdots +d_{im}\vec{w}_m$$
olacak şekilde $c_{ij}$’ler ve $d_{ij}$’ler vardır.
Şimdi eşelon formdaki matrislere geri dönelim. Onları diğerlerinden ayıran şu özelliktir:
Önsav 1. Eşelon formdaki bir matrisin tümüyle $0$ olmayan satırları diğer satırların lineer kombinasyonu şeklinde yazılamaz.
Şu sonuçla bölümü bitirelim.
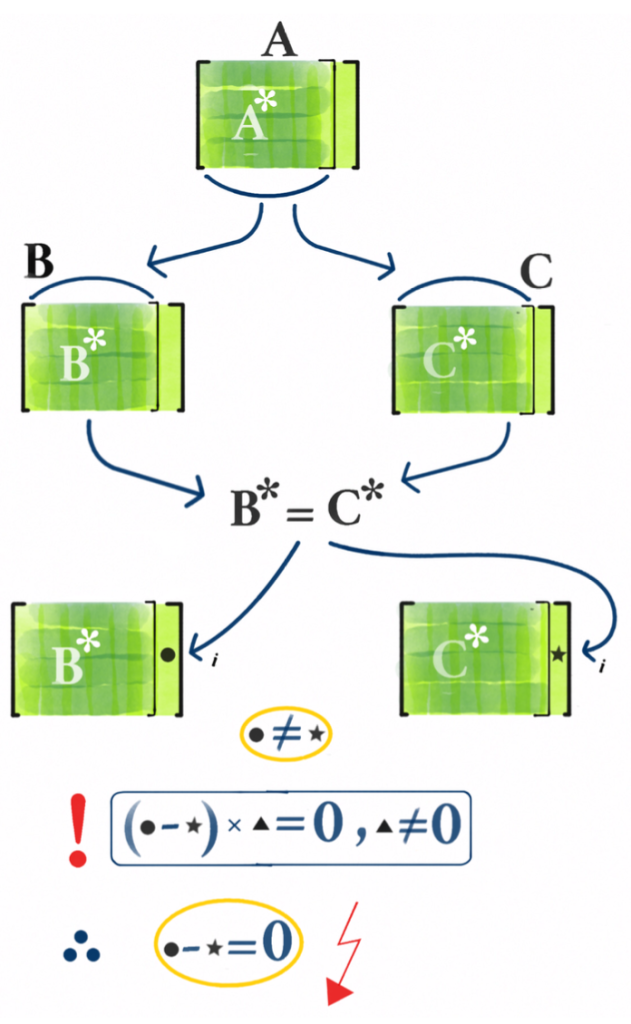
Teorem 4. Her matris bir ve yalnız bir indirgenmiş eşelon formda matrise denktir.
Kanıt. Her denklik sınıfında en az bir tane indirgenmiş eşelon formda matris olduğunu görmek çok zor değil ama üzerinde biraz düşünmek gerekebilir.
Tekliği göstermek için sütun sayısı üzerine tümevarım yapacağız. Ancak ilk olarak, $0$-matrisinin sadece kendisine denk olduğuna dikkat edelim. Yani elimizdeki matrisin $0$-matrisi olmadığını varsayabiliriz.
Tek sütunlu (yani $m\times 1$’lik) indirgenmiş eşelon formda tek matrisin, ilk girdisi $1$, diğer girdileri $0$ olan matris olduğu açık olduğundan $n=1$ adımımız barizdir.
Şimdi $n^{\prime}<n$ iken $n^{\prime}$ sütunlu her matris için bu matrise denk indirgenmiş eşelon fromda tek bir matris olduğunu varsayalım. Bir $m\times n$’lik $A$ matrisi ile bu matrise denk indirgenmiş eşelon formda $B$ ve $C$ matrisleri verilsin. Amacımız $B$ ile $C$’nin aynı matris olduğunu göstermek.
$A$’nın ilk $n-1$ sütunundan oluşan matris $A^*$ olsun. $A$’dan $B$’yi elde etmek için kullandığımız Gauss hamlelerini $A^*$’a uyguladığımızda elde ettiğimiz matris $B^*$, tam olarak $B$’nin ilk $n-1$ sütunundan oluşan matristir ve bu matris de eşelon formdadır. Benzer biçimde $C^*$’ı da tanımlarsak, tümevarım varsayımından $B^*=C^*$ olduğunu görürüz. Yani $B$ ve $C$ sadece son sütunda farklı olabilirler. Öyle olduğunu varsayalım ve -mesela- $i$’inci girdide farklı olsunlar.
Şimdi $B$ ve $C$ ile belirlenen homojen lineer denklem sistemlerine bakalım. Birbirlerine denk olduklarından bu iki sistemin çözüm kümeleri aynıdır ve indirgenmiş eşelon formun tanımından dolayı son sütunla belirlenen değişken serbest olmak zorundadır. (Aksi halde o satır, bir $1$ ve $m-1$ tane $0$ içeren bir sütun olacaktır.). Diğer yandan da bu denklem sistemlerinin $i$’inci satırı
$$b_{i1}x_1+…+b_{in}x_n=0 \quad \text{ ve } \quad c_{i1}x_1+…+c_{in}x_n=0$$
şeklinde olacaktır. Herhangi bir $\vec{s}$ çözümü alıp ilk denklemden ikincisini çıkartırsak $(b_{in}-c_{in})s_n=0$ olduğunu görürüz. Ama biz $b_{in}\neq c_{in}$ olduğunu biliyoruz. Yani $s_n=0$ olmak zorunda ve bu da $x_n$’in serbest olmasına ters düşer. Yani aslında $B=C$ olur. $\quad \square$