Bu yazıda çeşitli geometrik nesnelerin “simetri”lerini bulacağız. Her seferinde, ele aldığımız geometrik nesnenin simetriler kümesi bileşke işlemiyle birlikte bir grup olacak.
Örnek 1. Karenin Simetrileri. Bir kareyle başlayalım. Karenin köşelerini 1, 2, 3 ve 4 diye numaralandıralım. Henüz simetrinin matematiksel anlamını bilmesek de karenin simetrilerini bulacağız. Karenin simetrileri bileşke işlemi altında bir grup oluşturacak biçimde tanımlanacak. (Tanım birazdan.) Karenin simetrilerinden oluşan gruba G adını verelim.
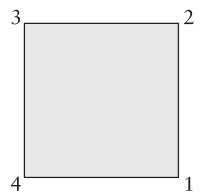
Merkezini sabit tutarak kareyi saatin (mesela) ters yönüne doğru $90$ derece döndürebiliriz. Şekilnaşağıda. Bu dönüşüme $r$ adını verelim. O zaman, sadece karenin köşelerine odaklanırsak, bu dönüşüm
$r = (1 2 3 4)$
olarak yazılır. $r$’yi iki defa da uygulayıp kareyi $180$ derece döndürebiliriz. Üç defa da uygulayabiliriz. Dört defa uyguladığımızda kare $360$ derece dönüp eski yerine gelir; yani
$r_{4} = Id_4$
olur. Demek ki $r$’nin derecesi $4$’tür. $r$’nin kendisiyle bileşkesini alarak
$Id_4$
$r$ $=(1 2 3 4)$
$r^2$ $=(1 3)(2 4)$
$r^3$ $=(1 4 3 2)$
dönüşümlerini elde ederiz. ($r_0$, tanım gereği $Id_4$ olur; dolayısıyla $r^4$ = $r^0$ = $Id_4$ ve $r^5$ = $r$, $r^6$ = $r^2$,
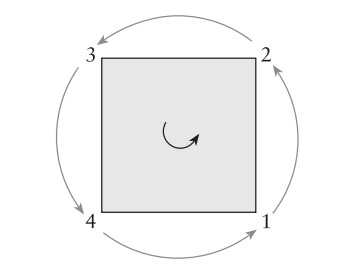
Bunlara döndürü denir. Döndürüler kümesine $R$ diyelim:
$R$$=$$\{Id_4, r, r^2, r^3\}$
$R$’nin bileşke altında kapalı olduğuna dikkat edelim. Mesela
$r^3r$ =$r^4$ = $Id_4$
ve
$r^2r^3$ = $r^5$ = $r$
olur. Ayrıca $r$’deki her elemanın bir tersi vardır ve bu ters de $R$’dedir:
$r^{-1}$ = $r^{3}$, $(r^{2})^{-1}$ = $r^{2}$, $(r^{3})^{-1}$ = $r$.
Yani $R$ bir gruptur. (Bunu sayfa 49’daki Teorem 1’den de biliyoruz.) Bir başka deyişle $R\leq G$ olur. Bu dört dönüşümü gerçekleştirmek için düzlemden çıkmaya gerek yok, kareyi düzlemde kalarak döndürebiliriz. Bu dört dönüşüm dışında karenin dört simetrisi daha vardır. Bunlardan biri aşağıdaki noktalı eksene göre ayna görüntüsüdür.
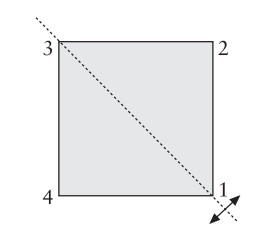
Köşelere odaklanırsak, bu dönüşümü
$s$ = $(2 4)$
permütasyonu olarak yazabiliriz. Bu tür simetrilere yansıma adı verilir. Yansımaları kareyi eğip bükmeden ve düzlemin dışına çıkarmadan fiziksel olarak gerçekleştiremeyiz. Yansımaları fiziksel olarak gerçekleştirmek için üçüncü boyutu kullanarak kareyi kaldırıp ters çevirip tekrar düzleme yatırmak gerekir. Karenin yukardaki eksen gibi üç simetri ekseni daha vardır (toplamda dört tane yani).
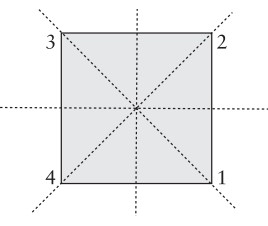
Örneğin karenin ortasından dikey inen doğru da bir simetri eksenidir; karenin bu eksene göre simetrisini alırsak $(1 2)(3 4)$ yansımasını buluruz. Karenin tüm yansımaları şöyle:
$(2 4)$ = $s$, $(1 2)(3 4)$, $(1 4)(2 3)$, $(1 3)$.
Bir yansımayı kareye iki defa peşpeşe uygularsak özdeşlik fonksiyonu $Id_4$’ü buluruz; yani yansımaların derecesi $2$’dir. Dolayısıyla yansımaların her biri $Id_4$ ile birlikte bir grup oluşturur. (Bu kadar basit bir şey için sayfa 49’daki Teorem 1’i uygulamaya gerek yok) Örneğin
$S$= {$Id_4$, $s$}
bir gruptur, yani $S ≤ G$ olur. Ama iki yansımanın bileşkesi yansıma değildir. Kontrol edildiği zaman görüleceği ve aşağıda da göreceğimiz üzere iki yansımanın bileşkesi yukarıdaki dört döndürüden biridir. $s$’yi teker teker $R$’nin dört elemanıyla (soldan ya da sağdan) çarparsak aynen yukarıda sıraladığımız 4 simetriyi elde ederiz:
$s$ $Id_4$ = $s$ = $(2 4)$ = $Id_4s$
$sr$ = $(2 4)(1 2 3 4)$ = $(1 4)(2 3)$ = $r^3$$s$
$s$$r^2$ = $(2 4)(1 3)(2 4)$ = $(1 3)$ = $r^2$$s$
$s$$r^3$ = $(2 4)(1 4 3 2)$ = $(1 2)(3 4)$ = $r$$s$.
Böylece toplam 8 tane simetri bulduk. Bu simetrilerin kümesi $D_8$ olarak gösterilir.
$D_8$ = $SR$ = $RS$ = $R\sqcup Rs$
= {$Id_4$, $r$, $r^2$, $r^3$, $s$, $rs$, $r^2s$, $r^3$$s$}.
Nitekim $R\cap S= {1}$ olduğundan, sayfa 50’deki Önsav 3’e göre $RS$’nin
$\left |R \right |\left | S \right |$$ = 4 × 2 = 8$
tane elemanı vardır. Ayrıca sayfa 50’deki Önsav 2’ye göre $D_8$ kümesi bileşke işlemi altında kapalıdır, dolayısıyla sayfa 49’daki Teorem 1’e göre bir gruptur, yani $D_8 ≤ G$ olur. (Hâlâ daha $G$’nin tanımını bilmiyoruz! Ama tanımı her ne olursa olsun, bileşke altında bir grup olacak.) $D_8$ grubunun çarpım tablosunu çizelim. $i$’inci satırdaki elemanı soldan $j$’inci satırdaki elemanla çarparsak
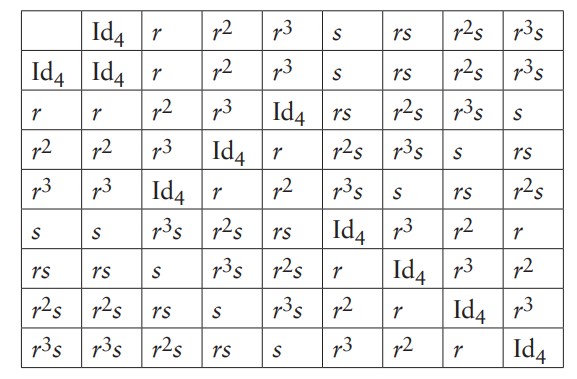
çarpım tablosunu elde ederiz. Çarpım tablosu aslında şu üç kuralla belirlenmiştir:
$r^4 = Id_4, s^2 = Id_4, sr = r^3s$.
Nitekim bu kuralları bilirsek, grupların birleşme özelliğini kullanarak, istediğimiz elemanla istediğimiz elemanı çarpabiliriz. Örneğin
$(r^2s)(rs) = r^2(sr)s = r^2(r^3s)s = r^5s^2 = r^5 = r^4r = r$
ya da
$rs(r^3) = r(sr)r^2 = r(r^3s)r^2 = r^4(sr)r = r^4(r^3s)r$
$= r^7(sr) = r^7(r^3s) = r^{10}s = r^2s$
Bu grup 8 elemanlı dihedral grup olarak adlandırılır ve biraz önce de dediğimiz gibi $D_8$ olarak gösterilir.
Bir kareyi, bir eğriyi ya da genel olarak fiziksel bir nesneyi resmetmek kolaydır, fotoğrafı bile çekilebilir ama bir grubu resmetmek kolay değildir. Daha çok hareketi temsil ettiğinden, bir grubun her elemanının ancak filmi çekilebilir, bir grup da o zaman bir film arşivi olur! Bir yazıda bu mümkün değildir. Ama biz gene de grupların resmini çizmeye çalışacağız. $D_8$’i şöyle çizeceğiz:
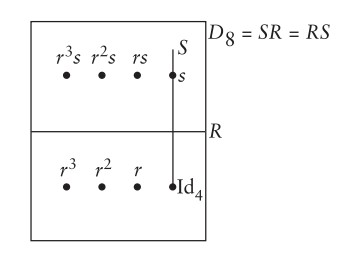
Karenin başka simetrisi yoktur. Bunu kanıtlamak için simetrinin tanımını bilmemiz lazım. Çeşitli tanımlar verilebilir. Biz şu tanımı tercih edeceğiz: Karenin simetrisi köşelerin bir permütasyonudur, ama herhangi bir permütasyonu değil, bağlantılı köşeleri bağlantılı köşelere götüren bir permütasyonudur. Örneğin yukardaki notasyonla, karenin bir simetrisi, 1 köşesini 3 köşesine götürüyorsa, 2 köşesini ya kendisine ya da 4 köşesine götürmek zorundadır, çünkü 2 köşesi 1 köşesine bağlantılıdır; dolayısıyla 2’nin gittiği köşe, 1’in gittiği köşeye (örneğimizde 3 köşesine) bağlantılı olmak zorundadır. Bu tanımla karenin yukarıdaki 8 simetriden başka simetrisi olmadığını kanıtlayalım. $G$, karenin simetrilerinden oluşan küme olsun. $G$ elbette $Sym 4$’ün bir altkümesidir ve $D_8$’i içerir. $G$’nin bileşke altında kapalı olduğu simetrinin tanımından belli. Sayfa 49’daki Teorem 1’e göre $G$ bileşke işlemiyle birlikte bir gruptur.
Rastgele bir $g\in G$ alalım. Bu $g$ elemanının $D_8$’in yukarıda sıraladığımız 8 permütasyonundan biri olduğunu kanıtlayacağız. Önce şu saptamayı yapalım: $R$’nin
$r^0$={$Id_4$, $r$, $r^2$, $r^3$}
elemanları $1$ köşesini sırasıyla $1$, $2$, $3$ ve $4$ köşesine götürür. Demek ki bir ve bir tek $i \in$$\{0, 1, 2,3\}$ için
$g(1)$=$r^i(1)$
olur. (Aslında $i$ = $g(1)$ $- 1$ olur ama bunun bir önemi yok.)
Şimdi $r^{-i}g$ permütasyonuna bakalım. Bu permütasyon da $G$’dedir, yani karenin bir simetrisidir, çünkü ne de olsa karenin simetrilerinin bileşkesidir. Ama en başta aldığımız $g$ simetrisi $1$’i rastgele bir köşeye götürürken, bu simetri $1$’i $1$’e götürür:
$(r^{-i}g)(1)$ $=1$.
Eğer tabiri caizse $r^{-i}g$ simetrisi $g$ permütasyonundan daha evcildir.
Şimdi de $(r^{-i}g)(2)$ köşesine bakalım. $1$ ile $2$ köşeleri karede bağlantılı olduklarından, $(r^{-i}g)(1)$ = 1 ile $(r^{-i}g)(2)$ köşeleri de bağlantılı olmalılar. Ama $1$’e bağlantılı olan sadece $2$ ve $4$ köşeleri var. Demek ki
ya $(r^{-i}g)(2)$$=2$ ya da $(r^{-i}g)(2)$$=4$
Şimdi $s$’nin $1$ köşesini sabitlediğini ve $2$ ve $4$ köşelerinin yerlerini değiştirdiğini gözlemleyelim. Eğer $(r^{-i}g)(2)$ = 2 ise $r^{-i}g$ simetrisi 1 ve 2 noktalarını sabitler. Eğer $(r^{-i}g)(2)$$= 4$ ise, bu sefer $sr^{-i}g$ simetrisi $1$ ve $2$ noktalarını sabitler. Demek ki birinci durumda $s^{0}r^{-i}g$ simetrisi, ikinci durumda $s^{1}r^{-i}g$ simetrisi $1$ ve $2$ noktalarını sabitler. Bir ve bir tek $j\in$ $\{0,1\}$ için $s^{j}r^{-i}g$ simetrisinin $1$ ve $2$ noktalarını sabitlediğini gösterdik. Ve $s^{j}r^{-i}g$ hâlâ daha karenin bir simetrisidir, yani hâlâ $G$’dedir.
Son olarak $1$ ve $2$ noktalarını sabitleyen karenin bir simetrisinin özdeşlik fonksiyonu olması
gerektiğini kanıtlayalım. Bunu kanıtlarsak,
$s^{1}r^{-i}g$ $=Id_4$
ve dolayısıyla
$g$=$r^{i}(s^{j})^{-1}$=$r^{i}s^{j}$ $\in$ $D_8$
olur ve istediğimiz kanıtlanmış olur.$t$ $\in$ $G$ simetrisi $1$ ve $2$ noktalarını sabitlesin. $2$ ve $3$ noktaları bağlantılı olduklarından, $t(3)$ noktası $t(2)$ $=2$ noktasına bağlantılı olmalıdır. Demek ki ya $t(3)$ $= 1$ ya da $t(3)$ $= 3$. Ama zaten $t(1)$ $= 1$. Demek ki $t(3)$ $= 1$ olamaz ve $t(3)$ $= 3$ olmalı. Şimdi $t$ simetrisi $1$, $2$ ve $3$ noktalarını sabitliyor. Geriye kalan son noktanın kendisinden başka gidecek yeri kalmamıştır. Böylece $t$ $= Id_4$ ve $G$ $= D_8$ eşitlikleri kanıtlanmış oldu.
Örnek 2. Üçgen Tabanlı Piramidin Simetrileri.
Bu sefer üç boyutlu bir nesne alalım: Üçgen tabanlı düzgün piramit.
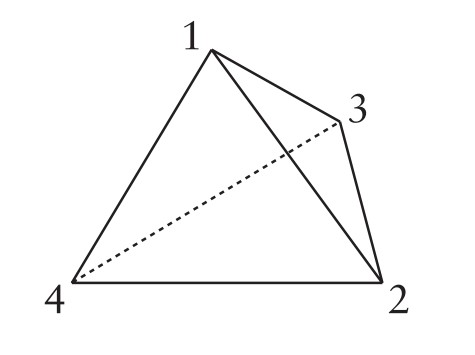
Köşelerden birinden, diyelim $1$ noktasından, bu noktanın karşısındaki yüzeye dik bir doğru geçirelim. Bu doğruyu eksen kabul eden $120$ derecelik bir döndürü vardır ve bu döndürü elbette piramitin bir simetrisidir. Bu döndürüyü $r_1$ olarak gösterelim.
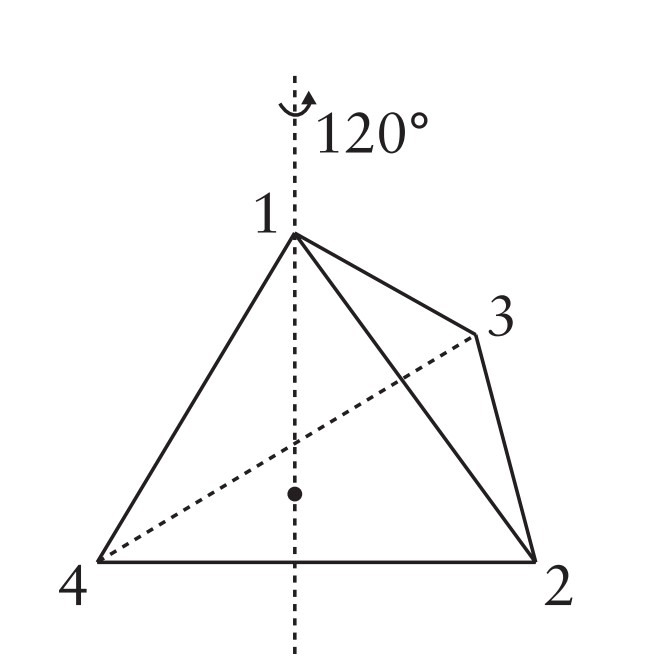
Şekilden de görüleceği üzere, köşelere odaklanırsak,
$r_{1}$ =($2$ $3$ $4$)
olur. $r_{1}$’in kendisiyle bileşkesini alabiliriz:
$r_{1}$ =($2$ $3$ $4$), $r_{1}^2$ =($2$ $4$ $3$), $r_{1}^3$ = $Id_4$.
Aynen bu $r_{1}$ gibi, $r_{2}$, $r_{3}$, $r_{4}$ simetrilerini de bulabiliriz:
$r_{2}$ =($1$ $4$ $3$), $r_{3}$ =($1$ $2$ $4$), $r_{4}$ =($1$ $3$ $2$).
Böylece toplam 9 tane simetri bulduk: $Id_4$ ve
$r_{1}$ =($2$ $3$ $4$), $r_{1}^2$ =($2$ $4$ $3$),
$r_{2}$ =($1$ $4$ $3$), $r_{2}^2$ =($1$ $3$ $4$),
$r_{3}$ =($1$ $2$ $4$), $r_{3}^2$ =($1$ $4$ $2$),
$r_{4}$ =($1$ $3$ $2$), $r_{4}^2$ =($1$ $2$ $3$),
Çok daha fazlasını bulacağız. Şimdilik, $i$ = $1$, $2$, $3$, $4$ için
$R_{i}$=$\{Id_{4},r_{i},r_{i}^{2}\}$
tanımını yapalım. $R_{i}$, bileşke işlemi altında bir gruptur. Başka simetriler bulmaya çalışalım. Kesişmeyen iki kenarın orta noktalarını birleştiren
doğruyu alalım. Piramiti bu doğru etrafında $180$ derece döndürebiliriz.
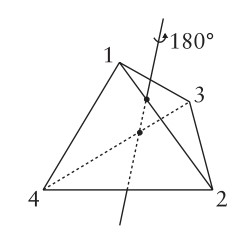
Şekildeki döndürüyü yaparsak
$a_{2}$=$( 1 2 )$$( 3 4 ) $
permütasyonunu buluruz. Bunun gibi iki tane daha vardır. Her birini yazalım:
$a_{2}$=$( 1 2 )$$( 3 4 ) $,
$a_{3}$=$( 1 3 )$$( 2 4 ) $,
$a_{4}$=$( 1 4 )$$( 2 3 ) $,
imdi çok tuhaf bir şey söyleyeceğim:
$A=$ {$Id_4$, $a_2$, $a_3$, $a_4$}
kümesi bileşke işlemiyle birlikte bir grup olur. (Bu tuhaf olgu sadece 4 sayısına özgüdür.) Hatta bir abel grubu olur. Okur bunu kolaylıkla kontrol edebilir ama biz de kontrol edelim:
$a_{2}a_{3}$= $\left|(1 2)(3 4) \right|$ $\left|(1 3)(2 4) \right|$= $(1 4)$$(23)$=$a_4$
Benzer eşitlik diğerleri için de geçerlidir:
$a_{2}$$a_{3}$=$a_{3}$$a_{2}$=$a_{4}$,
$a_{2}$$a_{4}$=$a_{4}$$a_{2}$=$a_{3}$,
$a_{3}$$a_{4}$=$a_{4}$$a_{3}$=$a_{2}$.
Ayrıca $A$ kümesinin her elemanı kendisinin tersidir. Ve
$A$ $\cap$ $R_{1}$=$\{Id_4\}$
olur. Nitekim sayfa 50’deki Önsav 3’e göre
$\left| AR_{1}\right|$=$\left| A\right|$$\left| R_{1}\right|$=$4\times 3$=$12$
olmalıdır. $AR_{1}$ kümesinin elemanları şimdiye kadar bulduğumuz
$Id_{4}$,$ r_{1}$, $r_{1}^{2}$,$r_{2}$, $r_{2}^{2}$, $r_{3}$, $r_{3}^{2}$,$r_{4}$,$r_{4}^{2}$, $a_{2}$, $a_{3}$,$a_{4}$
elemanlarıdır. Gerçekten de,
$a_{2}$$r_{1}$= $(1 2)(3 4)(2 3 4)$=$(1 2 4)$=$r_{3}$,
$a_{2}$$r_{1}^{2}$= $(1 2)(3 4)(2 4 3)$=$(1 2 3)$=$r_{4}^{2}$,
$a_{3}$$r_{1}$= $(1 3)(3 4)(2 3 4)$=$(1 3 2)$=$r_{4}$,
$a_{3}$$r_{1}^{2}$= $(1 3)(2 4)(2 4 3)$=$(1 3 4)$=$r_{2}^{2}$,
$a_{4}$$r_{1}$= $(1 4)(2 3 )(2 3 4)$=$(1 4 3)$=$r_{2}$,
$a_{4}$$r_{1}^{2}$= $(1 4)(2 3)(2 4 3)$=$(1 4 2)$=$r_{3}^{2}$
eşitliklerinden
$AR_{1}$=$A\sqcup$ $Ar_{1}$$\sqcup Ar_{1}^{2}$ ={$Id_{4}$,$ r_{1}$, $r_{1}^{2}$,$r_{2}$, $r_{2}^{2}$, $r_{3}$, $r_{3}^{2}$,$r_{4}$,$r_{4}^{2}$, $a_{2}$, $a_{3}$,$a_{4}$}
eşitliğini buluruz. Bu kümeye $H$ adını verelim:
$H$=$AR_{1}$
Benzer şekilde $R_{1}$$A$ = $H$ eşitliğini kanıtlayabiliriz:
$r_{1}$$a_{2}$= $(2 3 4)(1 2)(3 4)$=$(1 3 2)$=$r_{4}$,
$r_{1}^{2}$$a_{2}$= $(2 4 3)(1 2)(3 4)$=$(1 4 2)$=$r_{3}^{2}$,
$r_{1}$$a_{3}$= $(2 3 4)(1 3)(2 4)$=$(1 4 3)$=$r_{2}$,
$r_{1}^{2}$$a_{3}$= $(2 4 3)(1 3)(2 4)$=$(1 2 3)$=$r_{4}^{2}$,
$r_{1}$$a_{4}$= $(2 3 4)(1 4)(2 3)$=$(1 2 4)$=$r_{3}$,
$r_{1}^{2}$$a_{4}$= $(2 4 3)(1 4 )(2 3)$=$(1 3 4)$=$r_{2}^{2}$.
Demek ki sayfa 50’deki Önsav 2’ye göre $H$ bileşke altında kapalıdır ve sayfa 49’daki Teorem 1’e göre bir gruptur. Şekli aşağıda
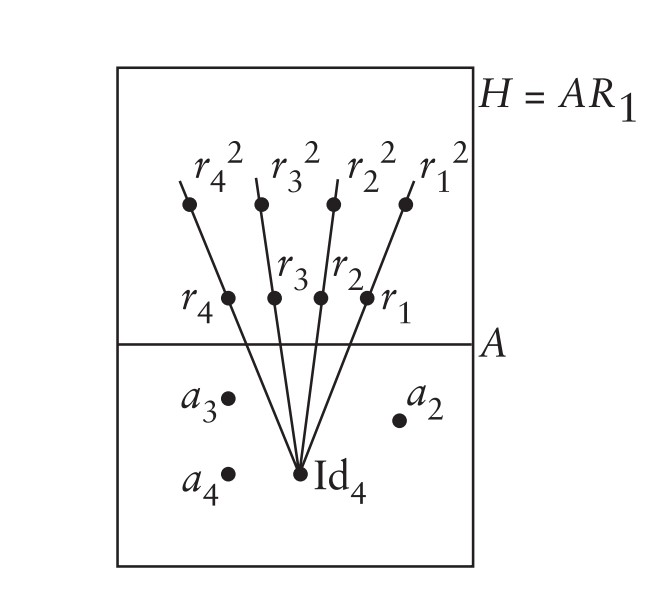
$H$’nin her elemanının piramitin bir simetrisi olduğunu biliyoruz. (Simetriyi bir önceki örnekteki gibi tanımlıyoruz.) Yani eğer $G$ piramitin simetrilerinden oluşan grupsa, $H\leq G$ olur. Piramitin daha fazla simetrisi vardır, ama diğerleri piramidi eğip bükmeden üç boyutlu uzayda fiziksel olarak gerçekleştirilemezler. Nitekim piramitin karşılıklı iki kenarından birini içeren, diğerinin orta noktasından geçen düzleme göre simetrisini (ayna görüntüsünü) alabiliriz.
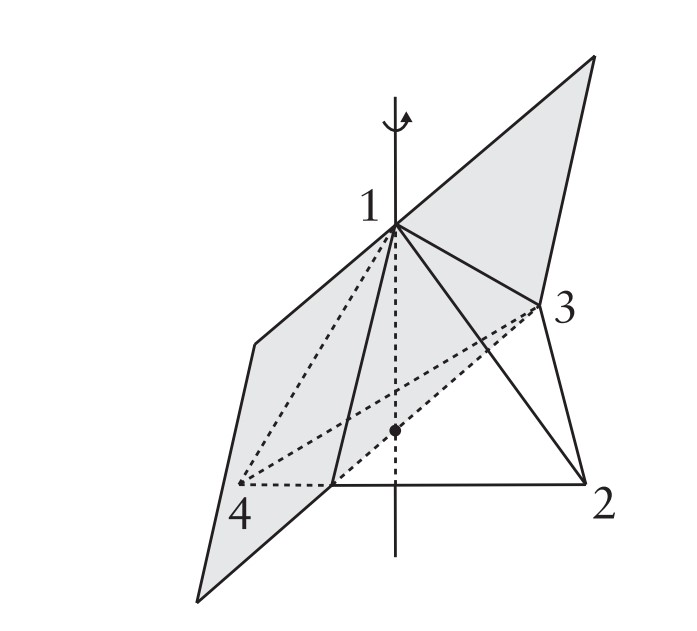
Yukarıdaki şekildeki örnekte
$t$=$(1 4)$
simetrisini elde ederiz. $t^2$ = $Id_4$ olur elbette. Her ne kadar $t$ dönüşümü üç boyutlu uzayda gerçekleştirilemiyorsa da, $t$ piramitin bir simetrisidir, ama $H$’de değildir (çünkü $t$ dönüşümü sağı sol, solu sağ yapar, oysa uzayda istediğiniz kadar dolaşın sağınız solunuza, solunuz sağınıza gelmez).
$T$= $\{Id_{4}, t\}$
olsun. $T$bir gruptur ve $H \cap T$= ${Id_{4}}$ olur. Demek ki sayfa 50’deki Önsav 3’e göre
$\left|H T \right|$=$\left| H\right|$$\left| T\right|$=$12\times 2$=$24$
olur. Ama $HT$$\subseteq$ $Sym4$ ve her ikisinin de $24$ elemanı var Demek ki
$G$=$HT$=$Sym4$.
$H$’nin elemanları sağı solu koruduğundan, $t$ ise sağı sol yaptığından, $Ht$ kümesinin elemanları sağı sol yaparlar, dolayısıyla üç boyutlu uzayda çekip
çekiştirmeden gerçekleştirilemezler. $H$’nin elemanları (12 tane) uzayda gerçekleştirilebilirler. İleride $H$’nin Alt 4 olarak adlandırılan önemli bir grup
olduğunu göreceğiz.
Örnek 3. Piramitin Simetrileri. Bu sefer tabanı düzgün n-gen olan bir dik piramit alalım. $n = 3$ durumunu yukarda görmüştük. Şimdi $n > 3$ durumuna bakalım.
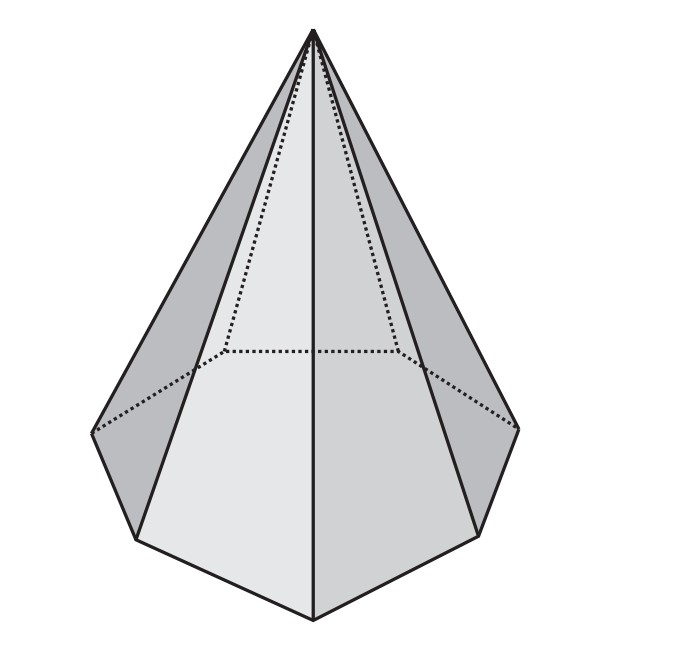
Tabandaki noktaların üç bağlantısı vardır; yani dereceleri $3$’tür. Oysa tepe noktasının derecesi $n$’dir. Tepe noktası derecesi $n$ olan yegâne nokta olduğundan, her simetri tepe noktasını tepe noktasına götürmek zorundadır. Dolayısıyla eğer istersek tepe noktasını unutup düzgün bir n-gen olan
tabanın simetrilerine odaklanabiliriz. (Tabanın her simetrisi piramitin bir simetrisine genişletebilir ve piramitin her simetrisi tabanın bir simetrisini verir.)
Bildiğimiz simetrileri yazalım. Öncelikle tepe noktasını sabitleyen döndürüler var. Eğer $r$ en küçük pozitif açılı döndürüyse, toplam $n$ tane döndürü elde ederiz:
$R$={$1$,$r$,$r^{2}$, …,$r^{n-1}$}.
Bunların dışında bir de tabanın farklı eksenlere göre ayna simetrileri vardır. Bunlardan da tam $n$ tane vardır, ama eğer $s$ bunlarsan biriyse,
$Rs$
kümesi tüm ayna simetriler kümesidir. Piramitin simetriler grubu
$D_{2n}$=$R$ $\sqcup$ $Rs$
dir ve bu simetrilerin sadece yarısı ($R$’deki döndürüler) üç boyutlu uzayda gerçekleştirilebilir. Bunun böyle olduğunun kanıtını okura bırakıyoruz. Çarpım tablosu da
$r^{n}$=$Id$, $s^{2}$=$Id$ ve $sr$=$r^{n-1}s$
eşitlikleri tarafından belirlenir. $D_2n$ grubuna, $2n$ elemanlı dihedral grup adı verilir.
Örnek 4. Küpün Simetrileri. Köşelerini aşağıdaki şekildeki gibi 1’den 8’e kadar adlandırdığımız küpün simetrilerini bulacağız.
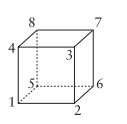
Küpü bize doğru gelen eksen üzerinde saatin ters yönünde 90 derece döndürebiliriz.
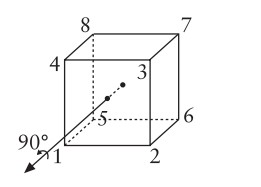
Bu dönüşüme $r$ diyelim. Köşeler $r$ altında şöyle dönüşür:
$r$=$(1 2 3 4)$$(5 6 7 8)$.
Tabii $r$’nin kuvvetlerini alırsak,
$r^{0}$=$Id_{8}$
$r^{1}$=$r$=$(1 2 3 4)$$(5 6 7 8)$
$r^{2}$=$(1 3)$$(2 4)$$(5 7)$$(6 8)$
$r^{3}$=$(1 4 3 2)$$(5 8 7 9)$
buluruz. $r^{4}$=$Id_{8}$ olur.
$R$={$Id_{8}$, $r$,$r^{2}$, $r^{3}$}
olsun. $R$ bileşke işlemi altında bir gruptur.Bir de ön yüzle arka yüzü ayna görüntüsü sayesinde değiştirebiliriz.
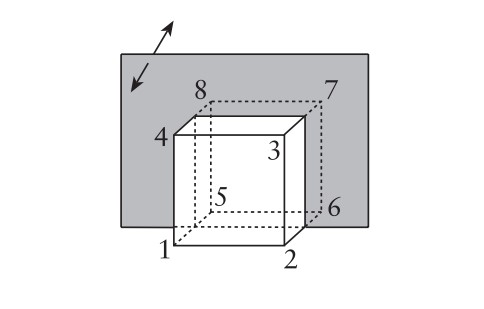
Bu dönüşümü $s$ olarak gösterelim:
$s$=$(1 5)$$(2 6)$$(3 7)$$(4 8)$.
Tabii $s^{2}$=$Id_{8}$ olur.
S=$\{ Id_{8}, S\}$
olsun. $S$ de bileşke işlemi altında bir gruptur. Ama $RS$ de bir gruptur. Nitekim,
$srs$=$(1 5)$$(2 6)$$(3 7)$$(4 8)$$(1 2 3 4)$$(5 6 7 8)$$(1 5)$$(2 6)$$(3 7)$$(4 8)$=$(1 2 3 4)$$(5 6 7 8)$=$r$
olduğundan, $sr$ = $rs$ olur ve Sayfa 50, Önsav 2’ye göre $RS$ bir gruptur, hatta değişmeli bir gruptur. $RS$ grubunun tam 8 elemanı vardır:
$Id_{8}$
$r$=$(1 2 3 4)$$(5 6 7 8)$
$r^{2}$=$(13)$$(2 4)$$(5 7)$$(6 8)$
$r^{3}$=$(1 4 3 2)$$(5 8 7 6)$
$s$=$(1 5)$$(2 6)$$(3 7)$$(4 8)$
$rs$=$(1 2 3 4)$$(5 6 7 8)$$(1 5)$$(2 6)$$(3 7)$$(4 8)$$=$(1 6 3 8)$$(2 7 4 5)$
$r^{2}$$s$=$(13)$$(2 4)$$(5 7)$$(6 8)$$(1 5)$$(2 6)$$(3 7)$$(4 8)$=$(1 7)$$(2 8)$$(3 5)$$(46)$
$r^{2}$$s$=$rs^{-1}$=$(1 8 3 6)$$(2 5 4 7)$
$RS$’nin 8 tane elemanı olduğu sayfa 50’deki Önsav 3’ten de belli.
Dikkat ederseniz $i$ = $1$, …, $8$ verilmişse, $1$ köşesini $i$ köşesine götüren bir ve bir tane $g$$\in$ $RS$ var. Mesela $1$’i $6$’ya sadece $rs$ $\in$ $R$$S$ götürüyor, $1$’i $1$’e sadece $Id_8$ $\in$ $R$$S$ götürüyor.
Yukarıda yaptıklarımızı aklımızın bir köşesinde tutup küpün başka simetrilerini bulmak amacıyla yola koyulalım. Bunu yapmak için küpün köşelerini 1, 2 gibi sayılarla değil, aşağıdaki gibi 01-üçlüleriyle gösterelim.
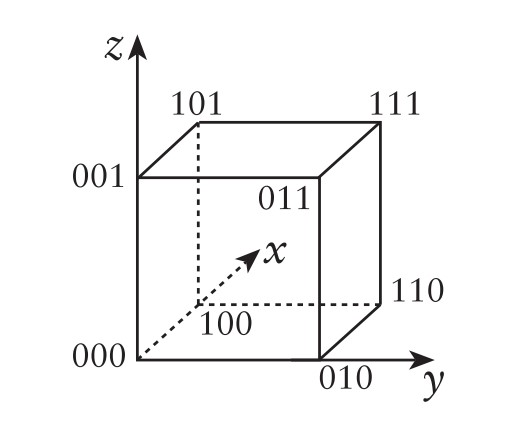
Dikkat ederseniz iki köşenin birbiriyle bağlantılı olması için yeter ve gerek koşul iki köşenin sadece tek bir teriminin farklı olmasıdır. Örneğin $010$ ile $011$ bağlantılıdır, çünkü sadece son terimleri farklıdır. Bunun gibi $110$ ile $100$ bağlantılıdır ama $010$ ile $001$ bağlantılı değildir. Hatta iki noktanın farklı terim sayısı iki nokta arasındaki mesafedir: $100$ noktasından $011$ noktasına gitmek için 3 kenardan geçmek gerekir, daha az kenardan geçerek
gidemeyiz.
Bir önceki paragraftaki açıklamalardan dolayı, koordinatların yerlerini değiştirmek küpün bağlantılılık ilişkisini bozmaz. Örneğin, birinci ve ikinci
koordinatların yerlerini değiştirirsek, küpün
$000$$\mapsto$$000$
$001$$\mapsto$$001$
$010$$\mapsto$$100$
$011$$\mapsto$$101$
$100$$\mapsto$$010$
$101$$\mapsto$$011$
$110$$\mapsto$$110$
$111$$\mapsto$$111$
dönüşümünü elde ederiz, ki bu dönüşüm bağlantılı noktaları bağlantılı noktalara, bağlantısız noktaları bağlantısız noktalara götürür Ya da birinci koordinatı ikinci koordinata, ikinci koordinatı üçüncü koordinata, üçüncü koordinatı birinci koordinata yollayabiliriz. O zaman,
$000$$\mapsto$$000$
$001$$\mapsto$$100$
$010$$\mapsto$$001$
$011$$\mapsto$$101$
$100$$\mapsto$$010$
$101$$\mapsto$$110$
$110$$\mapsto$$011$
$1111$$\mapsto$$111$
dönüşümünü elde ederiz. Böylece, koordinatların her dönüşümü bize küpün bir simetrisini verir ve bunlardan da $3!$ = $6$ tane vardır, $Sym 3$’ün eleman sayısı kadar. Bu dönüşümlerin kümesine $T$ adını verelim. T elbette bir gruptur. ($Sym 3$ ‘e çok benzer)
$T$’nin elemanlarının her biri $000$ köşesini (yani yukarıdaki yazılımla $1$ köşesini) sabitler. Daha önce bulduğumuz $RS$ grubunun sadece $Id_8$ elemanı $1$köşesini sabitlediğinden
$T$$\cap$ $R$ = $Id_{8}$
olur. Buradan da, sayfa 50’deki Önsav 3’e göre, $RST$ kümesinin
$\left|RS \right|$$\times$$\left| T\right|=$8$\times$$6$=$48$
elemanı olduğu çıkar.
Küpün $RST$’nin elemanlarından başka bir simetrisinin olmadığını kanıtlayalım. $g$, küpün herhangi bir simetrisi olsun. $RS$ grubunun her elemanının $1$ köşesini bir başka köşeye götürdüğünü anımsayalım. $RS$’de $1$ köşesini $g(1)$ köşesine götüren bir ve bir tane $a$ elemanı vardır. O zaman
$a^{-1}g$
simetrisi $1$ köşesini $1$ köşesine götürür. Ama $1$ köşesini $1$ köşesine götüren her simetri $T$’de olmak zorundadır. (Neden?) Demek ki bir ve bir tane $t$$\in$ $T$ için
$a^{-11}$$g$=$t$
yani
$g$=$at$
olur. Böylece küpün tüm simetrileri $RST$ kümesindedir. Böylece küpün toplam 48 tane simetrisi olduğunu gördük.
Soru: Küpün köşelerini 01-üçlüleri olarak gösterelim. Her 0 koordinatını 1’e, her 1 koordinatını da 0’a dönüştüren simetri $G$ = $RST$ grubunda nasıl yazılır?
Örnek 5. [Dört Boyutlu Küpün Simetrileri.]
Önce dört boyutlu küpü tanımlayalım. Ama daha önce 0, 1, 2 ve 3 boyutlu küpün tanımlarına bir başka gözle bakalım.
0 boyutlu küp bir noktadan ibarettir. Çizmeyi gerek görmüyoruz.
1 boyutlu küpü [0,1] aralığı olarak görebiliriz. Köşe noktaları 0 ve 1’dir.

1 boyutlu küpü şöyle de gösterebiliriz: İki tane 0 boyutlu (yani iki nokta) alıp noktaları bir doğruyla birleştirmek.

2 boyutlu küpü, köşeleri (0,0), (1,0), (0,1), (1,1) noktalarına gelecek biçimde yerleştirelim.
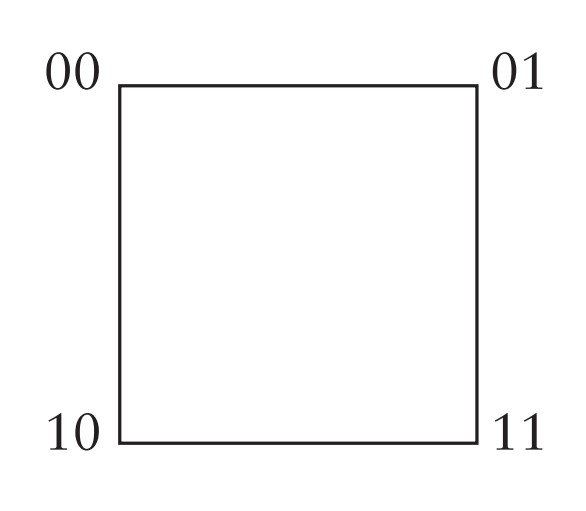
Bunu şöyle de gösterebiliriz. İki tane $1$ boyutlu küple (yani iki tane $[0,1]$ doğru parçasıyla) başlayalım. (Bkz. aşağıdaki soldaki şekil.) Sonra $1$ boyutlu küplerden birinin koordinatlarının başına $0$, diğerinin başına $1$ getirelim ve birbirine tekabül eden noktalarını bir doğruyla birleştirelim. (Bkz. aşağıdaki sağdaki şekil. Elde edilen şeklin bir kare olmaması sizi rahatsız etmesin, kare de yapabilirdik.)
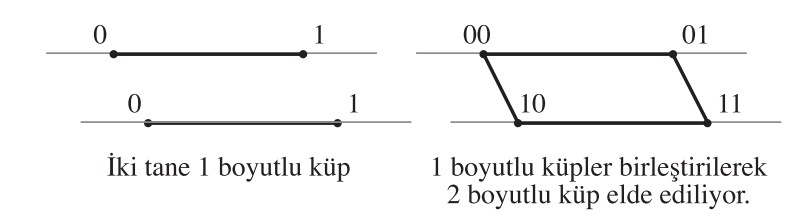
$3$ boyutlu küpü, $\mathbb{R}^{3}$uzayına yukardakine benzer şekilde, köşeler $i$, $j$, $k$ = $0$, $1$ için $(i, j, k)$ ya da daha basit olarak $ijk$ noktalarına gelecek şekilde yerleştirelim. (Aşağıdaki sağdaki şekil.) Eğer iki noktanın üç koordinatından sadece biri değişikse, köşeler arasına bir kenar çiziyoruz.
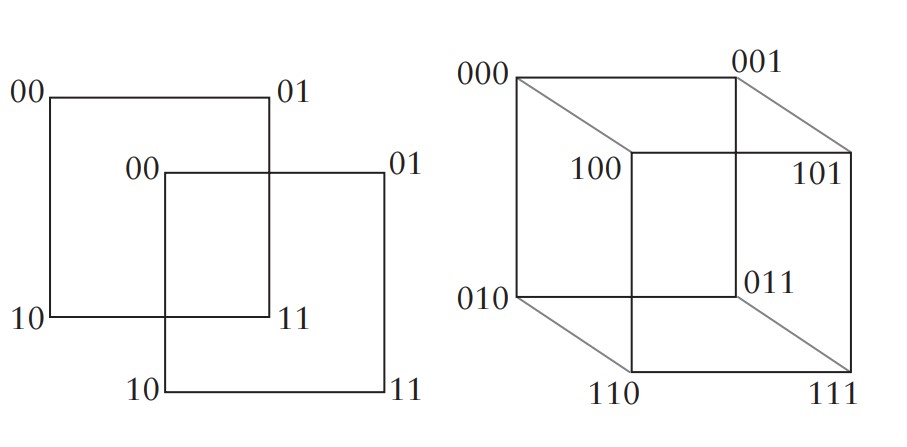
Bunu şöyle de gösterebiliriz. İki tane $2$ boyutlu küple (yani iki tane kareyle) başlayalım. (Bkz. yukarıdaki soldaki şekil.) Sonra $2$ boyutlu küplerden birinin koordinatlarının başına $0$, diğerinin başına$1$ getirelim ve birbirine tekabül eden noktalarını
bir doğruyla birleştirelim. (Bkz. yukarıdaki şekil.)
Şimdi $4$ boyutlu küpü betimleyebiliriz. İki tane üç boyutlu küp alalım. Bunlardan birinin koordinatlarının başına $0$, diğerinin başına $1$ getirelim ve küplerin birbirine tekabül eden köşelerini bir kenarla birleştirelim.
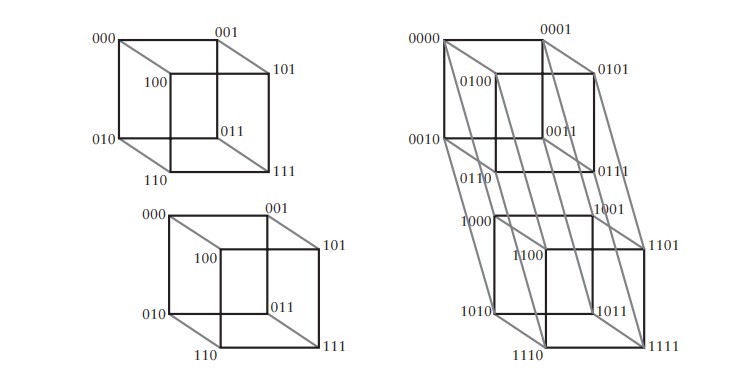
Dikkat ederseniz, iki nokta sadece tek bir koordinatta ayrışıyorsa birbiriyle bağlantılıdır. Böylece geometriyi cebirselleştirmiş olduk.
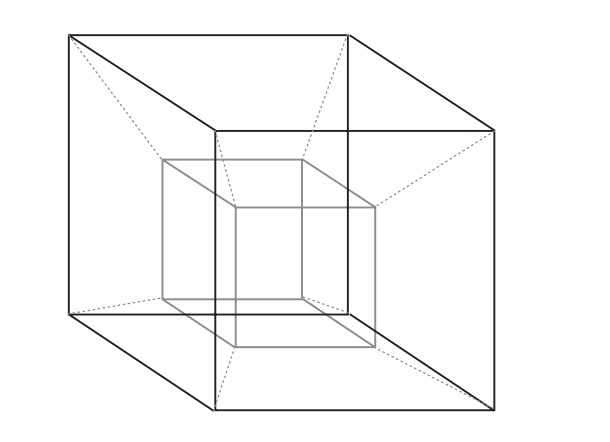
Dört boyutlu küpe $K$ adını verelim. $K$’nın simetrilerini bulalım. $K$’nın simetrilerinden oluşan gruba $G$ adını verelim.
$K$’nın başında $0$ olan noktaları üç boyutlu bir küp oluştururlar. Bu küpe $K_0$ diyelim. Başında $1$ olanlara da $K_1$ diyelim.
Bir önceki örnekte bulduğumuz üç boyutlu küpün $RS$ simetrilerini ele alalım. Anımsarsanız $RS$, 8 elemanlı bir gruptu ve üç boyutlu küpün herhangi bir noktasını $RS$’nin elemanlarıyla üç boyutlu küpün herhangi bir noktasına götürebiliyorduk. Eğer $RS$’deki simetrileri aynı anda $K_0$ ve $K_1$ küplerine uygularsak (birinci koordinata dokunmadan),$K$’nın simetrilerini buluruz. $K$’nın bu simetri grubuna da üç boyutlu küpte olduğu gibi $RS$ adını verelim.
Bir de $K_0$ ile $K_1$ değiştokuş eden bir $t$ ayna
simetrisi bulalım. Mesela $t$, noktaların birinci koordinatını değiştirsin, $0$ ise $1$, $1$ ise $0$ yapsın. $t_2$ = $Id_{16}$ olduğundan,
$T= $$\{Id_{16},t\}$
kümesi bir gruptur. $RS$ $\cap$ $T =$ $\{Id_{16}\}$ olduğundan,
$\left|RST \right|$=$\left|RS \right|$$\times$$\left| T\right|=$8$ \times$ $2$=$16$
Kolay bir hesapla görüleceği üzere $RST$ değişmeli bir gruptur.
Ayrıca $RST$ kümesinin, $K$’nın herhangi bir noktasını istediğimiz herhangi bir noktasına götürecek
bir ve bir tane elemanı vardır.
Yukarıdaki paragrafta bulunan $RST$ simetrileri dışında, $K$’nin dört koordinatını karan ve bu yüzden $Sym 4$’e çok çok benzeyen bir simetri grubu vardır. Bu simetri grubuna $U$ adını verelim: mesela
$\sigma = ( 1 2 3 )$
permütasyonuysa,
$\sigma = (i,j,k,l )=(k,i,j,l)$
olur.
$U$’nun her elemanı $(0,0,0,0)$ noktasını sabitlediğini, ama $RST$’nin sadece $Id_{16}$ elemanı bu noktayı sabitlediğinden,
$RST$$\cap$$U$$=$\{Id_{16}\}$
olur. Buradan da
$\left | RSTU \right |$$=$$\left | RST \right |$$\times$$ \left | U \right |$$=$$16$$\times$$ 4!$$=$$2^4$$ \times$$ 4!$
çıkar. Ayrıca $U$’nun elemanları
$A_1$$=$$(1,0,0,0)$
$A_2$$=$$(0,1,0,0)$
$A_3$$=$$(0,0,1,0)$
$A_4$$=$$(0,0,0,1)$
elemanlarını birbirine götürür, hatta $U$’nun elemanları bu noktalara olan etkileriyle betimlenirler.
Böylece, $RSTU$$\subseteq$ $G$ olduğundan, G’nin tam $16$$\times$$4!$ tane elemanını bulduk.
Şimdi $G$$=$$RSTU$ eşitliğini kanıtlayalım.
$g$$\in$$G$ rastgele bir eleman olsun. $RST$ grubunda,
$g$$(0,0,0,0)$$=$$\alpha$$(0,0,0,0)$
eşitliğini sağlayan bir ve bir tane $\alpha$ elemanı vardır. Şimdi
$\alpha^{-1}$$g$
elemanı $(0, 0, 0, 0)$ noktasını sabitler. Ve bu yüzden de $K$’nın dört eksenini birbirine dönüştürür. $U$ grubunda, eksenleri ya da (aynı şey) $A_1$, $A_2$, $A_3$, $A_4$ noktalarını aynen $\alpha^{-1}$$g$ elemanı gibi dönüştüren bir $\sigma$ elemanı vardır. Demek ki, $G$’nin
$\sigma^{-1}$$\alpha^{-1}$$g$
elemanı
(0,0,0,0) ve $A_1$, $A_2$, $A_3$, $A_4$
noktalarını sabitler. Böyle bir eleman tüm noktaları sabitlemek, yani $Id_{16}$’ya eşit olmak zorundadır. Nitekim bu elemanı $A_1$ ve $A_2$ noktalarını sabitlediğinden, bu noktalara komşu olan
$(0,0,0,0)$ ve $(1,1,0,0)$
noktalarını birbirine götürmek zorundadır. Ama $(0,0,0,0)$ noktasını zaten kendisine götürüyor, demek ki $(1,1,0,0)$ noktasını da kendine götürmek zorundadır. Bu fikri devam ettirirsek, $\sigma^{-1}$$\alpha^{-1}$$g$ elemanının $K$’nın tüm noktalarını sabitlediği, yani $Id_{16}$ olduğu anlaşılır. Demek ki
$\sigma^{-1}$$\alpha^{-1}$$g$$=$$Id_{16}$
ve
$g$$=$$\alpha$$\sigma$$\in$$RSTU$
Soru: Küpün köşelerini $01$-üçlüleri olarak gösterelim. $0$ koordinatını $1$’e, $1$ koordinatını da $0$’a dönüştüren simetri $G$$=$$RST$ grubunda nasıl yazılır?
Örnek 6. $n$ boyutlu küpü
$K_n$=$\{(\delta_{1},…,\delta_{n}):$ her $i$ için $\}$
olarak tanımlayabiliriz. Eğer küpü, küpün içini de içerecek biçimde tanımlamak istersek,
$K_n$=$\{(\delta_{1},…,\delta_{n}):$ her $i$ için $\delta_{i}\in \left [ 0,1 \right ]$$\}$
tanımını yapabiliriz. Bizim için hangi tanımın kabul edildiği farketmeyecek. Fikirleri sabitemek amacıyla birincisini kabul edelim. Eğer iki noktanın sadece
bir koordinatı değişikse, bu noktalar arasında bir bağlantı olsun. (Bağlantılar küpün kenarlarıdır.) $K_n$’nin $2n × n!$ tane simetrisi vardır. Bu, aynen yukarıdaki iki örnekteki yöntemle gösterilebilir. Ama bunların hepsi $n$ boyutlu uzayı eğip bükmeden gerçekleşmez, bazıları ayna simetrileridir. Sadece yarısı
$n$-boyutlu uzaydan çıkmadan gerçekleştirilebilir.
Örnek 7.
$\prod_{\omega }$$\{ 0,1 \}$ ve $\oplus _{\omega}$$\{0,1\}$kümelerinden de bir nevi sonsuz boyutlu küp elde edilebilir. İki köşenin (noktanın yani) bağlantılı olması demek, tek bir koordinatın farklı olması demektir. Bu küplerin de simetri grupları vardır. Ama bu sefer simetriyi biraz farklı tanımlamak gerekebilir. Daha önce simetriyi
$A$ ile $B$ köşeleri bağlantılıysa,
$f(A)$ ile $f(B)$ köşeleri de bağlantılıdır
koşulunu sağlayan köşelerin bir $f$ permütasyonu
olarak tanımlanmıştık. Bu sefer,
$A$ ile $B$ köşelerinin bağlantılı olması için
$f(A)$ ile $f(B)$ köşelerinin bağlantılı olmaları
yeter ve gerektir
koşulunu sağlayan köşelerin bir $f$ permütasyonu olarak tanımlamak gerekir, ki eğer $f$ bir simetriyse, $f^{-1}$ de bir simetri olsun. (Ama bu özelliğin sağlanması için eski tanım da yeterli olabilir. Bu cümleden de anlaşılacağı üzere sonsuz boyutlu küplerin simetri grubu hakkında bu yazarın bir bilgisi bulunmamaktadır.)
8. Oktahedronun Simetrileri. Oktahedron, aşağıdaki 6 köşeli, 12 kenarlı, 8 yüzeyli düzgün cisimdir.
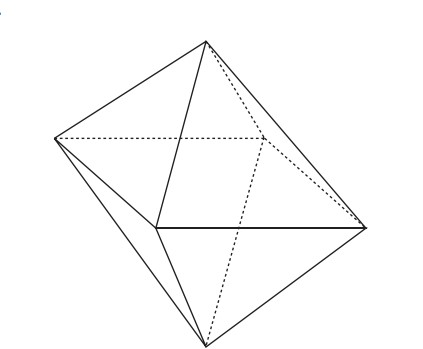
Küpün örneğinde olduğu gibi köşeleri değil de, yüzeyleri birbirine dönüştüren 8 elemanlı bir simetri grubu bulmak zor değildir. Mesela dikey eksen etrafında döndürülerle, yatay düzleme göre ayna simetrisi böyle bir grup verir. Bu grup sayesinde oktahedronun $8 × 3! = 48$ tane simetrisi olduğunu göstermek zor değildir. Okur alıştırma olarak bunu göstermelidir. Biz burada bir başka yöntem kullanacağız. Üç boyutlu küpün her yüzeyinin ağırlık noktasını alıp, komşu yüzeylerin ağırlık merkezlerini birleştirirsek bir oktahedron elde ederiz.
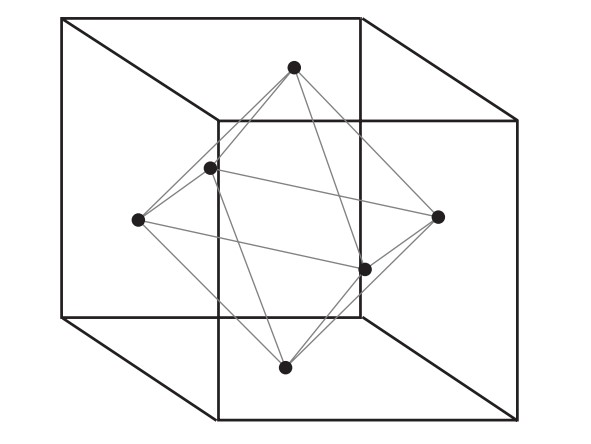
Bu sayede küpün her simetrisinin oktahedronun bir simetrisine yol açtığını gözlemleyebiliriz. Nitekim küpün bir $\sigma$ simetrisini ve bir $ABCD$ yüzeyini alalım. $\sigma$, mesafesi 2 olan $A$ ve $C$ köşelerini mesafesi 2 olan $\sigma(A)$ ve $\sigma(C)$ köşelerine götürür. Dolayısıyla $A$ ve $C$ köşelerinin ortak komşuları olan $B$ ve $C$ köşelerini $\sigma(A)$ ve $\sigma(B)$ köşelerinin ortak komşularına götürür. Demek ki $\sigma$ simetrisi küpün $ABCD$ yüzeyini gene küpün bir başka yüzeyine, $\sigma(A)\sigma(B)\sigma(C)\sigma(D)$ yüzeyine götürür. Dolayısıyla $\sigma$ simetrisi küpün $ABCD$ yüzeyinin orta noktasını $\sigma(A)\sigma(B)\sigma(C)\sigma(D)$ yüzeyinin orta noktasına götürür, yani küpün içine çizilen oktahedronu gene oktahedrona götürür.Nasıl küpten oktahedron elde etmişsek, oktahedrondan da benzer şekilde bir küp elde ederiz.
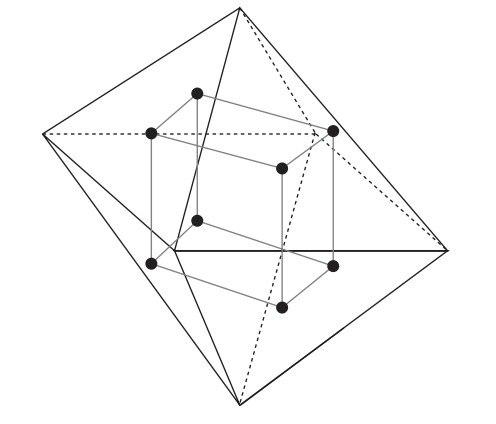
Aynen yukarıdaki yaptığımız gibi oktahedronun her simetrisinin küpün bir simetrisini verdiği kanıtlanabilir. Dolayısıyla oktahedronun simetri grubuyla 3 boyutlu küpün simetri grubu aynıdır.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 2013 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Emre Şahin‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz.

