Yazar: Doğan Dönmez (Çukurova Üniversitesi Matematik Bölümü öğretim üyesi)
Yıl: 1995-3
Sayı: 23
Pek çoğumuz canımız sıkıldığında, elimizde bir kalem, önümüzde de bir kağıt varsa, bu kağıda eğriler çizeriz. Gelin bu eğriler üzerine biraz düşünelim. Bu yazıda el kaldırılmadan çizilen ve başlangıç noktasına geri dönen (yani kapalı) eğrilerle ilgileneceğiz. Örneğin bir çember, kare veya daha karmaşık bir şey, sonsuz sembolü gibi olabilir bu eğri.
Biz bu eğrinin kendisiyle değil de, düzlemin eğri üzerinde olmayan noktalarının kümesiyle (yani eğrinin noktalarının düzlemdeki tümleyeni ile) ilgileneceğiz. Bu kümelerin pek fazla ortak yönü yok gibi görünse de aşağıdaki iki özelliğin her örnekte var olduğunu görebilirsiniz. (Burada, eğrimizin bir parçası üzerinde birden fazla defa geçilmediğini de varsayıyoruz.)
- Bu küme tek parça değildir; iki veya daha fazla parçadan oluşur.
- Bu parçalardan yalnızca bir tanesi sınırsız, diğerleri sınırlıdır.
Kısacası, kapalı bir eğri düzlemi parçalara ayırır, bu parçalardan biri sınırsız diğerleri sınırlıdır. Burada parça, sınırlı, sınırsız sözcüklerinin tam matematiksel tanımını okuyanlara bırakalım. Dikkatli bir okuyucu yukarıdaki kapalı eğri tanımının yetersiz olduğunu (çünkü kalem, elimizi kaldırmadan gibi kavramlara dayanıyor) farkedecektir, matematiksel bir tanım, süreklilik kavramı kullanılarak yapılabilir.
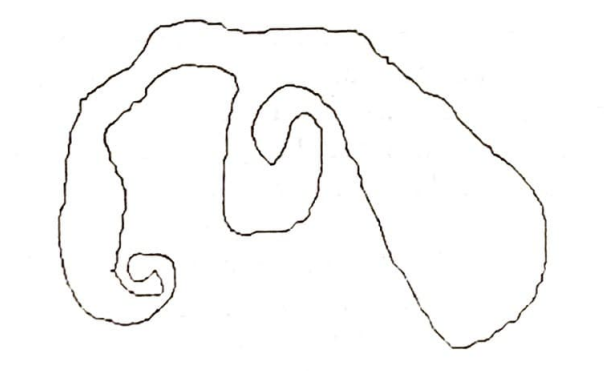
Bu sonucu daha basitleştirmek ve başka yüzeylere de genelleştirebilmek için, kapalı eğrimizi üzerine bir koşul daha ekleyerek biraz daha özel seçeceğiz. Kalemimizin, aynı nokta üzerinden tekrar geçmemesi koşulu eğrimizi, basit kapalı eğri diye adlandırılan eğri yapar. Basit kapalı bir eğri için yukarıdaki iki gözlem Şekil 1’deki şekile dönüşür.
Basit kapalı bir eğri, düzlemi, biri sınırlı (eğrinin içi), diğeri sınırsız (eğrinin dışı) iki parçaya ayırır. (Düzlemin bu özelliği sayesinde, kümeleri Venn şemaları ile gösterebiliyoruz!).
Yukarıdaki gözlem apaçık görünse bile (en azından matematikçiler için) kanıtlanması gerekir. Bu da (ve biraz daha fazlası) ünlü Jordan Eğri Teoremi ile kanıtlanmıştır:
Jordan Eğri Teoremi 1. Basit kapalı bir eğri, düzlemi, biri sınırlı, diğeri sınırsız iki parçaya ayırır ve eğrinin her noktasına her iki parçadan da istenildiği kadar yaklaşılabilir.
Biz bu teoremin yalnızca ilk kısmı ile ilgileneceğiz. Bu neredeyse aşikâr görünen teoremin kanıtı hiç de kolay değildir; örneğin [2]’de verilen kanıt tam dokuz sayfa uzunluğundadır.
Başka yüzeyler için aynı sorunun cevabını aramadan önce ayırma konusuna başka bir açıdan da bakabileceğimizi belirtelim. Düzlemi ayırmanın önemi, belli koşulları sağlayan eğrilerin kesişeceği sonucunu vermesindedir. Örneğin teoremdeki bu iki parçanın birinden başlayıp diğerinde sona eren (el kaldırmadan çizilen!) bir eğri ilk çizdiğimiz eğriyi kesmek zorunda kalır (parçalara ayırmanın matematiksel tanımı bu olacaktır). Kesişmeyle ilgili şu problemi düşünelim:
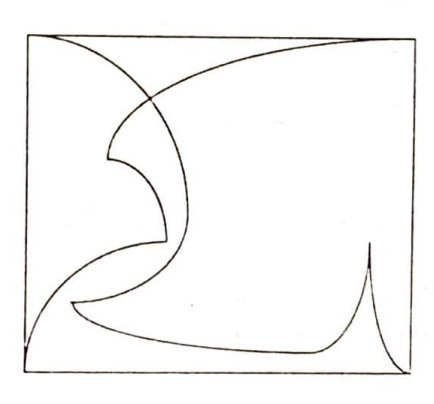
Bir dikdörtgenin karşılıklı köşelerini birleştiren eğrilerin (eğriler el kaldırılmadan çizilmek ve dikdörtgenin içinde kalmak koşuluyla) mutlaka kesiştiğini gösterin (Şekil 2). Bu “apaçık” gerçek de, kanıtlanması pek de kolay olmayan bir önermedir ve “elemanter” bir kanıtı, Jordan eğri teoremi yardımıyla yapılabilir.
([1]’deki ödüllü bulmaca da bunun gösterilmesine dönüşür, fakat oradaki eğriler daha özel (fonksiyon grafiği) olduklarından şok daha basit bir kanıt da vardır.)
Şimdi basit kapalı bir eğrinin (dikkat edilirse bu tanım noktalar bir yüzey üzerinde olduğunda da anlamlıdır) başka yüzeyleri de ayırıp ayırmadığı sorusu üzerinde biraz düşünelim.
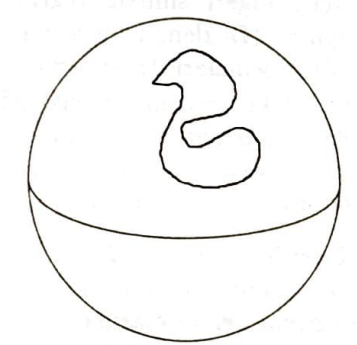
Yüzey olarak küreyi göz önüne aldığımızda da (Şekil 3) aynı sonuca varıyoruz, yani
Jordan Eğri Teoremi 2. Küre üzerindeki basit kapalı bir eğri küreyi iki parçaya ayırır.
Bu teoremlerin ikisine de Jordan Eğri Teoremi adı verilir, bunun nedeni, bunlardan birinden diğerinin kanıtının kolayca yapılabilmesidir. Bunun için de, kürenin bir noktası çıkarılınca kalan kümenin düzlemle “aynı” olduğu gözlemi kullanılır. Yani düzlemdeki ayırma özelliği küre için de geçerli; fakat bunun başka yüzeylerde doğru olmadığını birazdan göreceğiz.
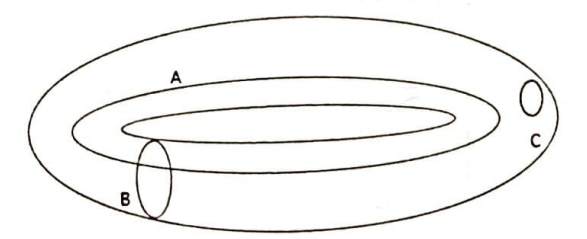
Şimdi uzaydaki başka bir yüzeyi gözönüne alalım. Torus (veya tor) denen yüzey bir otomobil iç lastiği şeklindedir (Şekil 4).
Bu yüzeyde Jordan Eğri Teoremi (biraz önce yazdığımız şekliyle) yanlıştır. Şekil 4’teki $A$ eğrisi basit kapalı bir eğri olduğu halde torusu ayırmaz; aynı şey $B$ eğrisi için de geçerlidir: fakat $C$ eğrisi, aynen düzlem ve kürede olduğu yüzeyi ayırır. Yani bazı basit kapalı eğriler torusu ayırıyor, bazıları ayırmıyor. Şimdi matematikçinin aklına doğal olarak şu soru gelecektir: “Hangi basit kapalı eğriler torus yüzeyini ayırır?” Yanıtı pek kolay olmayan bir soru bu. Yanıtını vermeden önce yeni bir kavram tanımlayacağız: (bir noktaya) büzülebilme. Matematiksel açıdan tam olmayan ama temel fikri veren tanımı şöyle yapılabilir: Basit kapalı bir eğri, eğer yavaş yavaş, fakat üzerinde bulunduğu yüzeyin dışına çıkmadan ve eğriyi koparmadan, bir noktaya büzülebiliyorsa ona (o yüzeyde) büzülebilen eğri denir. (Dikkat: büzülebilir olup olmamak, eğrinin içinde bulunduğu yüzeye bağlı!). Bunların örneklerini kolayca bulabiliriz: düzlemdeki ve küredeki her kapalı eğri büzülebilirdir ve torus üzerindeki $C$ eğrisi büzülebilir eğrilerdir ama $A$ ve $B$ eğrileri (torus üzerinde!) büzülemez eğrilerdir. Bu örneklerle Jordan Eğri Teoremi’ni karşılaştırdığımızda, Jordan Eğri Teoremi’nin hem düzlem hem küre hem de torus için nasıl genelleştirileceğini tahmin edebilirsiniz.
Jordan Eğri Teoremi 3. Düzlem, küre veya torus üzerindeki basit kapalı bir eğrinin, o yüzeyi iki parçaya ayırabilmesi için gerek ve yeter koşul o eğrinin (o yüzey üzerinde) büzülebilir olmasıdır.
(Dikkat: bu sonuç uzaydaki her yüzey için geçerli değildir; örneğin silindir üzerinde çizili olan çember büzülemez fakat silindiri ayırır.)
Jordan Eğri Teoremi’ni başka yüzeylere de, büzülebilirlikten biraz daha karmaşık bir kavram kullanarak genişletilebiliriz. Düzlem, küre ve torus için bu iki kavramın çakışması nedeniyle bu yüzeylerde Jordan Eğri Teoremi’nin ifadesi daha basittir.
Jordan Eğri Teoremi’nin ifadesi ve kanıtı pek çok kitapta bulunduğu ve bu kitaplar torus için olanın kanıtında gereken her tekniği içermesine rağmen ben bu şekilde ifadesini ve kanıtını henüz bir yerde görmedim.
Bu gibi sonuçlar, matematiğin Cebirsel Topoloji olarak adlandırılan dalında kullanılan tekniklerle kanıtlanır. 19. yüzyıl sonlarında şekillenip şok hızlı bir şekilde gelişen ve geometri ve analizde pek çok problemin çözümünde önemli rol oynayan, aynı zamanda matematiğin diğer dalların da etkileyen Cebirsel Topoloji’nin matematikle ilgilenenlere zevk ve heyecan vereceğine eminim.
KAYNAKÇA
[1] B. Güvenç, Ödüllü Problem, Matematik Dünyası, 2, sayı 2, 21 (1992).
[2] C. Uluçay, Konform Tasvir, Şirketi Mürettibiye, Istanbul, 1955.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 3. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Atahan Haznedar‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

