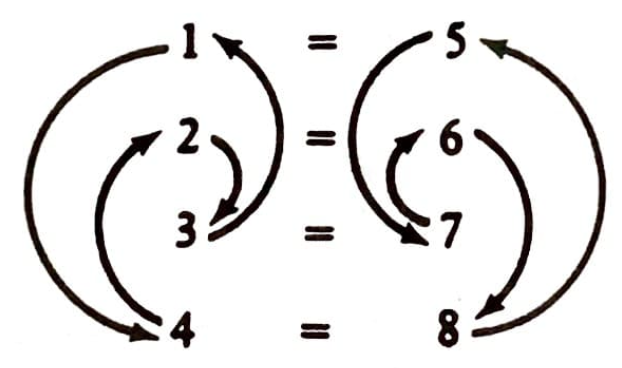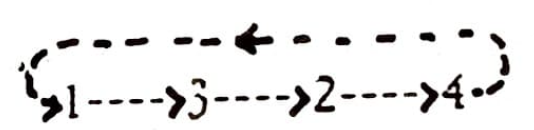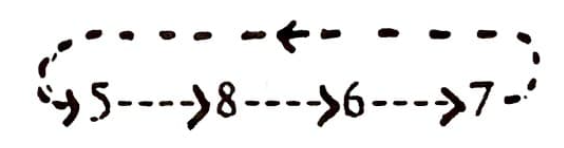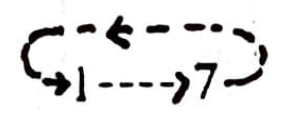Evliliğin Mantığı Olur Mu?

Yazar: Asuman Güven Aksoy (Claremont McKenna College Matematik Bölümü öğretim üyesi)

Yıl: 1995-2

Sayı: 22

Avusturalya’nın yerlileri evlilik ve akrabalık ilişkilerine getirdikleri kurallarla meşhurdur. Bunlardan Warlpiri denen bir grup yerlinin özellikle karmaşık bir akrabalık sitemi vardır. Warlpiriler Avusturalya’nın kuzeyindeki çöllük bölgede yaşıyorlar. Akrabalık ilişkilerinde izledikleri kurallar dizgesi onların toplumsal, politik organizasyonlarını ve tavırlarını bütünüyle tanımlıyor, sosyal çevredeki herkesi içeriyor ve felsefi dünyalarına kadar uzanıyor.

Avusturalya yerlileri göçebedir ve avcılıkla geçinir. Yiyecek ve suyun kolayca bulunabileceği bölgelerde yaşarlar, 10 ile 60 kişilik gruplar halinde gezinirler ama bazı özel durumlarda bağlantılı grupların hepsi bir araya gelir. Kişisel varlık yönünden yoksul olsalar da toplumsal ve duygusal dünyaları zengin ve gizemlidir.

Warlpiri akrabalık sisteminin 8 bölümü vardır. Her bölümde hem kadın hem erkek vardır ve herkes bu sekiz bölümden birine girmek zorundadır. Evlenecek insanlar ayrı ayrı bölümlerden gelmek zorundadır. Aşağıda örneklerle açıklayacağımız gibi doğan çocukların anne ve babalarından farklı, annenin belirleyeceği bir bölüme girmesi zorunludur. Basitçe bölümleri 1,2, …, 8 diye numaralayalım. Aşağıdaki şema evlilik kurallarını gösteriyor.

Eşitlik (“=”) evlilik anlamında; her ok da annenin bölümünden çocuğun bölümüne yönlendirilmiş. Örneğin, 1. bölümdeki erkek 5. bölümdeki bir kadınla evleniyor ve çocukları da 7. bölüme giriyor (7. bölüm 5. ile aynı sütunda). Bir başka örneği ele alalım; diyelim ki 6. bölümdeki bir erkek 2. bölümden bir kadınla evleniyor ve onların çocukları da 3. bölümde (3. bölüm 2. ile aynı sütunda). Sonuç cinsiyete göre değiştiğinden önce bir kadından başlayıp birkaç kuşak gerideki annelere bakalım. 1. bölümdeki bir kadının annesi 3 . bölümde, onun annesi de (yani 1. bölümdeki kadının anneannesi) 2. ve onun annesi de (büyükannesi) 4. bölümde. 4. bölümdeki kadının annesi de tekrar 1. bölümde yer alıyor. Aşağıdaki şema birkaç kuşak “anneler devresi”ni (anne/kız) gösteriyor:

Aynı model, nereden başlarsanız başlayın tekrarlıyor kendini. Benzer biçimde aşağıda bir başka anneler devresinin şeması var:

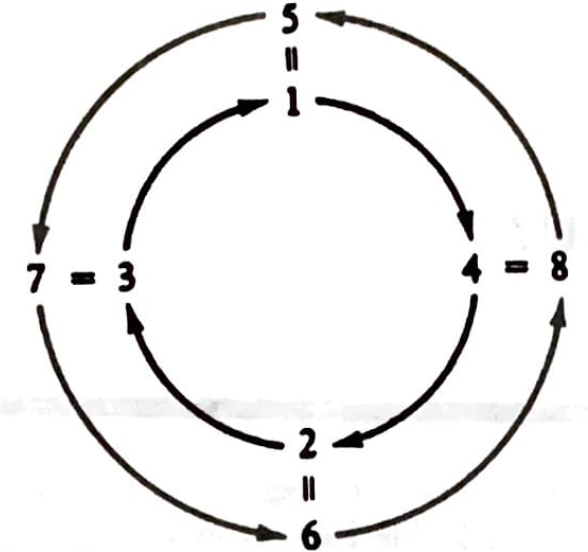
Devreler üst üste çakışmadığından her devre 8’in yarısı kadar bölüm gösterecektir. Antropologlar bu 4 bölümden oluşan gruba “yarım hisse” diye isim bile vermişlerdir. Aşağıdaki şema evlilik kurallarını ve anneler devresini bir kez daha açıklamaktadır:

“=” evlilik anlamında kullanılmış olup, oklar annenin bölümünden çocuğa yönlendirilmiştir.

Şimdi baba ve oğullara ne olduğuna bakalım. 1. bölümdeki bir erkek 5 . bölümden bir kadınla evleniyor, oğulları da 7. bölümde. Bu oğul 3. bölümden bir kadınla evleniyor, onların oğulları da 1. bölümde. Görülüyor ki “babalar devresi”nin (baba/oğul) uzunluğu 2:

Benzer biçimde diğer baba/oğul devreleri (2,8), (3,6), ve (4,5). Miras hakları, toprak paylaşmaları, hatta dini törenler bile bu gruplara göre yapılıyor.

Anne/kız ve baba/oğul devreleri Warlpiriler’in akrabalık sisteminin temelini oluşturuyor ve Avustralya yerlilerinin dünya felsefelerini yansıtıyor. Geçmiş ve geleceği yaşadıkları ana güzelce bağlıyorlar.
Aşağıda öbek dilinde açıklayacağımız gibi, Warlpiriler’in evliliklerinin bir mantığı var. Bu sisteme matematik dilinde 8. mertebeden ikidüzlemli (dihedral) öbek denebilir. 1. bölüme $I$ (özdeşlik) diyelim. $I$’daki herkesin annesi 3. bölümde olduğundan, 3. bölümü $a$ (anne) ile isimlendirelim. 3. bölümdeki herkesin annesi 2. bölümdedir. Bu nedenle 2. bölümü $aa$ (anneanne) ile isimlendirelim. Bu durumda 4. bölüm $aaa$ (anneannenin annesi) oluyor. Benzer biçimde $b$ ile babaları ifade edersek, 7. bölümdekilerin babaları $I$’da olduğundan 7’ye $b$ dersek, 5, 8 ve 6 , sırayla $ab,aab$ ve $aaab$ oluyor. Harflerin düzeni önemli burada. Mesela $ab$ ile $I$ grubundaki babaların annelerini kastediyoruz. Bunlar annelerin babalarından farklı.

Yazılanları kısaltmak için örneğin $aaa$ yerine $a^3$ kullanacağız. Bu nedenle 8 bölümü

$$\begin{array}{cccccccc}1& 2& 3& 4& 5& 6& 7& 8\\ 1& a^2& a& a^3& ab& a^{3}b& b& a^{2}b\end{array}$$ ile göstereceğiz. Sözgelimi, $ab$ bölümündeki insanların annelerinin bölümünü arıyorsak, $a(ab)=a^{2}b$’ye geliyoruz. Gelgelelim, bazı durumlarda bu pek kolay değil. Örneğin, $ab$’deki insanların babaları $a^3$’te yer alıyor; yani $b(ab)=a^3$. Aşağıdaki tabloda olabilecek bütün eşleştirmeler gösterilmiştir. Sütun başlıkları çiftin ilkini, sıralar da uygulanan ilişkiyi temsil ediyor. Yukarıdaki örneklere dönersek, $a^{2}b$, $ab$ ile başlayan sütunla $a$ ile temsil edilen sıranın kesiştiği yerdedir. Öte yandan $a^3$, $ab$ sütunu ve $b$’li sıranın kesiştiği yerde oluyor.

$$\begin{array}{ccccccccc}& I& a& a^2& a^3& b& ab& a^{2}b& a^{3}b\\ I& I& a& a^2& a^3& b& ab& a^{2}b& a^{3}b\\ a& a& a^2& a^3& I& ab& a^{2}b& a^{3}b& b\\ a^2& a^2& a^3& I& a& a^{2}b& a^{3}b& b& ab\\ a^3& a^3& I& a& a^2& a^{3}b& b& ab& a^{2}b\\ b& b& a^{3}b& a^{2}b& ab& I& a^3& a^2& a\\ ab& ab& b& a^{3}b& a^{2}b& a& I& a^3& a^2\\ a^{2}b& a^{2}b& ab& b& a^{3}b& a^2& a& I& a^3\\ a^{3}b& a^{3}b& a^{2}b& ab& b& a^3& a^2& a& I\end{array}$$

Yukarıdaki tablonun en önemli özelliği, olabilecek bütün eşleştirmelerin bu ilk sekizli bölümden birinde sonuçlanmasıdır. Bu durumu açıklayan matematiksel bir terim vardır. Bu özelliğe kapalılık denir. $I$ ile başlayan sütun ve sırada her şeyin kendini tekrar ettiğinin farkında mısınız? Dolayısıyla $I$ özdeşlik elemanı. Tablonun bir başka önemli özelliği ise $I$’nın her sütun ve sırada bir kere ortaya çıkması. Dolayısıyla bir başka özellik, ters öğenin olması her bölümü $I$’ya geri bağlayan. Örneğin $a^3$, $a$’nın ters öğesi, $a^{3}b$ kendisinin ters öğesi. Şimdiye kadar bu bölümlerin üç özelliğinden bahsettik: kapalılık, özdeşlik ve ters öge. Bunlardan başka bir de birleşme özelliği varsa, matematikçilerin öbek dediği yapıyı görüyoruz. Birleşme özelliğinin anlamı ardarda uygulanan ilişkilerde önceliğin bir şey farkettirmeden aynı sonucu vermesi demektir. Örneğin,

$$aab=a(ab)=(aa)b=a^{2}b.$$

Yukarıda sözü edilen bu belirleyici özelliklerden dolayı öbekteki her öğe yalnızca bir kez her sütun ve sırada ortaya çıkmakta. Bu nedenle, Warlpirili her insan bu 8 bölümden birindedir. Her bölümün, diğer her bölümle bir akrabalık ilişkisi vardır. Aşağıdaki üç özellik bu öbeği diğer öbeklerden ayırarak 8 düzenli ikidüzlemli öbek yapmaktadır. Bu özellikler şunlardır:

$$a^4=I,b^2=I\text{ ve }(ab)(ba)=I.$$

Bunlardan ilki “anneler devresi,” ikincisi “babalar devresi,” son özellik ise “evlilik kuralı.” Matematiksel dilde, $a$ ve $b$ ikidüzlemli öbeğin üreteçleri ve

$$a^4=I,b^2=I\text{ ve }(ab)(ab)=I$$

öbeğin tanımını veren özellikler. Hangi bölümün $I$ ile isimlendirilmesi ise bu mantıksal yapıyı tanımlayan ilişkileri hiç değiştirmiyor.

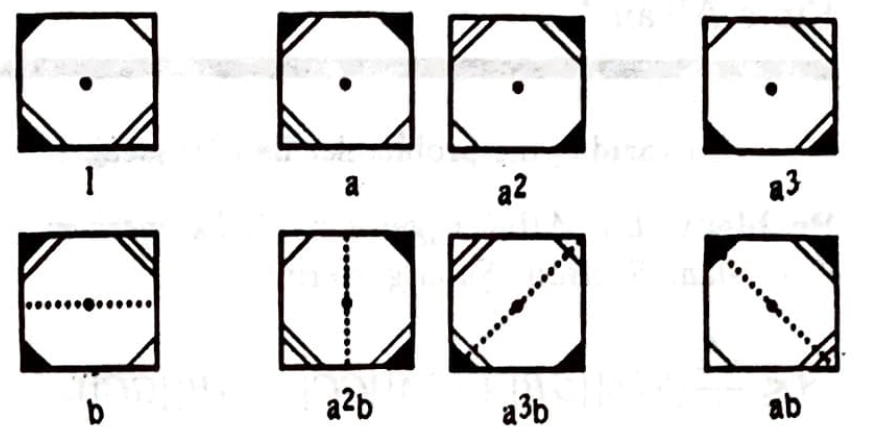
İkidüzlemli öbek kavramı aynı mantığı içeren geometrik bir modelden gelmektedir. Karenin simetrileri ile Warlpiriler’in akrabalık sistemleri birbirinin aynısı. Şöyle ki, eğer bir kareyi, merkezi etrafında 90 derece döndürürseniz, sonuç yine bir karedir ama köşelerinin yerleri değişmiştir. Benzer biçimde 180 ve 270 derece çevirmek köşelerin yerlerini değiştirir ama yine elinizde kare vardır. Karenin merkezinden geçen yatay ve dikey doğruları veya karenin köşegenlerini düşünün. Kareyi bu doğrulara göre yansıtırsanız, yine kare elde edersiniz. Bu yansıtma ve döndürmeleri istediğiniz sırada uygulayın; aşağıdaki şemada görülen 8 olasılıktan başka bir sonuç alamayacaksınız. Köşelerin değişik şekilde işaretlenmesi her haraketten sonraki yerlerini göstermektedir. Herhangi bir pozisyonu $I$ ile işaretlersek, merkez etrafında 90 derece döndürmeye $a$, merkezden geçen yatay doğruya göre yansıtmaya da $b$ dersek, diğer pozisyonlar $a$ ile $b$’nin kombinasyonu biçiminde ortaya çıkacaktır. 4 kez 90 derece döndürürseniz ilk pozisyona geri gelirsiniz, yani $a^4=I$. İki kez yatay doğruya göre yansıtırsanız yine ilk pozisyona gelirsiniz, yani $b^2=I$. İki kez köşegenden geçen doğruya göre yansıtırsanız yine ilk duruma gelirsiniz, bu da $(ab)(ab)=I$’ya karşılıktır .

İşte yine $a^4=I$, $b^2=I$ ve $(ab)(ab)=I$’yı bulduk, yani ikidüzlemli öbeği tanımlayan özellikleri. Hiç birbiriyle ilgili gibi gözükmeyen, karenin 8 simetrisi ile Warlpiriler’in akrabalık sisteminin 8 kısmı, aynı özelliklerle tanımlanmaktadır.

Doğal olarak, Warlpirili biri evliliğin bu analizini yapmaz, herkes hangi bölümde olacağını, bölümün getirdiği sorumlulukları bilip tavrını ve kurallarını ona göre ayarlar. Bu topluluğun geçmişteki, şimdiki ve gelecekteki her üyesi, topluluğun diğer bütün üyeleri ile bağlantılıdır. Bu sistemin mantığı bizim bildiğimiz akrabalık ilişkileri kapsamında değerlendirilemez; senin akraban, benim akrabam, yakın akraba, uzak akraba kavramları bu sistemde çalışmaz. Warlpiriler’in yaşadıkları zamandaki sorumlulukları ve davranışları hem geçmişe hem geleceğe uzanmaktadır.

Kaynakça

[1] M. Ascher, Ethnomathematics: The Multicultural View of Mathematical Ideas, Cole, 1991.

[2] M. Laughren, Warlpiri Kinship Structure, Languages of Kinship in Aboriginal Australia, University of Sydney, 1982.

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.