Yazar: Hasan Gökpınar (Gaziantep Üniversitesi, Matematik Bölümü)

Yıl: 1995-1

Sayı: 21

Özet

I cetveli ile, aralarındaki uzaklık cetvel genişliği kadar olan iki paralel doğru, belirli bir noktadan belirli bir doğruya dik ya da paralel doğru ve belirli bir açının ortayı çizilebilir. Buna göre, cetvel genişliği $l$ ile gösterilmek üzere, kenar uzunlukları $l$, $\sqrt{3}$, $2$, ve $l$, $\sqrt{5+2\sqrt{5}}$, $1+ \sqrt{5}$ olan dik üçgenler çizildiğinde aşağıdaki şekilde ölçüleri gösterilmiş olan açılar elde edilir.

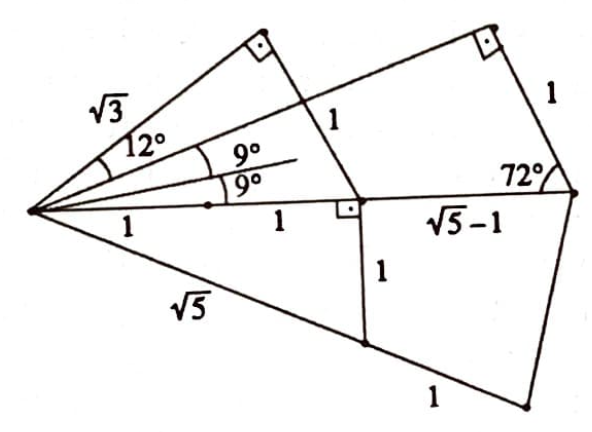
Ayrıntılar

I cetveli ile yapabilecek bazı çizimler ve açıklamaları:

$\quad$(1) İşaretlenmiş iki noktadan geçen bir doğru çizmek.

$\quad$(2) Aralarındaki uzaklık cetvel genişliğinden daha büyük olan iki nokta işaretlendiğinde, herbiri bu noktaların birinden geçen ve aralarındaki uzaklık cetvel genişliği kadar olan iki paralel doğru çizmek.

$\quad$(3) Bir eşkenar dörtgen çizmek.

$\quad$(4) Belirli bir nokatadan belirli bir doğruya paralel doğru çizmek.

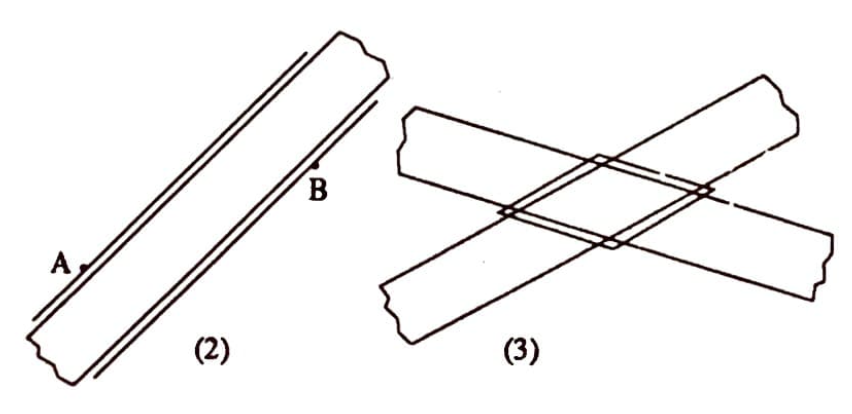
Açıklama: Verilen bir $A$ noktasından verilen bir $d$ doğrusuna paralel çizmek için, önce $d$ doğrusu üzerinde rasgele bir $B$ noktası alınır. $A$ ve $B$ noktaları için (2) deki çizim iki değişik konumda yapıldığında (3) deki eşkenar dörtgen elde edilir. Sonra, bu eşkenar dörtgenin bir kenarı yeterince uzatılakar $d$’yi kestiği $C$ noktası işaretlenir.

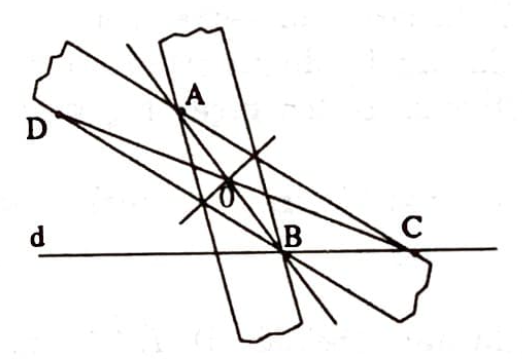
Karşılıklı iki köşesi $A$, $B$ olan eşkenar dörtgenin, birbirini dik olarak ortalayan köşegenlerinin kesim noktası, $O$, $C$ ile birleştirilirse $CO$ doğrusunun $B$ köşesinden geçen kenarı kestiği $D$ noktası, $A$’dan geçen ve $d$’ye paralel olan doğrunun bir noktası olur. $AD\, ||\, d$’dir.

$\quad$(5) Belirli bir noktadan belirli bir doğruya dik çizmek.

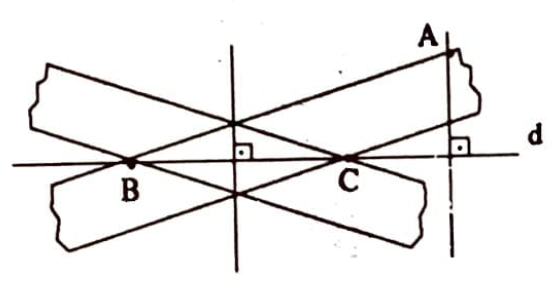
Açıklama: Verilen bir $A$ noktasından verilen bir $d$ doğrusuna dik çizmek için, önce $d$ doğrusu üzerinde rasgele bir $B$ noktası alınır. Sonra, cetvelin bir kenarı ile $AB$ doğrusu çizilirken diğer kenarın $d$’yi kestiği $C$ noktası işaretlenir. $B$ ve $C$ noktaları için (2) deki çizim yapıldığında bir köşegeni $BC$ olan bir eşkenar dörtgen elde edilir ki bu eşkenar dörtgenin diğer köşegeni $d$’ye diktir. Bu köşegene $A$’dan paralel çizilirse $A$’dan $d$’ye dik çizilmiş olur.

$\quad$(6) Belirli bir açının ortayını çizmek.

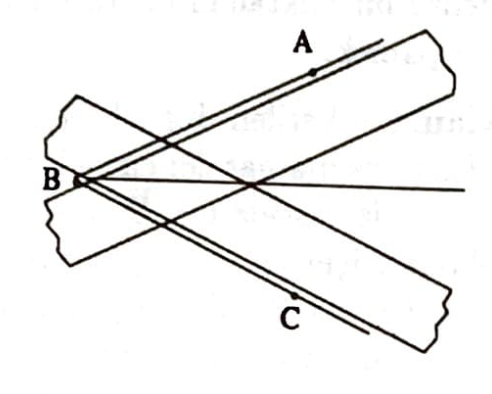
Açıklama: Verilen açı $\widehat{A B C}$ olsun. $AB$ ve $CB$ kenarlarına cetvel genişliği kadar uzaklıktan iki paralel doğru çizilirse elde edilen eşkenar dörtgenin $B$’den geçen köşegeni $\widehat{B}$’nin ortayı olur.

$\quad$(7) İki açıyı birbirine eklemek ya da birbirinden çıkarmak.

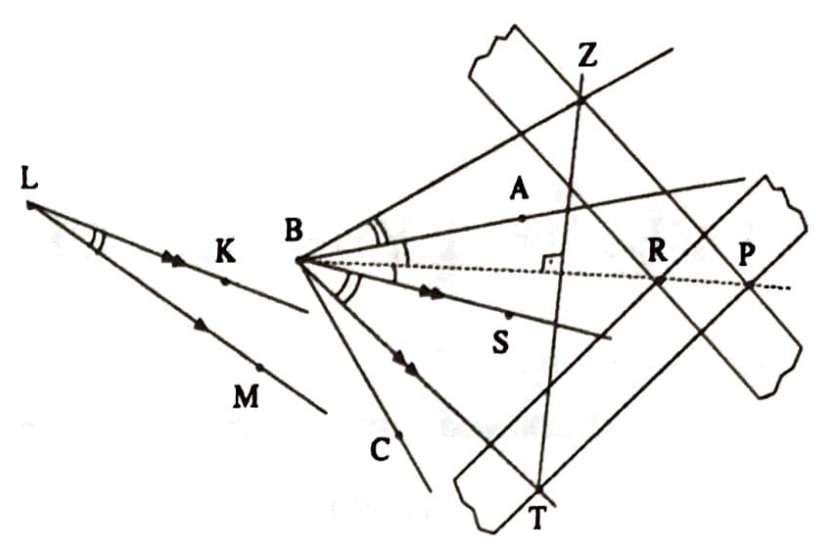
Açıklama: (Şekildeki) $\widehat{K L M}$’nı $\widehat{A B C}$ üzerine eklemek için önce $B$’den $K L$ ve $M L$’ye paraleller çizilerek $\widehat{K L M}$’na eş $\widehat{S B T}$ elde edilir. Ayrıca $\widehat{A B S}$’nın ortayı çizilir. Sonra, bu açıortay üzerinde rasgele bir $P$ noktası alınıp $T$ ile birleştirilirken, cetvelin diğer kenarı ile $P T$’ye bir paralel çizilir. Bu paralelin açırtayı kestiği $R$ noktası işaretlenir. $P$ ve $R$ noktaları için (2) daki çizim yapılır. $T$’den açıortaya çizilen dikme ile $P$’den geşen doğrunun kesiştiği $Z$ noktası $B$’ye birleştirilirse $\widehat{Z B A}=\widehat{S B T}=\widehat{K L M}$ ve $\widehat{Z B C}=\widehat{A B C}+\widehat{K L M}$ olur.

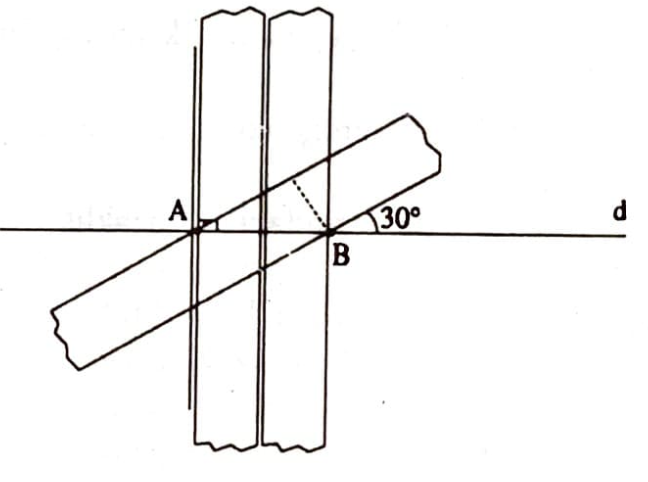
Bu çizimler birlikte gözönüne alınarak, kenar uzunlukları $1,2,3,4,5, \ldots$ ve/veya $\sqrt{2},\sqrt{3}, \sqrt{5}, \sqrt{6}, \ldots$ olan dik üçgenler ve dolayısıyla trigonometrik oranları bilinen birçok açı çizilebilir. Örneğin; hipotenüsü $2$ birim ve bir dik kenarı $1$ birim olan $30^{\circ}, 60^{\circ}, 90^{\circ}$ dik üçgeni şöyle çizilir:

Bir $d$ doğrusu üzerinde bir $A$ noktası işaretlenir. $A$’dan $d$’ye dik çizilir. Bu dikmeye cetvel genişliği kadar uzaklıkta bir paralel ve bu paralele gene cetvel genişliği kadar uzaklıkta bir paralel ve bu paralele gene cetvel genişliği kadar uzaklıkta ikinci bir paralel çizilerek $d$’yi kestiği $B$ noktası bulunur. $A$ ve $B$’ye (2) deki çizim uygulanırsa, yani cetveli $A$ ve $B$ arasına getirip biri $A$’dan diğeri $B$’den geçecek biçimde ve aralarındaki uzaklık cetvel genişliği kadar olan iki paralel doğru çizilirse $30^{\circ}$’lik açı elde edilir. $A$’dan veya $B$’den bu iki paralele dik çizilirse $30^{\circ}, 60^{\circ}, 90^{\circ}$ dik üçgeni elde edilir

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1995 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Atahan Haznedar‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.