Yazar: Mehmet Suat Bergil (Lefke Üniversitesi, ILCS)
Yıl: 1994-2
Antik çağın ünlü problemlerinden biri [1] dairenin geometrik yöntemle kare haline getirilmesiydi: sadece derecesiz bir cetvel ile pergel kullanmak suretiyle, belirli bir dairenin alanına eşit değerde alana sahip bir kare çizmek. Böyle bir çözümün olanaksızlığı 1882 yılında kanıtlandı [2].
Bu problemin kısmi ve/veya yaklaşık çözümleri üzerinde çalışıldığı da bir gerçektir. Getirdiği ilginç önerilerle Arşimet’ten 17. yüzyılda gerçekten de çarpıcı bir yaklaşım bulan Polonyalı keşiş Kochansky’ye kadar [3].
Yaklaşık Çözüm. Geometrik yöntemle dairenin kare haline getirilmesinde, $\varphi$ ile $\pi$ arasında saptanan bir bağlantı, kuramsal olarak (çizim sırasında oluşacak sapmalar dikkate alınmaksızın) % 99.9 oranında yaklaşık sonuç veren bir yöntem sunulacaktır.
Altın Oran ya da $\varphi$, kenarları 1 : 2 oranında olan dik açılı bir üçgende, kısa kenar ile hipotenüsün toplamının uzun kenara olan oranıyla belirlenen, $(1+\sqrt{5})/2$ değeridir [4].
Problemin Çözümü.
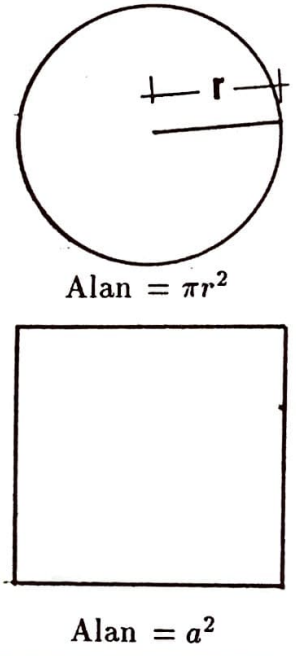
$\pi r^2 = a^2$ olması için $a=\sqrt{\pi} r $ olmalıdır. $\pi$ ile $\varphi$ arasındaki bağlantı:
$$\sqrt{\varphi} + \frac{1}{2} \simeq \sqrt{\pi}\ .$$
Kabul. % 0.1 oranında bir yanılma ile, $\sqrt{\varphi} +1/2 = \sqrt{\pi}$ kabul edelim.
$\sqrt{\pi} = \sqrt{\varphi} +1/2$ dediğimizde, $$a = \left(\sqrt{\varphi} + \frac{1}{2} \right)r = r\sqrt{\varphi} + \frac{r}{2}$$ olmalıdır. Öte yandan, bir uzunluğun $\sqrt{\varphi}$ değerini bulmak için uygulanan geometrik yöntem: Uzunluk gene $r$ olsun.
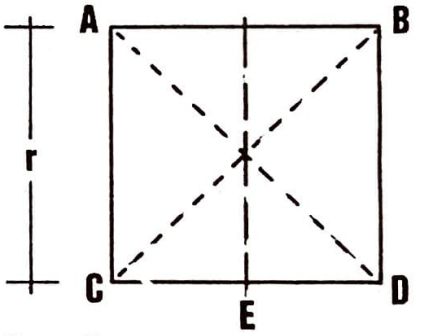
(I) Kenarı $r$ değerinde olan bir kare çizeriz ve $CD$’nin orta noktasına $E$ deriz.
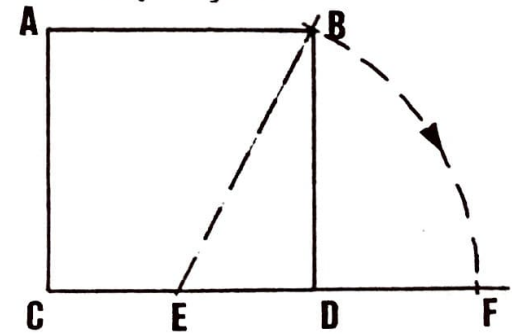
(II) Pergelimizi $E$’ye koyup $B$’yi $CD$’nin uzantısındaki $F$’ye taşırız.
(III) $AC$’yi kısa kenar, $CD$’yi de uzun kenar olarak alıp dikdörtgen çizersek kenarları 1 : $\varphi$ oranında olan $AGCF$ dikdörtgenini elde ederiz.
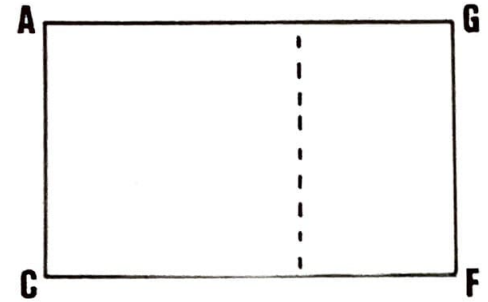
(IV) Şimdi de pergelimizi $C$’ye koyup $F$’yi $AG$’ye taşıyalım. Elde edeceğimiz $AH$ uzunluğu, $AC$’ye, yani $r$ uzunluğuna göre $r\sqrt{\varphi}$ değerini verecektir.
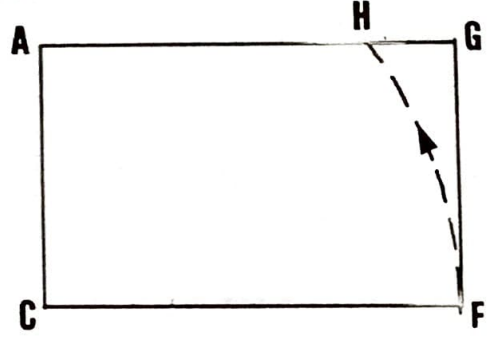
Formülümüzü bir daha hatırlayalım: $a = r \sqrt{\varphi} +r/2$. $r/2$’yi adım (I)’de zaten bulmuştuk. ($=CE$). $r\sqrt{\varphi}$’yi de adım (IV)’te bulduk ($=AH$).
O halde, $CE$ ve $AH$ uzunluklarını bir çizgi üzerine taşır da bu ($CE + AH$) uzunluğunu kenar olarak alıp bir kare çizersek, bu karenin alanı (kuramsal olarak) % 99.9 oranında, başlangıçtaki dairenin alanına eşit olacaktır.
KAYNAKÇA
[1] W. Gellert, et. al., editör, The VNR Concise Encyclopedia of Mathematics, Van Nostrand-Reinhold, New York, 1989.
[2] E.J. Borowski & Borwein, Dictionary of Mathematics, Collins, London, 1989.
[3] J.H. Cadwell, Topics in Recreational Mathematics, Cambridge University Press, Cambridge, 1966.
[4] M.S. Bergil, Doğada/Bilimde/Sanatta Altın Oran, Arkeoloji Sanat Yayınları, İstanbul, 1988.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1994 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

