Yazar: Hüseyin Demir
Yıl: 1993
Sayı: 11
Dörtgenler, üçgenden sonra işlenen çokgenlerdir. Batı dillerinde, üçgenler üzerine birçok kitap ve sayıları 10000’e yakın makale yazılmıştır. Dörtgenler üzerinde de pek çok araştırma yapılarak çok ilginç özellikler elde edilmiştir. Biz bunlardan bazılarına değinmekle yetineceğiz. Uzay dörtgenlerini (aykırı dörtgenleri) konumuzun dışında bırakıyoruz.
Sınıflama
Herhangi üç doğrusal olmayan $A$, $B$, $C$, $D$ gibi sıralı dört nokta verildiğinde $[AB]$, $[BC]$, $[CD]$, $[DA]$ doğru parçalarının birleşimine dörtgen deniliyor. $A$, $B$, $C$, $D$ noktalarına köşeler, bu doğru parçalarına kenarlar deniyor.
Köşelerin alınışına göre dörtgenler basit ve basit olmayan dörtgenler olarak iki sınıfa ayrılıyor.
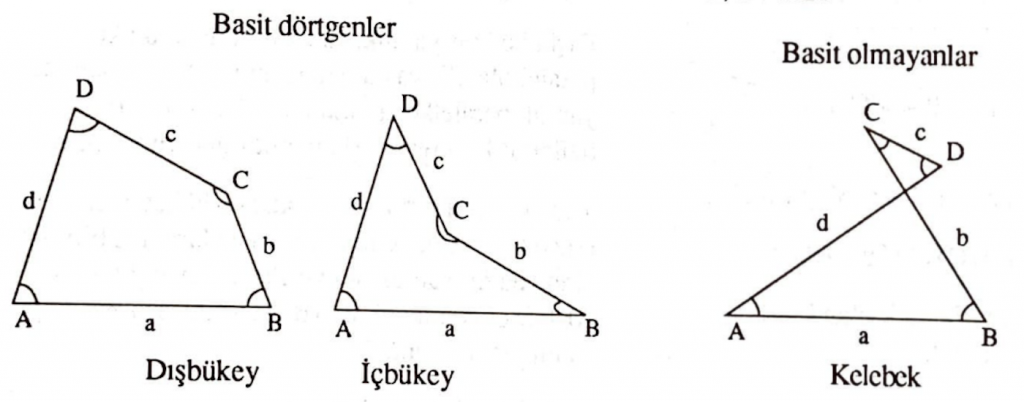
Kelebek dörtgenlere, çapraz ya da yıldıl dörtgenler de denir. Şekilde görüldüğü üzere basit dörtgenler dışbükey ve içbükey olmak üzere ikiye ayrılır. Dışbükey (içbükey) bir dörtgende herhangi bir doğru dörtgeni en çok iki (dört) noktada keser. Her ikisinin de bir iç ve dış bölgesi vardır. Basit olmayan bir dörtgende komşu olmayan iki kenar kesişirler ve şekil kelebeğe benzediği için kelebek adını alır.
Herhangi bir $ABCD$ dörtgeninde kenar uzunluklarını $$a=|AB|,\quad b=|BC|,\quad c=|CD|,\quad d=|DA|$$ olarak gösteririz. Karşılıklı köşeleri birleştiren doğru parçalarına da köşegen denir. Bunların uzunluklarını da $$e=|AC|,\quad f=|BD|$$ olarak gösteririz.
Açılara gelince pozitif ölçüleri $$A=\sphericalangle{BAD},\quad B=\sphericalangle{CBA},\quad C=\sphericalangle{DCB},\quad D=\sphericalangle{ADC}$$ olarak yazarız.
Dışbükey dörtgenlerde bazı simgeler
$S=|ABCD|$ (dörtgenin alanı)
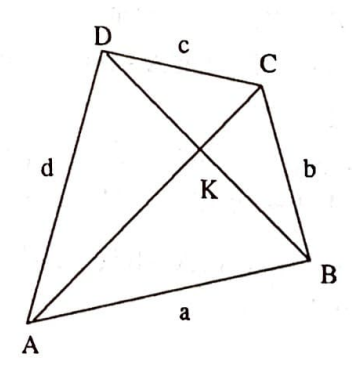
Bir köşegeni kenar kabul eden üçgenlerin alan, çevrel yarıçap ve iç yarıçaplarını $S_A$, $S_B$, $S_C$, $S_D$; $R_A$, $R_B$, $R_C$, $R_D$ ve $r_A$, $r_B$, $r_C$, $r_D$ ile gösteriyoruz. Örneğin $S_A$ dediğimizde $A$ köşesinin karşısındaki köşegeni kenar kabul eden $ABD$ üçgeninin alanı anlaşılacaktır.
Bir köşesi $K$ köşegen noktası olan üçgenlerin alanları, çevrel yarıçapları ve iç yarıçapları için $S_a$, $S_b$, $S_c$, $S_d$; $R_a$, $R_b$, $R_c$, $R_d$ ve $r_a$, $r_b$, $r_c$, $r_d$ simgelerini kullanacağız.
Basit dörtgenlerin alan formülü
Kenarları verilen bir dörtgen çeşitli biçimler alabileceğinden alanının kenarlar türünden ifade edilemeyeceği açık olup $$\varphi=\frac{A+C}{2}\qquad \text{ ya da }\qquad \varphi’=\frac{B+D}{2}$$ parametresini seçelim. $\varphi+\varphi’=\pi$ olup $\cos^2\varphi =\cos^2\varphi’$’dir.
Teorem: Kenar uzunlukları $a$, $b$, $c$, $d$, yarı çevresi $u$ ve parametresi $\varphi=\frac{A+C}{2}$ olan basit bir $ABCD$ dörtgeninin alanı için $$\boxed{ S^2=(u-a)(u-b)(u-c)(u-d)-abcd\cos^2\varphi}\tag{1}$$ formülü geçerlidir.
İspat: $$\begin{split} 2S &=S_A+S_C=ad\sin A + bc\sin C\\
\implies 4S^2 &= a^2d^2 \sin^2A +b^2c^2\sin^2C + 2abcd \sin A \sin C \\
&= a^2d^2 (1-\cos^2A) + b^2c^2(1-\cos^2C) + 2abcd \sin A \sin C \\
&= a^2d^2 + b^2c^2\, -\, a^2d^2\cos^2A\, -\, b^2c^2\cos^2C + 2abcd \sin A \sin C \end{split}$$ olup, $$\begin{split} &1+\cos(A+C)=2\cos^2\varphi\\
\implies & 1 + \cos A\cos C -\sin A \sin C =2\cos^2\varphi \end{split}$$ kullanıldığında
$$\begin{split} 4S^2 &= a^2d^2 + b^2c^2\, -\, (a^2d^2\cos^2A + b^2c^2\cos^2C) + 2abcd (1 +\cos A\cos C \,-\, 2\cos^2\varphi) \\
&=(ad+bc)^2 -(ad\cos A \,-\, bc\cos C)^2 -4abcd \cos^2 \varphi \\
16S^2 &= (2ad+2bc)^2 -(2ad\cos A \,-\, 2bc\cos C)^2 -16abcd \cos^2 \varphi \end{split}$$ elde edilir.
İkinci parantezde kosinüs teoremi uygulandığında $(a^2 + d^2 -b^2 -c^2)^2$ bulunur ve sağ taraftaki iki kare farkı çarpanlara ayrılıp kısaltmalar yapılırsa $(1)$ elde edilir. $\square$
Şimdi, aynı tür elemanlar (kenarlar, köşegenler, açılar) arasına bir takım koşullar koyarak özel bazı dörtgenleri elde edeceğiz.
A. Yamuklar
Karşılıklı iki kenar paralel olan bir dörtgene yamuk denir.
Bu kenarlar $[AB]$ ve $[CD]$ ise bunlara taban adı verilir. Öteki iki kenara da yan kenarlar denir.
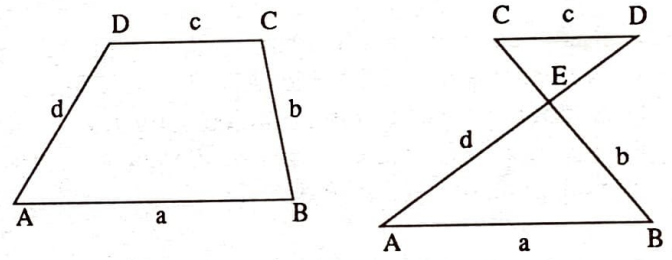
İçbükey bir dörtgen yamuk olamayacağından dışbükey ve kelebek yamuktan söz edilebilir.
Dışbükey bir yamukta karşılıklı öteki iki kenar paralel olabilir ya da olmayabilir. Olması halinde yamuk paralelkenar adını alır. Bunun da özel halleri dikdörtgen, eşkenar dörtgen ve karedir.
Taban açıları birbirine eş olan dışbükey yamuğa ikizkenar yamuk denir. Taban açılarından biri dik olana da dikyamuk adı verilir. Herhangi bir $ABCD$ dikyamuğunda $AB\perp BC \perp CD$ ise $[DA]$’ya hipotenüs denilebilir.
Dışbükey bir yamuğun alanı $$S=|ABCD|= |EAB|+|ECD|=\frac{1}{2}\frac{a^2+c^2}{a+c}h$$ olduğu gösterilebilir (Bkz. Alıştırma 2).
B. Dikgen Dörtgenler
Köşegenleri birbirine dik olan bir dörtgene dikgen dörtgen deriz.
Üç sınıfta da dikgen dörtgen var.
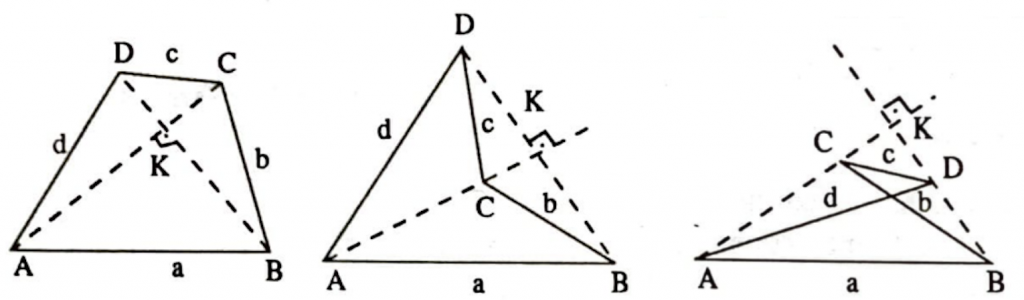
Teorem: $$\text{Dikgen } ABCD \iff a^2+c^2=b^2+d^2$$
İspat: $B$ ve $D$’nin $AC$ üzerindeki dik izdüşümleri $B’$, $D’$ ise $a^2-b^2=|AB’|^2-|CB’|^2$ ve $d^2-c^2=|AD’|^2-|CD’|^2$’den dikgen $ABCD \iff a^2+c^2=b^2+d^2$. $\square$
C. Kiriş Dörtgenleri
Köşeleri bir çember üzerinde bulunan bir dörtgene kirişler dörtgeni diyoruz.
Sadece dışbükey ve kelebek dörtgenler kirişler dörtgeni olabilir.
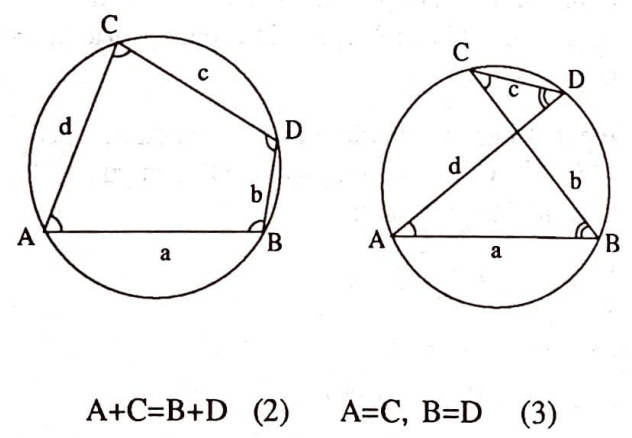
Kirişler dörtgeninde açılar için $(2)$ ve $(3)$ bağıntıları sırasıyla dışbükey ve kelebek dörtgenler için geçerli olup gerek ve yeter koşullardır.
Kirişler dörtgeninde ilginç bir teorem Batlamyus (M.S. 130) teoremidir:
Teorem: (Batlamyus) Dışbükey bir kirişler dörtgeninde, karşılıklı kenarların uzunluklarının çarpımlarının toplamı köşegen uzunluklarının çarpımını eşittir. $$ac+bd=ef\tag{4}$$
İspat: İspatta, kenar uzunlukları $a$, $b$, $c$ olan bir üçgende $$bc=2Rh_a\tag{5}$$ bağıntısından yararlanacağız. Bu amaçla $C$’den $DA$’ya paralel $[CC’]$ kirişini çizip $[DC]$’yi $[AC’]$’ye taşıyalım. $AC’B$ üçgeninde $(5)$’i kullanarak $$ac=2Rh’ \tag{5$^{\prime}$}$$ yazalım.
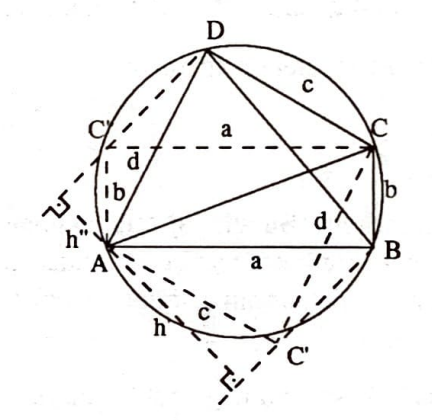
Bu sefer $C$’den $BA$’ya paralel $[CC^{\prime\prime}]$ kirişini çizip $[BC]$’yi $[AC^{\prime\prime}]$’ye taşıyalım ve $ADC^{\prime\prime}$ üçgenine $(5)$’i uygulayalım. Şu eşitlik elde edilir: $$bd=2Rh^{\prime\prime}.\tag{5$^{\prime\prime}$}$$
$BC’// DC^{\prime\prime}$ olduğu $BCD$ ve $C’AC^{\prime\prime}$ yaylarının eşliğinden kolayca görülür. $(5^\prime)$ ve $(5^{\prime\prime})$’in taraf tarafa toplanmasıyla
$$ac + bd = 2R(h’+h^{\prime\prime})=2Rh $$ çıkar. Burada $h$ uzunluğu, paralel olan $BC’$, $DC^{\prime\prime}$ doğrularının uzaklığıdır.
Öte yandan $e=|AC|=|DC’|$ olup $DC’B$ üçgenine $(5)$ uygulandığında $$ ef=2Rh$$ bulunur ki $ac + bd = ef $ eşitliği ispatlanmış olur. $\square$
Batlamyus’tan çok sonraki matematikçiler şu genel teoremi elde etmişlerdir:
Teorem: Basit bir $ABCD$ dörtgeninde $$ac+bd \geq ef \tag{6}$$ eşitsizliği geçerli olup eşitlik ancak dörtgenin kirişler dörtgeni olması halinde sağlanır.
Bu teoremin evirtimle yapılan ispatı dergimizde yer almıştır [Cilt II, Sayı 2, s. 8].
Batlamyus teoreminin en basit uygulaması olarak şu teoremi elde edebilirsiniz:
Teorem: Eşkenar bir $ABC$ üçgeninin çevrel çemberinin $A$ karşısındaki yay üzerinde alınan bir $P$ noktasının $A$’dan uzaklığı, $B$ ve $C$’den olan uzaklıklarının toplamına eşittir.
Şimdi bir kirişler dörtgeninde köşegen uzunluklarının $e/f$ oranı ile ilgili teoremi verelim:
Teorem: Bir kirişler dörtgeninde $$\frac{e}{f} = \frac{ad+bc}{ab+cd} \tag{7}$$ eşitliği geçerlidir. (Burada sağ taraftaki oranda pay ve payda, ilgili köşegenin uçlarından geçen kenarların uzunluklarının çarpımının toplamını ifade etmektedir.)
İspat: $[BD]$ köşegenini çizmekle oluşan üçgenlerin alanları
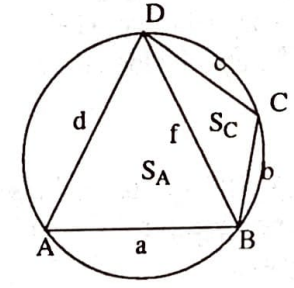
$$4RS_A=daf,\quad 4RS_C=bcf$$
olarak bilinmekte olup $$4RS = 4R(S_A+S_C) = (ad+bc)f$$ olur. Benzer olarak $$4RS = 4R(S_B+S_D) = (ab+cd)e$$ olup her iki eşitlik taraf tarafa bölünerek $(7)$ elde edilir. $\square$
Sonuçlar: Yukarıda elde edilen formülleri kullanarak $$\begin{split} e^2 & = \frac{(ad+bc)(ac+bd)}{ab+cd} \\ f^2 &=\frac{(ac+bd)(ab+cd)}{ad+bc} \end{split}\tag{8}$$ eşitliklerini buluruz.
Uygulama: Batlamyus teoremini kullanarak üçgenler için bilinen Carnot teoremini ispatlayabiliriz.
Teorem: (Carnot) Bir $ABC$ üçgeninde çevrel merkezin kenarlardan olan yönlü uzaklıkları toplamı, çevrel ve iç yarıçapların toplamına eşittir. $$\chi_a +\chi_b +\chi_c = R+r \tag{9}$$
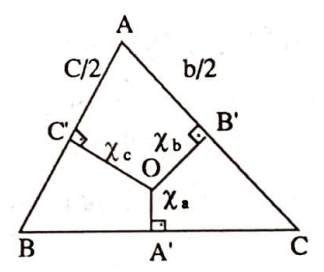
(Not: Örneğin $A$ açısı genişse çevrel $O$ merkezi üçgenin dışında ve $A$ açısı içinde olup $\chi_a$ uzaklığı negatif alınır.)
İspat: Üçgenin kenarlarının orta noktaları $A’$, $B’$, $C’$ ise $AC’OB’$ kirişler dörtgenine Batlamyus teoremine uygulayalım: $$\frac{1}{2}c\chi_b+\frac{1}{2}b\chi_c = \frac{1}{2}aR \; \implies \; c\chi_b+b\chi_c = aR$$ elde edilir. Benzer olarak $$a\chi_c+c\chi_a = bR,\quad b\chi_a+a\chi_b = cR $$ geçerli olup üçünün taraf tarafa toplanmasıyla $$a(\chi_b+\chi_c)+b(\chi_a+\chi_c)+c(\chi_a+\chi_b) = 2uR $$ çıkar. Öte yandan $$a(\chi_a+\chi_b+\chi_c)+b(\chi_a+\chi_b+\chi_c)+c(\chi_a+\chi_b+\chi+c) = 2u(R+r)$$ $$\implies \; 2u(\chi_a+\chi_b+\chi_c) = 2u(R+r)$$ çıkar ki $(9)$ elde edilmiş olur. $\square$
Şimdi kirişler çokgeni için Japon teoremini yazalım.
Teorem: (Japon) Bir kirişler $A_1A_2\ldots A_n$ çokgeninde $A_i$ kirişinden geçen köşegenlerin çizilmesiyle oluşan üçgenlerin iç yarıçapları toplamı $i$’den bağımsızdır.
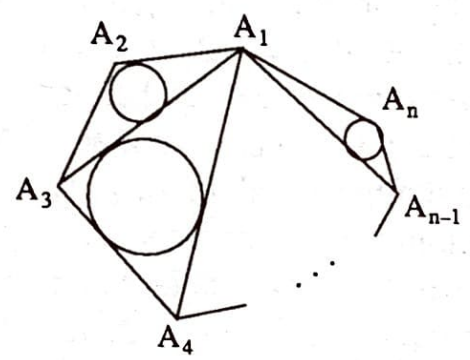
Teoremi dörtgenler için ispatlayacağız. Bu genel teorem tümevarımla ispatlanabilir.
İspat: ($n=4$) $A$’dan geçen köşegeni çizdiğimizde $ABC$, $ACD$ üçgenleri oluşur. Bunlara Carnot eşitliği uygulandığında
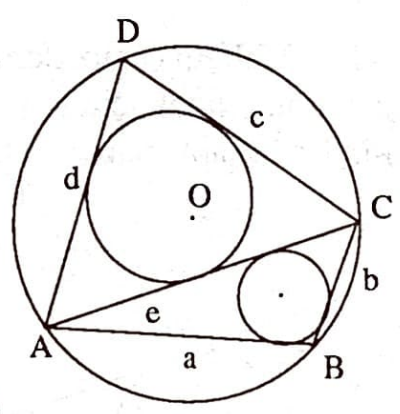
$$\begin{split} \chi_a+\chi_b-\chi_e &= R+r_B\\
\chi_c +\chi_d +\chi_e &= R+r_D\\
\implies \chi_a +\chi_b +\chi_c +\chi_d &= 2R+r_B+r_D \ .\end{split}$$ Buradan $r_B+r_D = (\sum \chi_i)-2R$ çıkar. Öteki köşegeni çizmekle benzer olarak $r_A+r_C = (\sum \chi_i)-2R$ bulunur. Böylece iddia ispatlanmış olur. $\square$
Sonuç: Basit dörtgenlerden kenar uzunlukları verilen en büyük alanlısı kirişler dörtgenidir: $$S^2=(u-a)(u-b)(u-c)(u-d)-abcd\cos^2\varphi $$ olup $$\max S \implies \min \cos^2\varphi \implies \cos^2\varphi=0 \implies \varphi = \frac{A+C}{2}=\frac{\pi}{2} \implies A+C=\pi .$$
O halde $ABCD$ kirişler dörtgeninin alan formülü $$S=\sqrt{(u-a)(u-b)(u-c)(u-d)}\qquad \text{(Brahmagupta)}\tag{10}$$olur.
Alıştırmalar
- Dışbükey bir $ABCD$ dörtgeninde $$S_aS_c=S_bS_d \tag{11}$$nin geçerli olduğunu gösteriniz.
- Taban uzunlukları $a$, $c$ yüksekliği $h$ olan kelebek bir yamuğun alanının (kanatların alanları toplamının) $$\frac{1}{2}\frac{a^2+c^2}{a+c}h \tag{12}$$ olduğunu gösteriniz.
- Dışbükey bir yamukta $$\sqrt{S} = \sqrt{S_a} +\sqrt{S_c}\tag{13}$$ olduğunu gösteriniz.
- Kenar uzunlukları $4$, $3$, $5$, $2$ ve parametresi $\varphi=60$ olan dışbükey dörtgenin alanını hesaplayınız.
- Ardışık kenar uzunlukları $\sqrt{2}$, $\sqrt{7}$, $\sqrt{5}$, $x$ olan bir dörtgen $x$’in hangi değeri için dikgendir?
- Dikgen bir $ABCD$ dörtgeninde $$r_a+r_b+r_c+r_d = e+f-u$$ eşitliği geçerlidir. (Alasia)
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1993 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Zeynep K‘ye ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

