Yazar: Halil İbrahim Karakaş
Sayı: 1992-4
$S$ boş olmayan bir seçenekler kümesi olsun. $S$’nin elemanları, bir toplumun bireylerinin tercihlerini açıklayabilecekleri herhangi bir kişi, nesne veya görüş olabilir. Örneğin, $S$ (başkanlık sistemi ile yönetilen) bir ülkede başkanlık seçimlerine katılan adayların kümesi veya bir kentte belli bir arsanın hangi amaçla kullanılabileceği konusunda değişik görüşlerin kümesi olabilir.
$S$ içinde tanımlı tüm kısmi sıralama bağıntılarının (kısıba) kümesini $\kappa$ ile göstereceğiz. Örneğin, $S = \{a, b\}$ ise, $\kappa$’nin elemanları Hasse çizelgeleriyle gösterilerek,
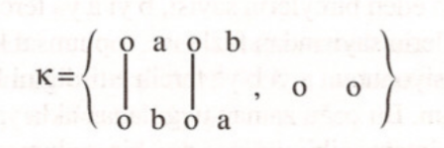
olduğu görülür. $S$ içindeki tüm zayıf sıralama bağıntılarından oluşan kümeyi $Z$ ile göstereceğiz. $S= \{a,b\}$ için $Z=\kappa$’dir. Üç elemanlı bir küme içinde 19 kısmi sıralama bağıntısı bulunduğu ve bunlardan sadece 13’ünün zayıf sıralama bağıntısı olduğu görülebilir.
Bir toplumun her bir bireyinin $S$’yi kendince kısmi sıralaması durumunda, bireylerin görüşlerini de göz önüne alarak, toplumun $S$’yi kısmi sıralarken izleyebileceği yolların neler olduğunu araştırmak istiyoruz. Böylece $S$ hakkında verilecek toplumsal kararı, bireylerin kararlarının bir fonksiyonu olarak düşüneceğiz. Daha açık bir ifadeyle, $\kappa$’nin iki alt kümesini ele alacağız: $X$ ve $Y$. Bunlardan $X$, bireylerin $S$ içinde belirlemelerine izin verilen kısmi sıralama bağıntılarından oluşan altküme, $Y$ ise toplumun ($S$ içinde) belirlemesine izin verilen kısmi sıralama bağıntılarından oluşan altkümedir.
Toplumun $S$ hakkında alacağı bir kararda rolü olacak bireylerin sayısı $n$ olsun. Bu takdirde, bir toplumsal karar fonksiyonu, tanım bölgesi $X\times X\times\dots\times X=X^n$ ve değer bölgesi $Y$ olan bir fonksiyondur: $f: X^n\rightarrow Y$. Tanım bölgesindeki her $(x_1,\dots,x_n)$ elemanı için $x_i$, $i$-inci bireyin $S$ içinde belirlediği kısmi sıralama bağıntısıdır.
Örnek olarak, bir ülkenin başkanlık seçimlerinde; $S$ adayların oluşturduğu küme, $n$ oy kullanabilir seçmenlerin sayısı ve $X$ de $S$ içinde izin verilen kısmi sıralama bağıntılarıdır. Bir seçmen, ya bir adayı diğerine tercih edeceği ya da oy kullanmaktan kaçınacağı için $X$, iki tür kısıbadan oluşur:
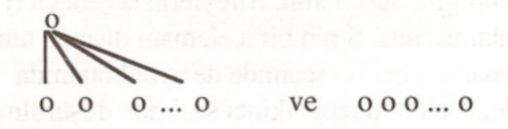
Bu tür bir seçimde, toplumsal karar fonksiyonu, yukarıdakilerden birinci tipte bir kısmi sıralama bağıntısı vermek durumundadır. Toplumsal karar fonksiyonunun verdiği kısmi sıralama bağıntısının büyükçe elemanı en çok oy alan aday olacaktır. Aynı çoklukta oy alan birkaç aday varsa, bu durumda seçim görevlisi veya görevlileri, sonucu kura ile belirleyebilir.
Çok değişik toplumsal karar verme yöntemleri ya da toplumsal karar fonksiyonları vardır. Bunlar arasında, yukarıdakine ek olarak, ağırlıklı oylama yöntemi ve tercihli oy yöntemi sayılabilir.
$S$, $X$, $Y$, $f$ ve $n$ yukarıdaki gibi olmak üzere, seçmenler kümesini
$$I_n=\{1,2,\dots,n\}$$
ile özdeştirelim. $a,b\in S$; $\kappa_1,\dots,\kappa_n\in X$ için $(a,b)\in\kappa_i$ ise $a\geq_i b$; $1\leq i\leq n$, $a$ ile $b$, $\kappa_i$’ye göre ayrımsız ise $a\sim_i b$; $1\leq i\leq n$, $a$ ile $b$, $f(\kappa_i,\dots,\kappa_n)$’e göre ayrımsız ise $a\sim b$, ve $(a,b)\in f(\kappa_1,\dots,\kappa_n)$ ise $a\geq b$ yazacağız. Benzer biçimde; $\kappa’_1,\dots,\kappa’_n\in X$ için $(a,b)\in\kappa’_i$ ise $a\geq_i’ b$; $1\leq i\leq n$, $a$ ile $b$, $\kappa’_i$’ye göre ayrımsız ise $a\sim_i’ b$; $1\leq i\leq n$, $a$ ile $b$, $f(\kappa’_i,\dots,\kappa’_n)$’e göre ayrımsız ise $a\sim’ b$, ve $(a,b)\in f(\kappa’_1,\dots,\kappa’_n)$ ise $a\geq’ b$ yazacağız.
Aynı seçenekler kümesi üzerinde iki kez seçim yapıldığını düşünelim. Bireylerin seçenekleri sıralamasında, $S$’nin bir $a$ elemanı dışında tüm elemanları her iki seçimde de aynı konumda kalmış, $a$’nın düzeyi ikinci seçimde düşürülmüş ve toplumsal karar fonksiyonu birinci seçimde $a$’yı bir $b$ seçeneğine tercih etmiş ise, ikinci seçimde de $a$’yı $b$’ye tercih etmesi arzu edilen bir özelliktir. Bu özellik, sembolik olarak şöyle ifade edilir.
Birinci Özellik: $a,b\in S$; $\kappa_1,\dots,\kappa_n;\kappa’_1,\dots,\kappa’_n\in X$ olsun. Her $c,d\in S$, $c\neq a$, $d\neq a$, ve $i\in I_n$ için $c\geq_i d\leftrightarrow c\geq’_i d$ olduğunu ve her $e\in S$ $a\geq_i e \implies a\geq’_i e$ olduğunu kabul edelim. Bu takdirde $a\geq b\implies a\geq’ b$ olur.
Toplumsal karar fonksiyonunun arzu edilen bir diğer özelliği, herhangi iki seçenek arasında yapılacak toplumsal tercihin sadece ve sadece o seçenekler arasında bireylerin yapacakları tercihlerle ortaya çıkmasını sağlamasıdır. Sembolik ifade ile,
İkinci Özellik: $a,b\in S$; $\kappa_1,\dots,\kappa_n;\kappa’_1,\dots,\kappa’_n\in X$ olsun. Eğer her $i,j=1,\dots,n$ için $a\geq_i b\leftrightarrow a\geq’_i b$ ve $b\geq_i a\leftrightarrow b\geq’_i a$ ise bu takdirde $a\geq b\Leftrightarrow a\geq’ b$ olur.
Herhangi bir seçim sonunda, toplumsal karar fonksiyonu uygulandığında, bir toplumsal tercihin ortaya çıkması arzu edilir. Yukarıdaki iki özelliği sağladığı halde, bir toplumsal tercih ortaya koymayan karar fonksiyonları vardır. Örneğin, bir seçimde $a$ seçeneğini $b$ seçeneğine tercih eden bireylerin sayısı, $b$’yi $a$’ya tercih edenlerin sayısından fazla ise, toplumsal karar fonksiyonunun $a$’yı $b$’ye tercih ettirdiğini kabul edelim. Bu çoğu zaman uygulanan akla yatkın bir yöntem gibi görünse de, bir toplumsal tercih ortaya koymayabilir. Şöyle ki, üç seçenekli, yani $S=\{a,b,c\}$ ve üç seçmenli bir seçimde, seçmenlerin seçenekler kümesi aşağıda verilen Hasse Çizelgelerinde görüldüğü gibi sıraladıklarını varsayalım:
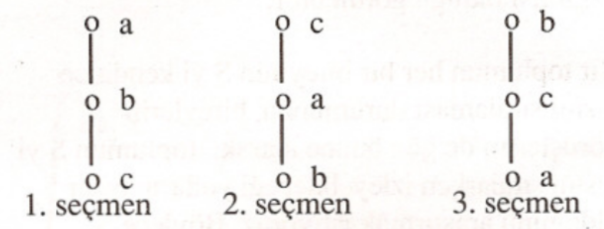
Burada, $a$’yı $b$’ye, $b$’yi $c$’ye ve $c$’yi $a$’ya tercih edenlerin sayıları aynıdır. Bu nedenle, toplumsal karar fonksiyonu ile elde edilecek bağıntı geçişme özelliğine sahip olmaz. Daha açık bir deyimle, bir toplumsal tercih ortaya çıkmaz.
Toplumsal karar fonksiyonunun bir toplumsal tercih ortaya koyamadığı durumlarda, dışardan müdahalelerle toplumsal tercih oluşturulmaya çalışılır. Örneğin, bazı tabular, dinsel baskılar veya baskı yasaları gibi. Bazen de, toplumsal tercihi bir kişi ya da bir grubun belirlemesi yoluna gidilir. Uygar, demokratik toplumlarda, toplumsal tercihin, müdahalerle veya ayrıcalıklı kişi ya da kurumların isteği doğrultusunda belirlemesi arzu edilmez. Bu nedenle, toplumsal karar fonksiyonun arzu edilen özelliklerine aşağıdaki iki özelliği de katmak gerekir:
Üçüncü Özellik: Her $a,b\in S$, $a\neq b$, için $(a,b)\in f(\kappa_1,\dots,\kappa_n)$ olacak biçimde $\kappa_1,\dots,\kappa_n\in X$ vardır.
Dördüncü Özellik: Seçmenler kümesi $I_n$’in boş olmayan bir öz-altkümesi $J$ ve her $j\in J$ için $\kappa_j\in X$ verilmiş olsun. $a,b\in S$, $a\neq b$ ve her $j\in J$ için $a\geq_i b$ ise bu takdirde $(a,b)\not\in f(\kappa_1,\dots,\kappa_n)$ olacak biçimde $\{\kappa_i\in X: i\in I_n\setminus J \}$ vardır.
Yukarıdaki üçüncü özellik, toplumsal karara dış baskı olmaması, dördüncü özellik ise toplumsal kararı ayrıcalıklı bir kişi ya da grubun belirlememesi gerektiğini ifade etmektedir.
Ne yazık ki, yukarıda verilen özelliklerin hepsini birden sağlayan bir toplumsal karar fonksiyonu yoktur. Şimdi 1951 yılı ekonomi dalında Nobel ödülünü kazanan K. Arrow’a ait olan ve “Seçim Paradoksu” olarak da bilinen bu sonucun ispatı için hazırlık yapacağız.
Bunun için, dördüncü özellikle yakından ilgili olan karar kümesi kavramını tanımlayacağız: $a,b\in S$, $a\neq b$ ve $J\subseteq I_n$ olsun. Eğer $\kappa_1,\dots,\kappa_n\in Z$ ve her $j\in J$ için $a>_j b\implies a>b$ ise bu takdirde $J$’ye $(a,b)$’nin karar kümesi denir.
Bir karar fonksiyonunun sahip olması arzu edilen özelliklerden dördüncüsü, $I_n$’nin boş olmayan hiç bir öz-altkümesinin $(a, b)$’nin karar kümesi olmaması gerektiğini ifade eder.
Teorem 1: Birinci ve ikinci özellikleri sağlayan bir toplumsal karar fonksiyonu $f:Z’\rightarrow Z$ verilmiş olsun. $a,b\in S$ $a\neq b$, $j\subseteq I$ ve $K=I_n\setminus J$ olsun. Eğer her $j\in J$ için $a>_j b$ ve her $k\in K$ için $b>_k a$ olacak biçimde $\kappa_1,\dots,\kappa_n \in Z$ varsa ve $a>b$ ise bu takdirde $J$, $(a,b)$’nin karar kümesidir.
İspat: Her $j\in J$ için $a>’_j b$ olan $\kappa’_1,\dots,\kappa’_n\in Z$ düşünelim. $J$’nin $(a,b)$’nin karar kümesi olduğunu, yani $a>b$ olduğunu göstermek istiyoruz. Bunun için varsayımda verilen $\kappa_1,\dots,\kappa_n$’yi öyle yeni $\kappa”_1,\dots,\kappa”_n\in Z$ ile değiştireceğiz ki aşağıdaki iki şart olsun.
i) her $i\in I$ ve $c,d\in S$, $c\neq a$, $d\neq a$ için $c>_i d\Leftrightarrow c>”_i d$ ver her $e\in S$ için $a>_i e \implies a>”_i e$ (böylece birinci özellikten $a>”b$) dir.
ii) her $i\in I_n$ için $a\geq_i b\Leftrightarrow a\geq”_i b$ ve $b\geq_i a \Leftrightarrow b\geq”_i a$ (böylece ikinci özellikten $a>’b$) dir.
Bunu gerçekleştirmek için, $I_h$’nin aşağıdaki alt kümelerini düşünelim:
$$L=\{l: b>_l a \; \text{ve}\; a>’_l b\}$$
$$M=\{m: b>_m a\; \text{ve}\; a\sim’_m b\}$$
$$H=\{h: b>_h a\;\text{ve}\; b>’_h a\}$$
Açıkça göründüğü üzere $K=L\cup M\cup H$ olup $\{J,L,M,H\}$, $I_n$’nin bir parçalanışıdır.
$a$ ve $b$’ye $\kappa_1,\dots,\kappa_n$’nin ve $\kappa’_1,\dots,\kappa’_n$’nin etkileri $I_n$’nin her parçası için aşağıdaki çizelgelerle gösterilmiştir.
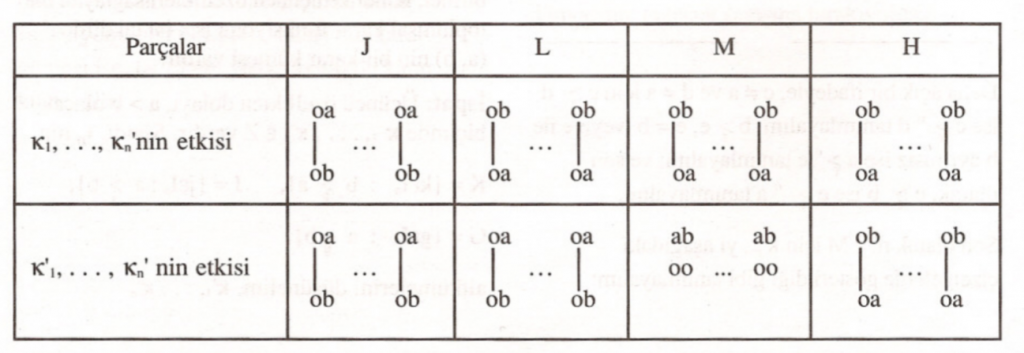
Şimdi $\kappa”_1,\dots,\kappa”_n$’yi $J, L, M$ ve $H$’deki seçmenler için ayrı ayrı aşağıdaki gibi tanımlayalım. Her $l\in J$ ve $h\in H$ için $k_j=k”_j$ ve $k_h=k”_h$ olsun. $l\in L$ için $\kappa”_l$, $a$’nın $\kappa_l$’nin çizelgesindeki konumu $b$’nin hemen üzerine gelecek şekilde değiştirilip, başka hiçbir seçeneğin yeri değiştirilmeden, aşağıdaki çizelgede gösterildiği gibi, elde edilsin:
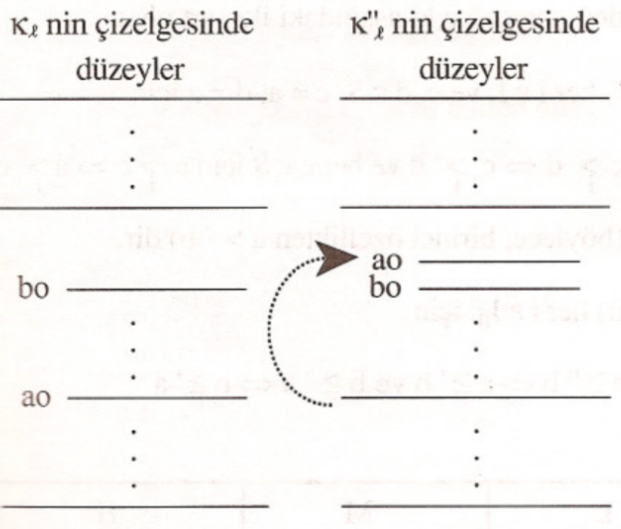
Daha açık ifadeyle, $c\neq a$ ve $d\neq a$ için $c>_l d$ ise $c>”_l d$ tanımlayalım, $b>_l e$, $e=b$ veya $e$ ile $b$ ayrımsız ise $a>”_i e$ tanımlayalım; ve son olarak, $e>_l b$ ise $e>”_l a$ tanımlayalım.
Son olarak $m\in M$ için $\kappa”_m$’yi aşağıdaki çizelgelerde gösterildiği gibi tanımlayalım:
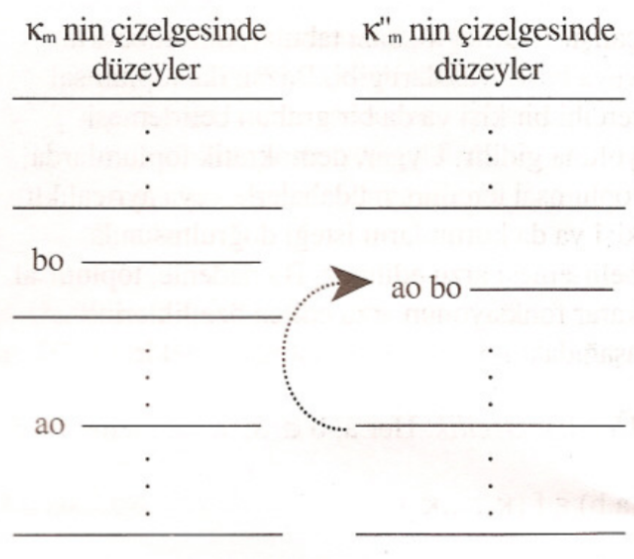
Çizelgelerden de görüldüğü üzere $\kappa”_m$, $a$’nın $\kappa_m$’nin çizelgesindeki konumu $b$’nin düzeyine getirilip başka hiçbir seçeneğin yeri değiştirilmeden elde edilmiştir. Bunu biraz açarsak, $c \neq a$ ve $d\neq a$ için $c >_m d$ ise $c >”_m d$ tanımlıyoruz, herhangi bir $e$ için $b >_m e$ ise $a >”_m e$ ve $e >_i b$ ise $e >_i a$ tanımlıyoruz.
Böylece tanımlanan $\kappa”_1,\dots,\kappa”m$ zayıf sıralama bağıntıları olup, birinci özelliğin hipotezi, $a, b \in S$ ve $\kappa_1,\dots,\kappa_n,\kappa”_1,\dots,\kappa”_n$ için sağlanmaktadır. O halde $a>” b$ dir. Ayrıca, $\kappa”_1,\dots,\kappa”_n$’nin tanımından dolayı her $t=1,\dots,n$ için $a>_t b\Leftrightarrow a>_t b$ ve $b>_t a\Leftrightarrow b>_t a$ dır. İkinci özellik sağlandığından, $a>’ b$ olduğu sonucu çıkar. Bu, teoremin ispatını tamamlar.
Teorem 1, $(a, b)$’nin bir karar kümesine sahip olması için bir yeter şart içermektedir. Aşağıdaki teorem, üçüncü özelliğin Teorem 1’deki şartın sağlanması için yeterli olduğunu göstermektedir.
Teorem 2: $a, b\in S$, ve $f : Z’ \rightarrow Z$ birinci, ikinci ve üçüncü özellikleri sağlayan bir toplumsal karar fonksiyonu ise, bu takdirde $(a, b)$’nin bir karar kümesi vardır.
İspat: Üçüncü özellikten dolayı, $a>b$ olacak biçimde $\kappa_1,\dots,\kappa_n\in Z$ vardır. Şimdi $I_n$’nin $=\{k\in I_n: b>_k a\}$, $J=\{j\in I_n: a>_j b\}$ ve $G=\{g\in I_n: a\sim_g b\}$ altkümelerini düşünelim. $\kappa’_1,\dots,\kappa’_n$ bağıntılarını her $i\in I_n\setminus G$ için $\kappa’_i=\kappa_i$ ve her $g \in G$ için aşağıdaki çizelgede görüldüğü gibi tanımlayalım:
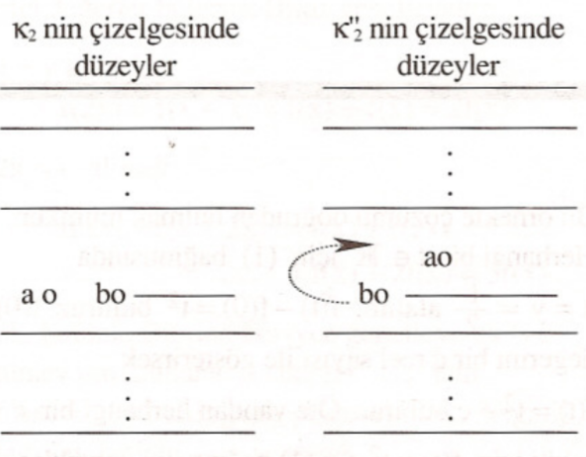
$\kappa’_1,\dots,\kappa’_n\in Z$ dir ve $a,b\in S$ ve $\kappa_1,\dots,\kappa_n,\kappa’_1,\dots,\kappa’_n$ için birinci özelliğin hipotezi sağlanır. Bu nedenle, $a>’b$ dir. Böylece $\kappa_1,\dots,\kappa_n$ bağıntıları ve $J$ kümesi Teorem 1’in hipotezini sağlarlar ve sonuç olarak $J$ kümesi $(a, b)$’nin karar kümesidir.
Üçüncü özellik sağlandığı sürece, bir karar kümesi boş olamaz. Çünkü, aksi takdirde, $\kappa_1,\dots,\kappa_n$ ne olursa olsun $a>b$ olur. Oysa, üçüncü özelliğe göre $b >a$ veren bağıntılar da vardır.
$a, b \in S$, $a\neq b$ için $(a, b)$’nin bir karar kümesi bulunduğunu gördük. Acaba bu kümenin diğer seçenekler üzerindeki davranışı nasıldır? Aşağıda, bu sorunun sürpriz sayılabilecek bir cevabı bulunduğunu göreceğiz.
Teorem 3: $a, b, c\in S$ üç farklı seçenek, $J\subseteq I$, ve $f: Z^n \rightarrow Z$ birinci, ikinci ve üçüncü özelliklere sahip olan bir toplumsal karar fonksiyonu olsun. Eğer $J$, $(a, b)$’nin karar kümesi ise, $(a, c)$’nin ve $(c, b)$’nin de karar kümesidir.
İspat: Her $j\in J$ ve $k\not\in J$ için $a>_j b$, $b>_j c$: $b>_k c$, $c>_k a$ olacak biçimde $\kappa_1,\dots,\kappa_n\in Z$ seçelim. İspatın ilk kısmında olduğu gibi, $a > b$, $c > a$ ve buradan geçişme özelliği ile $c> b$ olduğu; Teorem 1’e göre $J$’nin $(c, b)$’nin karar kümesi olduğu görülür.
Sonuç: Sonuç: $f : Z^n \rightarrow Z$, birinci, ikinci ve üçüncü özelliklere sahip bir toplumsal karar fonksiyonu; $a, b, c, d\in S$, $a \neq b$, $c\neq d$ olsun. Eğer $J\subseteq I_n$, $(a, b) $’nin karar kümesi ise, $(c, d) $’nin de karar kümesidir.
İspat: $d\neq a$ ise, Teorem 3’e göre, $J$, $(a, d)$’nin karar kümesidir. Teorim 3 bir kez daha uygulanarak, $J$’nin $(c, d)$’nin karar kümesi olduğu görülür. $d=a$ ise, $d$ ve $a$’dan farklı üçüncü bir seçenek $s$ düşünelim. Teorem 3’e göre $J$, $(s, d)$’nin karar kümesidir. Yine aynı Teoreme göre $J$, $(c, d)$’nin bir karar kümesidir.
Buraya kadar elde edilen sonuçları şöyle özetleyebiliriz: Birinci, ikinci ve üçüncü özelliklere sahip olan bir toplumsal karar fonksiyonu için, $I_n$’nin, $a, b \in S,$ $a \neq b$ olmak üzere her $(a, b)$’nin karar kümesi olan bir altkümesi vardır. Bu karar kümesinin boş olmadığını daha önce gözlemiştik. Bu karar kümesi, boş olmamanın yanında, $I_n$’nin bir öz-altkümesidir, hatta, tek elemanlı bir küme, yani bir diktatörlüktür. “Seçim Paradoksu” olarak bilinen bu sonucun ispatını Matematik dünyasının gelecek sayısına bırakıyoruz.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı III. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Övünç Özgün Eker‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

