Yazar: Cem Tezer
Yıl: 1992-2
Sayı: 7
Geçen sayıdaki Evirtim 1 başlıklı yazıda kaldığımız yerden devam ediyoruz.
Örnek IV
Evirtim sayesinde bilinen teoremlerden yeni teoremler elde edilebilir.
Önce üçgen eşitsizliğini hatırlayalım:
Üçgen Eşitsizliği: Düzlemde birbirinden farklı herhangi $A, B, C$ noktaları için
$\vert AC \vert \leq \vert AB \vert + \vert BC \vert$
olup eşitlik ancak ve yalnız $A, B, C$ doğrudaş olup $B, A$ ve $C$ arasında kalırsa doğrudur.
Şimdi de önemli bir teoremi üçgen eşitsizliğinin evirtimi altında görünüşü olarak elde edelim:
Teorem 4.(“Batlamyus (M.S. 2. yüzyıl) Teoremi) Birbirinden farklı ve doğrudaş olmayan herhangi $A, B, C, D$ noktaları için
$ \vert AC \vert \vert BD \vert \leq \vert AB \vert \vert CD \vert + \vert BC \vert \vert AD \vert $
olup, eşitlik ancak ve yalnız $A, B, C, D$ noktalarının çemberde olup $AC, BD$ doğrularının da sözkonusuysa çember için kesişmeleri halinde doğrudur.
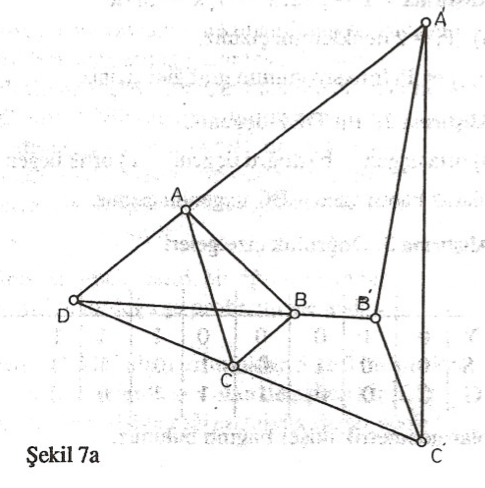
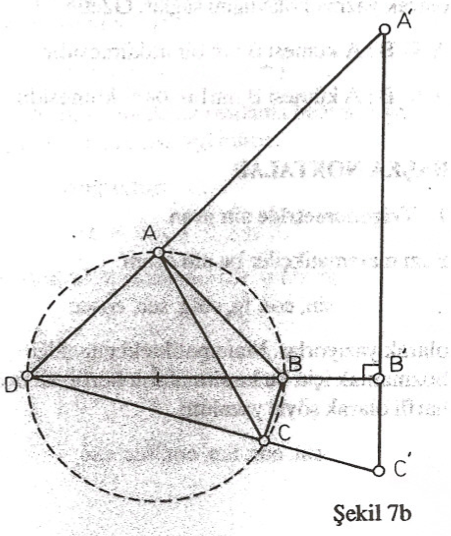
İspat: (Şekil 7a, 7b) Noktalardan bir tanesi geri kalan üç çiftten hiçbirisiyle doğrudaş olmayacaktır (Neden?) D bin bu özelliğe sahip olduğunu varsayalım. D merkezli bir evirdim alalım. Evirtimin kuvvetini (burada bir şey değiştirmemekle beraber) $\rho$ ile gösterelim. $A, B, C$ nin evrikleri sırasıyla $A’, B’, C’$ olsun (Şekil 7a).$DAB$ ve $DB’A’$ üçgenlerinin benzerliğinden ve $\vert DA \vert \vert DA’ \vert = \vert \rho \vert $ dan
$\frac{\vert A’B’ \vert}{\vert AB \vert} = \frac{\vert DA’ \vert}{\vert DB \vert} = \frac{\vert DA’ \vert \vert DA \vert}{\vert DA \vert \vert DB \vert} = \frac{\vert \rho \vert}{\vert DA \vert \vert DB \vert} $
ve
$ \vert A’B’ \vert = \frac{\vert AB \vert}{\vert DA \vert \vert DB \vert} \rho (7)$
bulunur. Aynı şekilde
$ \vert B’C’ \vert = \frac{\vert BC \vert}{\vert DC \vert \vert DC \vert} \rho (8)$
$ \vert A’C’ \vert = \frac{\vert AC \vert}{\vert DA \vert \vert DC \vert} \rho (9)$
elde edilir. $A’B’C’$ üçgeninde üçgen eşitsizliği yani
$ \vert A’C’ \vert \leq \vert A’B’ \vert + \vert B’C’ \vert (10)$
ve $(7),(8),(9)$ yardımıyla
$\frac{\vert AC \vert}{\vert DA \vert \vert DC \vert} \vert \rho \vert \leq \frac{\vert AB \vert}{\vert DA \vert \vert DB \vert} \vert \rho \vert + \frac{\vert BC \vert}{\vert DB \vert \vert DC \vert} \vert \rho \vert $
bundan da her tarafı $\vert DA \vert \vert DB \vert \vert DC \vert$ ile çarpıp $\vert \rho \vert$ ile bölmek suretiyle aranılan eşitsizlik
$\vert AC \vert \vert BD \vert \leq \vert AB \vert \vert CD \vert + \vert BC \vert \vert AD \vert$
bulunur. Bu eşitsizliğin eşitlik haline düşmesi için gerek ve yeter şart $(10)$ eşitsizliğinin eşitlik haline düşmesidir. Yani $A’, B’, C’$ doğrudaş olmalı ve $B’, A’ ve C’$ arasında kalmalıdır. Bu da ancak ve yalnız $A, B, C, D$ nin çemberdaş olup $AC$ ve $BD$ doğrularının sözkonusuysa çember içinde kesişmeleriyle mümkündür (Şekil 7b).
Evirtim konusunu biraz daha açıp son örneğime geçmeden önce okuyucunun, Batlamyus teoremi yardımıyla çözebileceği üç problem sunmak istiyorum:
Problem 3: $ABC$ bir eşkenar üçgen, $X$ de $ABC$ nin çevrel çemberi üzerinde $B$ yi $C$ ye birleştiren kısa yay üzerinde bir nokta ise
$ \vert XA \vert = \vert XB \vert + \vert XC \vert$
olduğunu gösteriniz.
Problem 4: Kenar uzunluğu 1 olan bir düzgün beşgenin köşegen uzunluğunun $\frac{1+\sqrt{5}}{2}$ olduğunu ispat ediniz.
Problem 5: A açısı $120^{\circ}$ ye eşit veya $120^{\circ}$ den büyük bir $ABC$ üçgeni alalım. Herhangi bir $X$ noktası için
$\vert XA \vert + \vert XB \vert + \vert XC \vert \geq \vert AB \vert + \vert AC \vert$
eşitsizliğini ispat ediniz. Bu eşitsizliğin eşitlik haline gelmesi için gerek ve yeter şartını $X = A$ olduğunu gösteriniz. (İpucu: $CA$ üzerinde $\vert AB \vert = \vert AB’ \vert$ olacak şekilde bir $B’$ noktası alın. $A, B’$ ve $C$ arasında kalsın. Batlamyus teoremini $XABB’$ dörtgenine uygulayın.
Evirtimi bir yere kadar Öklid geometrisinin içinde tutan özellik, bu dönüşümün açıları mutlak değerce korumasıdır.
Teorem 5: Bir evirdim eğriler arasındaki açıların işaretini değiştirir, açılar mutlak değerce saklı kalır.
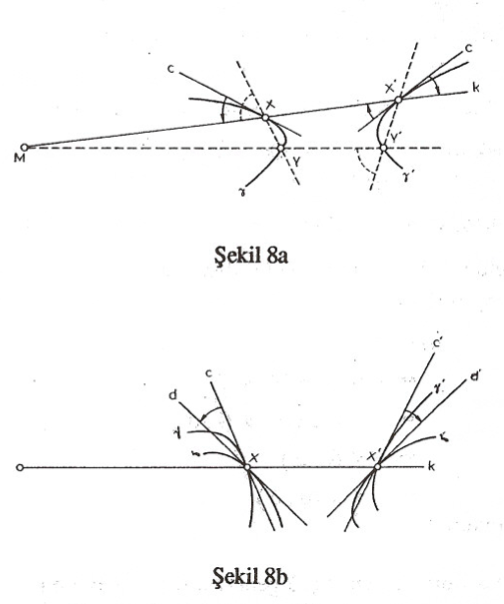
İspat: Önce kısaca “eğriler arasındaki açı” tabirine açıklık getirelim: $\gamma ve \delta$ gibi iki eğrinin bir $X$ noktasında kesiştiğini varsayalım (Şekil 8b). Eğrilerin $X$ noktasında yalnız birer teğete sahip olduklarını düşünelim. $\gamma$ ve $\delta$ anın $X$ noktasındaki teğetleri sırasıyla $c, d$ doğruları olsun. “$\gamma$ ve $\delta$ eğrileri arasında $X$ noktasındaki açı” ile $c$ ve $d$ doğruları arasındaki açı anlaşılacaktır. (Gösterim: $\sphericalangle X(\gamma, \delta))$. Şimdi ispata dönebiliriz: $M$ merkezli bir evirdim gözönüne alalım. $\gamma$ ve $\delta$ eğrileri $X ( \neq M)$ noktasında, sırasıyla bunların evrikleri olan $\gamma’$ ve $\delta’$ eğrileri de $X’$ noktasında kesişsinler (Şekil 8b). $X’, X$ in evrimidir. (Aslında, iki eğrinin X in belirli bir civarında yeniden kesişmedikleri vb. ikazlar gerekli. İspatı fazla karıştırmamak için bunları bir kenara bırakalım.) $\gamma, \delta$ nın $X$ deki teğetleri sırasıyla $c, d$ doğruları $\gamma’ \delta’$ nün $X’$deki teğetleri de sırasıyla $c’, d’$ olsun. Önce $\gamma$ eğrisine yönelelim (Şekil 8a). Bu eğri üzerinde $X$ e yakın (!) bir $Y$ noktası alalım. $Y$ nin evriği $Y’$ de $\gamma’$ üzerinde $X’$ ye yakın bir nokta olacaktır. $XX’ = MX$ doğrusu k ile gösterilecek ve $X, Y, Y’, X’$ noktalarının ya doğrudaş, yahut da çemberdeş oldukları hatırlanarak
$\sphericalangle (XY,k) = \sphericalangle (k, X’Y’) (11)$
bulunur. Y, X e yanaşırken ve Y’, X’ ne yanaşırken XY doğrusu c doğrusuna, X’Y’ doğrusu da c’ doğrusuna yanaşacaktır. Bunun neticesinde de (11) denklemi
$\sphericalangle (c,k) = \sphericalangle (k,c’) = – \sphericalangle (c’,k) (12)$
şeklini alacaktır. Aynı akıl yürütme, $\delta \delta’$ eğrilerine uygulanarak
$\sphericalangle(d,k) = \sphericalangle (k,d’) = – \sphericalangle (d’,k) (13)$
elde edilebilir. (12) ve (13) denklemleri kullanılarak
$\sphericalangle (\gamma, \delta) = \sphericalangle (c,d) = \sphericalangle (c,k) + \sphericalangle (k,d) = -\sphericalangle (c’,k) – \sphericalangle (k,d’) = -\sphericalangle (c’,d’) = – \sphericalangle x'(g’,\delta’)$
bulunur.
Yorum: Teorem 5 çok genel bir teorem. Biz bu teoremi sadece çemberler ve doğrulara o da yalnız $0^{\circ}$ ve $90^{\circ}$ için uygulayacağız. Yani: Bir evirdim birbirine dik (teğet) çember veya doğrulara dönüştürür. (Tabii, okuyucu paralel doğruları sonsuzda teğet çemberler olarak görmeli.)
Yardımcı Teorem 2. Pozitif kuvvetli bir evirtim, evirdim çemberine dik bir çemberi sabit bırakır.
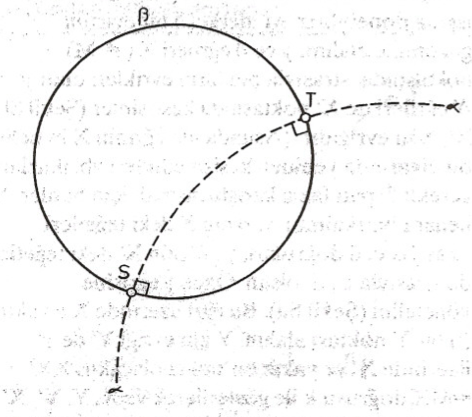
İspat: (Şekil 9) bir $\alpha$ çemberinde evirdim gözönüne alalım. $\beta \alpha$ çemberine $S, T$ noktalarında dik olsun. Evirdim, $S$ ve $T$ noktalarını sabit bırakmakta. Demek ki $beta$ nın evriği, $S$ ve $T$ noktalarında $\alpha$ ya dik bir çember olmalı ki bu $\beta$ nın kendisidir.
Örnek V
Kim ne derse desin benim için matematik tarihin şahikalarından biri olan Feuerbach Teoremini son örnek olarak ele alıyorum. Sözkonusuysa teoremi layıkıyla takdir edebilmesi için okuyucu bir üçgenin dokuz-nokta çemberini ve ilgili dokuyu biraz olsun tanımalıdır. Kısaca ele alalım:
Teorem6: Bir üçgende kenar orta noktaları, yükseklik ayakları ve üç yükseliğin kesiştiği noktayı (“ortosantr”) köşelere birleştiren doğru parçalarının orta noktaları çemberdeştir.
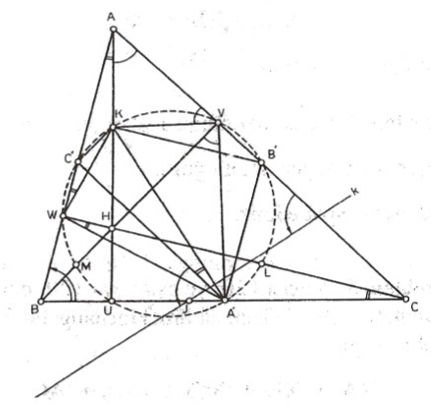
İspat: (Şekil 10). Bir $ABC$ üçgeni alalım. $A, B, C$ den karşı kenarlara indirilen dikmelerin ayakları sırasıyla $U, V, W$ ve $AU, BV, CW$ yüksekliklerinin kesiştiği nokta (“ortosantr”) $H$ olsun. Sırasıyla $[BC], [CA], [AB], [HA], [HB], [HC]$ doğru parçalarının orta noktaları $ A’, B’, C’, K, L, M$ olsun. Yapmak istediğimiz şey $ U, V, W A’, B’, C’, K, L, M$ noktalarını aynı çember üzerinde kaldığını görmek; sözkonusuysa çemberin $[A’K]$ çaplı çember olduğunu iddia ediyorum. $U$ aşikar bir şekilde $[A’K]$ çaplı çember üzerindedir. Diğer taraftan $B’, K$ sırasıyla $[CA]$ ve $[HA]$ nın orta noktaları olduğundan $B’, K, CW$ yüksekliğine paraleldir. $A’B’$ ve $AB$ ye paralel olduğundan $B’K, B’A’$ ye dik olmalıdır. Yani $B’$ noktası da $[A’K]$ çaplı çember üzerindedir. Aynı akıl yürütme $C’$ ne de uygulanabilir.
Gelelim $V$ ye: $AHV$ dik üçgendir; $K hipotenüsün orta noktasıdır. Demek ki $K AV$ (tepesi $K$ de olan) bir ikizkenar üçgen olup
$\sphericalangle (AV, KV) = \sphericalangle (AU,AC) = \sphericalangle (BC,BV)$ (Neden?)
dir. Diğer taraftan gene $BVC$ bir dik üçgen olduğundan ve $A’$ hipotenüsün orta noktası olduğundan $A’BV$ (tepesi $A’$ de olan) bir ikizkenar üçgendir. Böylece
$\sphericalangle (BC,BV) = \sphericalangle (BV, VA’)$
bundan da
$ \sphericalangle (AV,KV) = \sphericalangle (BV, VA’)$
bulunur. $AV, BV$ ye dik olduğundan, $KV$ de $VA’$ne dik olmalıdır. Yani $V, [A’K]$ çaplı çember üzerindedir. Aynı akıl yürütme $W$ noktasına da uygulanabilir. Bu suretle $A’, B’, C’, U, V, W, K$ noktalarının aynı çember $([A’K] çaplı çember)$ üzerinde kaldığını göstermiş olduk. $L$ ve $M$ ne olacak? Bunu okuyucuya bırakıyorum.
Yorum: Teorem6’da ele alınan çember, üzerinde dokuz tane ilginç nokta bulunduğundan “dokuz-nokta çemberi” ( veya “Euler çemberi”) olarak anılıyor. Bu çember üzerindeki ilk altı noktayı L. Euler (1707-1783) yakalamış. Noktaların sayısını dokuza çıkaran az sonra harikulade bir teoremini sunacağımız K. W. Feuerbach (1800-1834). Teorem6’daki dokuyla ilgili bir nokta daha:
Yardımcı Teorem 3: $BC$ kenarının $A$ daki içaçıortaya göre bakışığı $A’K$ doğrusuna diktir.
İspat: (Şekil 10) $A$ daki içaçıortay $BC$ yi $J$ noktasında kessin. $BC$ nin bu içaçıortaya göre bakışığına (simetriğine) $k$ diyelim. $k$ doğrusu da $J$ noktasından geçer ve
$ \sphericalangle (A’C’,k) = \sphericalangle (AC,k) = \sphericalangle (BC,BA)$
dir. Ayrıca
$ \sphericalangle (A’K,A’C’) = \sphericalangle (C’W,C’K) = \sphericalangle (BA,AU)$
olup, bu iki eşitlik taraf tarafa toplanarak
$ \sphericalangle (A’K, k) = \sphericalangle (A’K,A’C’) + \sphericalangle (A’,C’,k) = \sphericalangle (BA,AD) + \sphericalangle (BC,BA) = \sphericalangle (BC,AU = \frac{\pi}{2}$
bulunur.
Bu örneğin hedefi olan teoreme geçmeden önce evirdim hakkında bir noktaya daha işaret edilmesi gerekiyor:
Yardımcı Teorem 4: Bir k doğrusu üzerinde birbirinden farklı $A, B, X, X’$ noktaları alınsın. $X, X’$ noktalarının $[AB]$ çaplı çembere göre evrik noktalar olmaları için gerek ve yeter şart
$ \overline{XB} : \overline{XA} = – \overline{X’A} : \overline{X’B}$
olmasıdır.
İspat: Bunu okuyucuya bırakıyoruz. k doğrusunun x ekseni olarak seçip, basit bir hesap yapmak yeterli.
Teorem 7: (“Feuerbach Teoremi”) Bir üçgende dokuz-nokta çemberi iç ve dışteğet çemberlerle teğettir.
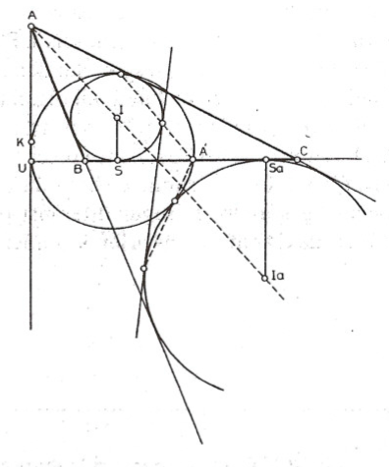
İspat: (Şekil 11) $ABC$ üçgeninin içteğet çemberinin merkezi $I, A$ karşısındaki dışteğet çemberin merkezide $I_a$ olsun. Bu çemberleri sırasıyla $(I), (I_a)$ nın $BC$ ye değdiği noktalar sırasıyla $S, S_a$ olsun. Bu belirtilenler dışında Teorem 4’ün gösterimini aynen alalım. Dokuz-nokta çemberinin $(I) ve (I_a)$ ya teğet olduklarını göstereceğiz. Diğer iki dışteğet çembere de aynı akıl yürütme uygulanabilir. $A, I, I_aE$ noktaları $A$ daki içaçıortay üzerinde olup, bu içaçıortay $BC$ yi $J$ de kesmekte. Gene $BC$ nin $AI$ ya göre bakışığı olan $k$ doğrusu da $J$ den geçmekte olup $(I)$ ve $(I_a)$ ya teğettir. (Neden?)
Son olarak da
$\overline{JS} : \overline{JS_a}$ = $-r : r_a$ = $-\overline{AI} : \overline{AI_a} = -\overline{US} : \overline{US_a}$
olduğunu gözleyelim. Diğer taraftan $A’$ (yani $[BC]$ nin orta noktası) $[SS_a]$ (Neden?) Yardımcı Teorem 4’e göre $[SS_a]$ çaplı çembere göre bir evirdim $J$ yi $U$ ya gönderecektir; evirtim merkezi de $A’$ noktasıdır. Demek ki $k$ doğrusunun evriği $U$ ve $A’$den geçen merkezi $A’$den $k$ ye indirilen dikme üzerinde yani Yardımcı Teorem 3’e göre $A’K$ üzerinde olan çember olmalıdır ki, bu ancak dokuz-nokta çemberidir. Yardımcı Teorem2’ye göre $(I)$ ve $(I_a)$ sözkonusuysa evirdim altında sabit kalırlar. Demek ki $k$ doğrusunun evriği olan dokuz-nokta çemberi de $k$ doğrusu gibi $(I)$ ve $(I_a)$ ya teğet olmalıdır.
Son olarak da konunun tarihini kısaca ele almak istiyorum: Evirtimin tarihi ne yazık ki açıklık kazanmamış bir saha. 17. yüzyılda henüz bilinmediği hakkında az çok anlaşma var. 19. yüzyılın ikinci çeyreğinde ise (mesela J. Plücker (1801-1863) tarafından) doğru olarak tarif edilmemiş ve hemen hemen bugünkü olgunluğu le geometride kullanılmış ([1]). Hemen arkasından W. Thomson (1824-1907), nam-ı diğer Lord Kelvin) tarafından evirtimin elektrostatiğe uygulandığı görülüyor. Bugün diferansiyel geometride konfor tasvirler, kompleks analizdeki Möbius dönüşümleri, cebirsel geometrideki Cremona dönüşümleri, ileri matematikte evirtimin genelleşmiş şekilleri olan dönüşümlerdir.
Kaynaklar
[1] J. L. Coolidge, “A Treatise on the Circle and the Sphere“, Chelsea Publishing Company, New York 1971 (İlk basım: Oxford, !916).
[2] H. Demir “Homoteti ve Benzerlik”, Matematik Dünyası, Sayı 4, s. 2-7.
[3] E. J. Dijksterhuis, “Archimedes“, Ejnar Munksgaard, Kopenhag, 1956. (C. Dikshoorn tarafından Felemenkçe aslından İngilizce’ye tercüme)
[4] C. Tezer, “Düzlem Geometride Açılar ve Ölçüleri”, Matematik Dünyası, Sayı 1, s. 3-6.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Melih Mert Oskay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

