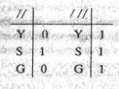Bazı Kavram, Tanım, Bağıntı ve Simgeler Üzerine

Yazar: Hüseyin Demir

Yıl: 1992-2

Sayı: 7

Ortaöğretim ile ilgili olarak bazı kavram, tanım, bağıntı ve simgeler üzerinde durmak istiyoruz. Bunlardan bir kısmı yıllardır kafamızı kucalamış ve çözüm arayışına girmiştir. Bu doğrultuda matematiğin güzelliğine yaraşır ve bazı önerilerimizi bu yazımızda sunmak istiyoruz. Bu önerilerimizin benimseneceğine de inanıyoruz.

Herhangi bir nokta kümesine şekil dendiğini bilmekteyiz. Önerilerimiz maddeler halinde aşağıda sunulmuştur:

Nokta, doğru ve düzlem

Hilbert’e uyarak noktaları $A$, $B$ gibi büyük harflerle, doğruları $a$, $b$ gibi küçük harflerle ve düzlemleri de $\alpha ,\beta$ gibi küçük Yunan harfleriyle gösterelim. Böyle yapmakla yazılmış bir metni ve çizilmiş bir şekli daha iyi anlamış oluruz.

Noktadaşlık, doğrudaşlık, düzlemdeşlik

Bir doğru üzerinde bulunan noktalara doğrusal noktalar deniliyor. Benzer olarak bir noktadan geçen doğrulara da noktasal doğrular denmesi gerekirse de bunun aynı noktadan geçen doğrular anlamına geldiği pek söylenemez. Bu bakımdan şu anlamlı sözleri benimsiyoruz: Aynı noktadan geçen doğrulara (düzlemlere) noktadaş doğrular (düzlemler), aynı doğru üzerinde bulunan noktalara (düzlemlere) doğrudaş noktalar (düzlemler) ve aynı düzlem üzerinde bulunan nokta ve doğrulara da düzlemdeş noktalar (doğrular) diyoruz.

Açılar, üçgenler ve uzaklıklar

Açılar için $\widehat{AOB}$ simgesi yerine < $AOB$ simgesini, üçgenler için de $\stackrel{\mathrm{△}}{ABC}$ simgesi yerine $\mathrm{△}$ $ABC$ simgesini öneriyoruz. Böyle yapmakla hem sadeliğe gitmiş hem de kitaplarda satır aralıklarını korumuş oluruz.

Ölçülere gelince

m($\widehat{AOB}$) yerine $\sphericalangle$ $AOB$

m($\stackrel{\mathrm{△}}{ABC}$) yerine $|ABC|$

simgelerini benimseyebiliriz.

Ayrıca, bir $P$ noktasının bir $A$ noktasından, bir $a$ doğrusundan ve bir $\alpha$ düzleminden uzaklıklarını sırasıyla

$|PA|,|Pa|,|P\alpha |$

olarak gösterebiliriz.

Orta üçgen, değme üçgeni, ortik üçgen

Bir üçgende kenarların orta noktalarını köşe kabul eden üçgene orta üçgen, iç çemberin kenarlara değdiği noktaları köşe kabul eden üçgene değme üçgeni ve yüksekliklerin kenarlar üzerindeki ayaklarını köşe kabul eden üçgene ortik üçgen adını veriyoruz. Orta üçgen kavramı kolayca çokgenlere ve değme üçgeni kavramı da teğetler çokgenine genelleştirilebilir.

Üçgende dış çemberler ile ilgili olarak değme dış üçgenlerinden söz edilebilir.

Tam üçgen, tam dörtgen

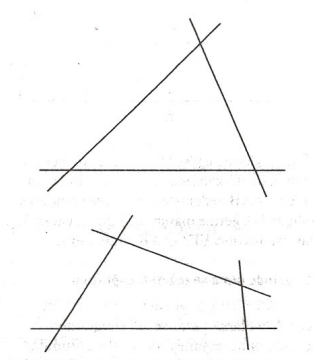
Geometride tam dörtgen kavramı yer almaktadır ve şöyle tanımlanıyor: Herhangi üçü doğrudaş olmayan ve herhangi ikisi kesişen dört doğrunun oluşturduğu bir şekle tam dörtgen denir. Bu ise bir dörtgende kenarlar uzatılarak elde edilen şekildir. Pekiyi neden tam üçgen kavramı geometride yer almasın? bunu da şöyle tanımlarız: Noktadaş olmayan üç doğrunun oluşturduğu bir şekle tam üçgen denir. Bu da bir üçgende kenarların uzatılmasıyla elde edilen şekildir.

Üçgenlerde pek çok teorem aslında tam üçgenlerle ilgilidir. Örneğin dış çemberler, Menelaus ve Ceva teoremleri, gerek açık üçgende ortik üçgen bunlardan birkaçıdır. İlk ve ortaokullarda öğrencilerin geniş açılı bir üçgende yükselikleri çizememeleri, tam üçgen kavramına yer verilmemiş olmasıdır. Sanıyorum tam üçgen verilirse çizimde başarılır olabilirler.

Kiriş kavramı

Çemberlerde tanımlanan kiriş kavramı kolaylıkla çokgenlere, kapalı öteki eğrilere ve hatta şekil çiftlerine genelleştirilebilir.

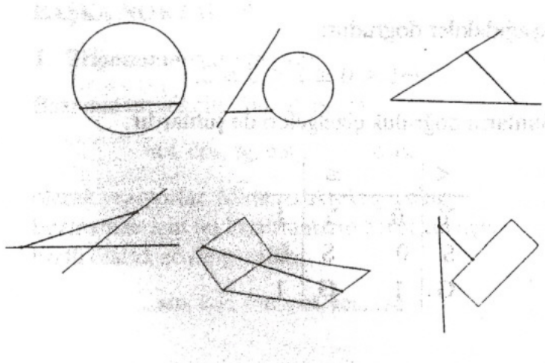
Aşağıda kapalı birkaç şekil ve şekil çiftleri verilmiş ve bunlardan tanımlanabilen kirişler çizilmiştir.

Böylece, bir üçgenin, bir dörtgenin, bir açının bir doğru çiftinin, bir doğru ile bir düzlemin, bir nokta ile bir doğrunun kirişlerinden söz edebiliriz.

Kiriş kavramının böylece genelleştirilmesi ile pek çok teorem ve problem daha kolay olarak ifade edilebilir.

Yamuk kavramı

“Yamuk” sözcüğünün sözlük anlamı, kitaplarda yamuğun şöyle tanımlanmasına yol açıyor: “Sadece karşılıklı iki kenarı birbirine paralel olan bir dörtgene yamuk denir.”

Bu tanım, paralelkenar ve dolayısı ile eşkenar dörtgen, dikdörtgen ve kareyi dışlamaktadır. Oysa yamuktaki, her özellik bu şekillerde geçerlidir, yani bunlarda birer yamuktur. Örneğin yamuğun alan formülü dışlanmış olan bu özel şekillerde geçerli kalmaktadır.

Buna göre yamuğun tanımı şu olmalıdır: “Karşılıklı iki kenarı paralel olan dışbükey bir dörtgene yamuk denir”. Böylece paralelkenar, eşkenar dörtgen, dikdörtgen ve kare birer yamuk olur.

Sanıyorum, aynı durum dikdörtgenlerde de var. Bunun tanımı da kareyi dışlıyor. Gerçekten, ilkokul üçüncü sınıftan bir öğrenciye aşağıdaki soruyu sorduğumda aldığım cevap bunu gösterdi.

Soru: Bir kenarının uzunluğu 4$cm$ ve çevre uzunluğu 16$cm$ olan bir dikdörtgende öteki kenarın uzunluğu kaç $cm$ dir?

Çocuk, zihnen yaptığı hesap sonucundan buna şu cevabı verdi: Böyle bir dikdörtgen olamaz!

Dikdörtgenlerden söz edilirken uzun kenar, kısa kenar terimleri kullanılmamalı. Örneğin şöyle denmeli: Kenar uzunlukları 6 ve 4$cm$ olan bir dikdörtgenin alanı kaç $c{m}^2$ dir?

Yamukta paralel kenarlardan birine taban denirse ötekine üst taban, öteki iki kenara da yan kenarlar ve açılardan tabanlı ilgili olanlara taban açıları deniliyor.

İkizkenar yamuğu tanımlayalım: Taban açıları eş olan bir yamuğa ikizkenar yamuk demir. (Yan kenarları eş olan bir yamuk ikizkenar yamuk olmayabilir. Gerçekten her paralelkenar ikizkenar yamuk değildir.)

Yamukta taban kavramını genişletebiliriz. Yamuğun, tabana paralel olan bir kirişine ara taban denir. Orta taban bunlardan biridir.

Bağıntılar

Paralellik ve eşparalellik

İki doğrunun paralelliği şöyle tanımlanıyor: Düzlemdeş olup kesişmeyen $a$ ve $b$ gibi iki doğruya paralel doğrular denir ve bu bağıntı $a$//$b$ olarak gösterilir.

Bu tanımda a ile b nin çakışması dışlanmaktadır. Bu tanım, çakışma durumunu kapsayacak biçiminde genelleştirilebilir ve bu durumda doğrulara eşparalel doğrular denir ve bağıntı $a$///$b$ olarak gösterilir. O halde tanım şu olur:

$a$///$b$ $\iff$ $a$//$bVa$ = $b$

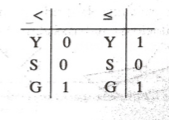
Bu iki bağıntının doğruluk çizelgesi

olup eşparalellik bir denklik bağıntısıdır. (Çizelgede Y yansıma, S simetri, G geçişme özelliğini gösteriyor.)

Sanıyorum, dikkatsiz olunduğunda eğitimde paralellik kavramı eşparalellik anlamında kullanılabilmektedir.

Eşparalellik kavramının kullanılması teorem ve problem ifadelerinin yazılmasında bazı kolaylıklar sağlar. Örneğin öteleme dönüşümü ile ilgili olarak “Bir öteleme, bir doğruyu ya kendisine ya da buna paralel bir doğruya dönüştürür” ifadesi şöyle yazılıverir: “Bir öteleme bir doğruyu buna eşparalel olan bir doğruya dönüştürür”.

İkinci bir örnek olarak bir öğretmenin bir öğrenciye sorduğu şu problemi ele alalım:

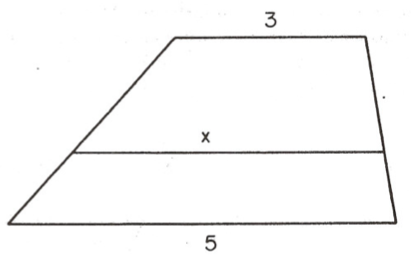
Soru: Şekilde, taban uzunluklar 5 ve 3 birim olan bir yamukta uzunluğu x olan değişken bir $[EF]$ aratabanının alabileceği en büyük değer nedir?

Öğrenci dikkatli değilse “5 tir” cevabını verir ve öğretmen de dikkatsizce bu cevabı kabul eder. Oysa $EF$ // $AB$ nedeniyle x $\ne$ 5 olacağından x uzunluğu 5 değerine ulaşamaz. Eğer cevabın 5 olması isteniyorsa $EF$///$AB$ alınmalıdır.

Üzerinde olma ve teğetlik bağıntıları

Bir $A$ noktası bir $a$ doğrusu üzerinde ise bu ilişkiyi $A/a$ olarak yazar ve “/” simgesine “üzerinde olma bağıntısı” deriz. Bu durumda, $a/A$ da yazar ve bunu “$a$ doğrusu $A$ noktasında geçer” ya da ” $a$ doğrusu $A$ üzerindedir” olarak yorumlarız. Bu açıklamalara göre $A$/$\alpha$, $\alpha$/$A$, $d$/$\alpha$, $\alpha$/$d$ bağıntıları anlam kazanmış olur.

Aynı “/” simgesine teğetlik bağıntısı da der ve $d$/$\mathrm{\Gamma }$ simgesini “$d$ doğrudu $\mathrm{\Gamma }$ çemberine teğettir” olarak yorumlarız.

Sıralama Bağıntısı

Gerçel sayılar için tanımlı ve eşitliği içeren “$S$” bağıntısına cebirciler sıralama bağıntısı ya da eşitlik bağıntısı diyorlar.

$a$ $\le$ $b$ $\iff$ $a<b$ V $a=b$

olup “$<$” bağıntısını da öz sıralama bağıntısı ya da öz eşitsizlik bağıntısı diyebiliriz.

Aşağıdakiler doğrudur:

-1 $<$ 0 $\le$ 1 $<$ 3 $\le$ 3.

Bunların doğruluk çizelgeleri de şunlardır:

Karmaşık sayılarda sıralama bağıntısının geçersizliğini gösterebiliriz. Gerçekten bağıntının geçerli olduğunu kabul ederek bir çelişkiye varalım:

(0,1 $=$ i sayısı sıfır olmayıp ya i $>$ 0 ya da i $<$ 0 dır. Birinci halde

i $>$ 0 $\Rightarrow i^2$ $>$ 0 $\Rightarrow$ -1 $>$ 0 (yanlış)

İkinci halde

i $<$ 0 $\Rightarrow$ -i $>$ 0 $\Rightarrow (-i{)}^2$ $>$0

$\Rightarrow$ -1 $>$ 0 (yanlış)

O halde karmaşık sayılarda eşitsiz bağıntısı geçersizdir.

Kümelerde kapsanma bağıntısı

Bazı matematikçiler kümelerde kapsanma bağıntısı için “$\subset$” simgesini, bazıları da “$\subseteq$” simgesini benimsiyorlar. Bize göre bu simgeler, gerçel sayılarda tanımlı “$<$” ve “$\le$” simgelerine benzediği ve genelde “$\le ”$ eşitsizlik simgesi kullanıldığı için kümelerde de kapsanma bağıntısı için “$\subseteq$ simgesi kullanılmalıdır.

Ekonomi yarattığı için “$\subset$” simgesini savunanlar var. Peki ekonomi için “$\le$” yerin “$<$” yi kullanıyor muyuz?

“$\subseteq$” bağıntısını benimsenmesi, A kümesinin B nin öz altkümesi olmasını sade biçimde A $\subset$ B olarak yazma kolaylığı sağlar. Özetle

A $\subseteq$ B : A kümesi B nin bir alt kümesidir.

A $\subset$ B : A kümesi B nin bir öz altkümesidir.

Başka Noktalar

Trigonometride altı oran

Bazı matematikçiler bu altı oranı

$sin,cos,tg,cotg,sec,cosec$

olarak yazıyorlar. Matematikteki güzelliği bozmamak için bu kısaltmaların herbirini üçer harfli olarak şöyle yazalım:

$\sin ,\cos ,\tan ,\cot ,\sec ,\csc$

$\mathrm{\infty }$ yerine $+\mathrm{\infty }$, örneğin 5 yerine +5 yazalım mı?

Hayır, yazmayalım.

Sonlu kümelerin niceliği

A sonlu küme ise farklı öğelerinin sayısı n(A) ya da s(A) olarak gösteriliyor. Bence liselerde bunlar yerine $|A|$ simgesi benimsenmelidir. Örneğin

A = {-1,0,$\sqrt{2}$} $\Rightarrow$ $|A|$ = 3

Kümelerde öğeler tekrar etmeli mi yoksa etmemeli mi?

Bu soru kafamızı yıllarca kurcalamıştır. Ülkemizde çağdaş matematiğin benimsendiği 60’lı yıllarda kümelerden öğelerin farklı olacağına parmak basılmıştır. Kuşkularımızı gidermek için bu soruyu yabancı bir analizciye yönelttiğimizde aldığım cevap şu oldu: Neden tekrarlanmasın? İşte o gün bugündür bir kümede öğelerin tekrar edebileceklerini savunur olmuşumdur. Buna göre A = {0,1,1,3} simgesi bir kümedir ve bu kümenin niceliği $|A|$ = 3 tür.

Şu örneği ele alalım:

B = {6,$\sqrt{49+29\sqrt{2}}+\sqrt{49-29\sqrt{2}}$}

Bu bir kümedir. Niceliğini bulmak için iki öğenin eşit olup olmadığı incelenmelidir. İnceleme ise $|B|$ = 1 veriyor. Hem neden öğeleri değişken olan

P = {-2,$x^3$-1,$x^2$-3}

gibi kümelerden söz etmeliyim? Bu değişken kümenin $|P|$ niceliği x in değerlerine göre 1, 2 ya da 3 olur.

Alıştırma 1: P = {-2,$x^3-1$,$x^3-3$} ise

a) $|P|$ = 2 denklemini çiziniz,

b) y = $|P|$ fonksiyonunun grafiğini çiziniz.

Alıştırma 2: Bir DEF üçgenini

a) orta üçgen

b) doğru üçgen

c) ortik üçgen

olarak kabul eden ABC üçgenini çiziniz.

Alıştırma 3: Doğruluk çizelgeleri

olan geometrik ikişer bağıntı bulunuz.

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 2. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Sarper Yurtseven‘e ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.