Yazar: Ali Nesin
Yıl: 1992-1
Sayı: 6
Bu yazıda pokerin matematiğini öğreneceğiz. Poker, dört oyuncuyla ve yediliden asa kadar olan 32 kâğıtla oynanır. Her oyuncuya önce beş kâğıt dağıtılır, sonra her oyuncu elindeki beş kâğıttan istediği kadarını değiştirebilir (isterse hiç değiştirmez). En iyi beş kâğıdı olan kazanır, ve oyun yinelenir. Elbet, “en iyi” sözcüğünün tanımlanması gerekir. Örneğin, beş kâğıt aynı renktense, diyelim hepsi maça (♠), bu “iyi” bir eldir. Aynı renkten beş kâğıda renk adı verilir. Bu yazıdaki amaçlarımızdan biri de pokerde ilk dağıtılan beş kağıdın renk olma olasılığını hesaplamak. Önce ciddi matematik yapacağız.
Bir tanımla başlayalım. Eğer $n$ bir doğal sayıysa, $n!= 1 \times 2 \times … \times n$ sayısına eşittir. Örneğin,
$1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720$’dir. $0!=1$ olarak tanımlanır. Bu ilk bakışta pek doğal gelmeyen tanımın nedenini yazının ortalarında bulabilirsiniz.
Elimizde A, B ve C harfleri var, ve bu harflerden iki değişik harfli sözcük yapmak istiyoruz. Kaç sözcük yapabiliriz? Bu soruyu yanıtlamak için sözcükleri -abece sırasına göre- sıralayalım.
AB,AC,BC,BA,CA,CB
Bu sözcüklerin oluşumunu şöyle de gösterebiliriz:
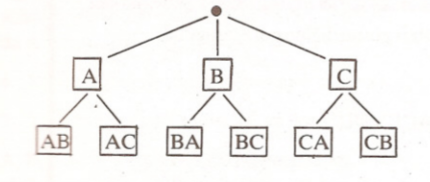
Önce ilk harfleri koyuyoruz: A, B ve C. Sonra ikinci harfleri: eğer ilk harfimiz A ise, ikinci harf için iki seçenek var: B ve C. Dolayısıyla A budağına iki dal ekliyoruz: B ve C dallarını. Demek ki toplam $3\times2=6$ sözcük yazabiliriz.
Şimdi bu soruyu genelleştirelim. Elimizde $n$ değişik harf var:
A$_1$, A$_2$, … A$_n$
ve bu $n$ harften, $r$ değişik harfli sözcükler üretmek istiyoruz (yani her harfi en çok bir kez kullanabiliriz). Kaç sözcük üretebiliriz?
Yukarıdaki gibi ters dönmüş bir ağaç yapalım. Ağacın ilk budağından $n$ dal çıkar: A$_1$ dalı, A$_2$ dalı, … ve A$_n$ dalı. Bunlar sözcüklerin ilk harfleri. Bu dalların ucuna $n-1$ dal gelir (yani ikinci harfler). Örneğin, A$_1$ dalına, A$_2$, …, A$_n$ dalları gelir, ve bu yeni dallar A$_1$A$_2$, …, A$_1$A$_n$ sözcüklerini oluştururlar. Böylece $n\times(n-1)$ dal elde etmiş oluruz. Demek ki $n\times (n-1)$ iki harfli sözcüklerin sayısıdır. Sürdürelim ağacı. Bu $n\times(n-1)$ dala şimdi $n-2$ dal daha ekleyebiliriz. Örneğin, A$_1$A$_2$ dalına, A$_3$, …, $A_n$ dallarını ekleyebiliriz. Bu yeni dalların her birinin ucuna 3 harfli sözcükler yazılır. Böylece $n\times (n-1)\times(n-2)$ tane üç harfli sözcük elde ederiz. Bu yöntemi sürdürsek, A$_1$,…, A$_n$ harflerinden $n\times(n-1)\times…\times(n-(r-1))$ tane $r$ harfli sözcük yazacağımızı görürüz. Bu sayı da $\frac{n!}{(n-r)!}$ sayısında eşittir. İlk teoremimizi kanıtladık:
TEOREM 1: Eğer $r\leq n$ iki doğal sayıysa, A$_1$, … A$_n$ harflerini en çok bir kez kullanarak $$\frac{n!}{(n-r)!}$$ tane sözcük yazılır.
Biraz alıştırma yapalım:
1. SELİM sözcüğünün harfleriyle kaç tane üç harflik sözcük yazabiliriz?
Yukarıdaki teoremi uygulayarak
$\frac{5!}{(5-3)!} = \frac{5!}{2!} =5\times4\times3=60$ sözcük buluruz.
Başka bir soru: SELİM sözcüğünün harfleriyle kaç tane beş harflik sözcük yazılır?
Yine yukarıdaki teoremi uygulayalım:
$\frac{5!}{(5-5)!}= \frac{5!}{0!}$ , ve $0!=1$ eşitliğini kullanarak,
$5!=120$ tane beş harfli sözcük yazabileceğimizi görürüz.
2. MELEK sözcüğünün tüm harflerini kullanarak kaç tane (beş harfli elbet) sözcük yazabiliriz? Yukarıdaki teoremi doğrudan uygulayamayız, çünkü iki E harfi var. Önce iki E’yi ayıralım, ve ME$_1$LE$_2$K “sözcüğünün” tüm harflerini kullanarak kaç tane beş harfli sözcük yazabileceğimizi bulalım. Bu sorunun yanıtı yukarıdaki gibi $5!=120$’dir. Bu sözcüğün $120$ sözcüğün yarısında E$_1$ harfi, E$_2$ harfinden önce gelir; öbür yarısındaysa E$_2$ harfi, E$_1$ harfinden önce gelir. Demek ki, MELEK sözcüğünün tüm harflerinden $120 / 2=60$ sözcük yazabiliriz.
3. Yukarıdaki alıştırmaya benzeyen, ama biraz daha zor olan bir alıştırma daha: KELEBEK sözcüğünün tüm harflerini kullanarak kaç sözcük yazabiliriz?
Yukarıdaki yöntemi kullanalım, ve önce K$_1$E$_1$LE$_2$BE$_3$K$_2$ sözcüğünü ele alalım. Bu sözcükten $7!$ sözcük üretebiliriz. Şimdi, K$_1$=K$_2$ ve E$_1$E$_2$=E$_3$ yapalım. Birinci eşitlik için $2$’ye böleriz, ikinci eşitlik içinse $3!=6$’ya. Demek ki, KELEBEK sözcüğünün harflerinin yerini değiştirerek $\frac{7!}{2}\times 6=420$ sözcük yazabiliriz.
4. A$_1$,A$_2$, A$_3$, A$_4$, A$_5$ sözcüklerinden
$\frac{5!}{(5-3)!}=60$
tane üç harfli sözcük yazabiliriz.
Şimdi yeni bir soru soralım. Elimizde n öğesi olan bir küme var:
$A=\{$A$_1$,…,A$_n\}$.
$r\leq n$, $n$’den küçük bir doğal sayı olsun. $A$ kümesinin kaç tane $r$ öğesi olan altkümesi vardır? Bu sayıyı hesaplayacağız. Bu sayıya (her neyse) $\binom{n}{k}$ adını verelim.
Örnek: $n=5$ ve $r=3$ olsun. $A=\{$A$_1$,A$_2$,A$_3$,A$_4$,A$_5\}$ kümesinin $3$ öğeli alt kümelerini bulalım:
$\{$A$_1$,A$_2$,A$_3\}$
$\{$A$_1$,A$_2$,A$_4\}$
$\{$A$_1$,A$_2$,A$_5\}$
$\{$A$_1$,A$_3$,A$_4\}$
$\{$A$_1$,A$_3$,A$_5\}$
$\{$A$_1$,A$_4$,A$_3\}$
$\{$A$_2$,A$_3$,A$_4\}$
$\{$A$_2$,A$_3$,A$_5\}$
$\{$A$_2$,A$_4$,A$_5\}$
$\{$A$_2$,A$_5$,A$_5\}$
Demek ki $\binom{5}{3}=10$’dur. Bu sayının da $\frac{60}{3!}$ olduğuna dikkatinizi çekerim. Bu rasgele bir eşitlik değildir, ve aşağıda bu eşitliğin nedenini göreceksiniz.
Birinci soruyla arada şu ayrım var: birinci soruda A$_1$A$_2$A$_3$ ve A$_1$A$_3$A$_2$ sözcüklerini ayrı ayrı sayıyorduk. Oysa bu sorumuzda, sözcüklere değil de harflerden oluşan kümelere bakıyoruz. A$_1$A$_2$A$_3$ ve A$_1$A$_1$A$_3$ ve A$_1$A$_3$A$_2$ sözcüklerinin her birinin harflerinden $\{$A$_1$,A$_2$,A$_3\}$ kümesi oluşur. Bunun gibi

Yukarıdaki örnekten yararlanacağız soruyu yanıtlamak için. Birinci teoreme göre, $r$ harfli sözcük sayısı $\frac{n!}{(n-r)!}$’dir. Bu sözcüklerden kaç tanesinin aynı kümeyi verdiğini hesaplayalım. Yine birinci teoreme göre $r$ harfle yazılan $r!$ sözcük olduğuna göre, $\frac{n!}{(n-r)!}$ sözcüklerden $r!$ tanesi aynı kümeyi veriyor. Demek ki
$\binom{n}{r}=\cfrac{\frac{n!}{(n-r)!}}{r!}=$ $\frac{n!}{(n-r)!r!}$
dir.
TEOREM 2: $n$ öğesi olan bir kümenin, $r$ öğelik alt kümelerinin sayısı $$\binom{n}{r}= \frac{n!}{(n-r)!r!}$$ dir.
Bu teoremin kanıtının, $r=3$, $n=5$ için, bir resmini yapalım:
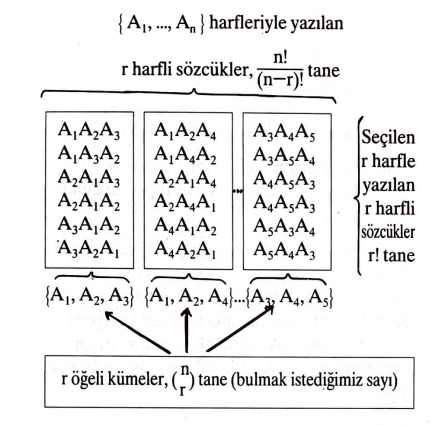
Toplam poker eli sayısı. Şimdi toplam poker eli sayısını hesaplayabiliriz. $32$ kâğıttan kaç tane $5$ kâğıtlık el çıkar? Yani $32$ öğelik bir kümenin kaç tane $5$ öğelik alt kümesi vardır? Teorem 2’ye göre,
$\binom{32}{5}=\frac{32!}{27!5!}=\frac{32\cdot31\cdot30\cdot29\cdot28}{5\cdot4\cdot3\cdot2}=201.376$
tane. yani ikiyüzbinden fazla poker eli vardır.
Renk sayısı. Şimdi de kaç tane “renk” eli olduğunu hesaplayalım. Önce kaç tane maça (♠) eli olduğunu bulalım. Sekiz tane maça var. Bu sekiz maçadan, beş tane seçeceğiz. Teorem 2’ye göre
$\binom{8}{5}=\frac{8!}{3!5!}=\frac{8\cdot7\cdot6}{3\cdot2}=56$
tane salt maça olan el vardır. Toplam dört renk olduğundan (♠,♣,♥,♦), bu sayıyı dörtle çarparsak, toplam renk eli sayısını buluruz:
$56\times4=224$.
Ama bu sayıdan, toplam ‘floş” (aynı renkten ve sürekli kâğıtlar) sayısını çıkarmalıyız. Maçadan floşlar, asla (A, 7, 8, 9, 10), yediliyle, sekizliyle, dokuzluyla ya da onluyla (10, J, Q, K, A) başlayabilir. Demek maçadan beş tane floş var, ve toplam floş sayısı $5 \times 4 =20$. Böylece, gerçek renk sayısı,
$224-20=204$
dür.
Olasılık olarak düşünürsek, elden renk gelme olasılığı
$\frac{204}{201.376} \simeq 0,001013$
dür. Yani aşağı yukarı binde bir.
Kare sayısı, Elden kare gelme, yani beş kâğıttan dördünün aynı sayı olma olasılığını bulalım. Önce dört tane ası olan el sayısını bulalım. Dört tane asın yanına gelebilecek kağıt sayısı $32-4=28$’dir. Demek $28$ tane dört aslı el var. Toplam sekiz tür kâğıt olduğundan,
$28\times8=224$
tane kare el vardır. Bu sayı, renk sayısından biraz daha fazla olduğundan, renk kareyi yener diye düşünebilirsiniz. Nitekim, eğer pokerde kağıt değiştirme olmasaydı, düşündüğünüz gibi olurdu. Ama kâğıt değiştirme olasılıkları da değiştirir. Örneğin, üç ası olan, öbür iki kâğıdını değiştirerek, dört as olma olasılığını arttırır. Bunun gibi eline dört maça gelen, beşinci kâğıdını değiştirerek, renk olasılığını arttırır. Yani poker oyununun sonundaki olasılıklar, ilk beş kâğıdın olasılıklarından değişiktir.
“Ful” sayısı. Eğer bir elde bir türden üç tane, bir başka türden iki tane kâğıt varsa, o ele “ful” denir. Örneğin, üç as ve iki papazdan oluşan bir el fuldür. Elin ful olma olasılığını bulalım. Bu biraz daha zor. Önce elden üç as, iki papaz gelme olasılığını bulalım. Dört astan üçünü seçeceğiz, yani dört öğelik bir kümeden üç öğelik bir küme seçeceğiz. Teorem 2 ‘ye göre
$\binom{4}{3}=4$
seçeneğimiz var aslar için. Şimdi de dört papazdan ikisini seçeceğiz. Yine Teorem 2’ye göre
$\binom{4}{2}=6$
seçeneğimiz var. Demek ki toplam
$4\times6=24$
tane üç as ve iki papazlı el var. Üç papaz ve iki aslı el de $24$ tane. Yani as ve papazlarla
$24+24=48$
tane ful el vardır. Bu hesaplar salt as ve papazlar için değil, tüm iki tür kağıtlar için de geçerli. Örneğin yedililer ve dokuzlularla da $48$ tane ful el vardır. Kaç tane iki tür kağıt var? Toplam sekiz tür var. Bunlardan iki tür seçeceğiz. Teorem 2’ye göre
$\binom{8}{2}=28$
tane iki tür var. Demek ki toplam ful el sayısı
$48\times28=1344$
dür.
“Üç” sayısı. Bir elde üç tane aynı kâğıt varsa, o ele “üç” adı verilir. Ama kare ve fuller üç sayılmaz. Uç sayısını hesaplayalım. Önce üç aslı üç sayısını bulalım. Teorem 2’ye göre
$\binom{4}{3}=4$
çeşit üç as seçebiliriz. Bu üç asın yanına iki kâğıt gelecek, ama herhangi iki kâğıt değil: hiçbiri as olmayacak ve aynı kâğıt olmayacaklar. As dışında $32-4=28$ kâğıt var. Bunlardan iki tane seçelim: $\binom{28}{2}=378$ tane seçenek var. Ama bu seçeneklerden bazıları iki tane aynı tür kağıttan oluşuyor. Bu sayıyı bulup $378$’den çıkartalım. Kaç tane iki papaz seçebiliriz? $\binom{4}{2}=6$ tane. As dışında yedi tür kağıt var.
Demek ki, $378$ seçenekten $6 \times 7 =42$ tanesi iki tane aynı tür kâğıttan oluşuyor. Dolayısıyla, seçilen üç asın yanına,
$378-42=336$
tane iki kâğıtlık el koyabiliriz. Dört tane üç as seçilebildiğinden, aslı üç sayısı $336\times4=1.344$
dür. Bu hesap as dışındaki öbür kağıtlar için de geçerli: yani “üç” el sayısı
$1344\times8 =10.752$
dir.
Öbür olasılık hesaplarını okura alıştırma olarak bırakıyoruz. Yanıtları aşağıdaki dizelgede bulacaksınız. Matematiksel şeytanınız bol olsun.

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Melih Mert Oskay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

