Yazar: Emre Alkan
Yıl: 1992-1
Sayı: 6
Bir $ AB…F$ çokgeninin alanı $|AB…F|$ ile göstereceğiz.
Problem 1: Köşeleri $ A_1,A_2,A_3$ olan üçgenin içteğet çemberi kenarlara sırasıyla $ B_1,B_2,B_3$ te değmektedir. $A_1B_1$ içteğet çemberi $C_1 $ de kessin $C_2 $ ve $ C_3$ te benzer şekilde tanımlansın.
Aşağıdakileri gösteriniz:
i) $ A_1A_2A_3 $ ün alanı $B_1B_2B_3$ ün alanının en az dört katıdır.
ii) $ A_1A_2A_3 $ ün çevresi $ B_1C_2B_3C_1B_2C_3 $ ün çevresi en az $ \sqrt{3} $ katıdır.
iii) $ A_1A_2A_3 $ ün alanı $ B_1C_2B_3C_1B_2C_3 $ ün alanının en az iki katıdır.
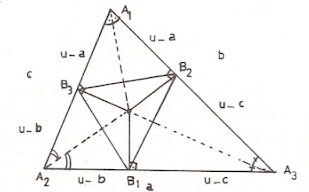
ÇÖZÜM 1: i) $ |A_1A_2A_3| $ $\geq$ $ 4|B_1B_2B_3|$ olduğunu göstermeliyiz.
$ |A_1A_2A_3| $ $=$ $ u \cdot r $, $ A_1A_2A_3 $ ün içteğet çemberi $B_1B_2B_3$ ün çevrel çemberidir.
$B_1B_2$ $=$ $ 2(u-c)$ $ \cdot $ $\sin{\frac{A_3}{2}}$
$B_2B_3$ ve $B_3B_1$ de benzer şekilde yazılarak
$ |B_1B_2B_3|$ $=$ $ \frac{2}{r}$ $(u-a)(u-b)(u-c)$ $\cdot$ $\sin{\frac{A_1}{2}}$ $ \cdot $ $\sin{\frac{A_2}{2}}$ $ \cdot $ $\sin{\frac{A_3}{2}}$
eşitsizliği çıkar.
Sonuç olarak, C. Koç’un yazsındaki (11) ve (16) kullanılırsa istenen
$ |B_1B_2B_3|$ $=$ $ 2|A_1A_2A_3| $ $\sin{\frac{A_1}{2}}$ $\sin{\frac{A_2}{2}}$ $\sin{\frac{A_3}{2}}$ $ \leq$ $\frac{1}{4}$ $|A_1A_2A_3|$
eşitsizliği çıkar.
ii) Şu iki ifadeye bakalım:
* ” $A_1A_2A_3$ eşkenar olduğundan $B_1C_2B_3C_1B_2C_3$ ‘ün çevresi maksimum değerini alır.”
** “İçteğet çemberleri eş olan üçgenler içinde minimum çevreli üçgen eşkenardır.”
* ve ** ‘yi gösterirsek, $A_1A_2A_3$ eşkenar olduğunda bir minimumla bir maksimumu aynı anda yakalamış oluruz. Bu ise derhal problemin ii) ve iii) kısımlarını gösterecektir.
* ‘in ispatı: $B_1C_2B_3C_1B_2C_3$ ‘ün bir düzgün altıgen olması gerektiğini göstereceğiz.
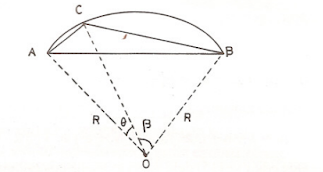
$\widehat{ACB}$ üzerinde bir $C$ bulalım ki $AC+BC$ maksimum olsun.
$AC+BC$ $=$ $2R(\sin\frac{\theta}{2}+\sin\frac{\beta}{2}) $
$R$ ve $ \frac{\theta+\beta}{2}$ sabittir.
$\sin\frac{\theta}{2}+\sin\frac{\beta}{2}$ $=$ $2\sin\frac{\theta+\beta}{4}$ $\cdot$ $\cos\frac{\theta-\beta}{4} $
ancak ve ancak $\theta$ $=$ $\beta$ olduğunda $AC+BC$ maksimum olur. $\mathcal{C}$, $\widehat{ACB}$ yayının orta noktası olmalıdır.
Buradan şu sonucu çıkarabiliriz. Düzgün olmayan bir altıgen çevresi büyütülebilir. Aynı çember içinde maksimum çevreli düzgün altıgendir.
** ise C.Koç’un yazısındaki (15) eştisizliğinin bir yorumundan ibarettir. Şu halde içteğet çemberleri eş üçgenler ailesi içinde minimum çevreli eşkenar üçgendir. $A_1A_2A_3$ eşkenar olduğu zaman
çevre($A_1A_2A_3$)$=$ $\sqrt{3}$ çevre( $B_1C_2B_3C_1B_2C_3$)
olduğu görelebilir.Bu ii)’yi ispatlar. iii) $S$ $=$ $u$ $\cdot$ $r$ olduğundan eş bir içteğet çemberi için minimum alanlı üçgen de eşkenardır. Maksimum alanlı altıgen düzgün olduğu gösterilerek iii) ispatlanır.
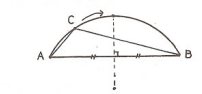
Düzgün altıgenin maksimum alanlı olduğunu görmek için bir yay üzerindeki ortak tabanlı üçgenlerden maksimum alana sahip olanın ikizkenar olduğunu gözlemlemek yeterlidir.
Problem 2. Birinci problemde $B_1C_3$,$B_2C_3$,$B_2C_1$,$B_3C_1$,$B_3C_2$,$B_1C_2$ uzunluklarından en az birinin $12^{-\frac{3}{4}}$,($\frac{abc}{r})^{\frac{1}{2}}$ ifadesinden küçük veya eşit olduğunu gösteriniz.
Çözüm 2: Birinci problemde olduğu gibi $A_1A_2A_3$’ün içteğet çemberini sabit tutalım.$A_1A_2A_3$’ün çevrel çember yarıçapı $R$ olsun.
$|A_1A_2A_3|$ $=$ $\frac{1}{4R}$ $\cdot$ $a$ $\cdot$ $b$ $\cdot$ $c$ $\Rightarrow$ $a$ $\cdot$ $b$ $\cdot$ $c$ $=$ $4R$ $\cdot$ $|A_1A_2A_3|$ elde ederiz. $A_1A_2A_3$ eşkenar olduğundan $|A_1A_2A_3|$ alanının minimum olduğunu 1.problemde bulduk. Euler Teoremine göre $ R \geq 2r =$ sabit ve eşitlik ancak üçgen eşkenarsa vardır. şu halde $A_1A_2A_3$ eşkenarsa $R$’de minimum olmaktadır. Bundan dolayı $a$ $\cdot$ $b$ $\cdot$ $c$ ifadesi üçgen eşkenarsa minimum olur.
Şimdi bunu gösterelim: Bir çember içine çizilen altıgenlerden kenarları çarpımı maksimum olan düzgün altıgendir.
$AC$ $\cdot$ $BC$’in ne zaman maksimum olacağına bakalım
$|ABC|$ $=$ $\frac{1}{2}$ $AC$ $\cdot$ $BC$ $\cdot$ $\sin{\theta}$
yazılabilir. C, $\widehat{ACB}$’nin orta noktası ise $ABC$ alanı maksimum iken $\sin{\theta}$ sabit olduğundan dolayısıyla $AC$ $\cdot$ $BC$’de maksimum olur. Şu halde düzgün altıgenin kenarları çarpımı maksimumdur. Böylece $A_1A_2A_3$ eşkenarken bir maksimum yakaldık. Böylece,
$B_1C_3$,$B_2C_3$,$B_2C_1$,$B_3C_1$,$B_3C_2$,$B_1C_2$ $\leq$ $(a \cdot b \cdot c)^2$ / $3^3$ $4^3 \quad \quad (1)$
elde ederiz. Ceva teoremi yardımıyla
$\frac{u-a}{u-b} \cdot \frac{u-b}{u-c} \cdot \frac{u-c}{u-a}$ $=$ $1$
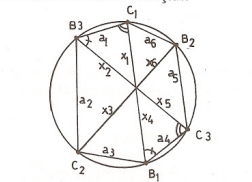
olduğundan $A_1B_1,A_2B_2,A_3B_3$ doğrudan bir noktada kesişirler. Benzerlikten
$\frac{a_1}{a_4} = \frac{x_2}{x_4}$ $\frac{a_3}{a_6} = \frac{x_4}{x_6} $ $\frac{a_5}{a_2} = \frac{x_6}{x_2} $
yazılıp taraf tarafa çarpılırsa
$ a_1 \cdot a_3 \cdot a_5 = a_2 \cdot a_4 \cdot a_6 $ $\Rightarrow$ $B_3C_1 \cdot B_1C_2 \cdot B_2C_3 = B_3C_2 \cdot B_1C_3 \cdot B_2C_1 $ elde edilir.
Altıgenin kenarlarını böylece çarpımları eşit iki kümeye ayırmış olduk. Altıgenin kenarlarından en az biri içteğet çemberinin yarıçapından büyük veya eşit olmalıdır. Genelliği bozmadan $B_3C_1 \geq r$ kabul edelim. (1) eşitsizliğinden, $B_3C_1 \cdot B_1C_2 \cdot B_2C_3 \leq abc/24\sqrt{3}, B_3C_1 \geq r $ olduğu kullanılırsa , $r \cdot B_1C_2 \cdot B_2C_3 \leq abc/24\sqrt{3} $, genelliği bozmadan $B_1C_2 \leq B_2C_3 $ alalım.
$$\Rightarrow (B_1C_2)^2 \leq \frac{abc}{r} \cdot \frac{\sqrt{3}}{72}$$ $$\Rightarrow B_1C_2 \leq 12^{-\frac{3}{4}} \cdot (\frac{abc}{r})^{\frac{1}{2}}$$
elde edilir. Bu da istenen sonuçtur.
Alıştırma: Bir üçgen kenarlar $ a, b, c$ olan alanı da $S$ olsun.
$ a^2+b+c^2 > 6 \cdot S $
olduğunu gösteriniz.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

