Bir Üçgende Noktadaş Dikmeler

Yazar: Hüseyin Demir

Yıl: 1992-1

Sayı: 6

“Noktadaş doğrular” deyince, aynı noktadan geçen doğruları “doğrudaş noktalar” deyince de aynı doğru üzerinde bulunan noktaları anlıyoruz. Buna göre doğrudaş düzlemlerle düzlemdeş şekillerin anlamlarını da vermiş oluyoruz.

Geçen sayıda bir üçgenin kenar doğruları üzerinde bulunan üç noktanın doğrudaş olması için gerek ve yeter koşulu veren Menelaus teoremi ile, bir üçgenin köşelerinden geçen üç doğrunun noktadaş olması için gerek ve yeter koşulu veren Ceva teoremi C. Tezer tarafından ele alınmış ve bu iki teoremin çeşitli uygulamaları verilmişti.

Konuyu tamamalamak için bu yazımızda bir üçgenin kenar doğrularına dik olan üç doğrunun noktadaş olması için gerek ve yeter koşulu veren bir teoremden söz edecek ve bu teoremin birkaç uygulamasına yer vereceğiz.

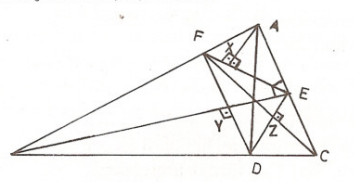
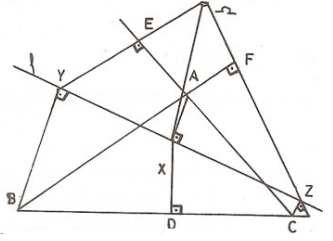
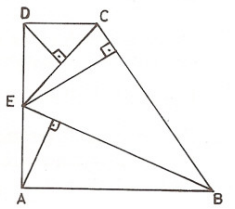
TEOREM: Bir tam üçgen verildiğinde BC, CA, AB kenarlarına D, E, F gibi üç noktada dik olan üç doğrunun noktadaş olması için gerek ve yeter koşul

$|DB{|}^2–|DC{|}^2+|EC{|}^2–|EA{|}^2+|FA{|}^2–|FB{|}^2=0$ (1)

eşitliğidir.

İSPAT: Tam üçgen $ABC$ ve doğrular da $d$, $e$, $f$ olsun.

a) Gereklilik: $d$, $e$, $f$ doğruları bir $P$ noktasında kesişsinler. Bu durumda (1)’deki $u$ toplamı;

Pisagor teoreminden,

$u=|PB{|}^2–|PC{|}^2+|PC{|}^2–|PA{|}^2+|PA{|}^2–|PB{|}^2$

olup sıfırdır.

b) Yeterlilik: (1) eşitliği geçerli olsun. $e$ ve $f$ doğrularının arakesitine $P$ diyelim. $d$ nin $P$ ‘den geçeceğini göstermeliyiz. $P$’den $BC$’ye çizilen $d$ dikmesi $BC$ ‘yi $D$’de kessin. (1) gereğince

$|D^{\prime }B{|}^2–|D^{\prime }C{|}^2+|EC{|}^2–|EA{|}^2+|FA{|}^2–|FB{|}^2=0$ (1′)

olup (1)ve (1′) den

$|D^{\prime }B{|}^2–|D^{\prime }C{|}^2=|DB{|}^2–|DC{|}^2$ (2)

Yönlü uzunlukları (cilt I, Sayı 4, s.15) kullanarak (2) ‘nin her iki tarafını çarpanlara ayıralım:

$(\overline{D^{\prime }B}–\overline{D^{\prime }C})(\overline{D^{\prime }B}+\overline{D^{\prime }C})=(\overline{DB}–\overline{DC})(\overline{DB}+\overline{DC}).$ (3)

Burada

$\overline{D^{\prime }B}–\overline{D^{\prime }C}=\overline{C^{\prime }D}+\overline{D^{\prime }B}=\overline{CB}$

$\overline{DB}–\overline{DC}=\overline{CB}$

olup (3) eşitliği

$\overline{D^{\prime }B}+\overline{D^{\prime }C}=\overline{DB}+\overline{DC}$

‘yi verir. Buradan da

$\overline{D^{\prime }B}–\overline{DB}=\overline{DC}–\overline{D^{\prime }C}$

$⟹\overline{D^{\prime }B}+\overline{BD}=\overline{DC}–\overline{C{D}^{\prime }}$

$⟹\overline{D^{\prime }D}=\overline{D{D}^{\prime }}$

$⟹\overline{D^{\prime }D}=–\overline{D^{\prime }D}⟹\overline{D{D}^{\prime }}=0⟹D^{\prime }=D$

elde olunur. Bu da $d$ ‘nin $P$’ den geçtiğini yani $d$, $e$, $f$ ‘nin noktadaşlığını gösterir.

Bu teoremin en sade iki uygulaması şunlardır.

Uygulama 1. Bir $ABC$ üçgeninde kenarların orta dikmeleri noktadaştır.

Bildiğimiz bu özellik (1) ‘in kullanılmasıyla hemen çözüm bulur:

$(\frac{a}{2}{)}^2–(\frac{a}{2}{)}^2+(\frac{b}{2}{)}^2–(\frac{b}{2}{)}^2+(\frac{c}{2}{)}^2–(\frac{c}{2}{)}^2=0$

Uygulama 2. Bir tam üçgende yükseklikler noktadaştır.

Yüksekliklerin ayakları $D$, $E$, $F$ ise (1) eşitliği, Pisagor teoreminden, hemen gerçekleşir.

(1) ‘deki toplamın $\mathrm{\Sigma }$ ile gösterilmesi.

(1) eşitliği, toplama simgesi olan $\mathrm{\Sigma }$ (sigma) ile şöyle gösterilir:

$\mathrm{\Sigma }(|DB{|}^2–|DC{|}^2)=0$ (4)

Bu yazılışa anlam vermeyenler için sade örneklerle başlayıp açıklama yapalım

1.$a$, $b$, $c$ gibi üç sayı söz konusu olduğunda $\mathrm{\Sigma }a$ toplamını tanımlamak için, $a$, $b$, $c$ sayılarıyla ilgili çembersel permutasyon denilen

$\left(\begin{array}{ccc}a& b& c\\ b& c& a\end{array}\right)$

permutasyonunun uygulanarak $\mathrm{\Sigma }a$ ya şu anlam verilir: $\mathrm{\Sigma }a$ toplamı, ilk terimi $a$, ikinci terimi $a$ nın dönüştüğü $b$ sayısı, son terimide $b$ nin dönüştüğü $c$ sayısının toplamıdır.

$\mathrm{\Sigma }a=a+b+c$

Aynı toplamın $\mathrm{\Sigma }b$ ya da $\mathrm{\Sigma }c$ ile de gösterilebileceği açıktır.

2. Yukarıda verilen kuralla $\mathrm{\Sigma }ab$ toplamı $ab+bc+ca$ ‘dır. Aynı toplam $\mathrm{\Sigma }bc$ ya da $\mathrm{\Sigma }ca$ olarak da gösterilebilir.

3. $\mathrm{\Sigma }(b–c)=b–c+c–a+a+a–b=0$

4. $\mathrm{\Sigma }a(b–c)=\mathrm{\Sigma }ab–\mathrm{\Sigma }ac=\mathrm{\Sigma }ab–\mathrm{\Sigma }ac=0$

5. $\mathrm{\Sigma }bc(b–c)=(b–c)(c–a)(a–b)$ olduğu gösterilebilir. Gösteriniz.

Eğer $a$, $b$, $c$ ve $x$, $y$, $z$ gibi iki grup sayı sözkonusu olursa, çembersel permutasyon her iki gruba ayrı ayrı uygulanır.

6. $\mathrm{\Sigma }a(x–y)=a(x–y)+b(y–z)+c(z–x).$

7. $\mathrm{\Sigma }{a}^2+cy=a^2+cy+b^2+az+c^2+bx.$

$A$, $B$, $C$ ve $D$, $E$, $F$ gibi üçlü iki grup nokta sözkonusu olduğunda da durum aynıdır:

8. $\mathrm{\Sigma }(|DB{|}^2–|DC{|}^2)=|DB{|}^2–|DC{|}^2+|EC{|}^2–|EA{|}^2+|FA{|}^2–|FB{|}^2.$

$a$, $b$, $c$, $d$ gibi dörtlü grup için

9. $\mathrm{\Sigma }ac=ac+bd+ca+db$

eşitliği geçerlidir.

Uygulama 3. bir üçgende iç açıortayların ayaklarından, ilgili kenara çizilen dikmelerin noktadaş olması için gerek ve yeter koşul üçgenin ikizkenar olmasıdır.

İSPAT: Üçgen $ABC$ ve iç açıortaylar $[AD]$, $[BE]$, $[CF]$ ve kenar uzunlukları $a$, $b$, $c$ olsun.

$|DB|={\displaystyle \frac{ac}{b+c}}$ , $|DC|={\displaystyle \frac{ab}{b+c}}$

olup

$\mathrm{\Sigma }(|DB{|}^2–|DC{|}^2)=0$

yazarak $a,b,c$ arasında bir bağıntı elde edelim.

$|DB{|}^2–|DC{|}^2=\frac{a^2{c}^2}{(b+c{)}^2}–\frac{a^2{b}^2}{(b+c{)}^2}$

$=a^2\frac{c-b}{c+b}$ den $\mathrm{\Sigma }{a}^2\frac{c-b}{c+b}=0$

ve paydalardan kurtararak da

$\mathrm{\Sigma }{a}^2(a+b)(a+c)(c-b)=0$

bulunur. $a+b+c=2s$ yazarsak

$a^2(a+b)(a+c)(c-b)$

$=a^2[a^2+(b+c)a+bc](c-b)$

$=a^2[a^2+(2s-a)a+bc](c-b)$

$=2s{a}^3(c-b)+a^{2}bc(c-b)$

eşitliğimiz

$2s\mathrm{\Sigma }{a}^3(c-b)+abc\mathrm{\Sigma }a(c-b)=0$

$\Rightarrow \mathrm{\Sigma }{a}^3(b-c)=0$

olur. Toplamı şöyle çarpanlara ayırırız:

$a^3(b-c)+b^3(c-a)+c^3(a-b)$

$=a^3(b-c)–a(b^3-c^3)+bc(b^2-c^2)$

$=(b-c)[a^3–a(b^2+bc+c^2)+bc(b+c)]$

$=(b-c)[a^3–a{b}^2–abc–a{c}^2+b^{2}c+b{c}^2]$

$=(b-c)[-a(c^2-a^2)+b^2(c-a)+bc(c-a)]$

$=(b-c)(c-a)[-a(c+a)+b^2+bc]$

$=–(b-c)(c-a)(a-b)(a+b+c).$

Bunu da sıfıra eşitlersek ispat bitirilmiş olur.

Uygulama 4. Dar açılı bir üçgende köşelerden ortik üçgenin ilgili kenarlarına çizilen dikmeler noktadaştır.

İSPAT: Üçgen $ABC$ ve ortik üçgen $DEF$ olsun. $A$ ‘nın $EF$, $B$’nin $FD$, $C$’nin de $DE$ üzerindeki dik izdüşümleri $X$, $Y$, $Z$ olsun.

$\stackrel{\mathrm{△}}{DEF}$ üçgeninde

$u=\mathrm{\Sigma }(|XE{|}^2–|XF{|}^2)$

toplamını sıfır olduğunu görmek gerekir:

$u=\mathrm{\Sigma }(|EA{|}^2–|FA{|}^2)$

$=\mathrm{\Sigma }(|DC{|}^2–|DB{|}^2)=0$

Uygulama 5. Tam bir $ABC$ üçgeni ile bunun bir $\ell$ keseni verildiğinde $A$, $B$, $C$ ‘den $\ell$ ‘ye çizilen dikmelerin $X$, $Y$, $Z$ ayaklarından üçgenin karşılıklı kenarlarına çizilen dikmeler noktadaştır (bir $\mathrm{\Omega }$ noktasında kesişirler).

Bu $\mathrm{\Omega }$ (omega) noktasına $\ell$ nin $ABC$ ye göre ortopol’ü deniliyor.

İSPAT: Dikmelerin kenarlar üzerindeki ayakları $D$, $E$, $F$ ise

$\mathrm{\Sigma }(|DB{|}^2–|DC{|}^2)=\mathrm{\Sigma }(|XB{|}^2–|XC{|}^2)$

$=\mathrm{\Sigma }(|BY{|}^2+|YX{|}^2–|CZ{|}^2–|ZX{|}^2)$

$=\mathrm{\Sigma }(|BY{|}^2–|CZ{|}^2)=\mathrm{\Sigma }(|XY{|}^2–|YZ{|}^2)$

$=0+0=0$

Uygulama 6. $A$ ve $D$ açıları dik olan bir yamukta $[AD]$ nin ortası $E$ ise $A$ ‘dan $EB$ ‘ye, $D$ ‘den $EC$ ‘ye ve $E$ ‘den $BC$ ‘ye çizilen dikmeler noktadaşdır.

İspatını kendiniz yapınız!

Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1992 yılı 1. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Muhammet Boran‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.