Yazar: Emre Alkan
Yıl: 1991-5
Sayı: 5
Bu yılki Olimpiyat takımımızın elemanlarından Emre Alkan bir dizi geometri problemini derleyip kendi çözümleriyle beraber Matematik Dünyası’na yolladı. Çözümlerin güzelliği bir yana geçen Sayıda gördüğünüz eşitsizliklerin Aşağıda bu problemlerden bir demet bulacaksınız. Kısa bir açıklama: Bir $ABC$ üçgeninde $h_a, h_b, h _c$ yükseklikleri, $r$ içteğet yarıçapını, $R$ çevrel çemberin yarıçapını, $u = \frac{1}{2}(a + b + c)$ yarıçevreyi ve $S$ alanı gösteriyor.
1. Bir üçgenin yüksekliklerinden en az biri içteğet çemberin yarıçapının üç katından büyük veya eşittir. Gösteriniz.
ÇÖZÜM: Önce $\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}=\frac{1}{r}$ olduğunu gösterelim. Üçgenin alanı için
$$S=\frac{1}{2}ah_a=\frac{1}{2}bh_b=\frac{1}{2}ch_c=ur$$
bağıntılarından:
$$\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}= \frac{a}{2s}+\frac{b}{2s}+\frac{c}{2s}=\frac{2u}{2ur}=\frac{1}{r}$$
Üç pozitif şayının toplamı $1/r$ ye eşitse, en az biri $1/3r$ den küçük eşit olmak zorundadır, yani $h_a, h_b, h_c$ den en az biri $ \geq 3r$ olmalıdır.
- 2. Bir üçgenin içteğet çemberinin kenarlara değdiği noktalardan herbirinin karşısındaki köşe ile birleştirildiğinde oluşan doğru parçalarının uzunlukları $S_a, S_b, S_c$ olsun.
$18S^2 \leq R(s_a + s_b + s_c) ({s_a}^2 + {s_b}^2 + {s_c}^2)$ olduğunu gösteriniz.
ÇÖZÜM: $s_a, s_b$ ve $s_c$yi kullanmak zor olacağından daha kolay uğraşılabilecek uzunluklar bulmalıyız. $h_a \leq s_a, h_b \leq s_b, h_c \leq s_c$ olduğunu gözönüne alırsak,
$$(h_a + h_b + h_c) ({h_a}^2+ {h_b}^2+{h_c}^2) \leq (s_a + s_b + s_c) ({s_a}^2+ {s_b}^2+{s_c}^2)$$
bulunur. Aritmetik-Geometrik Ortalama eşitsizliğine göre,
$$3\sqrt[3]{h_ah_bh_c}\leq h_a + h_b + h_c$$
$$3\sqrt[3]{{h_a}^2{h_b}^2{h_c}^2}\leq {h_a}^2 + {h_b}^2 + {h_c}^2$$
Taraf tarafa çarparsak
$$9h_ah_bh_c \leq (h_a + h_b + h_c)({h_a}^2 + {h_b}^2 + {h_c}^2)$$
Kanıtı tamamlamak için son olarak
$2S^2=Rh_ah_bh_c$ bağıntısını gösterelim. Bunun için
$S=\frac{abc}{4R}$ eşitliğinden yararlanacağız:
$$8S^3 = abch_ah_bh_c =4RSh_ah_bh_c$$
O halde
$$2S^2=Rh_ah_bh_c$$
Eşitlik durumunun ancak eşkenar üçgende olduğunu kolayca görebiliyoruz.
3. Bir üçgenin iç bölgesinde alınan bir $O$ noktasından kenarlara paraleller çiziliyor. Oluşan üçgenlerin alanları $S_1, S_2,S_3$ olsun. büyük üçgenin alam S olmak üzere,
$$(SS_1S_2S_3)^{1/2}\leq S_1S_2 + S_2S_3 + S_3S_1$$ olduğunu gösteriniz.
ÇÖZÜM: Alan ve kenarları şekildeki gibi adlandıralım.
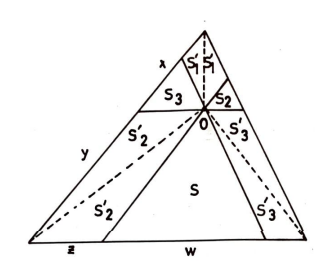
Benzerlikten $\frac{y}{x+y}= \frac{w}{w+z}$, dolayısıyla $\frac{x}{y}= \frac{z}{w}$ buluruz.
Alanlan $S_2^{‘}$ ve $S_3$ olan üçgenlerin yükseklikleri aynıdır; o halde
$\frac{S_3}{S_2^{‘}}=\frac{x}{y}$,
benzer yolla $\frac{S_2^{‘}}{S_1}=\frac{z}{w}$
bulunur. Yukardaki eşitlikten,
$\frac{S_3}{S_2^{‘}}=\frac{S_2^{‘}}{S_1}$,
yani $S_2^{‘}=\sqrt{S_3S_1}$ çıkar.
Diğer üçgenler için de yaparsak
$S_1^{‘}= \sqrt{S_2S_3}, S_3^{‘}=\sqrt{S_1S_2}$ ve
$S=S_1 + S_2 + S_3 + 2S_1^{‘} + 2S_2^{‘} + 2S_3^{‘}=(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3})^2$
elde edilir. Bu durumda göstermek istediğimiz eşitsizlik;
$(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3})\sqrt{S_1}\sqrt{S_2}\sqrt{S_3} \leq S_1S_2 + S_2S_3 + S_3S_1 $ eşitsizliğine dönüşür.
$x, y, z > 0$ için $2xy \leq x^2+ y^2$ eşitsizliğini $z^2$
ile çarpalım; $2xyz^2 \leq x^2z^2+ y^2z^2$. Aynı işlem $y, z$ ve $z, y$ için yapılıp toplanırsa
$(x + y + z)xyz = x^2yz + xy^2z + xyz^2 \leq x^2y^2 + y^2z^2 + z^2x^2$,
$x=\sqrt{S_1}, y=\sqrt{S_2}, z=\sqrt{S_3}$ alınırsa da istenen eşitsizlik gösterilmiş olunur.
Bu problemde eşitlik hali $S_1 = S_2 = S_3$ iken, bunun sonucu olarak da O noktası üçgenin ağırlık merkeziyken vardır.
BAZI TEMEL EŞİTSİZLİKLER: Geçen sayıdaki sorulara yanıtlar:
Albert Erkip
1. Cauchy-Schwarz eşitsizliğini kullanıyoruz:
$d^2 = (2x + 3y)^2 = (2 . x +\frac{3}{2}. 2y)^2 \leq (2^2 + (\frac{3}{2})^2) . (x^2 + 4y^2) = \frac{25}{4}$
O halde $-\frac{5}{2} \leq d \leq \frac{5}{2}$ olmalıdır. Eşitsizliğin eşitlik durumu $x^2+ 4y^2 = 1$ koşulu altında incelenirse $(x, y) = \pm (\frac{4}{5}, \frac{3}{10})$ için $d$ nin $\pm \frac{5}{2}$ değerlerini aldığı görülür, yani maksimum ve minimum $d$ değerleri $\pm \frac{5}{2}$ dir. Problemin geometrik yorumu için $x^2 + 4y^2 = 1$ elipsi ile $2x + 3y = d$ doğrularının konumunu inceleyiniz.
2. $a^kb^k= a … a . b … b \leq (\frac{a+…+a+b+…+b}{k+n})^{k+n} = (\frac{ka+nb}{k+n})^{k+n}$ Burada Aritmetik-Geometrik Ortalama eşitsizliğini kullandık.
3. Cauchy-Schwarz eşitsizliğini iki kere kullanacağız:
$(\sum_{i=1}^{n}a_ib_ic_id_i)^4 = (\sum_{i=1}^{n}(a_ib_i)(c_id_i))^2$
$\leq (\sum_{i=1}^{n}{a_i}^2{b_i}^2)^2 (\sum_{i=1}^{n} {c_i}^2{d_i}^2)^2$
$\leq (\sum_{i=1}^{n}{a_i}^4)(\sum_{i=1}^{n}{b_i}^4)(\sum_{i=1}^{n}{c_i}^4)(\sum_{i=1}^{n}{d_i}^4)$
4. Üçüncü problemde $a_i, b_i, c_i, d_i$ yerine $(a_ib_ic_i)^{1/4}, {a_i}^{3/4}, {b_i}^{3/4}, {c_i}^{3/4}$ alalım.
$(\sum_{i=1}^{n}(a_ib_ic_i)^{1/4}{a_i}^{3/4}{b_i}^{3/4}{c_i}^{3/4})^4$
$\leq (\sum_{i=1}^{n}(a_ib_ic_i)(\sum_{i=1}^{n}{a_i}^{3})(\sum_{i=1}^{n}{b_i}^{3})(\sum_{i=1}^{n}{c_i}^{3})$ gerekli sadeleştirmeleri yapınca sonuç çıkacak.
5. $x + y + z = 1$ ve herbiri pozitif olduğundan $x, y, z$ den en az biri $\frac{1}{2}$ den küçük olacaktır. İfade $x, y, z$ ye göre simetrik olduğundan buna $x$
diyebiliriz. yani $x < \frac{1}{2}$
$d = xy + yz + xz – 2xyz = x(y + z) + (1 – 2x)yz$.
Soldaki eşitsizlik $0 < d$ bu durumda hemen görülüyor. Sağ taraf için Aritmetik-Geometrik Ortalama eşitsizliği ile $y + z = 1 – x$ olduğunu kullanırsak;
$d = x(y + z) + (1 – 2x)yz$
$\leq x(y+ z) + (1 – 2x) (\frac{y+z}{z})^2$
$= x(1- x) + (1- 2x) (\frac{1- x}{2})^2$
$= \frac{1}{4} ( 1 + x^2 – 2x^3)$.
Yine Aritmetik-Geometrik Ortalama eşitsizliğini kullanalım;
$x^2 – 2x^3 = x . x . (1 – 2x) \leq$
$(\frac{x + x + 1 – 2x}{3})^3 = \frac{1}{27}$
Birleştirirsek,
$d \leq \frac{1}{4}(1+ \frac{1}{27})= \frac{7}{27}$
bulunur. Burada eşitlik ancak $y=z$ ve
$x = 1 – 2x$, yani $x = y = z = \frac{1}{3}$ durumunda vardır.
6. Orta satıra Cauchy-Schwarz uygulayacağız:
$a^6 = (\sum_{n=1}^{5} n^3x_n)^2$
$= (\sum_{n=1}^{5} (nx_n)^{1/2}.(n^5x_n)^{1/2})^2$
$\leq (\sum_{n=1}^{5} nx_n) (\sum_{n=1}^{5} n^5x_n) = a . a^5 = a^6$
Demek ki eşitlik durumundayız, bu da
$(\sqrt{x_1}, \sqrt{x_1} ), (\sqrt{2x_2}, \sqrt{2^5x_2}), (\sqrt{3x_3}, \sqrt{3^5x_3}), (\sqrt{4x_4}, \sqrt{4^5x_4}) ve (\sqrt{5x_5}, \sqrt{5^5x_5})$ çiftlerinin orantılı olmasını gerektiriyor.
Bu durum için ise $x_n$ lerden en az dördünün sıfır olması gerekiyor. Denklemlerde yerine koyarak tüm $(x_1, x_2, …, x_5)$ çözümlerini bulabiliriz, bunlar:
$(0, 0, 0, 0, 0), a = 0$;
$(1, 0, 0, 0, 0), a = 1$;
$(0, 1, 0, 0, 0), a = 2$;
$(0, 0, 1, 0, 0), a = 3$;
$(0, 0, 0, 1, 0), a = 4$;
$(0, 0, 0, 0, 1), a = 5$.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 5. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren arşiv ekibi üyesi Hasan Kambay‘a ve tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

