Yazar: Nurettin Ergun
Biliyoruz ki $\{1, 2, \ldots, 10\}$ kümesinin 10 elemanı, $\{1, 2, 2^2, 2^3, \ldots, 2^{100}\}$ kümesinin ise 101 elemanı vardır. $\alpha \not = \beta$ olmak üzere $\{\alpha, \beta\}$ kümesi ile $\{\cos n\pi | n \in\mathbb Z^+\}$ kümesinin ise ikişer elemanları vardır. Çünkü birincisi $\{\alpha, \beta\}$ ikincisi ise $\{-1, 1\}$ kümesine eşittir. Buna karşılık $\{\cos 1, \cos 2, \cos 3,\ldots \}, \mathbb Z = \{0, 1, -1, 2, -2, \ldots\}$ ve $\{k + \sqrt{2} : k\in\mathbb Z \}$ kümelerinin üçünün de sonsuz sayıda fakat “aynı sayıda” elemanları vardır. Bu ne demektir? Tüm sayıların kümesi $\mathbb Z^+$ ile, yalnızca tek doğal sayılardan oluşan $\mathbb Z_t^+ = \{1, 3, 5, \ldots\}$ kümesinin “aynı sayıda” elemana sahip olduklarını söylemek ya da herhangi iki gerçel sayı arasında tüm gerçel sayılar eksenindeki kadar gerçel sayı bulunduğunu iddia etmek daha da şaşırtıcı değil midir? Bu ve benzeri savları kavramak ve kanıtlamak için herşeyden önce “aynı sayıda” ya da “farklı sayıda” elemana sahip olmak, sonlu elemanlı olmak kavramlarına matematiksel bir kesinlik kazandırmak gereklidir. $A$ ve $B$ kümelerine, aralarında bire-bir ve örten bir eşleme (ya da fonksiyon) tanımlanabiliyorsa (ya da tanımlanabildiği matematiksel bir kesinlikle kanıtlanabiliyorsa) bunlara denk ya da eş kuvvetli kümeler denir ve bu olgu kısaca $A\cong B$ işareti ile belirtilir.
Örten ve bire-bİr olan ve bileşkeleri tanımlanabilen iki fonksiyonun bileşke fonksiyonu da örten ve bire-bir olduğundan şu önemli ve temel gerçeğe ulaşırız: $A\cong B$ ve $B\cong C$ ise $A\cong C$ olur. Peki sonlu elemanlı olmak ne demektir? Uygun bir $n$ doğal sayısı için $\{ \mathbb Z_n^+ =\{ 1, 2,\ldots, n\}$ kümesi ile eş kuvvette olan bir kümeye sonlu elemanlı aksi halde sonsuz elemanlı denir. Bu yazıda sonsuz elemanlı bazı ünlü kümelerin neden denk oldukları gösterilecektir. Küme, fonksiyon, tümevarım (indüksiyon) ve gerçel sayı kavramları ile “biraz olsun” tanışmış olmak ve kanıtlamalara katılma çabası, anlatılanları kavramak için sanırız yeterli olacaktır.
Önerme 1: $\mathbb Z\cong\mathbb Z^+$ dir.
Bu önermeyi kanıtlamak için $\mathbb Z$ den $\mathbb Z^+$’ya
$$ f(k) = \left\{\begin{array}{ll} 2k + 1 & k\geq 0\, ise \\ -2k – 1 & k< 0\, ise \\ \end{array} \right. $$
ile tanımlanan $f : \mathbb Z \to \mathbb Z^+$ fonksiyonunun birebir ve örten olduğunu görmek yeter. Aşağıdaki şekilde gözlenen bu duruma biçimsel ispat vermeyi okuyucuya bırakıyoruz.
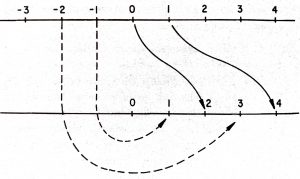
Giriş bölümünde yazılan sonsuz elemanlı üç kümenin denk olduklarını, okuyucu artık kolayca gösterebilecektir. $\cos x = \cos y$ eşitliğinin ancak uygun bir $k \in\mathbb Z$ için $y = x + 2k\pi$ gerçeklenmesi halinde doğru olduğu, dolayısı ile farklı pozitif tam sayılarda farklı kosinüs değerleri alındığı hatırlanmalıdır. Bundan sonraki kanıtlarda okuyucudan daha fazla “katkı” istenecektir.
Önerme 2: Sonsuz elemanlı her küme bir öz alt kümesi ile eş kuvvettedir.
$X$ sonsuz elemanlı olsun. $X – A$ ile $X$ kümesine ait olup da $A$ alt kümesine ait olmayan elemanlar kümesini gösterdiğimizi anımsarsak, adım adım $x_1\in X, x_2\in X_\{x_1\}, x_3\in X_\{x_1, x_2\}, \ldots, x_n\in X_\{x_1, \ldots, x_{n-1}\}, \ldots $ elemanlarını tanımlayabiliriz.
Şimdi $X\cong X – \{x_1, x_2, x_3, \ldots \}$ denkliğinin gerçeklendiğini görmek için
$$ h(n) = \left\{\begin{array}{ll} x_{2n} & x=x_n 0\, ise \\ x & x\notin \{x_1, x_2, \ldots, x_n, \ldots\}\, ise \\ \end{array} \right. $$
biçiminde tanımlanan $h: X\to X – \{x_1, x_3, x_5, \ldots\}$ fonksiyonunun örten ve bire-bir olduğunu gerçeklemek yeterli olacaktır ve bu güç değildir. Sezgisel olarak aşağıdaki şekilden de görebiliriz.
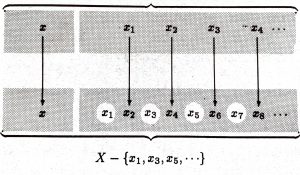
Önerme 3: $a$ ve $b$ gerçel sayıları için $a < b$ gerçeklensin. $\mathbb R \cong (a, b)$’dir.
Evet, herhangi iki gerçel sayı arasında tüm (gerçel) sayı eksenindeki “kadar” gerçel sayı vardır!. Bunu görmek için
$$f(x) = \frac{b – a}{2}\cdot\frac{x}{1 + |x|} + \frac{b + a}{2}$$
şeklinde tanımlanan $f : \mathbb R\to (a, b)$ fonksiyonun bire-bir ve örten olduğu biçimsel bir tamlıkla gösterilebilir ama bunu fonksiyonun aşağıdaki grafiğinden de gözleyebiliriz.
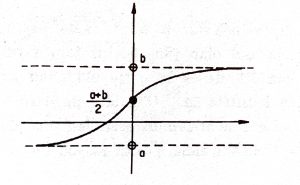
Bu eşleme gibi çeşitli eşlemeler yapılabilir. Netekim, aşağıdaki şekil de $(a, b)$ aralığıyla $\mathbb R$ arasında bire-bir ve örten bir eşleme vermektedir.
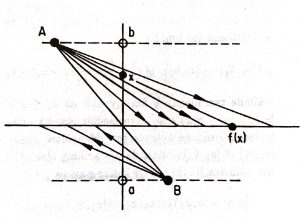
Kanıtlamalara ilgi duyan okuyucunun yukarıda tanımalanan $f$ fonksiyonunun bire-bir olduğunu zorlanmadan gösterebileceğini umuyoruz. Bu fonksiyonun örten olduğu şöyle görülebilir: Herhangi bir $a < x < b$ alındığında $-(b – a) < 2x – (a + b) < b – a$ yani $|2x – (a + b)| < b – a$ ve
$$f\Big(\frac{2x – a(a + b)}{(b – a) |2x – (a + b)|}\Big) = x$$
gerçeklendiği, dolayısı ile $(a, b)$ aralığındaki her gerçel sayının $f$ fonksiyonu altında bir görüntü elemanı olduğu anlaşılır.
Önerme 4: $a < b$ ise $\mathbb R \cong [a, b)$’dir.
$\mathbb R$ gerçel sayılar kümesi ile $[a, b)$ aralığı arasında bire-bir ve örten bir fonksiyonunun varlığını kanıtlamak “biraz daha” çaba gerektirir. Şunları gözleyelim: eğer $X_n(n = 1, 2, \ldots)$ kümeleri kendi aralarında ikişer ikişer ayrık, benzer biçimde $Y_n$ kümeleri de kendi aralarında ikişerli ayrık ve üstelik herbir $n$ için $X_n \cong Y_n$ ise $\cup_{n=1}^\infty X_n \cong \cup_{n =1}^\infty Y_n$ olur, çünkü $h_n: X_n \to Y_n$ örten ve birebir fonksiyonları sayesinde
$$h: \cup_{n=1}^\infty X_n \to \cup_{n=1}^\infty Y_n;$$
$$h(x) = h_m(x) (x\in X_m\,\,\text{ ise})$$
şeklinde tanımlanan $h$ parçalı fonksiyonu, kolayca görülebileceği gibi hem örten hem de bire-birdir.
Dikkat edilirse $\cup_{n=1}^\infty X_n$ birleşim kümesinin herbir elemanı, bir ve yalnız bir $X_n$ kümesine ait olabileceğinden, parçalı $h$ fonksiyonunun tanımında bir ‘belirsizlik’ yoktur. Ayrıca $a_1 < b_1$ ve $a_2 < b_2$ ise, yine $c_1 = \frac{1}{2}(a_1 + b_1)$ ve $c_2 = \frac{1}{2}(a_2 + b_2)$ orta noktalarının yardımı ile
$$g: [a_1, b_1) \to [a_2, b_2);\,\, g(x) = \frac{b_2 – a_2}{b_1 – a_1}(x – c_1) + c_2$$
şeklinde tanımlanan $g$ fonksiyonun da $a_1 \le x < b_1$ için $a_2 \le g(x) < b_2$ gerçeklediği, üstelik örten ve bire-bir olduğu kolayca gerçeklenebileceğinden $[a_1, b_1)\cong [a_2, b_2)$ iddiası da gösterilmiş olur. Geriye yalnızca bu iki bilgiyi kullanmak ve
$$[a, b) = [a, x_1) \cup [x_1, x_2) \cup [x_2, x_3) \cup \cdots,$$
$$\mathbb R = [0, 1) \cup [-1, 0) \cup [1, 2)\ cup [-2, -1) \cup \cdots $$
yazılışlarının geçerliliğini gözlemek kalacaktır. Burada herbir $n$ doğal sayısı için $x_n = b – (b – a)/2^n$ alınmıştır. $x_n\in (a, b)$ gerçel sayılarının artarak $b$ sayısına istenildiği kadar yaklaştığı gözlenmelidir.
Önerme 5: $\mathbb Z^+ \times \mathbb Z^+ \cong \mathbb Q$’dır.
Pozitif tam sayı ikililerinin kümesi olan $\mathbb Z^+ \times \mathbb Z^+$ kümesinden $\mathbb Z^+$ pozitif tam sayılar kümesine büyük usta Cantor’un ünlü köşegen sayma fonksiyonunu tanımlayalım:
$$\forall (n, m)\in \mathbb Z^+ \times \mathbb Z^+$$
için
$$h(n, m) = n + \frac{1}{2}(n + m – 2)(n + m -1).$$
Dikkat edilirse $(n + m -2)(n + m -1)$ negatif olmayan tam sayısı, iki ardışık tam sayının çarpımı olduğundan daima çifttir. O halde herbir $(n, m)$ pozitif tam sayı ikilisi için $h(n, m)$ bir pozitif tam sayıdır. Şunları gözleyelim: Eğer $n+m\le n^* + m^*$ ise $h(n, m)\le h(n^*, m^*)$ olur, çünkü dikkat edilirse, $n + m\le n^* + m^* -1$ ve sonuçta
$$\begin{eqnarray*}h(n,m)&\le&(n + m -1) +\frac{1}{2}(n + m -2)(n + m -1)\\ &=&\frac{1}{2}(n+m)(n+m-2)\\&\le& \frac{1}{2}(n^* + m^* -2)(n^* + m^* -1)\\&<&h(n^*, m^*)\end{eqnarray*}$$ geçerli olacaktır. O halde $h(n, m)= h(n^*, m^*)$ ise zorunlu olarak önce $n + m =n^* + m^*$ ve dolayısı ile sonra
$$\begin{eqnarray*} n &=& h(n, m) – \frac{1}{2}(n+m-1)(n+m-2)\\ &=& h(n^*, m^*) -\frac{1}{2}(n^* + m^* -1)(n^* + m^* -2)\\ &=& n^*\end{eqnarray*}$$
ve sonuçta $(n, m) =(n^* , m^*)$ eşitlikleri geçerli olacaktır. Neden? Demek ki $h$ bire-bir bir fonksiyondur. $h$ üstelik örten bir fonksiyondur, çünkü herbir $N$ pozitif tam sayısı, tek türlü belirli bir $n$ doğal sayısı sayesinde
$$\frac{n(n+1)}{2}, \frac{n(n+1)}{2}+1, \ldots, \frac{n(n+1)}{2}+n$$
pozitif tam sayılarından birisine eşittir; bu sav okuyucu tarafından $N$ sayıları üzerinden tümevarımla kolayca gösterilebilir.
$$\frac{n(n+1)}{2} = h(n, 1)$$
ve $0 < m \le n$ ise
$$\frac{n(n+1)}{2} + m = h(m, n-m+2)$$
olduğundan her $N$ doğal sayısının köşegen sayma fonksiyonunda bir görüntü elemanı olduğu anlaşılır. $h$ fonksiyonunun doğal sayı ikililerini aşağıdaki köşegenler üzerinden saydığına yani
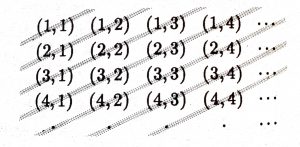
$h(1, 1)= 1, h(1, 2)=2, h(2, 1)= 3,$ vb. gerçeklendiğine dikkat edilmelidir.
Şimdi, verilen bir $n$ pozitif tam sayısı ile aralarında asal olan tüm pozitif tam sayıların kümesinin $\mathbb Z^+$ ile eş kuvvette olduğunu ispatlamadan hatırlatalım. O halde, paydasında $n$ payında ise $n$ ile aralarında asal olan tüm pozitif tam sayıların yer aldığı pozitif rasyonel sayıların kümesi $\mathbb Q^+_n$ (örneğin $\frac{6}{51}\notin \mathbb Q_{51}^+, \frac{2}{17}\in\mathbb Q_{17}^+$ dir) ile, ikinci bileşeni $n$ olan bütün pozitif tam sayı ikililerinin kümesi $\mathbb Z^+\times \{n\}$ için kolayca $\mathbb Q_n^+\cong\mathbb Z^+ \cong \mathbb Z^+\times \{n\}$ bulunur. Sonuçta, tüm pozitif rasyonel sayıların kümesi $\mathbb Q^+$ için
$$\mathbb Q^+ = \bigcup_{n=1}^\infty \cong\bigcup_{n=1}^\infty (\mathbb Z^+\times \{n\}) = \mathbb Z^+\times \mathbb Z^+\cong \mathbb Z^+$$olur, neden? Tüm negatif rasyonel sayıların kümesi $\mathbb Q^-$ için elbette $\mathbb Q^- \cong \mathbb Q^+\cong \mathbb Z^+$ olur. O halde $\mathbb Q^+$ ve $\mathbb Q^-$ kümelerİ doğal sayılarla “numaralandırılır” yani $\mathbb Q^+ = \{r_1^+, r_2^+,\ldots\}$ ve $\mathbb Q^- = \{p_1^-, p_2^-,\ldots\}$ olur ve sonuçta tüm rasyonel sayıların kümesi $\mathbb Q$ için $\mathbb Q = \{0, r_1^+, p_1^-, r_2^+, p_2^-\ldots\}\cong \mathbb Z^+$ elde edilir. Nasıl?
Önerme 6: $\mathbb R\times\mathbb R\cong \mathbb R$’dir.
İşte şaşırtıcı bir başka gerçek daha! Öklid düzlemindeki gerçel sayı ikilileri, tastamam gerçel sayılar eksenindeki gerçel sayılar kadardır. Bunu göstermek, öncekilere göre biraz daha fazla bilgi ve hazırlık gerektirecektir. Öncelikle şuna dikkat edelim: $X_1\cong Y_1$ ve $X_2\cong Y_2$ ise bu denklikleri veren sırasıyla $h_1$ ve $h_2$ örten ve bire-bir fonksiyonları sayesinde, $h(x_1, x_2) =(h_1(x_1), h_2(x_2))$ şeklinde tanımlanan $h$ fonksiyonu yardımı ile $X_1\times X_2 \cong Y_1 \times Y_2$ gerçeklendiğini gözlemek güç değildir. O halde bu önermeyi kanıtlamak için $[0, 1) \times [0, 1)\cong [0, 1)$ göstermek yeterli olacaktır. Neden? Bu sonuncusunu gösterebilmek için önce $[0, 1)$’deki $x$ gerçel sayısının sonsuz ondalık yazılımla
$$x = 0, x_1x_2\cdots x_n\cdots ; x_i\in\{0, 1, \ldots, 9\}$$
biçiminde tek türlü yazılabileceğini anımsayalım. (Bkz. Matematik Dünyası, Cilt I, Sayı 2, s.2). Üstelik belirli bir basamaktan sonra tüm $x_i$’lerin 9 olmadığını varsayabiliriz. Tersine basamakları $0, 1,\ldots, 9$ sayılarından ya da bunların bazılarından oluşan fakat belirli bir yerden sonra bu basamakların hep 9 olmadığı böyle bir “ondalık açılım”,
$$\sum_{n=1}^\infty\frac{9}{10^n}$$
toplamından kesin küçük kalan ve negatif olmayan yani $[0, 1)$ aralığına ait olan bir gerçel sayıdır. Neden? Belirli bir basamaktan sonra tüm diğerlerinin 9 olmasının sakıncası, iki farklı ondalık açılıma sahip olmaktır. Şu örneğe bakın:
$$\begin{eqnarray*}0, 31999\cdots &=& \frac{3}{10} +\frac{1}{10^2} +\frac{9}{10^3} (1 + \frac{1}{10} +\frac{1}{10^2} +\ldots)\\ &=&\frac{3}{10} +\frac{1}{10^2} +\frac{9}{10^3}\cdot\frac{10}{9}\\ &=& 0,32000\cdots \end{eqnarray*}$$
Ayrıca $0,999\cdots = 1\notin [0, 1)$ olduğu gözlenmelidir. Artık Önerme 6’nın kanıtlanabilmesi için, belirli bir basamaktan sonra 9 tekrarlanmaması koşuluna uyan bu ondalık açılımlar yardımı ile
$$h(0,x_1x_2x_3\cdots, 0,y_1y_2y_3\cdots) = 0, x_1y_1x_2y_2\cdots$$
şeklinde tanımlanan $h : [0, 1) \times [0, 1)\to [0, 1)$ fonksiyonunu göz önüne almak yeterlidir.
$h(x, y) = h(x^*, y^*)$ ise eşitliği ve söz konusu koşuldan ötürü basamakların tek türlü belirli olmasının gerekirliği nedeniyle $x_1 = x_1^*, y_1 = y_1^*, \cdots$ ve sonuçta $(x, y) =(x^* , y^*)$ elde edileceği için $h$ bire-birdir. Üstelik $h(0, x_1x_3x_5\cdots, 0,x_2x_4x_6\cdots) = x$ nedeniyle $h$ örtendir. Peki, neden $(a,\infty)\cong \mathbb R\cong [a, b]$ geçerlidir? Eş kuvvette olmayan bazı ünlü küme örnekleri, başka bir yazının konusu olacaktır.
Nurettin Ergun
Biliyoruz ki $\{1, 2, \ldots, 10\}$ kümesinin 10 elemanı, $\{1, 2, 2^2, 2^3, \ldots, 2^{100}\}$ kümesinin ise 101 elemanı vardır. $\alpha \not = \beta$ olmak üzere $\{\alpha, \beta\}$ kümesi ile $\{\cos n\pi | n \in\mathbb Z^+\}$ kümesinin ise ikişer elemanları vardır. Çünkü birincisi $\{\alpha, \beta\}$ ikincisi ise $\{-1, 1\}$ kümesine eşittir. Buna karşılık $\{\cos 1, \cos 2, \cos 3,\ldots \}, \mathbb Z = \{0, 1, -1, 2, -2, \ldots\}$ ve $\{k + \sqrt{2} : k\in\mathbb Z \}$ kümelerinin üçünün de sonsuz sayıda fakat “aynı sayıda” elemanları vardır. Bu ne demektir? Tüm sayıların kümesi $\mathbb Z^+$ ile, yalnızca tek doğal sayılardan oluşan $\mathbb Z_t^+ = \{1, 3, 5, \ldots\}$ kümesinin “aynı sayıda” elemana sahip olduklarını söylemek ya da herhangi iki gerçel sayı arasında tüm gerçel sayılar eksenindeki kadar gerçel sayı bulunduğunu iddia etmek daha da şaşırtıcı değil midir? Bu ve benzeri savları kavramak ve kanıtlamak için herşeyden önce “aynı sayıda” ya da “farklı sayıda” elemana sahip olmak, sonlu elemanlı olmak kavramlarına matematiksel bir kesinlik kazandırmak gereklidir. $A$ ve $B$ kümelerine, aralarında bire-bir ve örten bir eşleme (ya da fonksiyon) tanımlanabiliyorsa (ya da tanımlanabildiği matematiksel bir kesinlikle kanıtlanabiliyorsa) bunlara denk ya da eş kuvvetli kümeler denir ve bu olgu kısaca $A\cong B$ işareti ile belirtilir.
Örten ve bire-bİr olan ve bileşkeleri tanımlanabilen iki fonksiyonun bileşke fonksiyonu da örten ve bire-bir olduğundan şu önemli ve temel gerçeğe ulaşırız: $A\cong B$ ve $B\cong C$ ise $A\cong C$ olur. Peki sonlu elemanlı olmak ne demektir? Uygun bir $n$ doğal sayısı için $\{ \mathbb Z_n^+ =\{ 1, 2,\ldots, n\}$ kümesi ile eş kuvvette olan bir kümeye sonlu elemanlı aksi halde sonsuz elemanlı denir. Bu yazıda sonsuz elemanlı bazı ünlü kümelerin neden denk oldukları gösterilecektir. Küme, fonksiyon, tümevarım (indüksiyon) ve gerçel sayı kavramları ile “biraz olsun” tanışmış olmak ve kanıtlamalara katılma çabası, anlatılanları kavramak için sanırız yeterli olacaktır.
Önerme 1: $\mathbb Z\cong\mathbb Z^+$ dir.
Bu önermeyi kanıtlamak için $\mathbb Z$ den $\mathbb Z^+$’ya
$$ f(k) = \left\{\begin{array}{ll} 2k + 1 & k\geq 0\, ise \\ -2k – 1 & k< 0\, ise \\ \end{array} \right. $$
ile tanımlanan $f : \mathbb Z \to \mathbb Z^+$ fonksiyonunun birebir ve örten olduğunu görmek yeter. Aşağıdaki şekilde gözlenen bu duruma biçimsel ispat vermeyi okuyucuya bırakıyoruz.

Giriş bölümünde yazılan sonsuz elemanlı üç kümenin denk olduklarını, okuyucu artık kolayca gösterebilecektir. $\cos x = \cos y$ eşitliğinin ancak uygun bir $k \in\mathbb Z$ için $y = x + 2k\pi$ gerçeklenmesi halinde doğru olduğu, dolayısı ile farklı pozitif tam sayılarda farklı kosinüs değerleri alındığı hatırlanmalıdır. Bundan sonraki kanıtlarda okuyucudan daha fazla “katkı” istenecektir.
Önerme 2: Sonsuz elemanlı her küme bir öz alt kümesi ile eş kuvvettedir.
$X$ sonsuz elemanlı olsun. $X – A$ ile $X$ kümesine ait olup da $A$ alt kümesine ait olmayan elemanlar kümesini gösterdiğimizi anımsarsak, adım adım $x_1\in X, x_2\in X_\{x_1\}, x_3\in X_\{x_1, x_2\}, \ldots, x_n\in X_\{x_1, \ldots, x_{n-1}\}, \ldots $ elemanlarını tanımlayabiliriz.
Şimdi $X\cong X – \{x_1, x_2, x_3, \ldots \}$ denkliğinin gerçeklendiğini görmek için
$$ h(n) = \left\{\begin{array}{ll} x_{2n} & x=x_n 0\, ise \\ x & x\notin \{x_1, x_2, \ldots, x_n, \ldots\}\, ise \\ \end{array} \right. $$
biçiminde tanımlanan $h: X\to X – \{x_1, x_3, x_5, \ldots\}$ fonksiyonunun örten ve bire-bir olduğunu gerçeklemek yeterli olacaktır ve bu güç değildir. Sezgisel olarak aşağıdaki şekilden de görebiliriz.

Önerme 3: $a$ ve $b$ gerçel sayıları için $a < b$ gerçeklensin. $\mathbb R \cong (a, b)$’dir.
Evet, herhangi iki gerçel sayı arasında tüm (gerçel) sayı eksenindeki “kadar” gerçel sayı vardır!. Bunu görmek için
$$f(x) = \frac{b – a}{2}\cdot\frac{x}{1 + |x|} + \frac{b + a}{2}$$
şeklinde tanımlanan $f : \mathbb R\to (a, b)$ fonksiyonun bire-bir ve örten olduğu biçimsel bir tamlıkla gösterilebilir ama bunu fonksiyonun aşağıdaki grafiğinden de gözleyebiliriz.

Bu eşleme gibi çeşitli eşlemeler yapılabilir. Netekim, aşağıdaki şekil de $(a, b)$ aralığıyla $\mathbb R$ arasında bire-bir ve örten bir eşleme vermektedir.

Kanıtlamalara ilgi duyan okuyucunun yukarıda tanımalanan $f$ fonksiyonunun bire-bir olduğunu zorlanmadan gösterebileceğini umuyoruz. Bu fonksiyonun örten olduğu şöyle görülebilir: Herhangi bir $a < x < b$ alındığında $-(b – a) < 2x – (a + b) < b – a$ yani $|2x – (a + b)| < b – a$ ve
$$f\Big(\frac{2x – a(a + b)}{(b – a) |2x – (a + b)|}\Big) = x$$
gerçeklendiği, dolayısı ile $(a, b)$ aralığındaki her gerçel sayının $f$ fonksiyonu altında bir görüntü elemanı olduğu anlaşılır.
Önerme 4: $a < b$ ise $\mathbb R \cong [a, b)$’dir.
$\mathbb R$ gerçel sayılar kümesi ile $[a, b)$ aralığı arasında bire-bir ve örten bir fonksiyonunun varlığını kanıtlamak “biraz daha” çaba gerektirir. Şunları gözleyelim: eğer $X_n(n = 1, 2, \ldots)$ kümeleri kendi aralarında ikişer ikişer ayrık, benzer biçimde $Y_n$ kümeleri de kendi aralarında ikişerli ayrık ve üstelik herbir $n$ için $X_n \cong Y_n$ ise $\cup_{n=1}^\infty X_n \cong \cup_{n =1}^\infty Y_n$ olur, çünkü $h_n: X_n \to Y_n$ örten ve birebir fonksiyonları sayesinde
$$h: \cup_{n=1}^\infty X_n \to \cup_{n=1}^\infty Y_n;$$
$$h(x) = h_m(x) (x\in X_m\,\,\text{ ise})$$
şeklinde tanımlanan $h$ parçalı fonksiyonu, kolayca görülebileceği gibi hem örten hem de bire-birdir.
Dikkat edilirse $\cup_{n=1}^\infty X_n$ birleşim kümesinin herbir elemanı, bir ve yalnız bir $X_n$ kümesine ait olabileceğinden, parçalı $h$ fonksiyonunun tanımında bir ‘belirsizlik’ yoktur. Ayrıca $a_1 < b_1$ ve $a_2 < b_2$ ise, yine $c_1 = \frac{1}{2}(a_1 + b_1)$ ve $c_2 = \frac{1}{2}(a_2 + b_2)$ orta noktalarının yardımı ile
$$g: [a_1, b_1) \to [a_2, b_2);\,\, g(x) = \frac{b_2 – a_2}{b_1 – a_1}(x – c_1) + c_2$$
şeklinde tanımlanan $g$ fonksiyonun da $a_1 \le x < b_1$ için $a_2 \le g(x) < b_2$ gerçeklediği, üstelik örten ve bire-bir olduğu kolayca gerçeklenebileceğinden $[a_1, b_1)\cong [a_2, b_2)$ iddiası da gösterilmiş olur. Geriye yalnızca bu iki bilgiyi kullanmak ve
$$[a, b) = [a, x_1) \cup [x_1, x_2) \cup [x_2, x_3) \cup \cdots,$$
$$\mathbb R = [0, 1) \cup [-1, 0) \cup [1, 2)\ cup [-2, -1) \cup \cdots $$
yazılışlarının geçerliliğini gözlemek kalacaktır. Burada herbir $n$ doğal sayısı için $x_n = b – (b – a)/2^n$ alınmıştır. $x_n\in (a, b)$ gerçel sayılarının artarak $b$ sayısına istenildiği kadar yaklaştığı gözlenmelidir.
Önerme 5: $\mathbb Z^+ \times \mathbb Z^+ \cong \mathbb Q$’dır.
Pozitif tam sayı ikililerinin kümesi olan $\mathbb Z^+ \times \mathbb Z^+$ kümesinden $\mathbb Z^+$ pozitif tam sayılar kümesine büyük usta Cantor’un ünlü köşegen sayma fonksiyonunu tanımlayalım:
$$\forall (n, m)\in \mathbb Z^+ \times \mathbb Z^+$$
için
$$h(n, m) = n + \frac{1}{2}(n + m – 2)(n + m -1).$$
Dikkat edilirse $(n + m -2)(n + m -1)$ negatif olmayan tam sayısı, iki ardışık tam sayının çarpımı olduğundan daima çifttir. O halde herbir $(n, m)$ pozitif tam sayı ikilisi için $h(n, m)$ bir pozitif tam sayıdır. Şunları gözleyelim: Eğer $n+m\le n^* + m^*$ ise $h(n, m)\le h(n^*, m^*)$ olur, çünkü dikkat edilirse, $n + m\le n^* + m^* -1$ ve sonuçta
$$\begin{eqnarray*}h(n,m)&\le&(n + m -1) +\frac{1}{2}(n + m -2)(n + m -1)\\ &=&\frac{1}{2}(n+m)(n+m-2)\\&\le& \frac{1}{2}(n^* + m^* -2)(n^* + m^* -1)\\&<&h(n^*, m^*)\end{eqnarray*}$$ geçerli olacaktır. O halde $h(n, m)= h(n^*, m^*)$ ise zorunlu olarak önce $n + m =n^* + m^*$ ve dolayısı ile sonra
$$\begin{eqnarray*} n &=& h(n, m) – \frac{1}{2}(n+m-1)(n+m-2)\\ &=& h(n^*, m^*) -\frac{1}{2}(n^* + m^* -1)(n^* + m^* -2)\\ &=& n^*\end{eqnarray*}$$
ve sonuçta $(n, m) =(n^* , m^*)$ eşitlikleri geçerli olacaktır. Neden? Demek ki $h$ bire-bir bir fonksiyondur. $h$ üstelik örten bir fonksiyondur, çünkü herbir $N$ pozitif tam sayısı, tek türlü belirli bir $n$ doğal sayısı sayesinde
$$\frac{n(n+1)}{2}, \frac{n(n+1)}{2}+1, \ldots, \frac{n(n+1)}{2}+n$$
pozitif tam sayılarından birisine eşittir; bu sav okuyucu tarafından $N$ sayıları üzerinden tümevarımla kolayca gösterilebilir.
$$\frac{n(n+1)}{2} = h(n, 1)$$
ve $0 < m \le n$ ise
$$\frac{n(n+1)}{2} + m = h(m, n-m+2)$$
olduğundan her $N$ doğal sayısının köşegen sayma fonksiyonunda bir görüntü elemanı olduğu anlaşılır. $h$ fonksiyonunun doğal sayı ikililerini aşağıdaki köşegenler üzerinden saydığına yani

$h(1, 1)= 1, h(1, 2)=2, h(2, 1)= 3,$ vb. gerçeklendiğine dikkat edilmelidir.
Şimdi, verilen bir $n$ pozitif tam sayısı ile aralarında asal olan tüm pozitif tam sayıların kümesinin $\mathbb Z^+$ ile eş kuvvette olduğunu ispatlamadan hatırlatalım. O halde, paydasında $n$ payında ise $n$ ile aralarında asal olan tüm pozitif tam sayıların yer aldığı pozitif rasyonel sayıların kümesi $\mathbb Q^+_n$ (örneğin $\frac{6}{51}\notin \mathbb Q_{51}^+, \frac{2}{17}\in\mathbb Q_{17}^+$ dir) ile, ikinci bileşeni $n$ olan bütün pozitif tam sayı ikililerinin kümesi $\mathbb Z^+\times \{n\}$ için kolayca $\mathbb Q_n^+\cong\mathbb Z^+ \cong \mathbb Z^+\times \{n\}$ bulunur. Sonuçta, tüm pozitif rasyonel sayıların kümesi $\mathbb Q^+$ için
$$\mathbb Q^+ = \bigcup_{n=1}^\infty \cong\bigcup_{n=1}^\infty (\mathbb Z^+\times \{n\}) = \mathbb Z^+\times \mathbb Z^+\cong \mathbb Z^+$$olur, neden? Tüm negatif rasyonel sayıların kümesi $\mathbb Q^-$ için elbette $\mathbb Q^- \cong \mathbb Q^+\cong \mathbb Z^+$ olur. O halde $\mathbb Q^+$ ve $\mathbb Q^-$ kümelerİ doğal sayılarla “numaralandırılır” yani $\mathbb Q^+ = \{r_1^+, r_2^+,\ldots\}$ ve $\mathbb Q^- = \{p_1^-, p_2^-,\ldots\}$ olur ve sonuçta tüm rasyonel sayıların kümesi $\mathbb Q$ için $\mathbb Q = \{0, r_1^+, p_1^-, r_2^+, p_2^-\ldots\}\cong \mathbb Z^+$ elde edilir. Nasıl?
Önerme 6: $\mathbb R\times\mathbb R\cong \mathbb R$’dir.
İşte şaşırtıcı bir başka gerçek daha! Öklid düzlemindeki gerçel sayı ikilileri, tastamam gerçel sayılar eksenindeki gerçel sayılar kadardır. Bunu göstermek, öncekilere göre biraz daha fazla bilgi ve hazırlık gerektirecektir. Öncelikle şuna dikkat edelim: $X_1\cong Y_1$ ve $X_2\cong Y_2$ ise bu denklikleri veren sırasıyla $h_1$ ve $h_2$ örten ve bire-bir fonksiyonları sayesinde, $h(x_1, x_2) =(h_1(x_1), h_2(x_2))$ şeklinde tanımlanan $h$ fonksiyonu yardımı ile $X_1\times X_2 \cong Y_1 \times Y_2$ gerçeklendiğini gözlemek güç değildir. O halde bu önermeyi kanıtlamak için $[0, 1) \times [0, 1)\cong [0, 1)$ göstermek yeterli olacaktır. Neden? Bu sonuncusunu gösterebilmek için önce $[0, 1)$’deki $x$ gerçel sayısının sonsuz ondalık yazılımla
$$x = 0, x_1x_2\cdots x_n\cdots ; x_i\in\{0, 1, \ldots, 9\}$$
biçiminde tek türlü yazılabileceğini anımsayalım. (Bkz. Matematik Dünyası, Cilt I, Sayı 2, s.2). Üstelik belirli bir basamaktan sonra tüm $x_i$’lerin 9 olmadığını varsayabiliriz. Tersine basamakları $0, 1,\ldots, 9$ sayılarından ya da bunların bazılarından oluşan fakat belirli bir yerden sonra bu basamakların hep 9 olmadığı böyle bir “ondalık açılım”,
$$\sum_{n=1}^\infty\frac{9}{10^n}$$
toplamından kesin küçük kalan ve negatif olmayan yani $[0, 1)$ aralığına ait olan bir gerçel sayıdır. Neden? Belirli bir basamaktan sonra tüm diğerlerinin 9 olmasının sakıncası, iki farklı ondalık açılıma sahip olmaktır. Şu örneğe bakın:
$$\begin{eqnarray*}0, 31999\cdots &=& \frac{3}{10} +\frac{1}{10^2} +\frac{9}{10^3} (1 + \frac{1}{10} +\frac{1}{10^2} +\ldots)\\ &=&\frac{3}{10} +\frac{1}{10^2} +\frac{9}{10^3}\cdot\frac{10}{9}\\ &=& 0,32000\cdots \end{eqnarray*}$$
Ayrıca $0,999\cdots = 1\notin [0, 1)$ olduğu gözlenmelidir. Artık Önerme 6’nın kanıtlanabilmesi için, belirli bir basamaktan sonra 9 tekrarlanmaması koşuluna uyan bu ondalık açılımlar yardımı ile
$$h(0,x_1x_2x_3\cdots, 0,y_1y_2y_3\cdots) = 0, x_1y_1x_2y_2\cdots$$
şeklinde tanımlanan $h : [0, 1) \times [0, 1)\to [0, 1)$ fonksiyonunu göz önüne almak yeterlidir.
$h(x, y) = h(x^*, y^*)$ ise eşitliği ve söz konusu koşuldan ötürü basamakların tek türlü belirli olmasının gerekirliği nedeniyle $x_1 = x_1^*, y_1 = y_1^*, \cdots$ ve sonuçta $(x, y) =(x^* , y^*)$ elde edileceği için $h$ bire-birdir. Üstelik $h(0, x_1x_3x_5\cdots, 0,x_2x_4x_6\cdots) = x$ nedeniyle $h$ örtendir. Peki, neden $(a,\infty)\cong \mathbb R\cong [a, b]$ geçerlidir? Eş kuvvette olmayan bazı ünlü küme örnekleri, başka bir yazının konusu olacaktır.
Not: Bu yazı Matematik Dünyası Dergisi arşivinden siteye eklenmiştir. Yazı ilk olarak derginin 1991 yılı 3. sayısında yer almıştır. Matematik Dünyası arşivi titiz bir çalışma ile çevrim içi platformlarda yeni okuyucularıyla buluşuyor. Bu yazıyı burada okunabilir hale getiren tüm gönüllü arşiv ekibimize teşekkür ediyoruz. Yazıyı PDF olarak okumak için PDF arşivine buradan ulaşabilirsiniz.

