Timur Karaçay
Çağdaş matematiğin tümüyle sonsuzluk kavramından doğduğunu söylemek yanlış olmayacaktır. 20. yy başlarına kadar, matematiği ilkel (elementary) matematik ve yüksek matematik diye ikiye ayırırlardı. İlkel matematik, toplama, çıkarma, bölme işlemleriyle; yani dört işlemle yapılan matematik idi. Yüksek matematik ise, dört işleme ek olarak limit işleminin de kullanılmasıyla yapılan matematik idi. Bugün, bu tür bir sınıflandırma çok yetersiz kalır. Ama, limit işleminin beşinci işlem olarak matematiğe girişi, matematiğin ilgi alanını çok büyütmekle kalmamış, pek çok fiziksel probleme de çözüm getirmiştir. Çağdaş bilim ve teknolojinin ürünleri varlıklarını tamamiyle limit kavramına borçludurlar. Matematikte limit kavramının doğuşu sonsuz kavramının doğuşuna dayanır. Sonsuz büyükler ve sonsuz küçükler diye adlandırılan kavramlar fiziksel olaylarla da ilişkilidir. Bir niceliğin sınırsız olarak büyümesi ya da küçülmesi doğa olaylarında sık karşılaşılan bir olgudur.
Eski çağlarda düşünürler sonsuz kavramını ele almışlardır. Zaten saymayı öğrenen her insan, her doğal sayının bir ardılı olduğunu kolayca sezmekteydi. Başka bir deyişle, sayma eylemi için kullandığı sayma kümesinin (doğal sayılar) en büyük öğesi yoktu. Çünkü en büyük doğal sayı var olsaydı, o sayıya 1 sayısı eklendiğinde daha büyük bir doğal sayı elde edilecekti. Yani bu sayı kümesi her sınırı aşıyor, sonsuza ulaşıyordu. Öyleyse, basit sayma işlemini yapan herkes sonsuzluk kavramıyla ister istemez karşılaşacaktı.
Ne var ki, eski zamanlarda matematiksel bilgiler sonsuzluğu içeren düşünceleri çözüme ulaştıracak düzeye ulaşmamıştı. O nedenle, sonsuzluğu içeren kimi düşünceler birer çatışkı (paradoks) yaratıyordu. Bu çatışkılar arasında ilginç bulacağınız bazılarını bu sayfada açıklamayı sürdüreceğiz.
Zeno Çatışkısı
M.Ö. 490-435 yılları arasında yaşayan Eski Yunan düşünürü Zeno hızlı bir koşucunun bir kaplumbağaya yetişemeyeceği savını ortaya attı. Zeno şöyle diyordu: Koşucu bir \(A\) noktasında, kaplumbağa bir \(B\) noktasında iken yarış başlamış olsun. Bu konumda, aralarında \(|AB|\) uzaklığı vardır. Bu uzaklık sıfıra eşit değildir. Kaplumbağa ne kadar yavaş, koşucu ne kadar hızlı giderse gitsin, koşucu \(B\) noktasına ulaştığında, kaplumbağa bir \(B_1\) noktasına ulaşacaktır. \(A_1 = B\) diyelim.
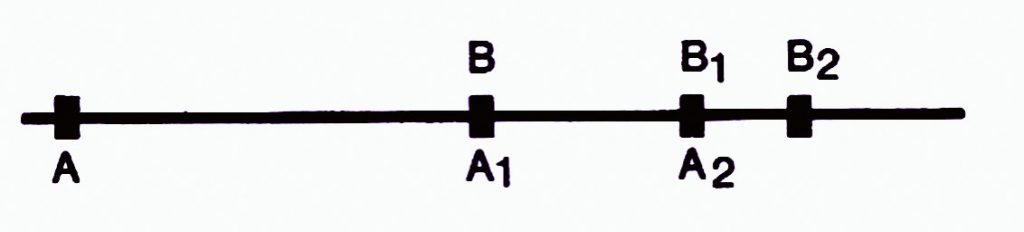
Yeni konumlarıyla, koşucu \(A_1\) kaplumbağa \(B_1\) noktasındadır. Aralarında \(|A_1 B_1|\) uzaklığı vardır. Bu uzaklık da sıfır değildir. Dolayısıyla bu konum ilk konumlarına benzemektedir: Koşucu \(A_1\) noktasından \(B_1\) noktasına erişene dek, kaplumbağa bir \(B_2\) noktasına erişecektir. \(A_2 = B_1\) diyelim. Gene \(|A_2 B_2|\) uzaklığı sıfır olmadığından, bu yeni konumları da ilk konumlarına benzemektedir. Bu olgu \(3., 4., 5., …, n., …\) konumlarda da aynı olacaktır. \(n\) düşünebildiğiniz kadar büyük bir doğal sayı olsun. \(n\) inci konumda, koşucu ile kaplumbağa arasında sıfıra eşit olmayan \(|A_n B_n|\) uzaklığı var olacaktır. Her \(n\) sayısı için benzer konumlar olduğuna göre, koşucu, kaplumbağaya hiçbir zaman yetişemez.
Zeno’nun düşüncesini kavrayabildiğimiz an ona hak veriyoruz; doğru düşündüğünü görüyoruz. Hatta bu çatışkıyı kullanarak hareketen olmadığı sonucuna bile ulaşabiliriz. Zeno’ya göre, atılan bir ok hedefine varamaz. Çünkü hedefe ulaşabilmesi için, önce ilk yarı yolu geçmesi gerekir. İlk yarıyı geçebilmesi için onun da ilk yarısını geçmesi gerekir. İlk yarının yarısını geçebilmesi için onun da ilk yarısını geçebilmesi gerekir… Bu süreç sonsuz olarak yineleceğine göre, atılan ok hedefe ulaşamaz.
Öte yandan, gerçek yaşamda bir koşucunun bir kaplumbağayı geçebileceğini gözlerimizle görüyoruz… Hedefine varamaz diye hiçbirimiz bir okun önüne durmayız…
Zeno’nun ortaya koyduğu mantık ile, gerçek arasındaki bu ayrım yüzyıllar boyunca çözülemeyen bir çatışkı (paradoks) olarak kaldı.
Bunun çözümü için 1000 yıldan fazla bir zamanın geçmesi gerekti. Matematik sonsuz serilerin yakınsaklığı kavramını ortaya koyduktan sonra Zeno’nun çatışkısı kolayca çözüme ulaştı. Şimdi bu kolay çözümü vereceğiz:
Koşucunun \(A\) noktasından \(A_1\) noktasına ulaşması için geçen zaman \(t_0\), \(A_1\) noktasından \(A_2\) noktasına ulaşması için geçen zaman \(t_1\), \(A_2\) noktasından \(A_3\) noktasına ulaşması için geçen zaman \(t_2, …, A_n\) noktasından \(A_{n+1}\) noktasına ulaşması için geçen zaman \(t_n, …\) olsun. Bütün bu zamanların toplamı
\[\sum_{n = 0}^{\infty} t_n\]
olacaktır. Örneğin, kaplumbağanın hızını epeyce abartılı seçelim: Koşucunun aralarında 10 m. uzaklık olduğunu kabul edelim. Bu durumda, her \(n\) için \(t_n = 1/2^{n+1}\) olacaktır. Dolayısıyla,
\[\sum_{n = 0}^{\infty} \frac{1}{2^{n+1}} = 1\]
olacaktır. Yani koşucu 1 saniyede kaplumbağaya yetişecektir. Benzer yöntemle bir okun hedefine varacağını kanıtlayınız.


