Yazar: Cem Tezer
Yıl: 1991-1
Sayı: 1
Bu yazıda, düzlem Euclid geometrisinde, herbirinin diğerleri tarafından yerine getirilmesi güç hatta imkansız görevleri olan üç açı ve açı ölçüsü kavramını ele alacağız.
Önce Euclid düzlemini \(\mathbb{R}^2\) olarak düşünelim ve \(\mathbb{R}^2\)nin \(\mathbb{R}\) üzerindeki vektör uzayı yapısını kullanarak bazı geometri kavramlarını gözden geçirelim. Burada vereceğimiz tanım ve gösterimler eldeki yazıyla ilgili olup, yaygın veya geleneksel oldukları iddia edilmemektedir.
Birbirinden farklı \(A,\, B,\, C\) noktaları verildiğinde eğer
\[ 0 < t < 1\, ve\, A = t B + (1 – t) C \]
olacak şekilde bir \(t \in \mathbb{R}\) varsa, “\(A\), \(B\) ve \(C\) arasındadır” diyoruz. Bunu kısaca \(BAC\) şeklinde gösterelim.
Gene birbirinden farklı \(A,\, B\) noktaları verildiğinde köşesi \(A\)da olan ve \(B\) den geçen yarıdoğru ile \(\mathbb{R}^2\) nin
\[AB = {X \in AB,\, \tilde XAB}\]
altkümesini kastediyoruz. (Bu tanımla \(A \not\in (AB\) olduğunu işaret edelim.)
Köşe noktaları ortak \(\underline{a} = (OA\), \(\underline{b} = (OB\), \(\underline{c} = (OC\) yarıdoğrularını ele alalım. Eğer \(X\), \(Y\) ve \(Z\) arasında kalacak şekilde \(X \in \underline{a}\), \(Y \in \underline{b}\), \(Z \in \underline{c}\) noktaları varsa “\(a\), \(b\) ve \(c\) arasındadır” diyeceğiz.
Şimdi de birkaç basit cebir kavramını açıklayalım: \(\alpha \in \mathbb{R} – \{0\}\) olsun. \(x,\, y \in \mathbb{R}\) için eğer \(x – y = n \alpha\) olacak şekilde bir \(n\) tamsayısı varsa \(x\stackrel{\alpha}{\sim} y\) yazalım. \(“\stackrel{\alpha}{\sim}”\), \(\mathbb{R}\) üzerinde bir denklik bağıntısı olup bu bağıntıya göre \(x\) i içinde bulunduran denklik sınıfını \([x]_{\alpha}\) ile gösterelim. Yani \(x \stackrel{\alpha}{\sim} y\) olması için gerek ve yeter şart \([x]_{\alpha} = [y]_{\alpha}\) dır. \(\stackrel{\alpha}{\sim}\) a göre denklik sınıflarının kümesini \(\mathbb{R} / \alpha\) ile gösterelim.
$$ [x]_{\alpha} + [y]_{\alpha} = [x + y]_{\alpha}$$şeklinde tanımlanan işlem \(\mathbb{R} / \alpha\) üzerinde doğru tanımlanmış olup, \(\mathbb{R} / \alpha\) yı değişmeli bir grup haline getirir. \(\mathbb{R} / \alpha\) ya “\(\alpha\) devirli sayılar grubu” diyeceğiz.
Önce “\(\alpha\)-ana değer fonksiyonu”
\[E_{\alpha}: \mathbb{R} / \alpha \to \left(- \frac{a}{2},\, \frac{a}{2}\right]\]
\(y = E_{\alpha}([x]_{\alpha})\) sayısı \([x]_{\alpha} = [y]_{\alpha}\) ve \(y \in (- \frac{a}{2},\, \frac{a}{2}]\) şartlarını sağlayan biricik sayı olarak belirlenerek tanımlansın.
İkinci olarak “\(\alpha\)-ikiye bölme fonksiyonu”
\[ Y_{\alpha}: \mathbb{R}/2 \alpha \to \mathbb{R}/\alpha\]
\[ Y_{\alpha}([x]_{2\alpha}) = [x/2]_{\alpha} \]
şeklinde tanımlansın.
Son olarak da
\[ARG: \mathbb{R}^2 – {(0,)} \to \mathbb{R} / 2 \pi\]
fonksiyonunun \((x, y) \in \mathbb{R}^2 – \{(0, 0)\}\) deki değerini
\[\cos \theta = \frac{x}{(x^2 + y^2)^{\frac{1}{2}}}~\sin \theta = \frac{y}{(x^2 + y^2)^{\frac{1}{2}}}\]
eşitliğini sağlayan biricik \([\theta]_{2 \pi} \in \mathbb{R} / 2 \pi\) olarak tanımlayalım.
I. Ham Açı:
Ham açı ile sınır noktaları ortak iki yarıdoğrunun teşkil ettiği bir sırasız çifti yahut da kümeyi anlıyoruz. \(\underline{a} = (OA\), \(\underline{b} = (OB\) yarıdoğrularından oluşan ham açıyı \(\{\underline{a},\, \underline{b}\}\) şeklinde gösterebileceğimiz gibi daha geleneksel bir biçimde \(\measuredangle AOB\) şeklinde de gösterebiliriz. \(\measuredangle AOB\) ham açısının ölçüsü (ölçü için de aynı gösterİm kullanılarak)
\[\measuredangle AOB = |E_{2 \pi}(ARG(\vec{OB}) = ARG(\vec{OA}))|\]
şeklinde \([0,\, \pi]\) aralığında bir gerçek sayı olarak tanımlanır.
Tabii, bu soyut sunuş öğrenciye doğrudan uygulanamaz. Sezgiye daha açık olup, geometri öğreniminin çok erken safhalarında ele alınabilecek bir “tanım” olarak şunu teklif edebiliriz: \(\gamma\), \(O\) merkezli ve birim yarıçaplı bir çember olsun. \(\{K\} = \gamma \cap (OA\), \(\{L\} = \gamma \cap (OB\) ise \(\measuredangle AOB\) sayısı \(\gamma\) üzerinde \(K\) noktasını \(L\) noktasına birleştiren en kısa yayın uzunluğudur.
Geometri öğreniminde, öğrencinin ilk karşılaştığı açı kavramı, bizim ham açı adını verdiğimiz açıdır. Geometrinin tarih içindeki tabii gelişmesine sadık her sunuş için bu açı çeşidinin vazgeçilmez olduğuna inanıyoruz. Özellikle, temel karşılaştırma teoremlerinde bu açı önemli bir yere sahiptir. Bunun, belki en esaslı örneği olarak “büyük açı-büyük kenar” teoremi alınabilir:
Teorem: Bir \(ABC\) üçgeninde \(|AC| > |AB|\) olması için gerek ve yeter şart \(\measuredangle ABC > \measuredangle ACB\) olmasıdır.
Temel denklik teoremleri (örneğin \((KAK\), \(AKA\) vb. teoremler) ve temel karşılaştırma teoremlerindeki (mesela büyük açı-büyük kenar teoremi, üçgen eşitsizliği vb.) önemli ve vazgeçilmez yerine rağmen ham açının ileri geometri bahislerinde çok seyrek kullanılmasının sebebi bu açının kötü cebirsel özellikleri olmasıdır.
\[\measuredangle AOB + \measuredangle BOC = \measuredangle AOC\]
yazabilmek için önce \((OB\) nin \((OA\) ve \((OC\) arasında kalmasını istemek zorundayız.
II. Yönlü Açı:
Yönlü açı ile sınır noktaları ortak iki yarıdoğrudan meydana gelen sıralı bir çift anlıyoruz. Sırasıyla \(\underline{a} = (OA\), \(\underline{b} = (OB\) yarıdoğrularından oluşan yönlü açıyı \((\underline{a},\, \underline{b})\) şeklinde, doğrudan bir sıralı çift olarak yazabileceğimiz gibi, daha geleneklere yakın bir şekilde \(\vec{\measuredangle} AOB\) olarak da gösterebiliriz. \(\vec{\measuredangle} AOB\) yönlü açısının ölçüsünü gene aynı gösterimi kullanarak
\[\vec{\measuredangle} AOB = ARG(\vec{OB}) – ARG(\vec{OA})\]
ile tanımlanan \(2 \pi\) devirli sayı olarak tanımlıyoruz. Gene öğrenciye sunuş için şunu teklif edebiliriz: \(\gamma\), \(O\) merkezli birim yarıçaplı bir çember olsun. \(\{K\} = \gamma \cap (OA\), \(\{L\} = \gamma \cap (OB\) ise \(\gamma\) üzerinde \(K\) noktasını, \(L\) noktasına birleştiren ve saatin tersi yönü artı olarak ölçülen muhtelif yayların uzunlukları birbirlerinden ancak \(2 \pi\) nin katları kadar farklı olabilirler. Bu bize \(2 \pi\) devirli bir sayı verir. Bu sayı \(\vec{\measuredangle} AOB\) yönlü açısının ölçüsüdür.
Yönlü açı özellikle trigonometri sahasının vazgeçilmez aletidir. Sinüs ve kosinüs bu açının fonksiyonları olarak görülmelidir. Ayrıca düzlemin önemli izometrilerinden dönmeler de sabit bıraktıkları nokta ve bir yönlü açı ile tarif olunurlar.
Analitik yöntemlerde yönlü açıların önemi bu açıların güzel cebirsel özelliklerine verilmelidir:
\[\vec{\measuredangle} AOB + \vec{\measuredangle} BOC = \vec{\measuredangle} AOC\]
daima doğrudur.
Yönlü ve ham açı ölçüleri arasında
\[\measuredangle AOB = |E_{2 \pi} (\vec{\measuredangle} AOB)|\]
ilişkisi olduğu açıktır.
III. Doğrular Arasındaki Açı:
Bu halde açı herhangi bir \((a,\, b)\) sıralı doğru çiftidir. Doğrular arasındaki açının ölçüsünü \(\measuredangle (a,\, b)\) ile göstererek şu şekilde tanımlayabiliriz: \(a\), \(b\) paralel veya çakışık doğrularsa \(\measuredangle (a,\, b) = 0\), eğer \(\{O\} = a \cap b\) ve \(A \in a – \{O\}\), \(B \in b – \{O\}\) ise
\[\measuredangle (a,\, b) = [E_{2 \pi}(\vec{\measuredangle} AOB)_{\pi}\]
şeklinde \(\pi\)-devirli bir sayıdır. Gene göze hitap eden bir “tanım” verilebilir; Merkezi \(a\) ve \(b\) nin kesiştiği \(D\) noktası olan birim yarıçaplı bir \(\gamma\) çemberini ele alalım. \(a \cap \gamma = \{A_1,\, A_2\}\), \(b \cap \gamma = \{B_1, B_2\}\) olsun. \(\gamma\) üzerinde, saatin tersi yönü artı sayılarak, \(A_1\), \(A_2\) noktalarından herhangi birini \(B_1\), \(B_2\) noktalarından herhangi birine birleştiren muhtelif yayların uzunlukları birbirlerinden ancak \(\pi\) nin katları kadar farlth olabilirler. Bu bize \(\pi\) devirli bir sayı verir. \(a\) ve \(b\) doğruları arasındaki açının ölçüsü budur.
Önce doğrular arasındaki açının cebirsel olarak son derece elverişli olduğunu işaret edelim. Herhangi \(a, b, c\) doğruları için
\[\measuredangle (a,\, b) + \measuredangle (b,\, c) = \measuredangle (a,\, c)\]
daima doğrudur.
Şimdi de “çemberde çevre açı aynı yanı gören merkez açının yarısıdır” şeklinde sloganlaştırılan önemli teoreme bir göz atalım: Burada hangi açı çeşidinin kullanıldığı belli değildir. \(O\) merkezli bir \(\gamma\) çemberi üzerinde \(A\), \(B\) ve \(X\) noktaları alalım (Şekil 1).
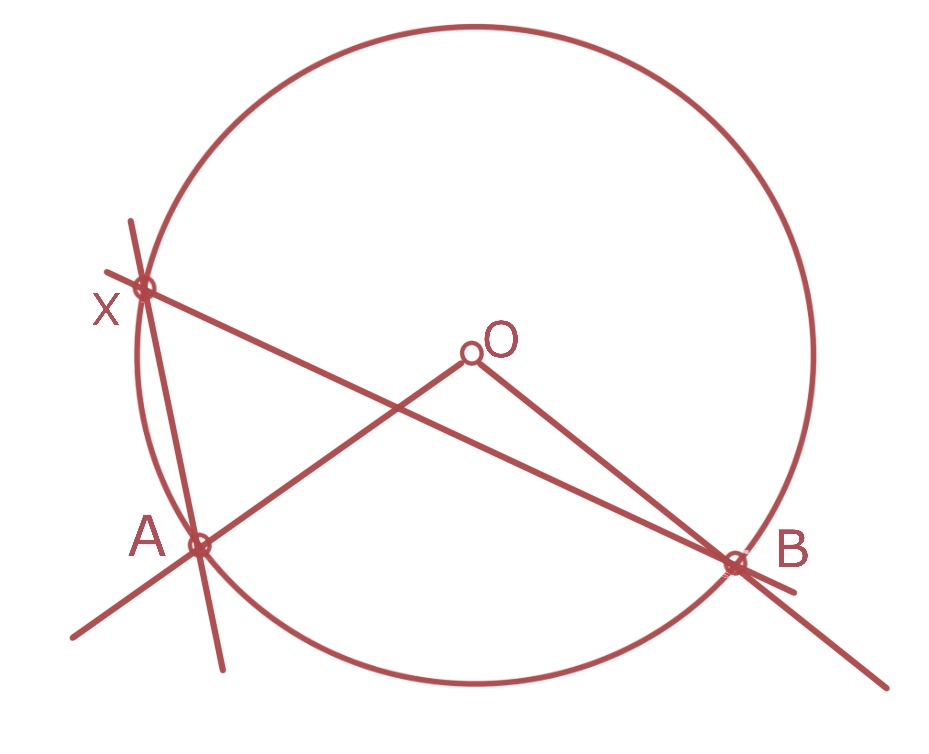
Ham açılar kullanılırsa
\[\measuredangle AXB = \frac{1}{2} \measuredangle AOB\]
söz konusudur. Fakat bu genel olarak yanlış olup ancak \(X\) ve \(O\) noktaları \(AB\) doğrusunun aynı tarafındaysa geçerlidir.
Ham açılar kaldırılıp, yerine yönlü açılar konulduğu takdirde, yani
\[\vec{\measuredangle} AXB = \frac{1}{2} \vec{\measuredangle} AOB\]
söz konusu edildiğinde aynı yanlışlık devam ettikten başka diğer bir pürüz daha ortaya çıkar: \(\vec{\measuredangle} AOB\), \(2 \pi\) devirli bir sayı olduğuna göre, bu miktarın yarısı nasıl anlaşılmalıdır? Gerçekten de \(\mathbb{R} / 2 \pi\) içinde
\[2 x = \vec{\measuredangle} AOB\]
denkleminin aralarında \([\pi]_{2 \pi}\) kadar fark olan tam iki çözümü vardır. \(\vec{\measuredangle} AOB\) nin yarısı olarak bunlardan birini tercih etmek mümkün değildir. Bu zorluk ancak iki farklı açı kavramı bir arada kullanılarak giderilebilir: “Çevre açı” doğrular arasındaki açı, “merkez açı” ise yönlü açı olarak alınmalıdır. Bu durumda \(Y_{2 \pi}: \mathbb{R} / 2 \pi \to \mathbb{R} / \pi\), bu yazının başında tamınlanan ikiye bölme fonksiyonu olmak üzere
\[\measuredangle (X, A, XB) = Y_{2 \pi}(\measuredangle AOB)\]
\(X \neq A,\, B\), olmak kaydıyla \(X\) noktasının yerinden bağımsız olarak doğrudur. (Tabii mesela \(X = A\) hali \(XA\) yerine \(A\) daki teğet alınarak halledilebilir!) Bu gözlem, düzlem geometride yüzlerce konum teoremine esas teşkil eden bir sonuç verir:
Teorem: Birbirinden farklı \(A\), \(B\), \(X\), \(Y\) noktalarının aynı çember veya doğru üzerinde kalmaları için gerek ve yeter şart\[\measuredangle (XA, XB) = \measuredangle (YA, YB)\]
dir.
Bu teoremin kullanılışını, düzlem geometrinin en güzel teoremlerinden birisini ispat ederek örnekleyelim:
Teorem: (Şekil 2) Bir \(ABC\) üçgeninde, \(X \in BC – \{B,\, C\}\), \(Y \in CA – \{C,\, A\}\), \(Z \in AB – \{A,\, B\}\) noktaları verildiğinde, \(AYZ\), \(XBZ\) ve \(XYC\) üçgenlerinin çevrel çemberlerinin ortak bir noktası vardır.
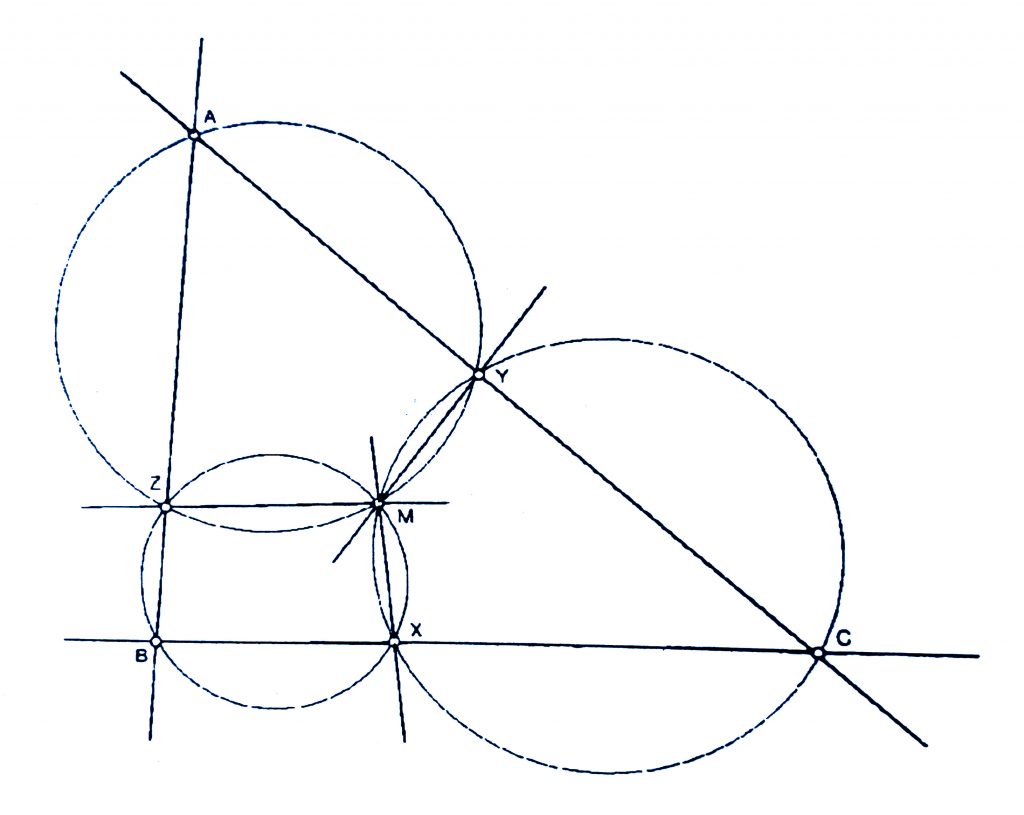
İspat: Sözkonusu üç çemberin hiçbirinin bir diğerine teğet olmadığını varsayalım. \(XYC\) nin çemberi ile \(AYZ\) nin çevrel çemberleri bir \(M = X,\, Y,\, Z\) noktasında kesişirler. \(M\), \(X\), \(C\), \(Y\) bir üzerinde olduğundan
\[\measuredangle (MX,\, MY) = \measuredangle (BX,\, CY) = \measuredangle (BC,\, CA)\]
aynı şekilde \(M\), \(Y\), \(A\), \(Z\) bir çember üzerinde olduğundan
\[\measuredangle (MY,\, MZ) = \measuredangle (AY,\, AZ) = \measuredangle (CA,\, AB\]
ve bu iki eşitlikten de
\[ \measuredangle (MX,\, MZ) = \measuredangle (MX,\, MY) + \measuredangle (MY,\, MZ)\] \[ = \measuredangle (BC,\, CA) + \measuredangle (CA,\, AB)\] \[= \measuredangle (BC,\, AB)\] \[= \measuredangle (BX, BZ)\]bulunur. Demek ki \(B\), \(M\), \(X\), \(Z\) noktaları aynı çember üzerindedir. Sözkonusu çemberlerden ikisinin teğet olması durumunu okuyucuya bırakıyoruz.
Ham ve yönlü açı kavramları yaygınlık kazanmış ve genel olarak doğru anlaşılmışlardır. Buna karşılık, belki de bu ikisinden de önemli olan doğrular arasındaki açı az tanınmış ve sık sık yanlış anlaşılmıştır. “Elemanter” geometri metinlerinde dikkatle kullanılması o kadar yenidir ki Coxeter [1]’de, R.A. Johnson ([4]) ve D.K. Picken’i ([6]) bu açının mucitleri olarak anıyor. H.G. Forder’ın da “cross” dediği ([2]) şey doğrular arasındaki açıdan başkası değil. Aslında kavram ileri geometri metinlerinde (örneğin [5]) daha eskiden kullanılmaktaydı. Gerçekten de Laguerre’in sonlu bir \(O\) noktasında kesişen \(a\) ve \(b\) doğruları arasındaki açıyı \(e^{2 i \theta}\)yı \(a\), \(b\) ve \(O\) dan geçen iki izotropik doğrunun çapraz oranına eşit kılan \(\theta\) olarak tanımlaması geçen yüzyılın ortasına rastlıyor ([3]). Bu \(\pi\) devirli bir miktar olup, bizim verdiğimiz doğrular arasındaki açı ölçüsüne karşılık gelmektedir.
Kaynaklar
- H.S.M. Coxeter: The Real Projective Plane, Cambridge, University Press, 1960.
- H.G. Forder: “The Cross and the foundations of Euclidean geometry” , Mathematical Gazette, 31 (1947) 227-233.
- W.C. Graustein: Introduction to Higher Geometry, Macmillan Company, 1930.
- R.A. Johnson: Modern Geometry, Houghton Mifflin Company 1929.
- F. Klein: Vorlesungen über Nicht-euklidisehe Geometrie, Chelsea Publishing Company, 1926.
- D.K. Picken: “Euclidean geometry of angle” Proceedings of the London Mathematical Society (2), 23 (1925) 45-55.

